Nospareの佐藤 & Nospare・東京大学の菅澤です.
近年,ベイズ分析をする汎用的なツールとしてstanが有名ですが,Rでベイズ分析を行う方法は他にもいくつかありますので,簡単な線形回帰分析に焦点を当てて比較を行なってみようと思います.
Stanとは
マルコフ連鎖モンテカルロ法(MCMC)を使ったベイズ統計的推論や変分法を使った近似ベイズ推定を実行してくれる統計モデリング用のライブラリです.MCMCの中でも特にハミルトニアンモンテカルロ法と呼ばれる汎用的なサンプリング手法が実装されており,ユーザーがモデルや事前分布を記述するだけでベイズ分析を実行することができます.基本的にRとPythonで使用することができます.
比較する方法
- stan (brmsパッケージを経由して使う)
- MCMCpackパッケージ
- フルスクラッチでの実装
brmsはR上でモデルを記述すると自動的にstanコードに変換しstanで実行してくれるパッケージで,線形回帰などの簡易的なモデリングについてはかなり直感的にコーディングが可能です.
使うモデル
以下のような単純な線形回帰を使います.
y_i = \alpha + \beta x_i + \varepsilon_i \qquad \varepsilon_i \sim N(0, \sigma^2), \qquad i=1,\ldots,n.
パラメータの値は$(\alpha, \beta, \sigma)=(2,3,0.6)$とし,サンプルサイズ$n$を5000にして比較をしてみます.
set.seed(123) # 乱数シードの固定
n <- 5000 # サンプルサイズ
e <- rnorm(n, mean = 0, sd = 0.6) # 誤差項
x <- rnorm(n, mean = 0, sd = 1) # 説明変数
y <- 2 + 3 * x + e # 被説明変数
今回は単純な線形回帰モデルを扱っていることとサンプルサイズが十分大きいため,事前分布の細かな違いによる結果の差異は無視できるほど小さいと考えられますので,以下でその点は深く議論しないこととします.
また以下では計算時間なども比較するため,MCMCの長さや収束までのburn-inの長さを統一しておきます.
mc <- 10000 # MCMCの長さ
bn <- 2000 # burn-inの長さ
これは10000個のMCMCサンプルのうち,最初の2000個をburn-in期間として捨てるため,最終的に8000個の事後サンプルが得られることを意味しています.
rstanでの実行(brmsパッケージ経由)
このパッケージは回帰分析向けのStanのパッケージですが,Stanのコードを書く必要がなく,Rの回帰分析ライブラリのlm,glm,lme4と同じような記法でR上に書くだけで,自動的にStanのコードを作ってくれる機能を持っています.また,実際に書かれたStanコードを出力することができ,パラメータの事前分布等を柔軟に設定することができるため,コードを書く時間を大幅に削減することができそうです.
library(brms)
data <- list(N = n, y = y, x = x)
fit.stan <- brm(y ~ x, data = data, iter = mc, warmup = bn, chain=4)
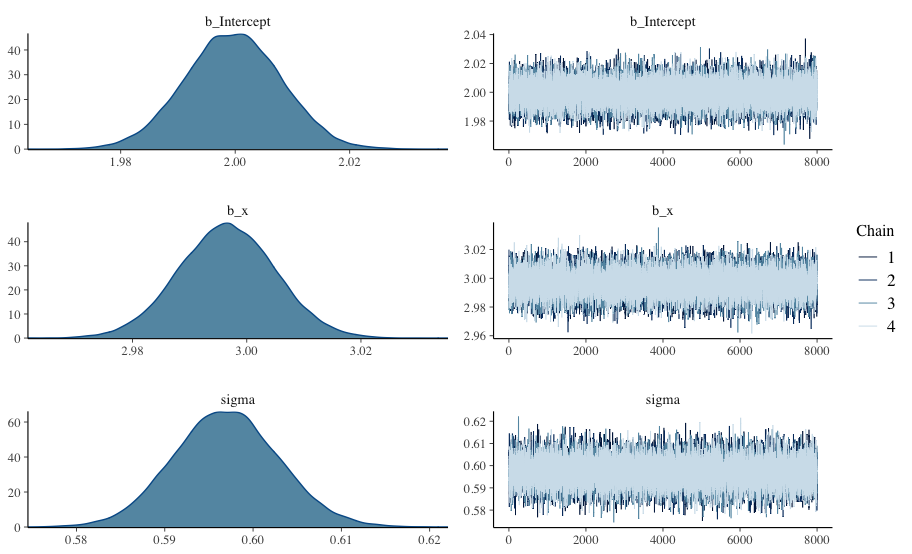
plot(fit.stan)
brm関数の中でchain=4は「異なる初期値から4つのMCMCを回す」ことを意味しています.これにより初期値によってMCMCの挙動が大きく変化しないかをチェックすることができます.Stanでは初めにファイルをコンパイルする時間があり,今回はそれにおおよそ20秒程度かかっていました.ただ,一度コンパイルしたファイルを保存しておくこともできるので,同じモデルをもう一度推定する場合はこの作業は不要ですが,モデルのマイナーチェンジ(説明変数を追加・削除するなど)した場合には再度コンパイルが必要となります.
コンパイル後の実際の計算時間は4つのMCMCで大きく異なることなく,それぞれ約0.7秒程度でした.
生成された事後サンプルは以下のようになりました.
真の値$(\alpha, \beta, \sigma)=(2,3,0.6)$と比べてみると,それぞれ真の値付近に事後分布のマスが集中していることがわかります.
ちなみに,brmにおいて使われているStanコードや事前分布の設定を出力することもできます.
> get_prior(y ~ x, data = data)
prior class coef group resp dpar nlpar bound source
(flat) b default
(flat) b x (vectorized)
student_t(3, 2, 3.1) Intercept default
student_t(3, 0, 3.1) sigma default
この結果から回帰係数の傾きパラメータ$\beta$の事前分布には"flat"とある通り,Stanのデフォルトの事前分布と同様,$(-\infty, \infty)$の一様分布が使われています.
また,切片項$\alpha$,分散$\sigma^2$のパラメータに対してはt分布が使われていることがわかります.
最後にStanコードも出力しておきます.
> make_stancode(y ~ x, data = data)
// generated with brms 2.15.0
functions {
}
data {
int<lower=1> N; // total number of observations
vector[N] Y; // response variable
int<lower=1> K; // number of population-level effects
matrix[N, K] X; // population-level design matrix
int prior_only; // should the likelihood be ignored?
}
transformed data {
int Kc = K - 1;
matrix[N, Kc] Xc; // centered version of X without an intercept
vector[Kc] means_X; // column means of X before centering
for (i in 2:K) {
means_X[i - 1] = mean(X[, i]);
Xc[, i - 1] = X[, i] - means_X[i - 1];
}
}
parameters {
vector[Kc] b; // population-level effects
real Intercept; // temporary intercept for centered predictors
real<lower=0> sigma; // residual SD
}
transformed parameters {
}
model {
// likelihood including constants
if (!prior_only) {
target += normal_id_glm_lpdf(Y | Xc, Intercept, b, sigma);
}
// priors including constants
target += student_t_lpdf(Intercept | 3, 2, 3.1);
target += student_t_lpdf(sigma | 3, 0, 3.1)
- 1 * student_t_lccdf(0 | 3, 0, 3.1);
}
generated quantities {
// actual population-level intercept
real b_Intercept = Intercept - dot_product(means_X, b);
}
このようにbrmによって効率的なStanコードを自動的に生成することができるので非常に便利です.
MCMCpackでの実行
MCMCpackでの線形回帰モデルの推定は,MCMCregressという関数で実行できます.
この関数ではギブスサンプリングによるMCMCの方法が実装されています.
fit.mcmcpack <- MCMCregress(y~x, data=data, burnin = bn, mcmc = mc-bn)
関数MCMCregressの注意として,mcmcの入力値は「burn-in期間後に何個事後サンプルを生成するか」を表した数のため,トータルのMCMCの長さはmcmcとburninの入力値の合計になります.
Stanと同じ長さのMCMCを実行するため,mcmcの入力値をmc-bnとしておきます.
計算時間はおよそ0.17秒程度で,Stanの計算時間よりはかなり短くなっていました.これは線形回帰モデルは単純なギブスサンプリングでMCMCを実行することができ,MCMCregressはその方法を採用しているからだと考えられます.
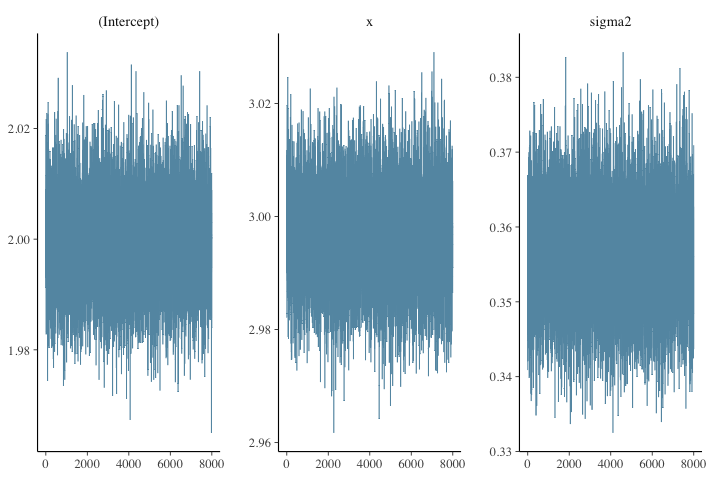
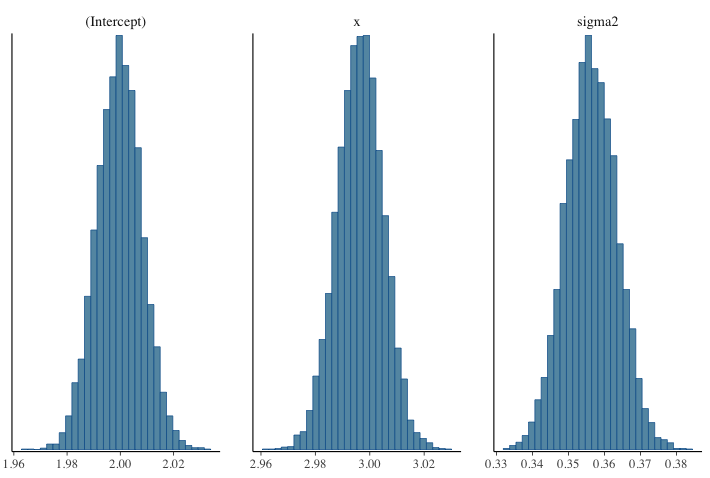
結果を図示してみましょう.
library(bayesplot)
mcmc_trace(fit.mcmcpack)
mcmc_hist(fit.mcmcpack)
上図でsigma2は$\sigma^2$の事後サンプルであることに注意してください.
$\sigma^2$の真値は$(0.6)^2=0.36$なので,それぞれのパラメータの事後分布が真値付近にマスを持っていることがわかります.
また,この結果はStanの結果とほぼ同じになっています.
フルスクラッチでの実装
次にパッケージを使わずにフルスクラッチでギブスサンプリングを実装してみます.回帰係数$\alpha$, $\beta$にはそれぞれ一様分布,$\sigma^2$には$IG(1, 1)$の逆ガンマ分布を用います.
coef.pos <- matrix(NA, mc, 2)
sig.pos <- matrix(NA, mc)
coef <- c(0, 0)
sig <- sd(y)
X <- cbind(rep(1, n), x)
hBeta <- solve(t(X) %*% X) %*% t(X) %*% y
mat <- solve(t(X) %*% X)
for (k in 1:mc) {
coef <- mvrnorm(1, hBeta, sig^2*mat)
res <- y - coef[1] - coef[2]*x
sig <- sqrt( rinvgamma(1, 1 + 0.5*n, 1 + 0.5*sum( res^2 ) ) )
coef.pos[k,] <- coef
sig.pos[k] <- sig
}
coef.pos <- coef.pos[-(1:bn),]
sig.pos <- sig.pos[-(1:bn)]
上記の計算には約2秒ほどかかりました.
MCMCpackの方法と同じギブスサンプリングを用いていますが,フルスクラッチによる方法はR上で単純なfor文を使った実装なので,その点で計算時間に違いが出てきているのかもしれません.
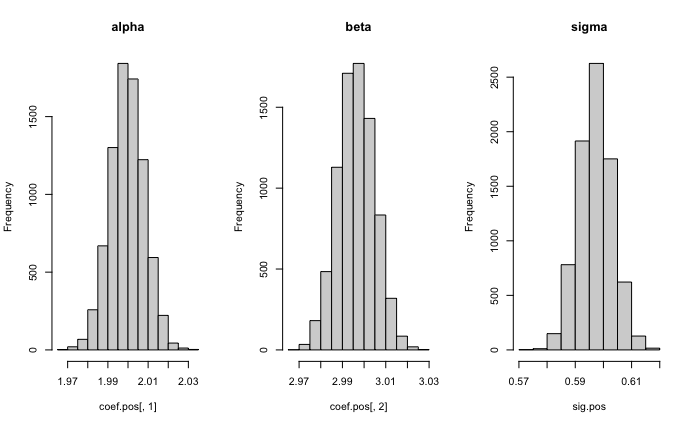
最後に事後分布の結果を図示します.
par(mfcol=c(1,3))
hist(coef.pos[,1], main="alpha")
hist(coef.pos[,2], main="beta")
hist(sig.pos, main="sigma")
この結果はStanやMCMCpackによるものとほぼ同じになっています.
まとめ
単純な線形回帰モデルのケースにおいてStan, MCMCpackによるベイズ推定とフルスクラッチによる推定方法を比較してみました.
今回扱ったモデルは単純なものなので,(コンパイル時間を除いては)StanとMCMCpackの計算時間に大きな違いはなかったですが,階層モデルなどで比較してみると計算時間が変わってくるかもしれません.
また,直接的にMCMCpackが適用できない問題設定においてはフルスクラッチでの実装がStanによる実装よりも高速になるという可能性も考えられます.
より複雑なモデルでの計算時間や結果の比較についても今後紹介していこうと思います.
株式会社Nospareでは統計学の様々な分野を専門とする研究者が所属しております.統計アドバイザリーやビジネスデータの分析につきましては株式会社Nospareまでお問い合わせください.