数列
$$a_n = (1 + \frac{1}{n})$$
のとき,nが∞に近づくならば$a_n$は1に近づく.(図1)
これは直感的に理解できるが次はどうだろう.
 図1
図1
これは図2のようにe=2.718... に近づく
$$a_n = (1 + \frac{1}{n})^n$$
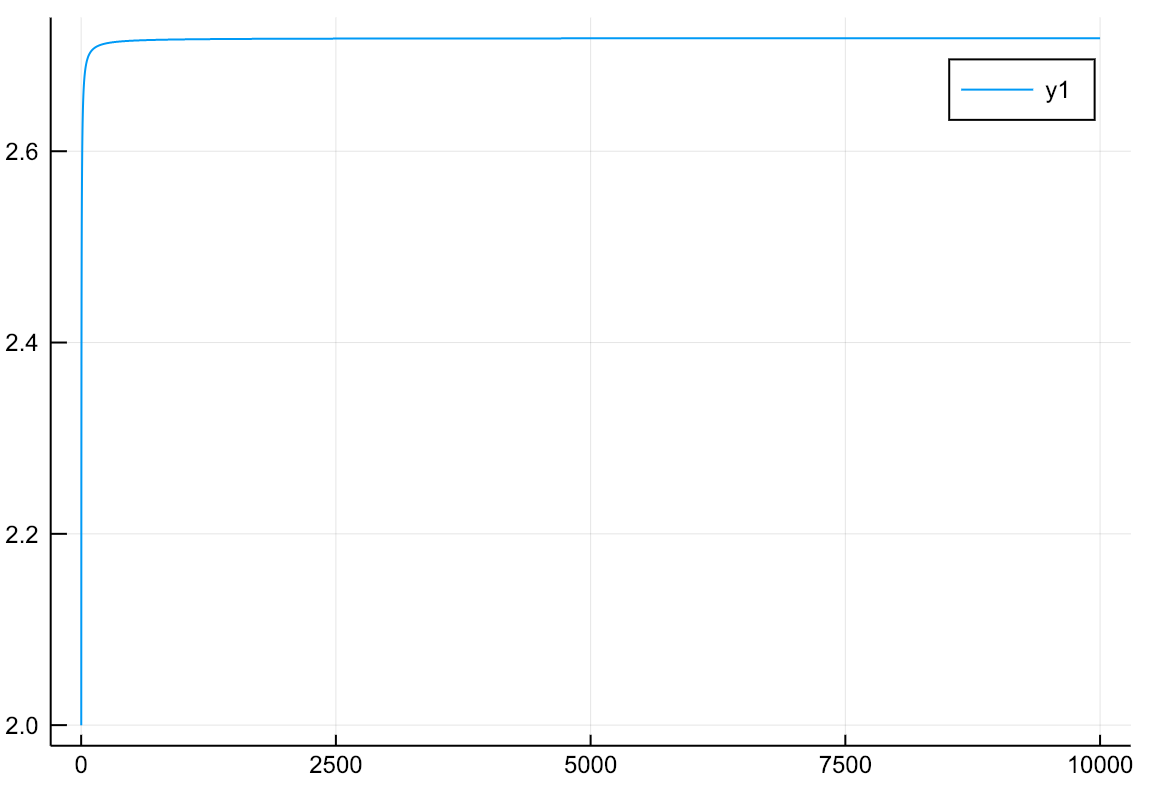
図2
しかし上では1に近づくならば1×1×1×....ならば1であると考えるのが人間の直感的な感想ではないだろうか.
しかしそうではない.そのために数列の収束を示す必要がある.
今回は$\epsilon$-近傍で定義することにしよう.
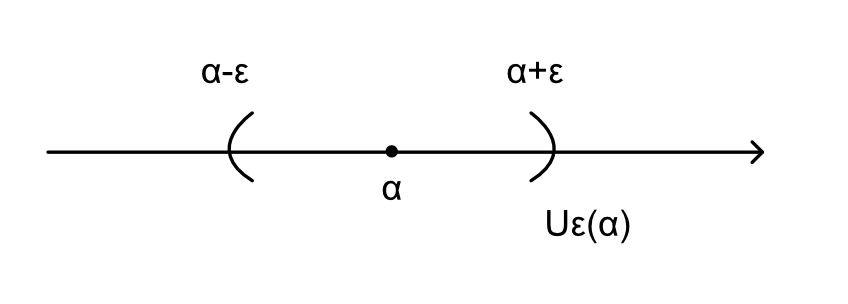
実数列$\{a_n\}^\infty_{n=1}$がある実数$\alpha \in \mathbb{R}$に収束することの厳密な定義を与えるため,$\alpha \in \mathbb{R}$を含む開区間$U_\epsilon(\alpha)$を次のように定義する.
$$ U_\epsilon ( \alpha ) = \{ x \in \mathbb { R } | \alpha - \epsilon < x < \alpha + \epsilon \} $$
$$ = \{ x \in \mathbb { R } | | x - \alpha | < \varepsilon \} \subset \mathbb { R }$$
を, 点$\alpha \in \mathbb{R}$の$\epsilon$-近傍と呼ぶ.
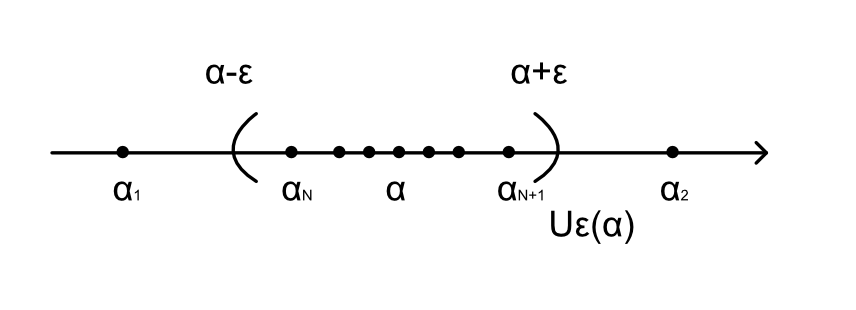
実数列$\{a_n\}^\infty_{n=1}$が実数$\alpha \in \mathbb{R}$に収束するとは,点$\alpha$のどんなに小さな$\epsilon$-近傍$U_\epsilon(\alpha)$に対しても(すなわち正の実数$\epsilon > 0$をどんなに小さく選んでも)
ある番号$N\in \mathbb{N}$より先の$a_N,a_{N+1},a_{N+2},\cdots$ はすべて$U_\epsilon(\alpha)$に含まれることであると定義する.
他にもイブシロン・デルタ論法を使って上での定義を書くこともある.
収束条件などは書けば長くなるので次回以降とする.