はじめに
よくシグモイド関数をグラフでみてこの関数は滑らかであるということが多いですが,滑らかとはなにかということを数学的に簡単に説明するのが目的です.微分の計算にはWolframAlphaを使いました.
一部のDeepLearningの書籍を見ると「見た目」に言及して、シグモイド関数は滑らかな関数であると言う記述がありました.見た目で滑らかだから学習がうまくいくのでしょうか?この記事でも詳しく言及できたわけではありませんが見た目で滑らかであるということは危険であるということを伝える内容であります.
微分可能とは
連続な関数f(x)について,右側微分係数$f'+(a)$と左側微分係数$f'-(a)$が存在して,$f'+(a) = f'-(a)$となるとき,$f(x)$は$x=a$で微分可能であるという.
$$f'+(a) = \displaystyle \lim_{h \to +0}\frac{f(a+h)-f(a)}{h}$$
$$f'-(a) = \displaystyle \lim_{h \to -0}\frac{f(a+h)-f(a)}{h}$$
シグモイド関数
$$sigmoid = \frac{1}{1+e^{-ax}}=\frac{1}{1+exp(-ax)}$$
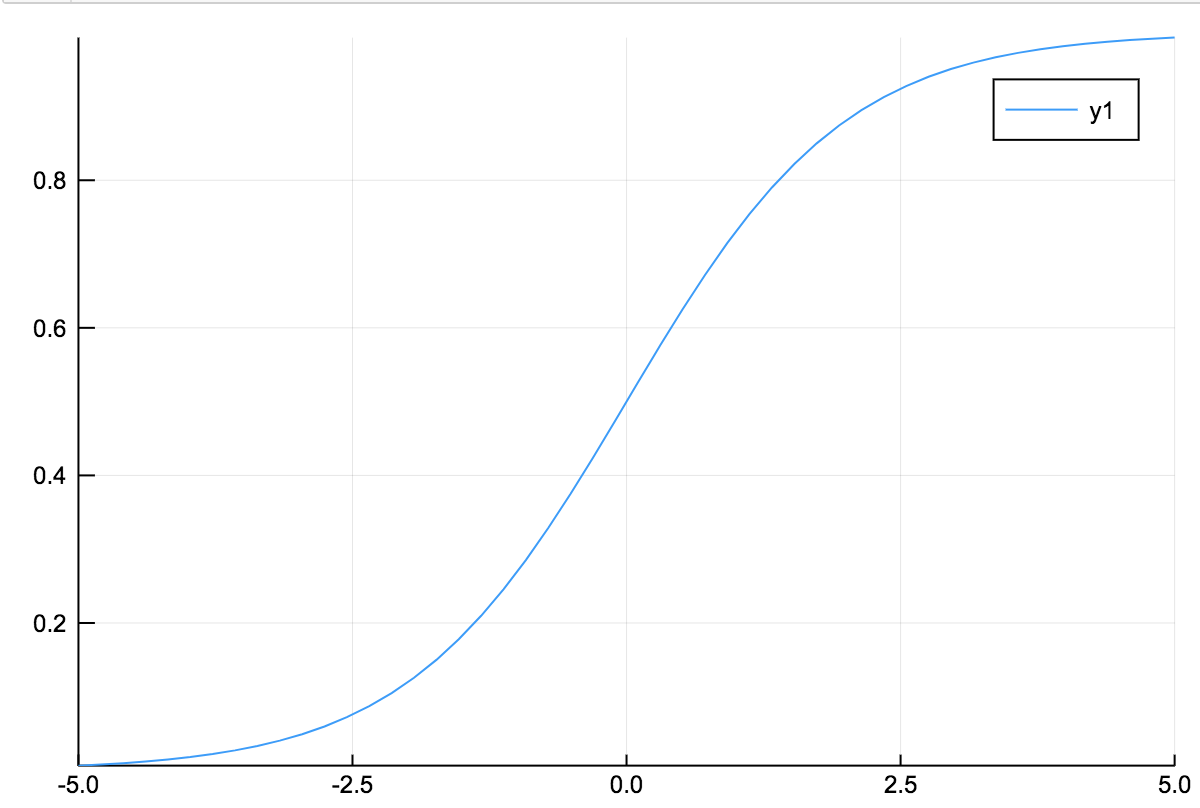
これは$(-5 \leq x \leq 5)$の時のシグモイド関数です.
これを見て滑らかな関数という書籍が一部でありますが,本当にそうでしょうか?
以下は$(-50 \leq x \leq 50)$のときのシグモイド関数です.一見微分可能ではないステップ関数のようにも見えてしまいます.見た目で滑らかだというのはナンセンスであり危険であるというのをおわかりいただけたでしょうか.

関数が連続であるとは
$x$が$a$に限りなく近づくならば,$f(x)$が$f(a)$に近づくとき関数$f(x)$は$x=a$のとき連続であるという.
これを数式で書くと以下のようになるとき連続であるといいます.
$\displaystyle \lim_{x \to a}f(x) = f(a)$
不連続である関数とは
代表的な次の3点を紹介します.
上の2つは点が不連続(つながっていない)であるため微分をすることはできません.

尖っている点(尖点)がある場合,極値での微分の値が存在しません.
滑らかな関数とは
関数$f(x)$が何度も微分可能であるときその関数は滑らかな関数であるといいます.(数学用語では十分大きなnに対して$C^n$級であるときに滑らかな関数)
そこで実際に微分してみましょう.
$$f'(x)=\frac{ae^{ax}}{(e^{ax}+1)^2}$$
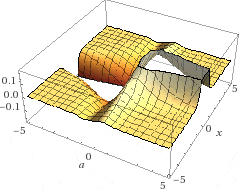
$$f''(x) = \frac{a^2e^{ax}(e^{ax}-1)}{(e^{ax}+1)^3}$$
$$f'''(x) = \frac{a^3 e^{ax}(-4e^{ax}+e^{2ax}+1)}{(e^{ax}+1)^4}$$
$$f''''(x) = \frac{a^4 e^{ax}(11e^{ax}-11e^{2ax}+e^{3ax}-1)}{(e^{ax}+1)^5}$$
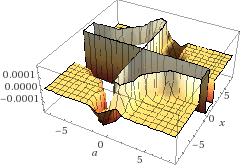
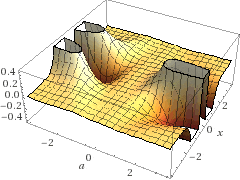
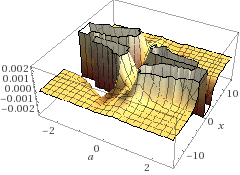
便宜上4階微分までとさせていただきましたが,3次元プロットをみると全然滑らかなグラフにはなっていませんね.3次元を見ることに意味があるのかは私には分かりません.
ですが滑らかな関数を考えるときに連続的微分可能な関数を考えているので無関係と考えるのも早いのかなと思います.
参考
「なめらかな関数」
https://ja.wikipedia.org/wiki/%E6%BB%91%E3%82%89%E3%81%8B%E3%81%AA%E9%96%A2%E6%95%B0
おわりに
グラフをみて滑らかであるというのがナンセンスだと思うので数学的に考えることは大切だと分かっていただけたでしょうか.また滑らかな関数と言っても拡大縮小すると結果は異なります.(上の図参照)
なので区分的に滑かという表現になるのだと思います.
滑らかだといっているの実際は,(区分的に)滑らかだというニュアンスが含まれているのだと思います.