トポロジーとは
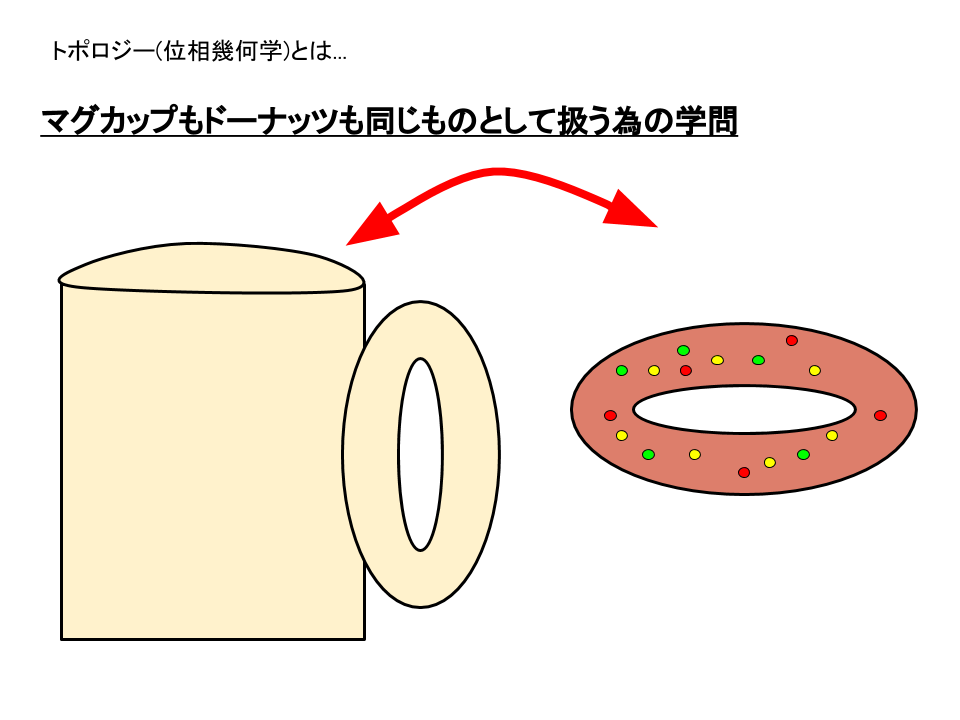
トポロジーとは図形のつながり具合を研究する数学の学問です.日本語では位相幾何学といいます.ぐにゅ〜と図形を潰した時の図形の穴の数を研究する立派な学問です.
(例: コーヒーカップとドーナツはトポロジーで見ると同じとします.数学用語ではイソトピー:isotopyとか日本語では同相と言います.)
しかし数学では,「ぐにゅ〜と潰した時の穴の数」では,お偉い様がたが許してはくれません.
そのためにホモロジー群を用いて,「ぐにゅ〜と潰した時の穴の数」ではなく,しっかりと万人にも分かる言葉で定義します.
ホモロジーとは
トポロジーという学問の中にホモロジーがあるというのが正しい包含関係でしょうか.
図形の形を定義するためにホモロジー群があるという感じです.
次は定義の方法です.
ホモロジーの定義の方法はいくつかあります.
・単体複体のホモロジー
・特異ホモロジー
・胞体ホモロジー
本記事では単体複体のホモロジーで紹介します.
チェインの定義
$G=(V,E)$をグラフとする.グラフの1チェイン,0チェインを次で定義する.
C_1(G) = \mathbb{Z} \langle E \rangle \\
= \{ x_1e_1 + x_2e_2 + \cdots + x_re_r | x_1,\dots, x_r \in \mathbb{Z}, e_1,\dots ,e_r \in E \} \\
C_0(G) = \mathbb{Z} \langle V \rangle \\
= \{ y_1v_1 + y_2v_2+ \dots + y_sv_s | y_1, \dots ,y_s \in \mathbb{Z}, v_1,\dots ,v_s \in V \}
$C_1(G)$の元を1次元チェイン,1チェインと呼びます.
また,$C_0(G)$の元を0次元チェイン,0チェインと呼びます.
複体の定義
$C_0,C_1,C_2,\cdots,C_n$を加群とする.これらを一列につなぐような
0\xrightarrow{\delta_{n+1}} C_n \xrightarrow{\delta_n} C_{n-1}
\xrightarrow{\delta_{n-1}} \cdots \xrightarrow{\delta_2} C_1 \xrightarrow{\delta_1} C_0 \xrightarrow{\delta_0} 0
というn+2個の準同型写像$\delta_{n+1},\delta_n,\cdots, \delta_1 ,\delta_0$が存在して,
\delta_{n+1} \circ \delta_{n} =0 \quad (i=0,1,\cdots,n)
を満たすときこれを複体という. [1]
単体複体の定義
次の二つの条件を満たすとき,単体複体といいます. [2]
(1) $ \sigma \in K$に対し,$\sigma$のどの辺単体も$K$に属する.
(2) $\sigma, \tau \in K$が$\delta \cap \tau \neq 0$を満たすとき$\delta \cap \tau$は$\delta$の辺単体であり,$\tau$の辺単体でもある.
複体のホモロジー群の定義
0 \xrightarrow{\delta_{n+1}} C_n \xrightarrow{\delta_n} C_{n-1}
\xrightarrow{\delta_{n-1}} \cdots \xrightarrow{\delta_2} C_1 \xrightarrow{\delta_1} C_0 \xrightarrow{\delta_0} 0
が複体であるとする.このとき,$Z_i,B_i$を
Z_i = \mathrm{Ker}\,(\delta_i)=\{ \alpha \in C_i \,|\, \delta_i(\alpha) = 0 \} \subset C_i \\
B_i = \mathrm{Im}\,(\delta_{i+1}) = \{ \alpha \in C_i \,|\, \exists \beta \in C_{i+1}, \delta_{i+1}(\beta) = \alpha \} \subset C_i
と定める.$Z_i$は$i$次輪体($i$サイクル)と呼ばれる.そこで$i$次元ホモロジー群を
H_i(C)=\frac{Z_i}{B_i}
により定義する.[1]よりそのまま参照.
パーシステントホモロジーとは
どうして上手くいくのか
完全に理論的にパーシステントホモロジーを用いて,解析する手法がどのような理論的な背景の上に上手くいくのか私に説明する力は無いので,大体の概略を説明します.
以下のGIFはfiltrationの過程を図示したものです.
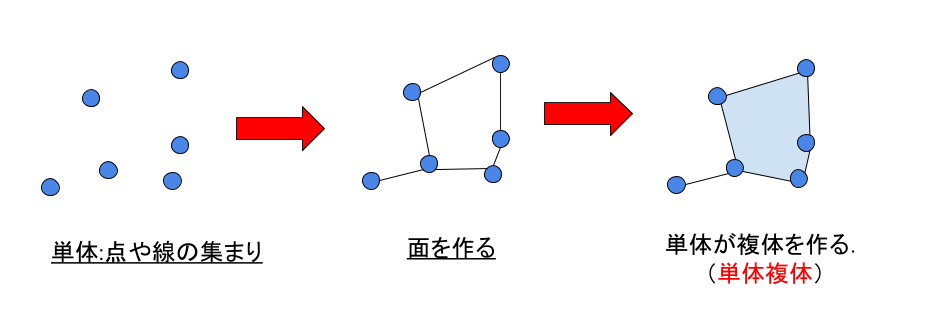
なぜこんなことをするかと言えば,ただの点では関係を見つけることができなので,単体複体にしたいからです.
詳しくは平岡裕章さんのスライドを参照してください.
(※geogeblaの作成のミスで点の一部の円周がfiltrationされていませんが,本来は全部filtrationの対象です.)
GIFは最初の円周が0の時は穴が0の状態で円周が全て接した瞬間(単体複体になった時)に穴があるときをBirthで全ての円周が重なり穴がなくなった瞬間がDeathです.
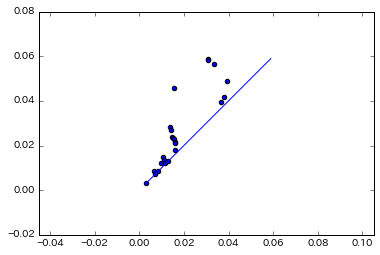
それを図にしたのが以下のPD図です.
PD図の特徴は
- PDの各点はデータ内の穴
- 発生軸は穴の発生パラメータ
- 消滅軸は穴の消滅パラメータ
- 対角線付近の点はノイズ
- 対角線から離れた点はロバスト
[4]より
実用例
機械学習,確率・統計,コンピュータビジョンなどにも応用されてアプリケーションも多いようです.
実際に応用してみる.
使用したソフトウェア
Dmitriy Morozovさんが書いたDionysusを使用しました.
Dmitriy Morozovさんのホームページ
pip install dionysus
でインストールできます.
import dionysus as d
import numpy as np
points = np.random.random((100, 2))
# ランダムな点からVietoris–Rips complex(単体複体)を作る.
f = d.fill_rips(points, 2, 1.)
p = d.homology_persistence(f)
dgms = d.init_diagrams(p, f)
# PD図をプロットします.matplotlibはライブラリの内部で宣言しているので
# importの必要はない.
d.plot.plot_diagram(dgms[1], show = True)
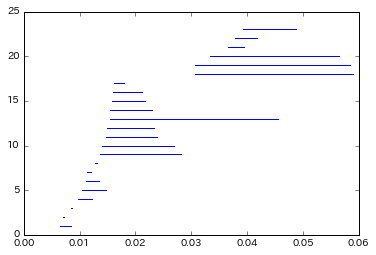
# バーコードの出力もできる.
d.plot.plot_bars(dgms[1], show = True)
a = np.random.random((800,800))
f_lower_star = d.fill_freudenthal(a)
p = d.homology_persistence(f_lower_star)
dgms = d.init_diagrams(p, f_lower_star)
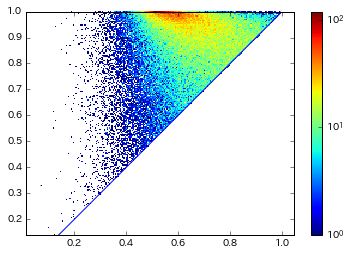
# 点密度のヒストグラムを表示.
d.plot.plot_diagram_density(dgms[1], show = True)
チュートリアルを参照.
http://mrzv.org/software/dionysus2/tutorial/plotting.html
まとめ
私は数学が得意な人間ではないので途中途中まちがった表現を用いているかもしれません.
その時は遠慮せず,編集リクエストやコメントでご指摘お願いします.
また,今回の記事はパーシステントホモロジーを普及させるためのまとめ記事として書きました.
自然言語処理に対しての応用はXiaojin Zhuさんが[5]にて指摘していますが,実際に試したいと思っています.単純なbag of words表現を利用しているようなので,試せれば追記で書きたいと思います.他にもパーシステントホモロジーは様々なアプリケーションで利用されているようです.[3]
参考文献
[1]計算で身につくトポロジー
[2]数学セミナー2017 12月号 (vol_56_no.12.674) p13 「ホモロジーの基礎」 田中心
[3] vitaliy kurlinさんのホームページより
[4]平岡裕章さんのスライド
[5]Persistent Homology
An Introduction and a New Text Representation
for Natural Language Processing