この記事を開いていただきありがとうございます。 地震界隈 Advent Calendar 2021 22日目の記事です。私は日本語に翻訳するために最善を尽くしましたので、ご理解いただければ幸いです。
はじめに
東日本大震災後、高層ビルの被害を特徴づける新たな規模が必要であることが明らかになりました。確かに、震源域から数百キロメートル離れた大阪市内（最大震度3）の超高層ビルで大きな揺れが発生し、エレベータの停止や閉じこめ、内装材等の破損が生じた [1]。
超高層ビルは低周波（=長周期 > 1.6秒）と共鳴する可能性のある背の高い構造物であるため、この損傷は長周期地震動 (英語 : Long-period ground motion, LPGM) によるものでした。震度階級は1秒以下の周期を考慮しているため、長周期地震動の特徴づけには適していません。これらの理由から、気象庁は長周期地震動に関する研究会を開きました。
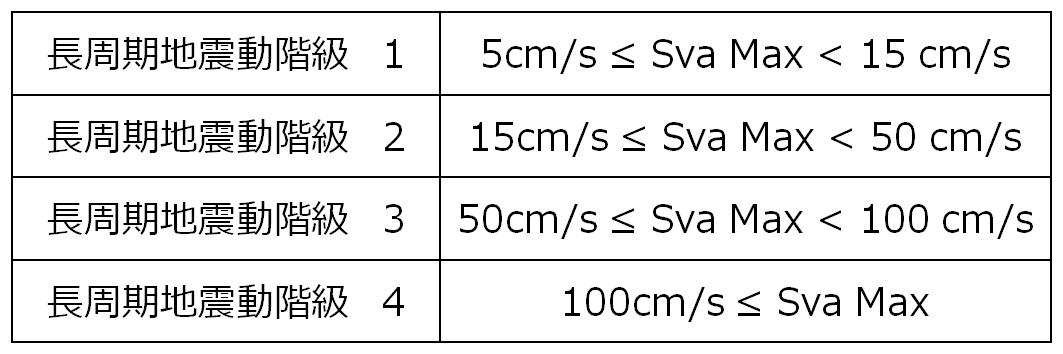
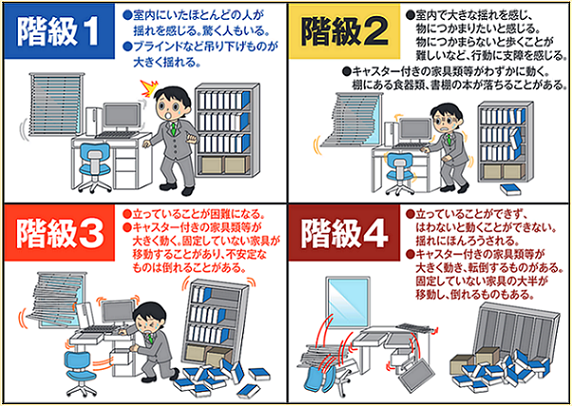
その後、「気象庁長周期地震動階級」の4段階を設定することが決定されました :
2019年11月より「長周期地震動観測情報」が本格稼働しました。
地震学に興味のある人として、加速度の記録から震度の測定値を取得する方法は知っていますが、長周期地震動の情報がどのように取得されるのか非常に興味がありました。
私の知る限り、計算方法はどこにも表示されないので、調査してPythonで実装し、共有することにしました。
関連するコードは、例を含むGithubリポジトリで入手できるため、自分で確認できます :
https://github.com/fleneindre/lpgm-calculator
計算方法
加速度波形から長周期地震動階級を計算することは容易ではありませんが、原理は理解しやすいです。
この方法の要点は、次の仮定にあります。背の高い垂直構造は、柔軟なロッドに取り付けられた塊のように機械的に動作します。
ダンピングは、構造内の摩擦をモデル化します（そのため、無期限に振動することはありません）。
この動画を見るとより明確になります:
各建物には独自の自然振動周期があります。 それはその高さとその構造の剛性に直接関係しています。さまざまな種類の高層ビルへの潜在的な影響を評価するために、長周期地震動階級の計算方法は、1.6〜7.8秒の周期で32個の仮想発振器の振動を評価することで構成されます。
具体的には、記録された加速度水平成分が32個の仮想発振器に入力されます。 次に、各発振器が到達する最大絶対水平速度（発振器速度+地動速度）が維持されます。 これは、相対応答速度スペクトル(Sva)と呼ばれます。
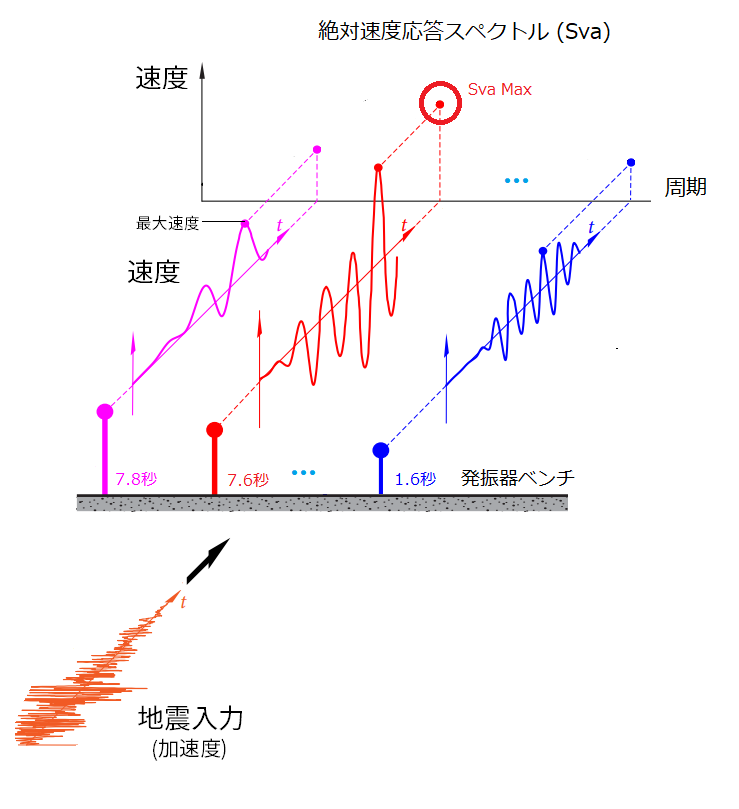
すべての値の最大値(Sva Max)は、長周期地震動階級を決定するしきい値と比較されます。
実装
提案された実装は、リアルタイム操作用に設計されています。 つまり、各ステージでは、新しい加速度サンプルを入力として、再帰式を使用する必要があります。
提案されたコードは、与えられた加速度計のサンプルレートからそれ自体を初期化するPythonクラスです。
lpgmCalculator = LPGMCalculator(sampleRate)
次に、3軸加速度 (np.array(,3))のすべてのサンプルをサンプルレートで提供する必要があります。 2つの最初のベクトル成分は水平成分でなければなりません。
while True:
...
LPGM = lpgmCalculator.update(rawAcc)
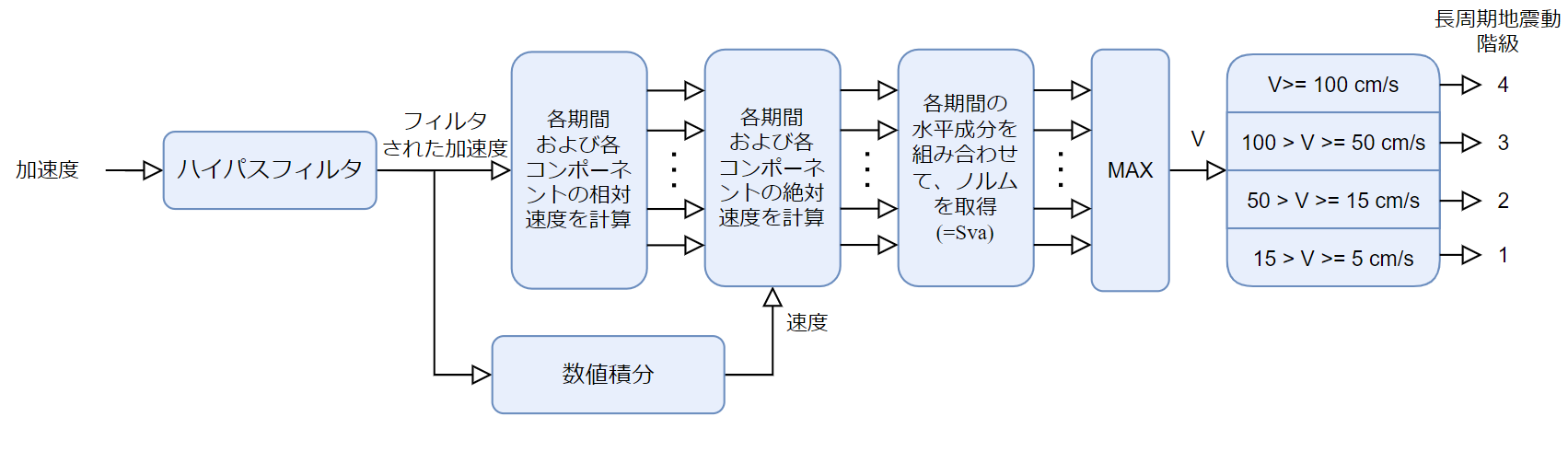
この更新手順は、次のフローチャートに従います
フィルタリング (HPF)
この方法では地盤速度を計算する必要があるため、ハイパスフィルタリングのステップが必要です。 このステップがないと、積分ステップでバイアスが発生するため、速度値が発散します。
[2]で説明したように、20秒 (0.05 Hz) をカットする2次のHPFを加速度記録に適用します。このようなフィルターの数値実装は再帰的に行われます。
# Filter the acceleration components
accHFi = self.bf[0]*self.accH + self.bf[1]*self.accH_1 + self.bf[2]*self.accH_2 \
- self.af[1]*self.accHF - self.af[2]*self.accHF_1
相対速度応答スペクトル
そうしさんと話し合って、私はSvaの計算方法を少し調べました。
相対変位スペクトルの再帰的計算について説明しているこの1969年の論文を見つけました [3]
行列演算を使用して、以前の状態と新しい加速度サンプルから発振器の変位と速度を計算します。
# Compute current oscillator horizontal relative velocity and displacement
self.xi[:,:,j] = np.matmul(self.A[:,:,j],self.xi[:,:,j]) + \
np.matmul(self.B[:,:,j],np.array([self.accHF_1[0:2],self.accHF[0:2]]))
AおよびBマトリックスは、発振器ごとに事前に計算する必要があります。
絶対速度応答スペクトル
Svaを決定するには、速度が必要であり、台形積分を使用して計算されます。
self.vel = self.vel + (self.accHF_1+self.accHF)*self.sampleTime/2;
次に、対応する水平コンポーネントに追加されます。 現在評価されている発振器のSva値は、水平成分の組み合わせから生じるノルムです[4]。
# Store the current oscillator absolute velocity norm
self.Sva[j] = np.sqrt((self.xi[1,0,j]+self.vel[0])**2+(self.xi[1,1,j]+self.vel[1])**2)
すべての発振器Svaの最大値がmaxSvaに保存されます
self.maxSva.appendleft(np.max(self.Sva))
長周期地震動階級
読みやすくするために、長周期地震動階級はmaxSvaの最後の30秒の最大値から決定されます
if self.maxSva30 < 5:
self.LPGM = 0
elif self.maxSva30 < 15:
self.LPGM = 1
elif self.maxSva30 < 50:
self.LPGM = 2
elif self.maxSva30 < 100:
self.LPGM = 3
else:
self.LPGM = 4
return self.LPGM
検証
提案された実施の妥当性を検証するために、記録された気象庁データとの比較が行われました。
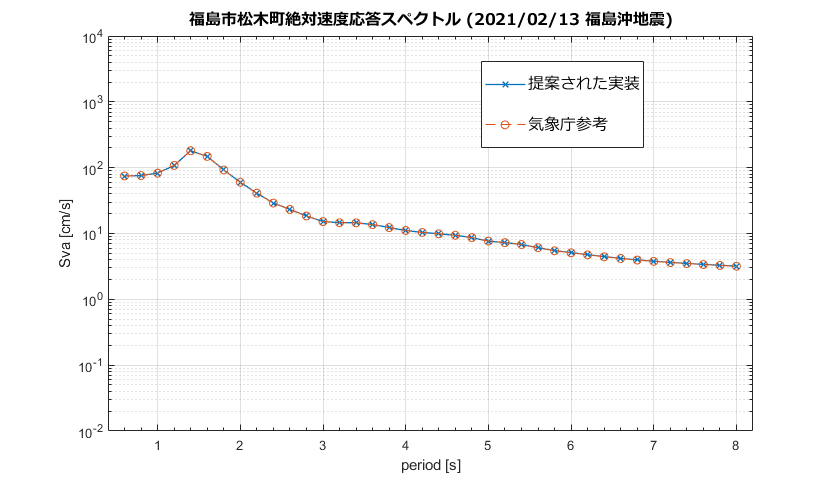
2021/02の福島沖地震データと比較することにしました。長周期地震動階級4を測定したので、福島市松木町観測点を選びました。
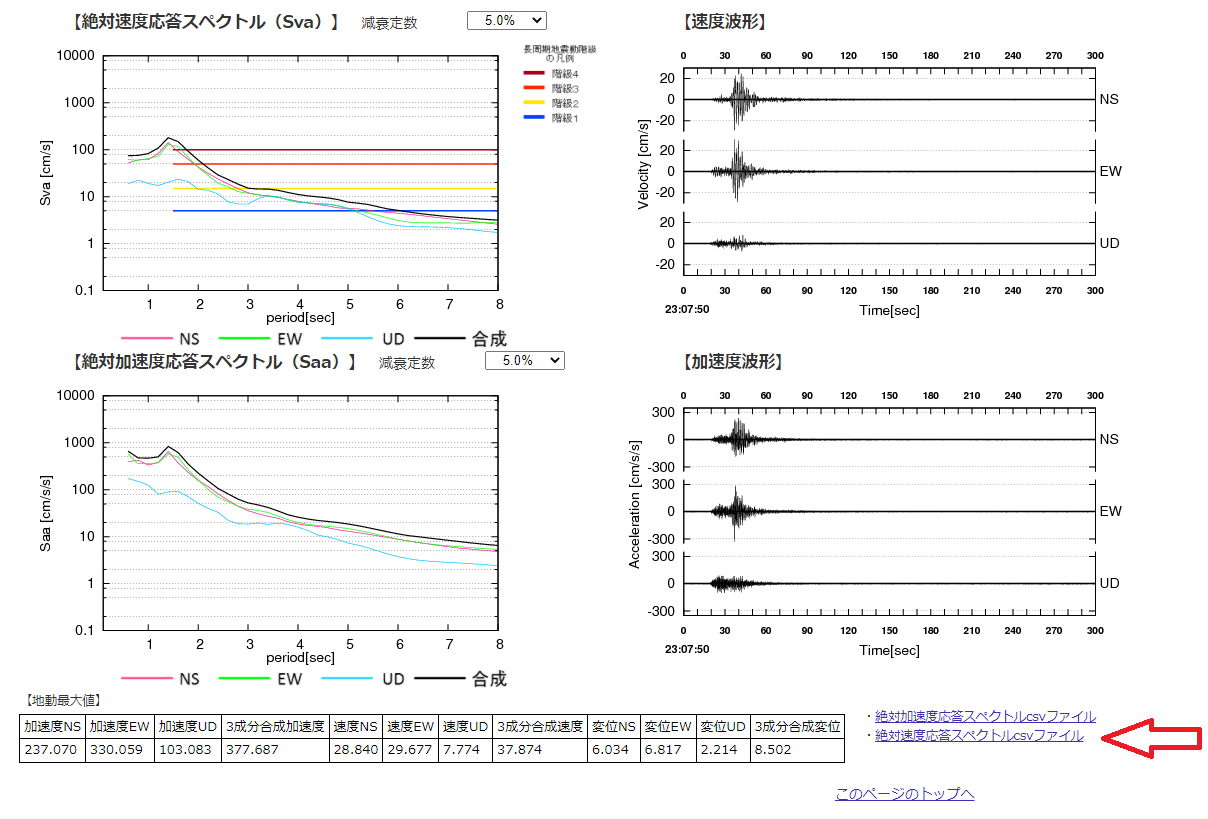
まず、このリンクから局加速度波形をダウンロードしました http://www.data.jma.go.jp/svd/eqev/data/kyoshin/jishin/2102132307_fukushima-oki/index.html
次に、このリンクから絶対速度応答スペクトルデータを取得しました http://www.data.jma.go.jp/svd/eew/data/ltpgm_explain/data/past/20210213230800/station/47595.html
データはページの下部にある.csvファイルとして入手できます。
ご覧のとおり、これは提案された実装と気象庁の参照データの間の完全な適合です。大成功 ！
結論
記事を読んでいただきありがとうございます！ とても技術的でしたが、怖がらないように数式は避けました。
楽しい（延長された）週末のプロジェクトでした。この貢献がお役に立てば幸いです。
使用する場合は、必ず建物の1階にセンサーを設置しましょうね。
ボーナス
これは松木町地震記録の操作を示すビデオです
書誌
[2] https://www.data.jma.go.jp/svd/eqev/data/study-panel/tyoshuki_joho_kentokai/kentokai7/siryou2.pdf
[3] Nigam, Navin C. and Jennings, Paul C. (1969) Calculation of response spectra from strong-motion earthquake records. https://authors.library.caltech.edu/47855/1/909.full.pdf
[4] https://www.data.jma.go.jp/svd/eqev/data/study-panel/tyoshuki_joho_kentokai/kentokai9/siryou6.pdf