まえがき
この記事は投稿者(NokonoKotlin)の個人サイトの記事から Qiita 用に移植 & 加筆したものです。 (この文言は記事が剽窃でないことを周知するためのものであり、個人サイトの宣伝ではないことをあらかじめご了承ください。)
前に同じような記事を出してたのですが、これはその記事の修正版です。
はじめに
みなさんはプログラムの限界を考えたことはありますか。つまり、もーこれ以上絶対無理だー!!といった状況にぶち当たったことはありますかっちゅってんの!!!😠
ぼくはあります。まさか次に述べることができるなんてまっさかそんなまっさか。
-
めちゃデカい範囲 ($10^{18}$ とか) を持つ配列で
std::vectorのような機能や区間操作を高速に実現する。
これはできます。詳しい機能は後述しますが、びっくりですよ奥さん。
普通、配列の index がめちゃんこデカくなる場合は座標圧縮などでデータの前処理が必要でしたが、それをせずに生のデータのまま扱えて嬉しいですね。
データ構造概要
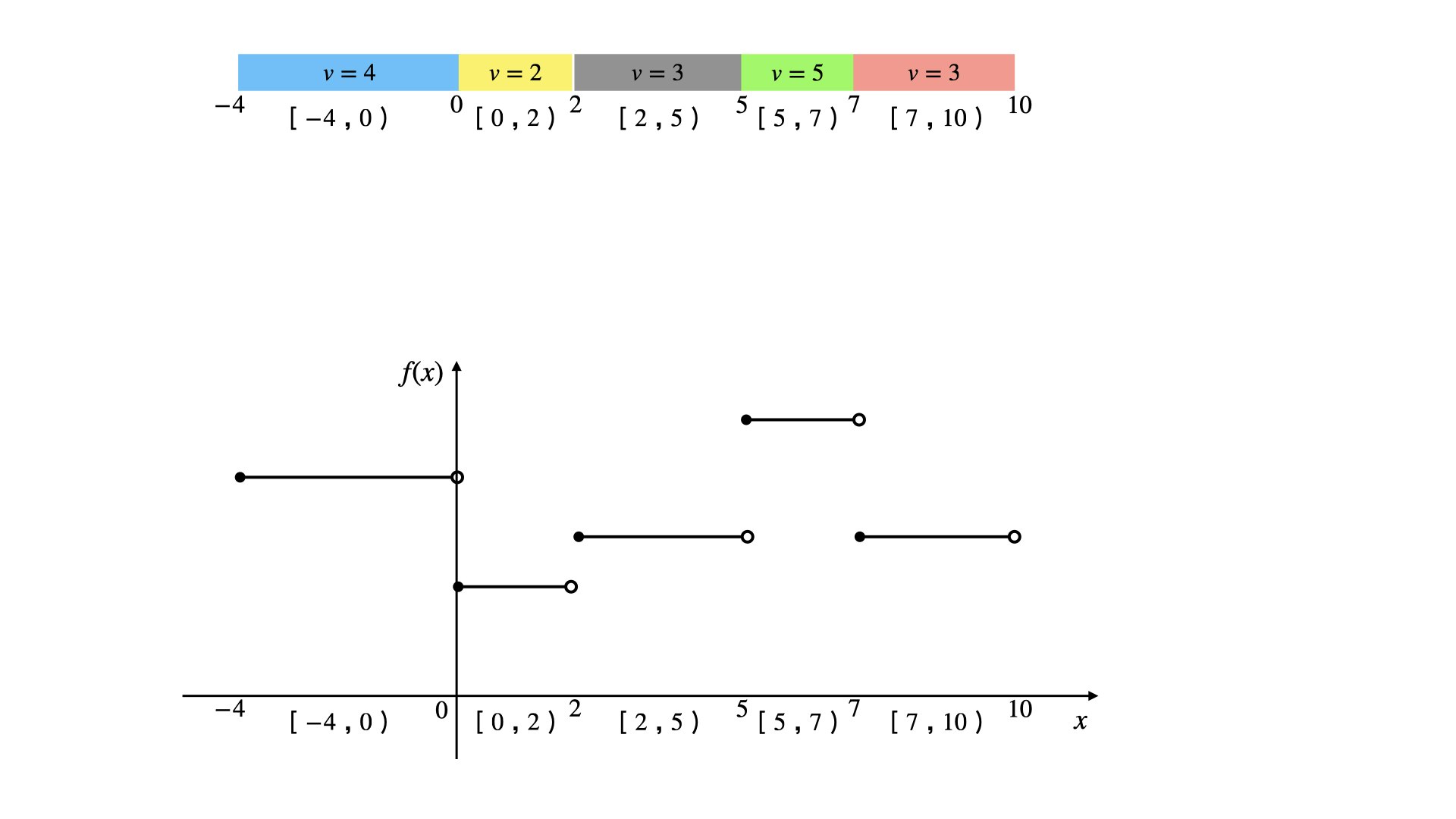
平衡二分木の各ノードに区間の両端の座標 : $ [l,r) $ と $v$ を持たせます。
区間内の座標は連続なので、ノードに持たせた値 $v$ は区間内の座標 $x$ に対する不連続な関数 $f(x)$ とみなすことができます。
このように考えることで 連続かつ範囲の制約がない実数値を配列の index のように振る舞わせることができます。このライブラリをメチャデカ配列 $F$ と呼ぶことにします。以下はこのメチャデカ配列で実現可能な操作の例です。$Q$ 回の処理を行う計算量は $O(Q\log{Q})$ 時間です。
- $\mathrm{RangeAffine}(l,r,A,B)$ : $x \in [l,r) $ について、$F[x] \leftarrow A\cdot F[x] + B$ とする。(区間アフィン変換)
- $\mathrm{RangeUpdate}(l,r,V)$ : $x \in [l,r) $ について、$F[x] \leftarrow V$ とする。(区間更新)
- $\mathrm{RangeSumQuery}(l,r)$ : $x \in [l,r) $ について、$F[x]$ の積分を計算する。(総和クエリ)
- $\mathrm{RangeMin(Max)Query}(l,r)$ : $x \in [l,r) $ について、$F[x]$ の最大値/最小値を計算する。
- $\mathrm{circular\_shift}(l,r,x)$ : $[l,r) $ 内の要素を右に x ずらす($r$ からはみ出た部分は左側に移動する)(区間シフト)。例えば数列 $(0,0,1,2,1,4)$ を右に $2$ ずらすと、$(1,4,0,0,1,2)$ となる。
- $\mathrm{RPush}(l,r,x)$ : 区間 $[l,r)$ の $F$ の値を $x$ にし、元々あった区間を右にずらす(区間挿入)。例えば $(1,5,2,2,1)$ の $1$ 番目と $2$ 番目の位置に $0$ を (同時に) 挿入すると $(1,0,0,5,2)$ になる(右端からはみ出た部分は消去する(後述)).
- $\mathrm{LPush}(l,r,x)$ : 区間 $[l,r)$ の $F$ の値を $x$ にし、元々あった区間を左にずらす。(区間挿入)
- $\mathrm{LErase}(l,r,x)$ : 区間 $[l,r)$ の関数 $F$ を削除し、空白になった区間 $[l,r)$ を左詰めで埋める(区間削除)。例えば $(1,5,2,2,1)$ の $1$ 番目と $2$ 番目を削除すると $(1,2,1,x,x)$ になる (右端で余った部分は $x$ で初期化する(後述)).
- $\mathrm{RErase}(l,r,x)$ : 区間 $[l,r)$ の関数 $F$ を削除し、空白になった区間 $[l,r)$ を右詰めで埋める。(区間削除)
冒頭に述べたように、メチャデカ配列の内部実装はノードが区間を持つ平衡二分木 です。以降、区間を管理する平衡二分木オブジェクトを $S$ とします。
$S$ は初期状態として $\mathrm{leftmost}$ と $\mathrm{rightmost}$ を区間として持つノードのみを持ちます。
設計
ここで、メチャデカ配列に関する重要な設計を書きます。
- 半開区間 $[\mathrm{leftmost} , \mathrm{rightmost}) $ の範囲外にアクセスしてはならない。
- 任意の $ x \in [\mathrm{leftmost} , \mathrm{rightmost}) $ に対して、$x$ をカバーする区間が $S$ にちょうど $1$ つ存在する。つまり $S$ が管理する区間は、$[\mathrm{leftmost} , \mathrm{rightmost}) $ を過不足なくきっちりカバーしているということです (区間を左から並べると、$[\mathrm{leftmost} , x_1) , [x_1,x_2) , [x_2,x_3),[x_3,x_4) \dots$ のようになっている)。
先述の $\mathrm{RPush}$ ではみ出た部分を削除したり、$\mathrm{LErase}$ で余った部分を $x$ で初期化するという処理は、この $[\mathrm{leftmost} , \mathrm{rightmost}) $ に関する設計思想があったからです。
また、重要な実装方針として以下の操作を定義します。
- $\mathrm{modify}(x)$ : 座標 $x$ をカバーする区間の $x$ の箇所に切れ込みを入れ($S$ にある区間を $x$ で分割する)、切れ込みの左右のノードを取得する。
区間 $[l,r)$ を取得する際に、$S$ の区間のみでちょうど $[l,r)$ をカバーするように整形すると、実装が非常に楽になります。
アフィン変換
$\mathrm{affine}(x,a,b) := ax + b$ を、$x$ に対するアフィン変換 $(a,b)$ と定義します。このメチャデカ配列では、与えられた半開区間 $[l,r)$ に対して、座標 $i$ ($i \in [l,r)$) に記録された値 $F[i]$ 全てに対してアフィン変換 $\mathrm{affine}(F[i],a,b)$ を行う操作として、区間アフィン変換 $\mathrm{RangeAffine}(l,r,a,b)$ を定義します。
具体的には、先に紹介した $\mathrm{modify}$ を用いることで、区間 $[l,r)$ に対応する Splay Tree の部分木を取り出し、その部分木にアフィン変換を遅延評価します。Splay Tree を使ってるので、詳しくは Splay Tree の記事を参照してください。
$x$ に対するアフィン変換 $\mathrm{affine}(x,a,b)$ は、$2$ つのパラメータ $(a,b)$ で決定されるので、この $(a,b)$ を遅延評価として保持します。特に、既に $(a_1,b_1)$ の遅延評価を持つノードに新たに遅延評価 $(a_2,b_2)$ が加わるとき、二つの遅延評価をマージした $({a_1}{a_2} , {a_2}{b_1} + b_2)$ を新たな遅延評価として保持させることができます。
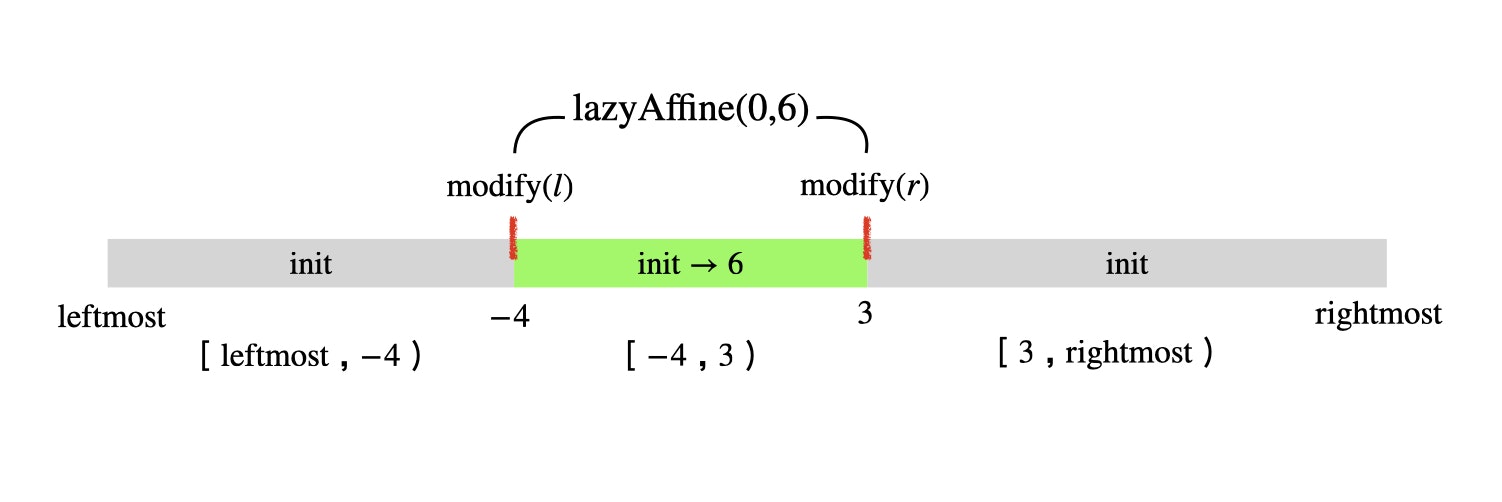
以下は $\mathrm{RangeAffine}(-4,3,0,6)$ の様子です。まずは $l = -4$ と $r = 3$ の地点に切れ込みを入れ、$[l,r)$ をカバーする部分木を取得し、その部分木の根にアフィン変換の遅延評価を載せる様子です。図では便宜上、遅延評価を持たせたことで既にアフィン変換の実行を完了したものとしてアフィン変換の結果を表示しています。
この例でお気づきの通り、アフィン変換 $(0,v)$ は元の値に $v$ を代入する操作です。このことから、区間アフィン変換と同時に区間代入も定義できます。以下はアフィン変換を用いて区間 $[0,6)$ に $1$ を代入する様子です。
次は、$x \in [-4,8)$ である $x$ に対して、$F[x]$ に $4$ 加算する操作の様子です。このような区間加算もアフィン変換で表現可能です。以下は $\mathrm{RangeAffine}(-4,8,1,4)$ の様子です。
区間シフト
$[l,r)$ 内の要素をスロットのリールのように右に x 移動させ、区間 $[l,r)$ からはみ出た部分は $[l,r)$ の左に移動する操作を $\mathrm{circular\_shift}(l,r,x)$ と定義します。ただし $|x| \leq r-l$ とします。以下は $\mathrm{circular\_shift}(-4,8,5)$ を行う様子です。
まず、以下の図で示す $3$ 点 $l , r-x , r$ に切れ込みを入れます。
切れ込みによって、区間 $[l,r)$ を $2$ つの区間 $[l,r-x)$ , $[r-x,r)$ に分割することができました。分割したそれぞれの区間をカバーする部分木を Splay Tree から取り出しておきます。ここも詳しくは Splay Tree の記事を参照してください。
その後、区間 $[l,r-x)$ に対応する部分木に、座標に $+x$ する遅延評価を加えることで、元々区間 $[l,r-x)$ を表していたノードたちを $[r-x , r)$ に対応づけます。
同様に、区間 $[r-x,r)$ に対応する部分木に、座標に $+(l+x-r)$ する遅延評価を加えることで、元々区間 $[r-x,r)$ を表していたノードたちを $[l , r-x)$ に対応づけます。
遅延評価を載せた結果、元の区間がスライドした (ものとして良い) ので、分割した部分木たちを対応する区間の順で連結します。
区間挿入/区間削除
最後に $\mathrm{RPush}(l,r,x)$ を紹介します。これまでに実装した機能を使うとシンプルに実装することが可能です。
区間挿入では右端 $\mathrm{rightmost}$ からはみ出た部分をは削除されるので、このことを利用します。$\mathrm{circular\_shift}(l,\mathrm{rightmost},r-l)$ を用いて、右端の長さ $r-l$ の区間を座標 $[l,r)$ に移動させます。その後、移動によって確保された区間 $[l,r)$ に対して $\mathrm{RangeUpdate(l,r,x)}$ を行うことで、あたかも新たに区間が挿入されたかのように振る舞います。
$\mathrm{LErase}$ は $\mathrm{RPush}$ の逆の操作をすれば良く、$\mathrm{LPush}$ や $\mathrm{RErase}$ も同じ話です。
ライブラリを書く際はいくつか注意点があります。
- $S$ において右端が $x$ 以下の区間の個数が、$x$ を含む区間の index になる
- $\mathrm{leftmost}$ や $\mathrm{rightmost}$ 周りへのアクセスは挙動が少し異なるので要注意
- 区間の長さが処理に必要なので、$\mathrm{leftmost},\mathrm{rightmost}$ をギリギリに設定するとオーバーフローする。
- 座標は連続なので、厳密に一点を $v$ に更新するといった操作ができないが、数列のように扱いたければ、$i$ 番目を半開区間 $[i,i+1)$ と言い換える。するとRangeSumQuery ,RangeUpdate なども数列の区間和クエリとして扱える。
ソースコード
使い方は後述します。あとコメントの英語が拙いのは気にしないでください。雰囲気がわかればいいのです。
ライセンスは守ってくださいね (このライブラリの冒頭に以下を書くだけで良いです)。
- Copyright ©️ (c) NokonoKotlin (okoteiyu) 2024. Released under the MIT license(https://opensource.org/licenses/mit-license.php)
ライセンスに従わない利用を確認した場合、ライセンスに従わない利用をやめるよう指示するなどの処置を取る場合があります。
#include <iostream>
#include <vector>
#include <cassert>
using namespace std;
/*
Copyright ©️ (c) NokonoKotlin (okoteiyu) 2024.
Released under the MIT license(https://opensource.org/licenses/mit-license.php)
*/
template<class T, class F >
class ExtendedArray{
private:
struct SplayNode{
SplayNode *parent = nullptr;
SplayNode *left = nullptr;
SplayNode *right = nullptr;
T R;
T L;
T length(){return R-L;}
T length_sum;
F Value;
F Sum;
F Min;
F Max;
int SubTreeSize = 1;
private:
bool copied_instance = false;
public:
SplayNode copy(){
assert(copied_instance == false);
SplayNode res = *this;
res.left = nullptr;
res.right = nullptr;
res.parent = nullptr;
res.copied_instance = true;
return res;
}
pair<bool,pair<F,F> > lazy_affine ={false , {F(),F()}};
void set_lazyAffine(F& a, F& b){
if(this->lazy_affine.first)this->lazy_affine.second = { a*this->lazy_affine.second.first , a*this->lazy_affine.second.second + b};
else this->lazy_affine = {true , {a,b}};
}
pair<bool,T> lazy_shift = {false,T()};
void set_lazyShift(T x){
if(this->lazy_shift.first)lazy_shift.second += x;
else lazy_shift.second = x;
this->lazy_shift.first = true;
}
SplayNode(){}
SplayNode(T l , T r , F Value_){
assert(l < r);
R = r;
L = l;
Value = Value_;
update();
}
void rotate(){
if(this->parent->parent != nullptr){
if(this->parent == this->parent->parent->left)this->parent->parent->left = this;
else this->parent->parent->right = this;
}
this->parent->eval();
this->eval();
if(this->parent->left == this){
this->parent->left = this->right;
if(this->right != nullptr)this->right->parent = this->parent;
this->right = this->parent;
this->parent = this->right->parent;
this->right->parent = this;
this->right->update();
}else{
this->parent->right = this->left;
if(this->left != nullptr)this->left->parent = this->parent;
this->left = this->parent;
this->parent = this->left->parent;
this->left->parent = this;
this->left->update();
}
this->update();
return;
}
int state(){
if(this->parent == nullptr)return 0;
this->parent->eval();
if(this->parent->left == this)return 1;
else if(this->parent->right == this)return 2;
return 0;
}
void splay(){
while(this->parent != nullptr){
if(this->parent->state() == 0){
this->rotate();
break;
}
if( this->parent->state() == this->state() )this->parent->rotate();
else this->rotate();
this->rotate();
}
this->update();
return;
}
void update(){
assert(copied_instance == false);
this->eval();
this->SubTreeSize = 1;
this->length_sum = this->length();
this->Min = this->Value;
this->Max = this->Value;
this->Sum = this->Value*this->length();
if(this->left != nullptr){
this->left->eval();
this->SubTreeSize += this->left->SubTreeSize;
this->length_sum += this->left->length_sum;
if(this->left->Min < this->Min)this->Min = this->left->Min;
if(this->left->Max > this->Max)this->Max = this->left->Max;
this->Sum += this->left->Sum;
}
if(this->right != nullptr){
this->right->eval();
this->SubTreeSize += this->right->SubTreeSize;
this->length_sum += this->right->length_sum;
if(this->right->Min < this->Min)this->Min = this->right->Min;
if(this->right->Max > this->Max)this->Max = this->right->Max;
this->Sum += this->right->Sum;
}
return;
}
void eval(){
assert(copied_instance == false);
if(this->lazy_affine.first){
this->Value = this->lazy_affine.second.first * this->Value + this->lazy_affine.second.second;
this->Min = this->lazy_affine.second.first * this->Min + this->lazy_affine.second.second;
this->Max = this->lazy_affine.second.first * this->Max + this->lazy_affine.second.second;
this->Sum = this->lazy_affine.second.first * this->Sum + (this->length_sum)*this->lazy_affine.second.second;
if(this->Max < this->Min)swap(this->Max,this->Min);
if(this->left != nullptr)this->left->set_lazyAffine(this->lazy_affine.second.first,this->lazy_affine.second.second);
if(this->right != nullptr)this->right->set_lazyAffine(this->lazy_affine.second.first,this->lazy_affine.second.second);
this->lazy_affine.first = false;
}
if(this->lazy_shift.first){
this->L += this->lazy_shift.second;
this->R += this->lazy_shift.second;
if(this->left != nullptr)this->left->set_lazyShift(this->lazy_shift.second);
if(this->right != nullptr)this->right->set_lazyShift(this->lazy_shift.second);
this->lazy_shift.first = false;
}
}
};
inline static constexpr bool CompareNode(SplayNode *a , SplayNode *b){return a->R <= b->R;}
SplayNode *get_sub(int index , SplayNode *root){
if(bool(root)==false)return root;
SplayNode *now = root;
while(true){
now->eval();
int left_size = 0;
if(now->left != nullptr)left_size = now->left->SubTreeSize;
if(index < left_size)now = now->left;
else if(index == left_size)break;
else{
now = now->right;
index = index - left_size-1;
}
}
now->splay();
return now;
}
SplayNode *merge(SplayNode *leftRoot , SplayNode *rightRoot){
if(leftRoot!=nullptr)leftRoot->update();
if(rightRoot!=nullptr)rightRoot->update();
if(leftRoot == nullptr)return rightRoot;
if(rightRoot == nullptr)return leftRoot;
rightRoot = get_sub(0,rightRoot);
rightRoot->left = leftRoot;
leftRoot->parent = rightRoot;
rightRoot->update();
return rightRoot;
}
std::pair<SplayNode*,SplayNode*> split(int leftnum, SplayNode *root){
if(leftnum<=0)return std::make_pair(nullptr , root);
if(leftnum >= root->SubTreeSize)return std::make_pair(root, nullptr);
root = get_sub(leftnum , root);
SplayNode *leftRoot = root->left;
SplayNode *rightRoot = root;
if(rightRoot != nullptr)rightRoot->left = nullptr;
if(leftRoot != nullptr)leftRoot->parent = nullptr;
leftRoot->update();
rightRoot->update();
return std::make_pair(leftRoot,rightRoot);
}
std::pair<SplayNode*,int> bound_sub(SplayNode* Node , SplayNode *root , bool lower){
if(root == nullptr)return std::make_pair(root,0);
SplayNode *now = root;
Node->update();
bool satisfy = false;
while(true){
now->eval();
if(lower)satisfy = !CompareNode(Node,now);
else satisfy = CompareNode(now,Node);
if(satisfy == true && now->right != nullptr)now = now->right;
else if(satisfy == false && now->left != nullptr)now = now->left;
else break;
}
int res = 0;
if(satisfy)res = 1;
now->splay();
if(now->left != nullptr)res += now->left->SubTreeSize;
return std::make_pair(now ,res);
}
pair<int,int> modify(T i){
if(i == leftmost)return {-1,0};
if(i == rightmost)return {SplayTreeSize()-1,SplayTreeSize()};
assert(leftmost < i && i < rightmost);
int it_ = lower_bound(i);
m_Root = get_sub(it_,m_Root);
m_Root->update();
if(i == m_Root->L)return {it_-1,it_};
if( i < m_Root->R ){
T nR = m_Root->R;
F V = m_Root->Value;
m_Root->R = i;
m_Root->update();
SplayNode* nnd = new SplayNode(i,nR,V);
nnd->update();
m_Root = bound_sub(nnd,m_Root,true).first;
if(!CompareNode(nnd , m_Root)){
if(m_Root->right != nullptr)m_Root->right->parent = nnd;
nnd->right = m_Root->right;
m_Root->right = nullptr;
nnd->left = m_Root;
}else{
if(m_Root->left != nullptr)m_Root->left->parent = nnd;
nnd->left = m_Root->left;
m_Root->left = nullptr;
nnd->right = m_Root;
}
m_Root->parent = nnd;
m_Root->update();
nnd->update();
m_Root = nnd;
}
return {it_,it_+1};
}
int SplayTreeSize(){if(m_Root==nullptr)return 0;return m_Root->SubTreeSize;}
int lower_bound(T x){
if(SplayTreeSize() == 0)return 0;
std::pair<SplayNode*,int> tmp = bound_sub(BluffObject(leftmost,x,F(0)),m_Root,true);
m_Root = tmp.first;
return tmp.second;
}
int upper_bound(T x){
if(SplayTreeSize() == 0)return 0;
std::pair<SplayNode*,int> tmp = bound_sub(BluffObject(leftmost,x,F(0)),m_Root,false);
m_Root = tmp.first;
return tmp.second;
}
SplayNode *m_Root = nullptr;
inline static SplayNode* const m_bluff_object = new SplayNode();
inline static SplayNode* const BluffObject(T l , T r , F f){
m_bluff_object->L = l;
m_bluff_object->R = r;
m_bluff_object->Value = f;
return m_bluff_object;
}
T leftmost ;
T rightmost;
void init(F init_value){
assert(leftmost < rightmost);
m_Root = new SplayNode(leftmost,rightmost,init_value);
}
void release(){
while(SplayTreeSize()>0){
pair<SplayNode*,SplayNode*> tmp = DeleteNode_sub(0,m_Root);
m_Root = tmp.first;
delete tmp.second;
}
}
public:
ExtendedArray(){}
ExtendedArray(T leftmost_ , T rightmost_ ,F init_v):leftmost(leftmost_),rightmost(rightmost_){init(init_v);}
ExtendedArray(const ExtendedArray<T,F> &x) = delete ;
ExtendedArray& operator = (const ExtendedArray<T,F> &x) = delete ;
ExtendedArray ( ExtendedArray<T,F>&& x){assert(0);}
ExtendedArray& operator = ( ExtendedArray<T,F>&& x){assert(0);}
void Reset(T leftmost_,T rightmost_ , F init_v){
leftmost = leftmost_;
rightmost = rightmost_;
init(init_v);
}
T Llimit(){return leftmost;}
T Rlimit(){return rightmost;}
SplayNode get(int i){
assert(0 <= i && i < size());
m_Root = get_sub(i,m_Root);
return m_Root->copy();
}
SplayNode GetRange(T lef , T rig){
assert(leftmost <= lef && lef < rig && rig <= rightmost);
int itl = modify(lef).second;
int itr = modify(rig).second;
std::pair<SplayNode*,SplayNode*> tmp = split(itr,m_Root);
SplayNode* rightRoot = tmp.second;
tmp = split(itl,tmp.first);
SplayNode res = tmp.second->copy();
m_Root = merge(merge(tmp.first,tmp.second),rightRoot);
return res;
}
void circular_shift(T lef , T rig , T x){
assert(leftmost <= lef && lef < rig && rig <= rightmost);
if(abs(x) == rig - lef)return;
if(x == T(0))return;
if(x < 0)x = rig-lef+x;
assert(0 < x && x < rig - lef);
T mid = rig - x;
int it_l = modify(lef).second;
int it_m = modify(mid).second;
int it_r = modify(rig).first;
assert(0 <= it_l && it_l < it_m && it_m <= it_r && it_r < SplayTreeSize());
pair<SplayNode*,SplayNode*> tmp = split(it_r+1 , m_Root);
SplayNode* p4 = tmp.second;
tmp = split(it_m,tmp.first);
SplayNode* p3 = tmp.second;
tmp = split(it_l,tmp.first);
SplayNode* p2 = tmp.second;
SplayNode* p1 = tmp.first;
p2->set_lazyShift(x);
p3->set_lazyShift(T(x-rig+lef));
p2->update();
p3->update();
m_Root = merge(merge(merge(p1,p3),p2),p4);
}
void RPush(T lef , T rig , F x){
assert(leftmost <= lef && lef < rig && rig <= rightmost);
circular_shift(lef,rightmost,(rig - lef));
RangeUpdate(lef,rig,x);
}
void LPush(T lef , T rig , F x){
assert(leftmost <= lef && lef < rig && rig <= rightmost);
circular_shift(leftmost,rig,-(rig - lef));
RangeUpdate(lef,rig,x);
}
void LErase(T lef , T rig , F init_){
assert(leftmost <= lef && lef < rig && rig <= rightmost);
RangeUpdate(lef,rig,init_);
circular_shift(lef,rightmost,-(rig-lef));
}
void RErase(T lef , T rig , F init_){
assert(leftmost <= lef && lef < rig && rig <= rightmost);
RangeUpdate(lef,rig,init_);
circular_shift(leftmost,rig,(rig-lef));
}
void RangeAffine(T lef , T rig , F A , F B){
assert(leftmost <= lef && lef < rig && rig <= rightmost);
int itl = modify(lef).second;
int itr = modify(rig).second;
std::pair<SplayNode*,SplayNode*> tmp = split(itr,m_Root);
SplayNode* t2 = tmp.second;
tmp = split(itl,tmp.first);
tmp.second->set_lazyAffine(A,B);
tmp.second->update();
m_Root = merge(merge(tmp.first,tmp.second),t2);
}
void RangeAdd(T lef , T rig , F x){
assert(leftmost <= lef && lef < rig && rig <= rightmost);
RangeAffine(lef,rig,F(1),x);
}
void RangeUpdate( T lef , T rig , F x){
assert(leftmost <= lef && lef < rig && rig <= rightmost);
RangeAffine(lef,rig,F(0),x);
return;
}
F operator [](T x){
assert(leftmost <= x && x < rightmost);
if(x == leftmost)return get(0).Value;
int it_ = upper_bound(x);
return get(it_).Value;
}
T size(){return rightmost - leftmost;}
void Debug(){
cerr << "DEBUG" << endl;
cerr << "L : " ;for(int i = 0 ; i < SplayTreeSize();i++)cerr << get(i).L << " ";cerr << endl;
cerr << "R : " ;for(int i = 0 ; i < SplayTreeSize();i++)cerr << get(i).R << " ";cerr << endl;
cerr << "V : " ;for(int i = 0 ; i < SplayTreeSize();i++)cerr << get(i).Value << " ";cerr << endl;
}
/*
Copyright ©️ (c) NokonoKotlin (okoteiyu) 2024.
Released under the MIT license(https://opensource.org/licenses/mit-license.php)
*/
};
使用例と機能
機能は先述の説明に加え、以下があります。
-
[i]で $F[i]$ の値を返す。 -
GetRange(l,r)は座標の半開区間[l,r)をカバーする部分木の根のコピーを返す。get()同様に、隣接頂点のポインタは封印されている。-
GetRange(l,r).Sumのようにして[l,r)の持つ要素のモノイド積を取得する
-
- index の型と値の型の 2 つをテンプレートパラメータにとる。
- コンストラクタには値の範囲である
[l,r)と、初期値の 3 つを渡す。
初期化
int main(){
// 単体で初期化 (index の型と値の型の 2 つをテンプレートに渡す)
// コンストラクタは index の範囲 [l,r) と初期化値の 3 つを渡す
ExtendedArray<long long,long long> F(-1e18,1e18,2);
// STL に乗せる場合
// コピー/ムーブは禁止なので、デフォルトコンストラクタで初期化する
vector<ExtendedArray<long long,long long>> EF(10);
// 後で 1 つずつ Reset を呼び出して初期化
for(auto& e : EF)e.Reset(-1e18,1e18,2);
EF[0].Debug();// ちゃんと初期化されているか確認
}
出力
DEBUG
L : -1000000000000000000
R : 1000000000000000000
V : 2
いろんな操作
int main(){
ExtendedArray<long long,long long> F(-1e18,1e18,2);
F.Debug();
cout << "区間 [-28587273,577284) の範囲の要素を全て -1 に変更" << endl;
F.RangeUpdate(-28587273,577284,-1);
cout << endl;
cout << "F[-1002994] = " << F[-1002994] << endl;
cout << endl;
cout << "区間 [48728,59928299387) の範囲の要素を全て 5 倍して 19 足す" << endl;
F.RangeAffine(48728,59928299387,5,19);
cout << endl;
cout << "F[395837712] = " << F[395837712] << endl;
cout << "F[188592] = " << F[188592] << endl;
cout << endl;
cout << "区間 [-577283,2995838) を右に 17772 だけ回転" << endl;
F.circular_shift(-577283,2995838,1772372);
cout << endl;
cout << "F[188592] = " << F[188592] << endl;
cout << endl;
cout << "区間 [1200004020,588828588828) に -10 を挿入し、元々の区間を右に押しやる" << endl;
F.RPush(1200004020,5888285838828,-10);
cout << endl;
cout << "F[2004928882893] = " << F[2004928882893] << endl;
cout << endl;
cout << "区間 [-29951200004020,588828588828293) の要素を全て削除し、" << endl;
cout << "空いた空間を自身より右の要素で詰める。さらにその右にできた空きを 0 で埋める。" << endl;
F.LErase(-29951200004020,588828588828293,0);
cout << endl;
F.Debug(); // デバッグ出力が少し見づらいのが難点
cout << endl;
cout << "区間 [104829833,999381220847266364) の総和クエリ -> " << F.GetRange(104829833,999381220847266364).Sum << endl;
}
出力
DEBUG
L : -1000000000000000000
R : 1000000000000000000
V : 2
区間 [-28587273,577284) の範囲の要素を全て -1 に変更
F[-1002994] = -1
区間 [48728,59928299387) の範囲の要素を全て 5 倍して 19 足す
F[395837712] = 29
F[188592] = 14
区間 [-577283,2995838) を右に 17772 だけ回転
F[188592] = 29
区間 [1200004020,588828588828) に -10 を挿入し、元々の区間を右に押しやる
F[2004928882893] = -10
区間 [-29951200004020,588828588828293) の要素を全て削除し、
空いた空間を自身より右の要素で詰める。さらにその右にできた空きを 0 で埋める。
DEBUG
L : -1000000000000000000 -29951200004020 999381220211167687
R : -29951200004020 999381220211167687 1000000000000000000
V : 2 2 0
区間 [104829833,999381220847266364) の総和クエリ -> 1998762440212675708