【入門】 基礎から理解するbit全探索

1. はじめに

皆さん、こんにちは!!!
競技プログラミング、楽しんでますか？ 私は、楽しんでいます(WAが出ていないときだけ)。

今回は、bit全探索について書きます。これは主観ですが、AtcoderのC問題が徐々に解けるようになってきた競技プログラマにとってbit全探索は、競技プログラミングにおいて、意外と最初の壁になったりすると思います。特に、数学が苦手な人だと、顕著かもしれません(実際、私も数学が苦手なので苦労しました)。

最近では、AtcoderのC問題として出題されることがあり、強くなるためには避けて通れません。
【ABC128 C - Switches】https://atcoder.jp/contests/abc128/tasks/abc128_c
【ABC147 C - HonestOrUnkind2】https://atcoder.jp/contests/abc147/tasks/abc147_c

というわけで、この記事では、例題を通してbit全探索を理解することを目標とします。強くなるために頑張っていきましょう！

(数学が苦手な人向けに書いたので冗長な表現があるかもしれませんが、得意な人は適宜読み飛ばして下さい)

2. 例題

以下に示すのが、今回解説に使用する問題です。

【問題】
$N$個の整数$A_i$が与えられます。$N$個の整数から、$0$個以上を選び和をとった値は、何通り存在するでしょうか？

【制約】
$1 \leqq N \leqq 8$
$1 \leqq A_i \leqq 100$

【例】
$N=3$
$A = \{1, 3, 4\} $

と入力されたとき、選び方は次の$8$通りありますが、和をとった値のうち$4$が重複していて答えは$7$通りになります。

• $0$（何も選ばない）
• $1$
• $3$
• $4$
• $1+3=4$
• $1+4=5$
• $3+4=7$
• $1+3+4=8$

以下、この例を使用して説明していきます。

3. bitで集合を管理する

突然ですが、bit全探索では、bitを利用して集合を管理します。これだけだと良くわからないので具体例を交えて説明します。

まずは、選ぶ数字にチェックマークを付けてみます。ここでは、$1$と$4$を選びます。

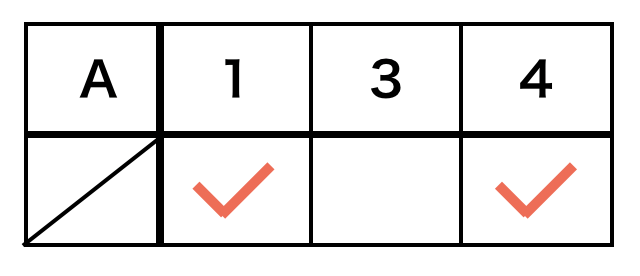
次に、チェックマークの代わりに$1$と$0$を使用することを考えましょう。選ぶ数字には$1$、選ばない数字には$0$をつけることとします。すると表は次のようになります。

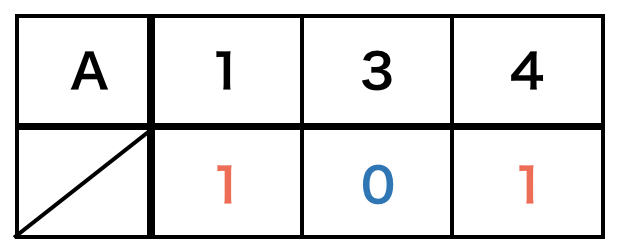
これでbit表現を用いて、集合$A$の部分集合$\{1, 4\}$を表すことが出来ました。
さて、部分集合$\{1, 4\}$を表すのに$101$というゼロイチの並びを使用しました。同様に、部分集合$\{1, 3\}$は$110$、部分集合$\{1, 3, 4\}$は$111$と表すことが出来ます。

以上より、「bitを用いて集合を管理することが出来る」というのがわかったと思います。

最後に、実装するときにbit列をどうやって持っておけば良いか考えます。
これは、集合を表すのに使用していたゼロイチの列(bit列)を2進数とみなして、10進数の整数に変換して持っておくのが良いです。
下の図に示しますが、部分集合を表す整数$s$を$0$から$2^N-1$までインクリメントするだけで部分集合を列挙できるからです。

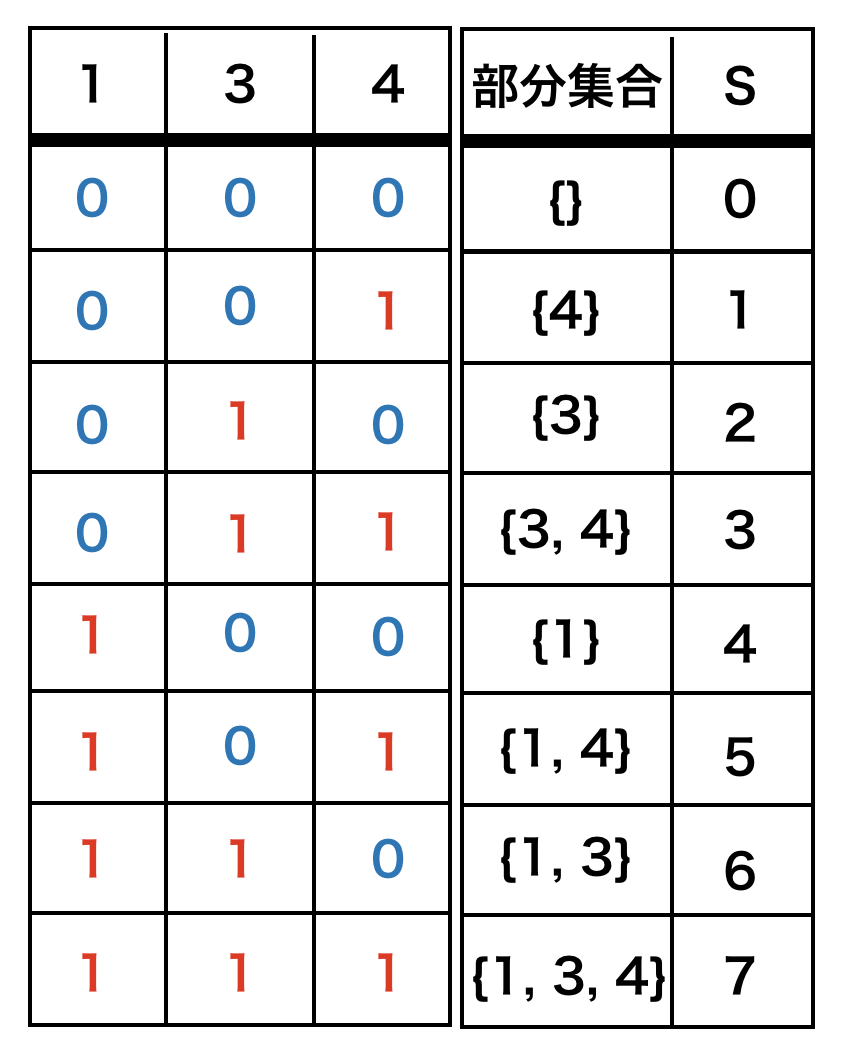
ここで、$2^N-1$までインクリメントする理由について説明します。
今回、$N$個の整数ひとつひとつに対して、(選ぶ/選ばない)の2通りが考えられます。よって部分集合は、場合の数としては$2^N$通り存在しますが、図を見て分かる通り、$1$つも選ばない時、つまり$s=0$のときを含めているため$2^N-1$までで良いです。もう一つの見方としては、$2^N$は、bitでみると$100...000$なので、$1$引くと繰り下がって$11...11$となり、結果$N$bitとなっていることがわかります。より直感的にいうと、選べる整数が$N$個しかないのに、チェック欄が$N+1$あるのは不自然なのでわかると思います。

また、2進数から10進数への変換は一意であり、$N$bit表現では、$0$から$2^N-1$までの整数しか表せないため、$0$からインクリメントしていくと、考えられる全ての0/1のパターンが現れるため、列挙することが出来ます。

4. 特定のbitが立っているかどうか判定する

前の章で、集合$A$の部分集合を0/1のbit列で管理し、実装時には、bit列を10進数に変換した値$s$として持っておくことにしました。
ここで、整数$s$がどんな部分集合を表しているのか知るにはどうしたらよいか考えてみましょう。真っ先に思いつくのは、2進数に変換して、特定のbitが$1$かどうか調べる、という方法でしょう。では、一体どのようにして、特定のbitが$1$かどうか調べればよいのでしょうか？ 答えはbit演算です。もっと具体的に言うと、$s$を右シフトして$1$とAND積を取ればよいです。

まずは、右シフトから説明していきます。
右シフトは、次のような計算をします。$s$を右に$1$回シフトすることは$s$を$2$で割ることと同義です。

また、C++において、右シフトは次のように書けます。

/*構文

s: 整数
i: 右シフトしたい桁数

// sを2進数で見た時にi桁右にずらす
s >> i
*/

// ビットで見ると 101
int s = 5;

// ビットで見た値は 10
int result1 = (s >> 1);

// ビットで見た値は 1
int result2 = (s >> 2);

// ビットで見た値は 0
int result3 = (s >> 3);

次に、bitごとのAND積について説明していきます。これは、bitごとにANDをとった結果が返ってきます。
$1$と整数$s$のbitごとのAND積を取ることで、一番下のbitがどうなっているかどうか知ることが出来ます。下に図を示します。

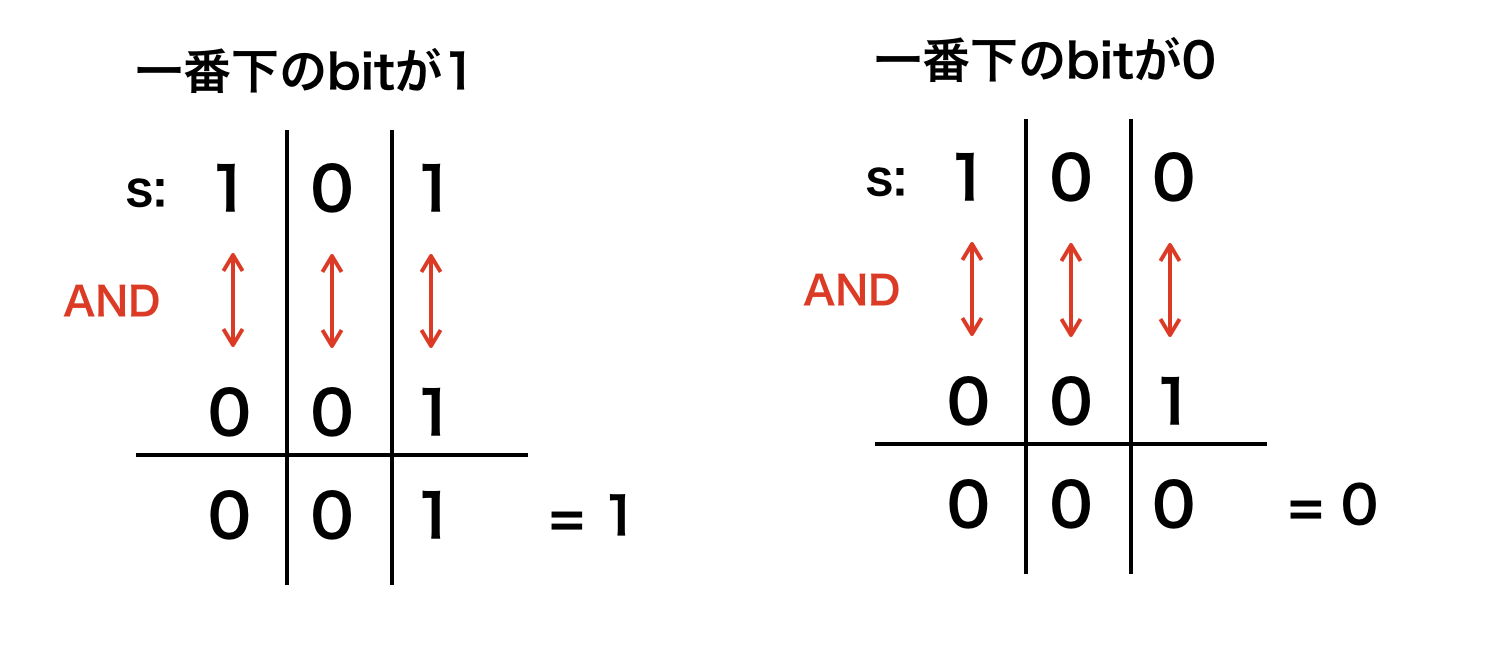
$0$とのAND積は、相手が何であろうと$0$のため、$1$とのAND積は、一番下のbitに着目すればよいです。
よって、$s$の一番下のbitが$0$であれば結果は$0$, $1$であれば結果は$1$となります。

以上より、特定のbitが$1$かどうか知るためには、右シフトをして$s$の一番下のbitをどんどん変えながら$1$との$AND$積を取って行けば良いことがわかります。これをC++で書くと以下のようになります。

// s: Nビット整数
for(int i = 0; i < N; i++){
    if((s >> i) & 1) cout << i << "th bit is 1" << endl;
}

5. bit全探索を実装する

いよいよ、bit全探索を使った例題を解くためのコードを実装していきます。
これまでに説明した知識の全てを総動員して行きます。総力戦です。

流れとしては、$s$を$0$から$2^N-1$までインクリメントして、部分集合を列挙していきます。
そして、$s$がどんな部分集合か調べるために、$s$右シフトしながら$1$とのAND積を取り、$i$番目のbitが$1$かどうか確認します。
bitが$1$であれば、それに対応する整数を選びます。
今回は、和が何通りあるか聞かれているので、重複があるかもしれません。なので和をsetにつっこんで数えます。
また、コード中では左シフト(1 << N)を使用していますが、これの結果は$2^N$となります。

#include <bits/stdc++.h>
using namespace std;

int main(){
    int N;
    cin >> N;
    vector<int> A(N);
    for(int i = 0; i < N; i++) cin >> A[i];

    set<int> ans;

    // sを0から2^N-1までインクリメントして部分集合を列挙
    for(int s = 0; s < (1 << N); s++){
        int sum = 0;
        //i回右シフトして、そのたびi番目のbitが1かどうか調べる。
        for(int i = 0; i < N; i++){
            //右シフトした後の整数sの最下位ビットが1かどうか、AND積をとって確認する。
            if((s >> i) & 1) sum += A[i]; //AND積の結果が1(i番目のbitが1ならば、i番目の整数を和に加える)
        }
        // setにつっこんで重複を削除する
        ans.insert(sum);
    }

    cout << ans.size() << endl;
}

6. あとがき

この記事を読んでbit全探索を理解する助けになったのであればとても嬉しいです。
わかりやすい記事を目指したつもりですが、まだまだ修行中の身のため、わかりにくい表現や間違いなどがあるかもしれません。
もし、発見した方は、遠慮なく突っ込んでくれればと思います。
読んでいただいてありがとうございました。