はじめに
この記事では、ABC179でE問題として出題されたSequence Sumという問題について説明します。
記事を書こうと思った動機としては、「なぜ今回の数列に周期性が存在するのか?」と疑問に思ったからです。
考えてみると周期性が存在するのは当たり前のことなのですが、しっかりと説明している記事が現時点では見当たらなかったので執筆することにしました。
E - Sequence Sumに登場する数列の周期性
この問題では、$A_{n+1} = {A_n}^2\ %\ M$ という数列について考えています。
以下、この数列が周期性を持つということを示していきます。
まず、数列の$i$項目を$A_i$とします。
すると、Modの定義より次の事がわかります。
0 \leqq\ {A_i}^2 \% M\ \leqq M-1\\
\Leftrightarrow 0 \leqq A_{i+1} \leqq M-1
この不等式からは数列のどの項も$0$以上$(M-1)$以下の値、つまり$M$通りの値しかとらないということがわかります。
次に、初項を$A_1$としてスタートし、第$M$項である$A_M$まで数列の値を求めたとします。
この時、第$1$項から第$M$項まで被りなし、つまり$A_i \neq A_j, \ (1\leqq i,j \leqq M)$だったとします。
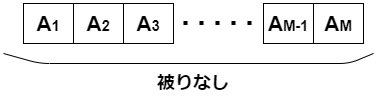
ここで、第$M+1$項目である$A_{M+1}$を求めると、数列の値は、上で述べたとおり$M$通りしかないので、今までに求めた値$A_i$と一致します。
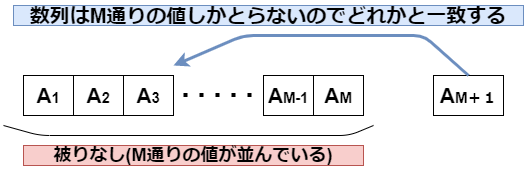
上の説明より、数列を有向グラフにすると次のように、サイクルの存在するグラフとして表せます。

以上より、$1\leqq i<j \leqq M$に対して$A_i = A_j$となる$i,\ j$が存在することがわかり、第$M$項まで被り無しで求められなかったとしても次のようなグラフで表現できることがわかります。

数列の値をどんどん求めていくと、いつかループし始めるというのが上の図からわかると思います。
よって今回の数列には周期性が存在することが示されました。
おわりに
まだまだ修行中の身なので、間違いや、わかりにくい表現があったら是非教えて頂けると嬉しいです。
もし、この記事の内容が役に立ったらLGTMをして頂くとモチベにつながります。
読んで頂きありがとうございました。