はじめに
この記事は「klis雑に愛を叫ぶ Advent Calendar 2018」の11日目の投稿です。
前日の記事は、麻綾( @Mayamaya_USM )さんによる「ポロンちゃんの布教」でした。
はてなブログに投稿しました
— 無職8歳児 (@Mayamaya_USM) 2018年12月9日
ポロンちゃんをみんな見てねーー!!! - 芋になりたいpotatorium https://t.co/W1nUhbWzjP #はてなブログ
深夜に失礼!!!!雑アド10日目です!
本記事の執筆を担当するのは、気合の鬼兄さん a.k.a. 気合(@nigensei848)です。klis16の代のすみっコぐらしで頭髪の育成に精を出しております。三つ編みとかよりもっとカワイイ感じのヘアアレンジがしてぇな?
今回は予定を変更して、主専攻実習のフォローアップ記事を書かせていただきます。予定されてた記事は本家の方で書こうかな~~
また、愛を叫ぶ対象としては、初等幾何学或いはグレブナー基底、若しくはmrtg先生♡でしょうか?(勢いが大事なので雑に叫びましょう、これ大切)なお、秋学期の主専攻実習定理証明班では2人脱落者が出ています(震え)
目次
- 主専攻実習について @知識情報システム主専攻
- 定理証明班(担当:mrtg先生)
- そもそも定理証明って?
- 証明したい数学的領域
-
グレブナー基底ってなんだよ -
図形とグレブナー基底とReduceをつなぐ - 具体的な手順(例:オイラー線)
- 感想とまとめ
- 参考文献
主専攻実習について @知識情報システム主専攻
2018年度シラバスを参照すると、知識情報・図書館学類知識情報システム主専攻における主専攻実習とは、“知識情報システム主専攻の専門科目に関連した実習を行う”ものとして書かれています。(p.196)
また、詳細を見てみると、
知識情報システムの構築に関わる基本的な技術を身につける。
知識情報システムを実現するための実践的な知識と技術 (問題の分解, クラス設計など) を身につ
ける。
・導入 (実習の説明, 知識情報演習の復習)(1 週目,7B206 集合)
・知識情報演習の成果を応用したシステムの構築 (2 週目~9 週目)
・発表 (10 週目)
・導入 (実習の説明)(1 週目,7B206 集合)
・知識情報システム構築など実習 (2 週目~9 週目)
1. 要求定義
2. システム設計
3. システム実装
・発表 (10 週目)
実習時間外に各グループで試行錯誤を繰り返しながら, 与えられた課題を完成させる。また, 夏
期休業期間中に, 秋学期の課題に必要なスキルアップを求めることがある。
上記のようになっています。
春学期はランダムに何人か選ばれ、グループとして何らかのシステムを自由な発想でつくりましたが、秋学期は自分で何をやるのかを選べます。そのうちの一つが、定理証明班(担当:mrtg先生)
定理証明班(担当:mrtg先生)
例年は片手に収まる程度の学生しか希望しないはずの定理証明班は、なぜか今年度は10人も集まりました。秋学期の主専攻実習の班分けは、春学期の主専攻実習の最終発表会が終わった後~夏休み前の任意のタイミングで行われます(記憶が定かではない)。なぜ多くなったのかと言うと、積極的理由と消極的理由の2つが重なったことにあると推察します。前者は、主に既に機械学習の基礎を理解していたが数学に不安があり、それを補うために意欲的に学ぼうとしたということ、後者は、Archivesを扱うbrisv班には行きたくないけど、あまりにもボリュームゾーンすぎるtdk班に行っても、十分な指導を受けられずふんわりとした理解で終わってしまうかもしれない(つまり消去法)ということです。まぁぼくがむやみに騒いで何人かの優秀パーソンを引き抜いたということも一因なのですが……
そもそも定理証明って?
その定理証明班が何をしていたのか?という疑問についてですが、簡単に言うと「計算機が定理を証明してくれたら嬉しいよね」ということを突き詰めるための初歩の初歩に挑んでいました。普通のプログラミング言語では〈計算〉は出来ても〈証明〉は中々難しいのですが、計算機数学の分野において発達した定理証明支援系というシステムを利用すれば、それがより簡単にできるようになる、ということらしいです(浅い理解)。
最近だと汎用的に使えるCoqとかがデファクト・スタンダードな模様ですが、分野によっては特化型が必要な場面もあるようです。今回のようにグレブナー基底をメインに据えて「簡約 reduce」するのであれば、その名の通り数式処理システムReduceを使うのが良さそう(なのかな?英語ばかりでわかりません幼子なので)。
証明したい数学的領域
まずいちばん簡単に証明しうるのは、「図形の性質」であるということらしいです。視覚的に捉えやすい上に、結果の検証も比較的容易です(ほんまか?)。
定理証明班においては、簡単な初等幾何学におけるグレブナー基底を利用した図形の定理証明をコンスタントに週イチくらいで行なってレポートを提出し、最終的に各個人が挑戦した一番難易度の高い or お気に入りの定理についてプレゼン資料をつくり、それについて説明するという発表を行いました。まぁここからまだ最終報告レポートをまとめるらしいんだけどそれはまた別の話。
グレブナー基底ってなんだよ
「方程式を解きやすいカタチに変換したもの」がグレブナー基底だと思ってください(投げやり)。詳しく説明しようとすると、「可換環」とか「イデアル」とか、数学の触れてはいけない領域に足を突っ込むことになります 難しい言葉がたくさん出てきてしまいます。むずかちムズカチだねぇ……
あ、どうやって変換するのかとかも秋学期序盤で血ヘド吐きながらReduceで実行させられました。**Buchberger's algorithm**というやつをひとつひとつ丁寧に理解していくレポートを書くためです(本来ならワンライナーで終わる操作を延々と手作業でやり直すにはかなりの精神力が必要とされるかもしれません(血涙))。
もし興味を持った人が居たら、ぜひ「最近、妹がグレブナー基底に興味を持ち始めたのだが。」を読んで〈グレブナー基底大好きbot(@groebner_basis)〉をフォローしましょう。フォローしろ。ポン酢も買え。
図形とグレブナー基底とReduceをつなぐ
さて、「これらをどのようにして使い証明していくのか」という話ですが、ともあれReduceは数式処理システムでありますから、図形を数式に置き換える必要があります。ここが私も一番初めに躓いた / 面食らったところです。
最終発表でも紹介しましたが、受講者はmrtg先生からいくつかの武器を与えられました。それが次の6つのユーザ定義関数(local定義関数)です。(詳細についてはここ)
1. 共線 Collinear # A-B-C
2. 中点 Mid point # mid M(A to B)
3. 平行線 Parallel lines # AB//CD
4. 直行線 Cross Vertical lines # AB⊥CD
5. 三平方の定理 Pythagorean theorem # AB^2 = BC^2 + CA^2
6. 正接 tangent # tan∠ABC = tan∠DEF
これらの定義関数に対して、座標軸上に与えられた点のX座標・y座標を適切に入力すれば、それに対応した数式(変形すると「=0」となるような関係の数式)が返ってくるようになっています。
こうして、
- 図形を座標軸上で考えて各点に座標を与える
- 図形の取りうる関係から「定義関数」を用いて
仮定と結論を導く - 得られた
仮定の数式群からグレブナー基底を求める(via Buchberger's algorithm) - グレブナー基底が得られたら、最後にそれを用いて
結論を表す数式を簡約する - 最終的に、簡約した結果が「=0」となれば、
仮定も結論もすべて「=0」であるということが言えて、自動的に正しいことが示される
と、このような理論体系になっています。すごい(こなみ)
数式処理システムReduceが登場するのは、このグレブナー基底を求める部分と、簡約を行う部分です。手作業でやるとクッソ時間が掛かるしその正確さも保証できないという阿鼻叫喚地獄絵図が生まれてしまいます……何度も言うけど実際に体験することになりますが……
具体的な手順(例:オイラー線)
知識情報システム主専攻_主専攻実習最終発表会 | Share and Discover Knowledge on LinkedIn SlideShare
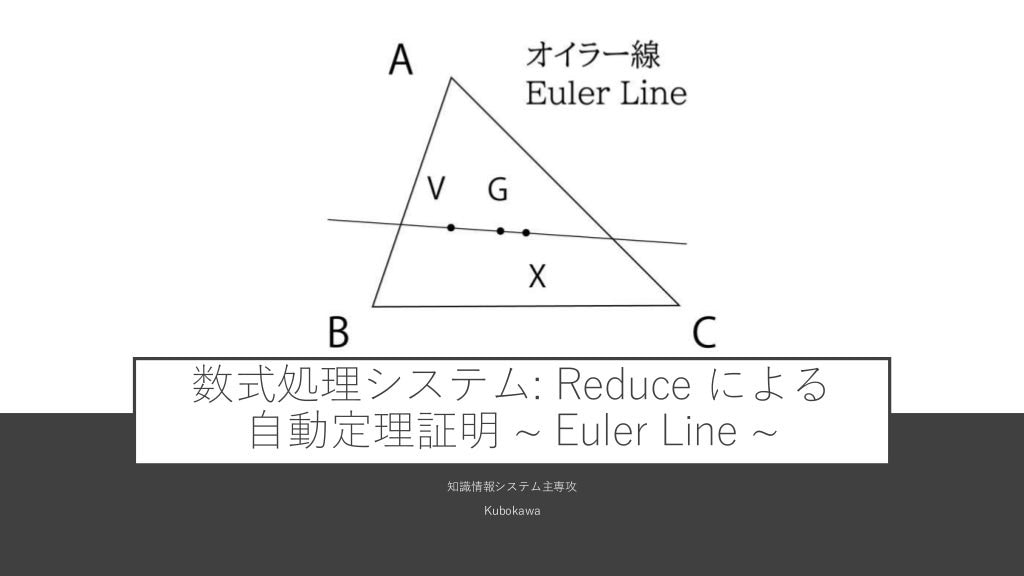
私が紹介したオイラー線について、発表時には説明できなかった詳細な部分について解説します。
まず、オイラー線とは「垂心・重心・外心は一直線上に並ぶ」という定理における、その直線のことを言います。発見者である有名な数学者レオンハルト・オイラーに由来するそうです。
これは分解して考えると、
- 垂心の座標を求める(仮定する)
- 重心の座標を求める(仮定する)
- 外心の座標を求める(仮定する)
と段階を踏んだのち、結論として「3点は一直線上に並ぶ」(共線Collinearである)ということが言えればいいわけです。
また、それぞれの点に関しても、
①垂心の場合:
垂心をVとすると
- 対辺BCと垂線ADは垂直に交わる(直交線
Cross verticallyである) - 対辺CAと垂線BEは垂直に交わる(直交線
Cross verticallyである) - 対辺ABと垂線CFは垂直に交わる(直交線
Cross verticallyである) - 点DはBC上にあり、一直線上に並ぶ(共線
Collinearである) - 点EはCA上にあり、一直線上に並ぶ(共線
Collinearである) - 点FはAB上にあり、一直線上に並ぶ(共線
Collinearである) - 点VはAD上にあり、一直線上に並ぶ(共線
Collinearである) - 点VはBE上にあり、一直線上に並ぶ(共線
Collinearである)
②重心の場合:
重心をGとすると
- 点LはBCの中点(中点
Mid pointである) - 点MはCAの中点(中点
Mid pointである) - 点NはABの中点(中点
Mid pointである) - 点GはAL上にあり、一直線上に並ぶ(共線
Collinearである) - 点GはBM上にあり、一直線上に並ぶ(共線
Collinearである)
③外心の場合:
外心をXとすると
- 点LはBCの中点(中点
Mid pointである) - 点MはCAの中点(中点
Mid pointである) - 点NはABの中点(中点
Mid pointである) - 垂直二等分線XLと辺BCは垂直に交わる(直交線
Cross verticallyである) - 垂直二等分線XMと辺CAは垂直に交わる(直交線
Cross verticallyである) - 垂直二等分線XNと辺ABは垂直に交わる(直交線
Cross verticallyである)
と、上記のような関係が各点の性質から判明します。(各点について個別に定理証明したい場合、任意の一つの数式を結論として、それ以外を仮定としてReduceで計算すれば、正しいことがわかるでしょう)
同様にして、
3点についてのすべての数式を仮定とし、
前述した「3点は一直線上に並ぶ」(共線Collinearである)という性質を結論としてReduceで計算すると、見事めでたく簡約した結果が「=0」となり、この定理が正しいということが証明されました………!!
感想とまとめ
本当ならば「けんきうしつ の さがしかた」というタイトルでslis教員への愛を叫ぶ予定だったのですが、急遽主専攻実習の最終発表のフォローアップをすべきと思い、主題を変更させていただきました。また、親愛なるklis16同期のみなさまにおかれましては、1年間の主専攻実習本当にお疲れ様でした………。これからは個々の研究室での活動が主になるかとは思いますが、ぜひ時折お互いに顔を合わせて親交を深めたり、研究テーマについて意見交換したりといったことが行なっていければいいのかなと思います。
ここまで読んでいただきありがとうございました。
追記1
次回、12日目の記事はアマミ( @amaminoclo )くんによる「知識科学の各科目への愛を叫ぶ(仮)」です。
今度はまた毛色の違った主専攻の話が見れそうですよ(?)
乞うご期待!!!!!!!