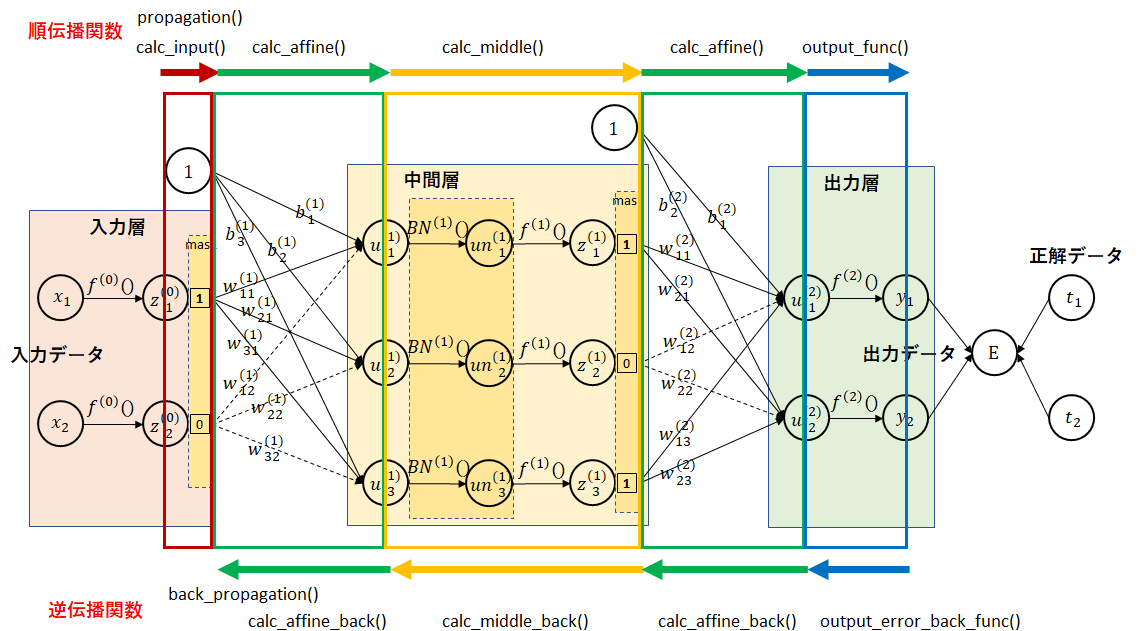
前回は、学習データ正解率が100%に達し、それ以上テストデータ正解率が向上しませんでした。学習データの誤差ではなく、本当のデータ誤差を最小にする正則化について試してみます。
正則化の手法として、早期終了、重み減衰、ドロップアウト、バッチ正規化について、確認してみます。データは、MNISTです。
早期終了
一番簡単な方法が、早期終了です。テストデータの誤差が減少しなくなった際に終了させるというものです。
前回作成した既定値で実行してみます。
# MNISTデータ読み込み
x_train, t_train, x_test, t_test = load_mnist('c:\\mnist\\')
_, _, _, _, train_rate, train_err, test_rate, test_err, total_time = learn("test", x_train, t_train, x_test, t_test)
テストデータの正解率の最大、誤差の最小のエポック数を調べてみます。
print("argmax(test_rate) = " + str(np.argmax(test_rate)) + " max(test_rate) = " + str(np.max(test_rate)))
print("argmax(test_err) = " + str(np.argmin(test_err)) + " min(test_err) = " + str(np.min(test_err)))
16エポック目が誤差が最小でした。
argmax(test_rate) = 34 max(test_rate) = 0.9788
argmax(test_err) = 16 min(test_err) = 0.0716534037059
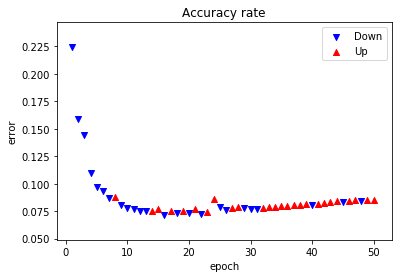
誤差をグラフ化してみます。誤差が減少した場合青▼で、増加した場合赤▲で示します。
import numpy as np
import matplotlib.pyplot as plt
# データ設定
for i in range(50):
if test_err[i] > test_err[i+1]:
x_down = np.append(x_down, i+1)
y_down = np.append(y_down, test_err[i+1])
else:
x_up = np.append(x_up, i+1)
y_up = np.append(y_up, test_err[i+1])
# グラフ表示
plt.scatter(x_down, y_down, label="Down", marker="v", color="blue")
plt.scatter(x_up, y_up, label="Up", marker="^", color="red")
plt.title("Accuracy rate")
plt.xlabel("epoch")
plt.ylabel("error")
plt.legend()
plt.show()
8エポック目で初めて減少しています。32エポック目から8連続減少しています。
どこで終了するかは、パラメータで決めるようです。例えば、3エポック連続で減少で終了とすると、32エポックとなり、31エポック目で打ち切りとします。
ここで、注意が必要な点は、テストデータの結果を利用していることです。未知のデータを予測することを考えると問題があります。学習データの一部を切り出して検証データとすべきです。
早期終了については、過去のデータを保持しておく必要があり、今回は、実装しません。
重み減衰
大きな重みにペナルティを課すものです。
学習は、誤差を最小とするように重み、バイアスを調整することでした。誤差に重みを加えて、誤差+重みを最小とするように学習します。誤差の加え方でいろいろな方法があります。
L1ノルム
すべての重みの絶対値の和を加えます。
\tilde{E} = E + \lambda\sum_{k}\sum_{i}\sum_{j}|w_{ij}^{(k)}|
$ \lambda $は、パラメータです。$ \tilde{E} $が最小となるように学習します。
順伝播
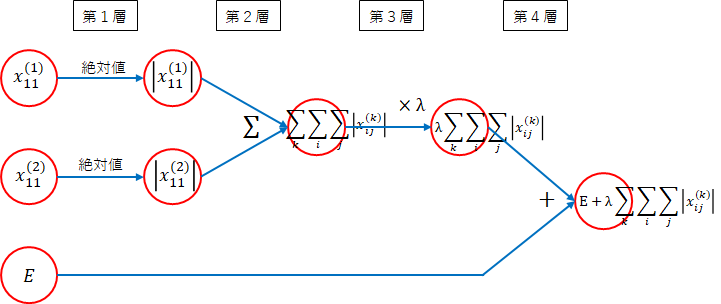
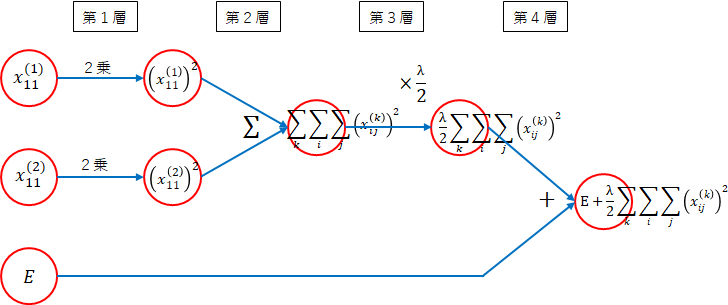
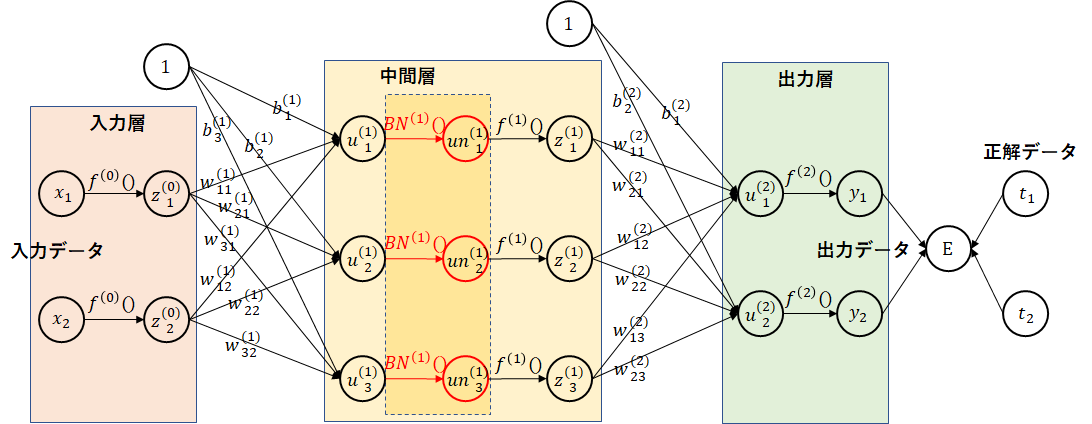
順伝播を考えます。ネットワーク図を描いて考えます。
まずは、$ E $の部分です。簡単のために、重みは、1層目と2層目の$ w_{11}^{(1)} $、$ w_{11}^{(2)} $を対象にします。本来は、すべての重みですが考え方は同じです。
-
第1層
重みの絶対値をとります。 -
第2層
重みの絶対値をすべて加えます。 -
第3層
$ \lambda $を掛けます。 -
第4層
誤差に加えます。
逆伝播
各層の勾配を求めます。
逆伝播を考えるため、まず、前回までに利用した法則を振り返ります。
** 法則1:勾配は、ネットワークの各線の勾配の積となる。**
** 法則2:分岐の場合は、それぞれの勾配の和となる。**
** 法則3:複雑な関数は分解し、法則1、法則2を利用し勾配を求める。**
** ($ + $定数):定数を加えた場合の勾配 $ =1 $**
** ($ \times $定数):定数を掛けた場合の勾配 $ = $ 定数**
** ($ \sum $):$ \sum $の勾配 $ =1 $**
** ($ \times $):2つの変数の掛け算の勾配は、それぞれ逆の変数となる**
** (関数):関数の勾配は、数学の力を借りる**
$ \log(x) $ → $ \frac{1}{x} $、$ \exp(x) $ → $ \exp(x) $、$ \frac{1}{x} $ → $ -\frac{1}{x^2} $、$ \sqrt{x} $ → $ \frac{1}{2\sqrt{x}} $
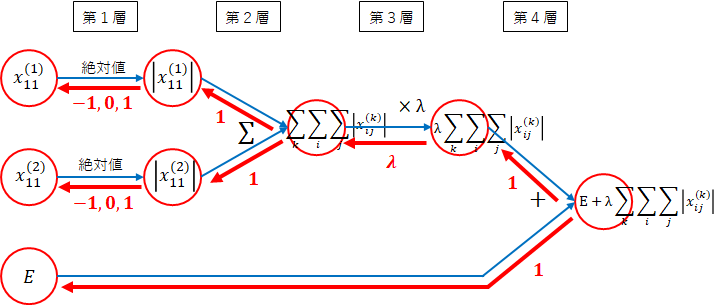
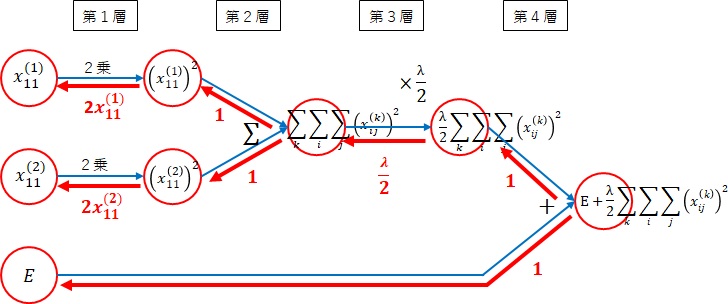
逆伝播のネットワーク図は、次のようになります。
-
第4層
法則3($ \sum $)より$ 1 $になります。 -
第3層
法則3($ \times $定数)より掛けた値、$ \lambda $になります。 -
第2層
法則3($ \sum $)より$ 1 $になります。 -
第1層
絶対値は、以下の式で表せます。
f(x) = |x| = \left\{
\begin{array}{ll}
x & (x \gt 0)\\
0 & (x = 0)\\
-x & (x \lt 0)
\end{array}
\right.
勾配は、以下になります。
f^{'}(x) = \left\{
\begin{array}{ll}
1 & (x \gt 0)\\
0 & (x = 0)\\
-1 & (x \lt 0)
\end{array}
\right.
本来は、$ x=0 $の勾配は不定ですがここでは、$ 0 $とします。
全体の勾配です。
$ E $の方向は、$ \times 1 $なので、今までと変わりはありません。
重み方向は、法則1より、第4層~第1層までの勾配を掛けます。
$ w_{ij}^{(k)} > 0 $の場合
1 \times \lambda \times 1 \times 1 = \lambda
$ w_{ij}^{(k)} = 0 $の場合
1 \times \lambda \times 1 \times 0 = 0
$ w_{ij}^{(k)} < 0 $の場合
1 \times \lambda \times 1 \times -1 = -\lambda
今までの方向と$ \tilde{E} $の方向の分岐になるため、法則2により、今までの勾配と今回の勾配の和になります。
学習は、以下のように行いました。
w = w - \eta E^{'}(w)
L1ノルムを適用すると以下になります。
$ w_{ij}^{(k)} > 0 $の場合
w = w - \eta (E^{'}(w) + \lambda) = w - \eta E^{'}(w) - \eta \lambda
$ \eta \lambda $分、重みを減少させることになります。
$ w_{ij}^{(k)} < 0 $の場合
w = w - \eta (E^{'}(w) - \lambda) = w - \eta E^{'}(w) + \eta \lambda
$ \eta \lambda $分、重みを増加させることになります。重みが負のため、重みの絶対値を小さくする方に働きます。
実装
regularization_paramsに、重み減衰のパラメータを設定します。
regularization_params["weight_decay_func"]に重み減衰の勾配を計算する関数を設定します。後で説明するL2ノルムもありますので、指定できるようにします。
regularization_params["weight_decay_lambda"]に重みをどの程度適用するかの定数を指定します。値が大きいと重みの影響が大きくなり、小さいと重みの影響が小さくなります。
勾配関数は、以下でregularization_params["weight_decay_back_func"]に設定します。
if "weight_decay_func" in regularization_params: # 重み減衰
regularization_params["weight_decay_back_func"] = eval(regularization_params["weight_decay_func"].__name__ + "_back")
- $ \tilde{E} $の計算
全層の絶対値の重みの和を計算し、$ \lambda $を掛けます。
def L1_norm(W, weight_decay_lambda):
r = 0.
for WI in W.values():
r = r + np.sum(np.absolute(WI))
return weight_decay_lambda * r
誤差計算は、error_funcで直接行っていましたが、重み減衰を計算するため、calc_errorからerror_funcを呼び出すようにします。
def calc_error(y, t, W, error_func, regularization_params):
e = error_func(y, t)
if "weight_decay_func" in regularization_params: # 重み減衰対応
e = e + regularization_params["weight_decay_func"](W, regularization_params["weight_decay_lambda"])
return e
- 逆伝播
逆伝播は、1層ごと行います。
def L1_norm_back(W, weight_decay_lambda):
return np.where(W > 0, weight_decay_lambda, np.where(W < 0, -weight_decay_lambda, 0))
アフィン変換の勾配で、重みの勾配を計算していますので、改造します。勾配関数は、regularization_params["weight_decay_back_func"]に格納しています。
def calc_affine_back(du, z, W, b, regularization_params):
dz, dW, db = affine_back(du, z, W, b)
if "weight_decay_func" in regularization_params: # 重み減衰対応
dW = dW + regularization_params["weight_decay_back_func"](W, regularization_params["weight_decay_lambda"])
return dz, dW, db
後は、パラメータの受け渡しの追加、名前を変更した関数の呼び出しを変更します。全体のプログラムは、最後の参考に記載します。
結果
$ \lambda $を変更し実行しました。
# MNISTデータ読み込み
x_train, t_train, x_test, t_test = load_mnist('c:\\mnist\\')
Ws = {}
train_rates = {}
train_errs = {}
test_rates = {}
test_errs = {}
total_times = {}
weight_decay_lambda = [0.1,0.01,0.001,0.0001,0.00001,0.000001]
for lmd in weight_decay_lambda:
name = "L1 " + str(lmd)
regularization_params = {"weight_decay_func":L1_norm, "weight_decay_lambda":lmd}
_, _, Ws[name], _, train_rates[name], train_errs[name], test_rates[name], test_errs[name], total_times[name] = learn(
name, x_train, t_train, x_test, t_test, regularization_params=regularization_params)
結果を表にします。
今回からテスト正解率の最高値とその時のエポック数も含めます。
- 学習正解:50エポック実行後の学習データの正解率(%)
- テスト正解:50エポック実行後のテストデータの正解率(%)
- TS95%:テストデータの正解率が95%に達したエポック数
- TS97%:テストデータの正解率が97%に達したエポック数
- TS98%:テストデータの正解率が98%に達したエポック数
- TS最高:テストデータの最高正解率(%)
- エポック:テストデータの最高正解率時のエポック数
参考までに、L1ノルムを適用しない場合も載せます。
| $ \lambda $ | 学習正解 | テスト正解 | TS95% | TS97% | TS98% | TS最高 | エポック |
|---|---|---|---|---|---|---|---|
| 0.1 | 11.24 | 11.35 | - | - | - | 11.35 | 1 |
| 0.01 | 84.03 | 84.46 | - | - | - | 85.28 | 5 |
| 0.001 | 95.61 | 95.45 | 27 | - | - | 95.66 | 39 |
| 0.0001 | 99.16 | 97.82 | 2 | 5 | 32 | 98.08 | 39 |
| 0.00001 | 100.00 | 97.92 | 2 | 5 | 45 | 98.01 | 45 |
| 0.000001 | 100.00 | 97.94 | 2 | 5 | - | 97.96 | 39 |
| (参考) | 100.00 | 97.85 | 2 | 5 | - | 97.88 | 34 |
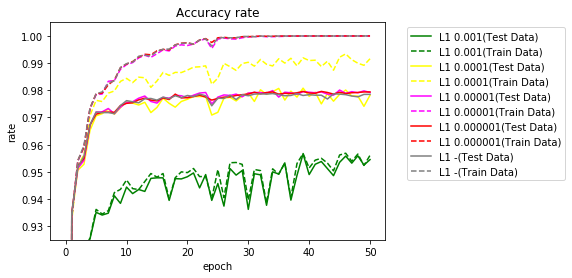
L1ノルムを適用した場合、若干よくなりました。$ \lambda $が大きい場合は、学習データとテストデータの正解率がほぼ同じになりました。
$ \lambda $が小さくなるとほぼL1ノルムを適用しない場合と同じになります。
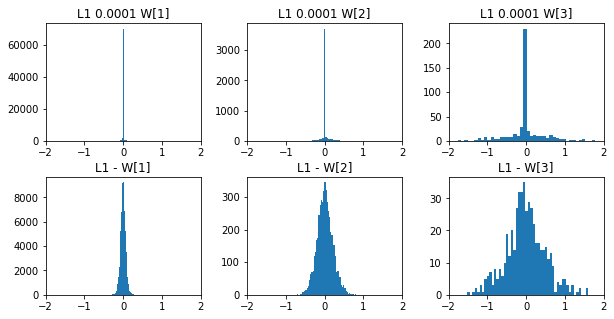
L1ノルムを適用した場合と適用しない場合の50エポック後の重みをヒストグラムで比較してみます。一目瞭然ですね。
L2ノルム
重みの二乗和に$ \frac{1}{2} $を掛けます。
\tilde{E} = E + \frac{\lambda}{2}\sum_{k}\sum_{i}\sum_{j}(w_{ij}^{(k)})^2
$ \lambda $は、パラメータです。$ \tilde{E} $が最小となるように学習します。
順伝播
L1ノルムと同様にネットワーク図を描いて考えます。
-
第1層
重みを2乗します。 -
第2層
重みの2乗をすべて加えます。 -
第3層
$ \frac{\lambda}{2} $を掛けます。 -
第4層
誤差に加えます。
逆伝播
各層の勾配を求めます。
逆伝播のネットワーク図は、次のようになります。
-
第4層
法則3($ \sum $)より$ 1 $になります。 -
第3層
法則3($ \times $定数)より掛けた値、$ \frac{\lambda}{2} $になります。 -
第2層
法則3($ \sum $)より$ 1 $になります。 -
第1層
2乗は、以下の式で表せます。
\begin{align}
f(x) &= x^2\\
f^{'}(x) &= 2x
\end{align}
重みに2を掛けた値になります。
全体の勾配です。
$ E $の方向は、$ \times 1 $なので、今までと変わりはありません。
重み方向は、法則1より、第4層~第1層までの勾配を掛けます。
1 \times \frac{\lambda}{2} \times 1 \times 2w_{ij}^{(k)} = \lambda w_{ij}^{(k)}
今までの方向と$ \tilde{E} $の方向の分岐になるため、法則2により、今までの勾配と今回の勾配の和になります。
学習は、以下のように行いました。
w = w - \eta E^{'}(w)
L2ノルムを適用すると以下になります。
w = w - \eta (E^{'}(w) + \lambda w_{ij}^{(k)}) = w - \eta E^{'}(w) - \eta \lambda w_{ij}^{(k)}
$ w_{ij}^{(k)} > 0 $の場合
$ \eta \lambda w_{ij}^{(k)} $分、重みを減少させることになります。
$ w_{ij}^{(k)} < 0 $の場合
$ w_{ij}^{(k)} $が負のため、$ \eta \lambda w_{ij}^{(k)} $分、重みを増加させることになります。
実装
L1ノルムと同様に実装します。
- $ \tilde{E} $の計算
全層の2乗の重みの和を計算し、$ \frac{\lambda}{2} $を掛けます。
def L2_norm(W, weight_decay_lambda):
r = 0.
for WI in W.values():
r = r + np.sum(WI**2)
return (weight_decay_lambda * r)/2
- 逆伝播
逆伝播は、1層ごと行います。$ \lambda $に重みを掛ければよいのでした。
def L2_norm_back(W, weight_decay_lambda):
return weight_decay_lambda * W
結果
$ \lambda $を変更し実行しました。
# MNISTデータ読み込み
x_train, t_train, x_test, t_test = load_mnist('c:\\mnist\\')
Ws = {}
train_rates = {}
train_errs = {}
test_rates = {}
test_errs = {}
total_times = {}
weight_decay_lambda = [0.1,0.01,0.001,0.0001,0.00001,0.000001]
for lmd in weight_decay_lambda:
name = "L2 " + str(lmd)
regularization_params = {"weight_decay_func":L2_norm, "weight_decay_lambda":lmd}
_, _, Ws[name], _, train_rates[name], train_errs[name], test_rates[name], test_errs[name], total_times[name] = learn(
name, x_train, t_train, x_test, t_test, regularization_params=regularization_params)
結果を表にします。
参考までに、L2ノルムを適用しない場合も載せます。
| $ \lambda $ | 学習正解 | テスト正解 | TS95% | TS97% | TS98% | TS最高 | エポック |
|---|---|---|---|---|---|---|---|
| 0.1 | 78.90 | 79.55 | - | - | - | 82.55 | 25 |
| 0.01 | 95.26 | 95.39 | 19 | - | - | 95.39 | 50 |
| 0.001 | 99.40 | 98.02 | 3 | 6 | 32 | 98.24 | 45 |
| 0.0001 | 100.00 | 98.01 | 2 | 5 | 50 | 98.01 | 50 |
| 0.00001 | 100.00 | 97.89 | 2 | 5 | - | 97.93 | 34 |
| 0.000001 | 100.00 | 97.97 | 2 | 5 | - | 97.97 | 50 |
| (参考) | 100.00 | 97.85 | 2 | 5 | - | 97.88 | 34 |
L2ノルムを適用した場合、若干よくなりました。$ \lambda $が大きい場合は、学習データとテストデータの正解率がほぼ同じになりました。
$ \lambda $が小さくなるとほぼL2ノルムを適用しない場合と同じになります。
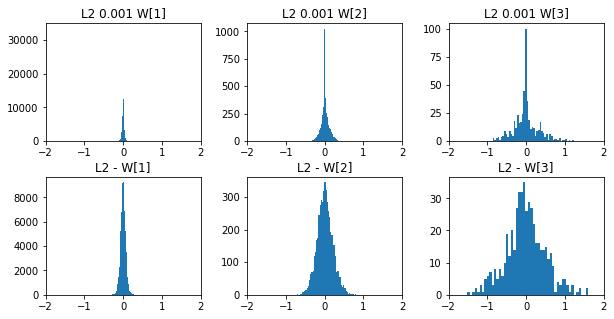
L2ノルムを適用した場合と適用しない場合の50エポック後の重みをヒストグラムで比較してみます。やはり、重みの絶対値は小さくなっています。
判明したこと
重み減衰を適用すると$ \lambda $が大きいと学習データとテストデータの正解率の差がほとんどなくなりました。ただし、正解率はよくありません。$ \lambda $を小さくするとほとんど重み減衰の効果がなくなります。$ \lambda $を適度に選べば正解率が向上しましたが、今回確認したMNISTでは、ほんのわずかでした。
ドロップアウト
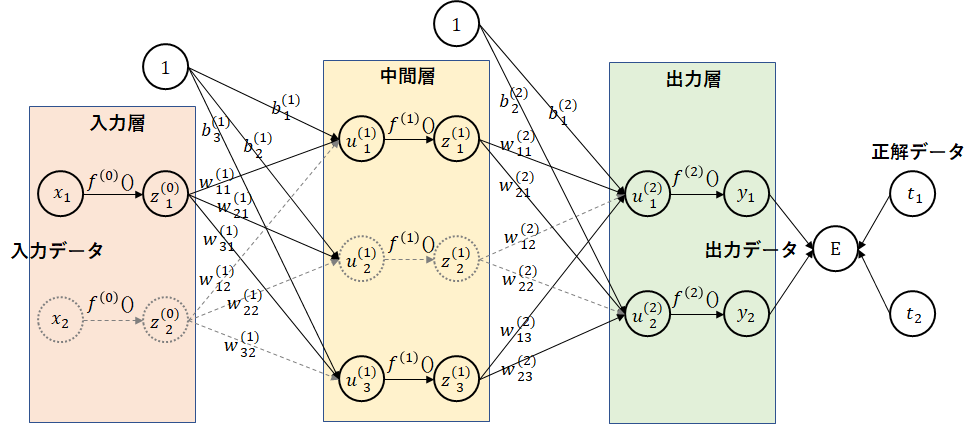
入力層のデータ、中間層のノードを一定の割合で存在しないことにする方法がドロップアウトです。ドロップアウトしたデータは学習で利用されません。どのデータをドロップアウトさせるかは、バッチごとにランダムに決定します。
順伝播
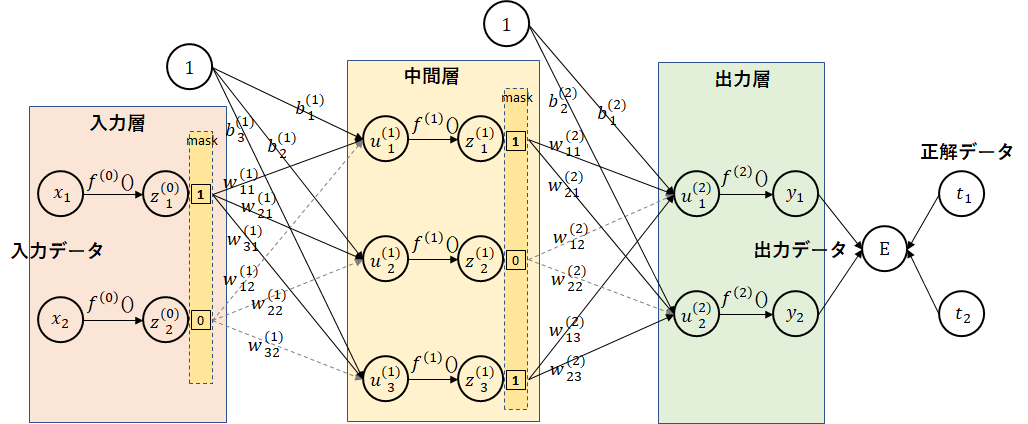
入力データ、活性化関数後のデータをマスクすることを考えます。マスクとして、ドロップアウトするノードには、$ 0 $を、ドロップアウトしないノードには、$ 1 $を与えます。データにマスクを掛けることにより、ドロップアウトするデータは、$ 0 $となり、データが存在しないことと同じになります。ドロップアウトしないデータは、元の値のままです。
逆伝播
ドロップアウトするデータには、$ 0 $を、ドロップアウトしないデータには、$ 1 $を掛けました。法則3($ \times $定数)よりそのままの値を掛ければよいことになります。順伝播同様に、マスクをかければよいことになります。
実装
入力層のドロップアウト率と中間層のドロップアウト率は、別々に指定します。
入力層のドロップアウト率は、regularization_params["dropout_input_ratio"]で与えます。
中間層のドロップアウト率は、regularization_params["dropout_middle_ratio"]で与えます。
学習時は、マスクを使用しますが、テストデータの評価時にはマスクを利用しません。学習時は、ドロップアウト率を掛けた割合のデータのみ利用しますが、評価時には全データを利用します。そのため、評価時には、データにドロップアウト率を掛けて調整を行います。
- マスク生成
各層のマスクを生成します。
# ドロップアウト
def set_dropout_mask(d, regularization_params):
mask = {}
if "dropout_input_ratio" in regularization_params:
mask[0] = np.zeros(d[0])
ratio = regularization_params["dropout_input_ratio"]
mask_idx = np.random.choice(d[0], round(ratio*d[0]), replace=False) # 通すindexの配列
mask[0][mask_idx] = 1
if "dropout_middle_ratio" in regularization_params:
for i in range(1, len(d)-1):
mask[i] = np.zeros(d[i])
ratio = regularization_params["dropout_middle_ratio"]
mask_idx = np.random.choice(d[i], round(ratio*d[i]), replace=False) # 通すindexの配列
mask[i][mask_idx] = 1
return mask
- 順伝播
順伝播は、マスクをかければよいのでした。
def dropout(z, mask):
return z * mask
入力データに対しても処理が必要です。
入力層のドロップアウト率が指定されている場合は、マスクをかけます。
評価時には、ドロップアウト率を掛けて調整を行います。
# 入力計算
def calc_input(x, regularization_params, dropout_mask):
if "dropout_input_ratio" in regularization_params:
if dropout_mask is not None:
x = dropout(x, dropout_mask)
else:
x = x * regularization_params["dropout_input_ratio"]
return x
中間層のマスク処理は、活性化関数による計算時に行いました。
評価時には、ドロップアウト率を掛けて調整しています。
# 活性化関数計算
def calc_middle(u, middle_func, middle_params, regularization_params, dropout_mask):
z = middle_func(u, middle_params)
if "dropout_middle_ratio" in regularization_params:
if dropout_mask is not None:
z = dropout(z, dropout_mask)
else:
z = z * regularization_params["dropout_middle_ratio"]
return z
- 逆伝播
順伝播も、マスクをかければよいのでした。
def dropout_back(dz, mask):
return dz * mask
活性化関数による勾配計算時にマスク対応を行いました。
# 活性化関数勾配計算
def calc_middle_back(dz, u, z, middle_back_func, middle_params, regularization_params, dropout_mask):
if dropout_mask is not None:
dz = dropout_back(dz, dropout_mask)
return middle_back_func(dz, u, z, middle_params)
結果
入力層、中間層のドロップアウト率をそれぞれ0.5~1.0に変更し実行しました。
# MNISTデータ読み込み
x_train, t_train, x_test, t_test = load_mnist('c:\\mnist\\')
train_rates = {}
train_errs = {}
test_rates = {}
test_errs = {}
total_times = {}
dropout_middle_ratio = [0.5,0.6,0.7,0.8,0.9,1.0]
dropout_input_ratio = [1.0,0.9,0.8,0.7,0.6,0.5]
for input_ratio in dropout_input_ratio:
for middle_ratio in dropout_middle_ratio:
name = "dropout_input_ratio=" + str(input_ratio) + ",dropout_middle_ratio=" + str(middle_ratio)
regularization_params = {"dropout_input_ratio":input_ratio, "dropout_middle_ratio":middle_ratio}
_, _, _, _, train_rates[name], train_errs[name], test_rates[name], test_errs[name], total_times[name] = learn(
name, x_train, t_train, x_test, t_test, regularization_params=regularization_params)
結果を表にします。
過学習が抑制されることは想定していましたが、入力層のドロップアウトで非常に良い結果が得られました。
| 入力層率 | 中間層率 | 学習正解 | テスト正解 | TS95% | TS97% | TS98% | TS最高 | エポック |
|---|---|---|---|---|---|---|---|---|
| 1.0 | 0.5 | 98.15 | 96.96 | 10 | 40 | - | 97.09 | 45 |
| 1.0 | 0.6 | 98.82 | 97.48 | 6 | 20 | - | 97.67 | 43 |
| 1.0 | 0.7 | 99.24 | 97.80 | 5 | 13 | - | 97.80 | 50 |
| 1.0 | 0.8 | 99.64 | 98.10 | 3 | 10 | 38 | 98.10 | 50 |
| 1.0 | 0.9 | 99.86 | 97.99 | 3 | 8 | 34 | 98.11 | 40 |
| 1.0 | 1.0 | 100.00 | 97.89 | 2 | 5 | 48 | 98.00 | 48 |
| 0.9 | 0.5 | 97.80 | 97.08 | 10 | 42 | - | 97.17 | 47 |
| 0.9 | 0.6 | 98.47 | 97.48 | 7 | 22 | - | 97.57 | 43 |
| 0.9 | 0.7 | 98.94 | 97.71 | 5 | 16 | - | 97.86 | 49 |
| 0.9 | 0.8 | 99.43 | 97.98 | 4 | 10 | 34 | 98.05 | 34 |
| 0.9 | 0.9 | 99.71 | 98.18 | 3 | 8 | 26 | 98.25 | 42 |
| 0.9 | 1.0 | 99.93 | 98.11 | 2 | 6 | 18 | 98.26 | 36 |
| 0.8 | 0.5 | 97.40 | 96.86 | 13 | - | - | 96.95 | 42 |
| 0.8 | 0.6 | 98.16 | 97.34 | 8 | 25 | - | 97.49 | 41 |
| 0.8 | 0.7 | 98.66 | 97.74 | 6 | 16 | - | 97.78 | 49 |
| 0.8 | 0.8 | 99.03 | 97.92 | 4 | 11 | - | 97.99 | 47 |
| 0.8 | 0.9 | 99.42 | 98.27 | 3 | 10 | 28 | 98.27 | 50 |
| 0.8 | 1.0 | 99.75 | 98.25 | 3 | 6 | 19 | 98.38 | 41 |
| 0.7 | 0.5 | 97.15 | 96.78 | 15 | - | - | 96.79 | 44 |
| 0.7 | 0.6 | 97.84 | 97.34 | 9 | 26 | - | 97.34 | 50 |
| 0.7 | 0.7 | 98.34 | 97.51 | 6 | 22 | - | 97.60 | 49 |
| 0.7 | 0.8 | 98.70 | 97.77 | 4 | 14 | - | 97.80 | 38 |
| 0.7 | 0.9 | 99.16 | 98.13 | 4 | 10 | 31 | 98.20 | 49 |
| 0.7 | 1.0 | 99.56 | 98.32 | 3 | 8 | 20 | 98.42 | 48 |
| 0.6 | 0.5 | 96.86 | 96.46 | 17 | - | - | 96.63 | 49 |
| 0.6 | 0.6 | 97.45 | 97.01 | 11 | 40 | - | 97.08 | 49 |
| 0.6 | 0.7 | 97.96 | 97.24 | 7 | 27 | - | 97.36 | 48 |
| 0.6 | 0.8 | 98.37 | 97.50 | 6 | 18 | - | 97.65 | 49 |
| 0.6 | 0.9 | 98.86 | 98.15 | 4 | 11 | 40 | 98.15 | 50 |
| 0.6 | 1.0 | 99.20 | 98.15 | 4 | 8 | 22 | 98.54 | 44 |
| 0.5 | 0.5 | 96.31 | 95.95 | 20 | - | - | 96.12 | 48 |
| 0.5 | 0.6 | 96.94 | 96.46 | 15 | - | - | 96.64 | 46 |
| 0.5 | 0.7 | 97.54 | 96.91 | 10 | 42 | - | 97.10 | 46 |
| 0.5 | 0.8 | 97.97 | 97.16 | 6 | 26 | - | 97.39 | 46 |
| 0.5 | 0.9 | 98.48 | 97.87 | 6 | 17 | - | 97.92 | 48 |
| 0.5 | 1.0 | 98.83 | 98.09 | 6 | 11 | 30 | 98.37 | 49 |
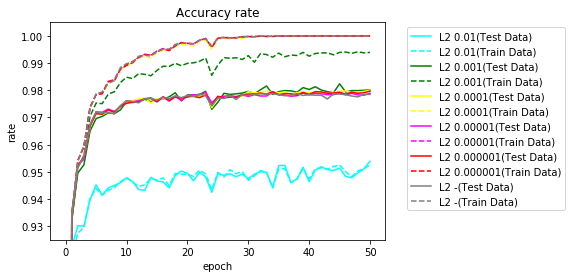
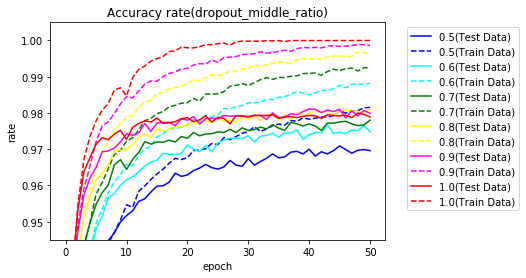
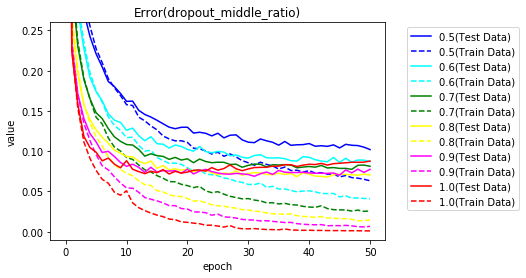
まずは、入力層をドロップアウトなし(1.0)で、中間層のドロップアウト率を0.5~1.0として実行した正解率をグラフ化します。
誤差のグラフです。
ドロップアウトを行うと学習データに対する正解率が100%に達せず過学習がおさえられていることがわかります。
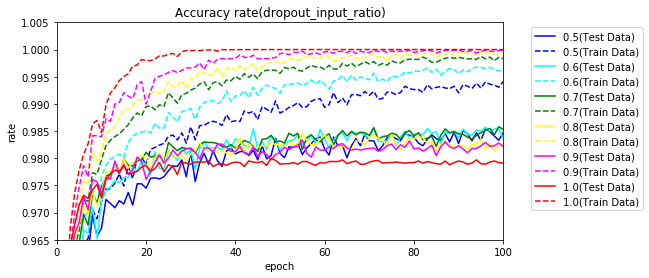
次に、中間層がドロップアウトなし(1.0)で、入力層をドロップアウトさせた場合です。過学習が発生せず学習が進んでいます。
50エポックまで実行していますが、100エポックまで実行してみます。
| 入力層率 | 中間層率 | 学習正解 | テスト正解 | TS95% | TS97% | TS98% | TS最高 | エポック |
|---|---|---|---|---|---|---|---|---|
| 0.5 | 1.0 | 99.41 | 98.47 | 6 | 11 | 30 | 98.54 | 96 |
| 0.6 | 1.0 | 99.64 | 98.37 | 4 | 8 | 22 | 98.57 | 71 |
| 0.7 | 1.0 | 99.83 | 98.53 | 3 | 8 | 20 | 98.58 | 99 |
| 0.8 | 1.0 | 99.93 | 98.27 | 3 | 6 | 19 | 98.46 | 55 |
| 0.9 | 1.0 | 99.98 | 98.22 | 2 | 6 | 18 | 98.34 | 55 |
| 1.0 | 1.0 | 100.00 | 97.91 | 2 | 5 | 48 | 98.00 | 48 |
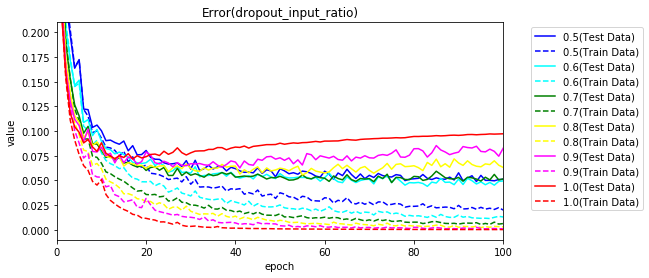
グラフ化してみます。
誤差もグラフ化します。
判明したこと
ドロップアウトを行うと過学習が抑制されることがわかりました。MNISTでは、特に、入力層をドロップアウトさせると非常に良い結果が得られました。
バッチ正規化
前回、入力層でデータを正規化することにより学習が早く進むことを確認しました。正規化を中間層にも取り込む手法が、バッチ正規化です。
中間層の活性化関数の実行前に、データの正規化を行います。
正規化(標準化)
正規化では、平均を0、分散を1とするデータに変換します。
バッチのデータ数が$ m $の場合の正規化方法は、次の通りです。
- 平均
\mu = \frac{1}{m}\sum_{k=1}^{m}x_k
- 分散
\sigma^2 = \frac{1}{m}\sum_{k=1}^{m}(x_k - \mu)^2
- 正規化
\hat{x_i} = \frac{x_i - \mu}{\sqrt{\sigma^2}}
注意すべき点としては、データ系列ごとに平均、分散を求めることです。
(参考)
- 正規化後の平均
\begin{align}
\frac{1}{m}\sum_{k=1}^m\hat{x_k} &= \frac{1}{m}\sum_{k=1}^m\frac{x_k - \mu}{\sqrt{\sigma^2}}\\
&= \frac{1}{m}\frac{x_1+x_2+\cdots+x_m-m\mu}{\sqrt{\sigma^2}}\\
&= \frac{\frac{x_1+x_2+\cdots+x_m}{m}-\mu}{\sqrt{\sigma^2}}\\
&= \frac{\mu-\mu}{\sqrt{\sigma^2}}\\
&= 0
\end{align}
- 正規化後の分散
\begin{align}
\frac{1}{m}\sum_{k=1}^{m}(\hat{x_k} - \mu_{\hat{x}})^2 &= \frac{1}{m}\sum_{k=1}^{m}(\frac{x_k - \mu}{\sqrt{\sigma^2}} - 0)^2\\
&= \frac{1}{m}\sum_{k=1}^{m}\frac{(x_k-\mu)^2}{\sigma^2}\\
&= \frac{1}{\sigma^2}\frac{1}{m}\sum_{k=1}^{m}(x_k-\mu)^2\\
&= \frac{1}{\sigma^2}\sigma^2\\
&= 1
\end{align}
順伝播
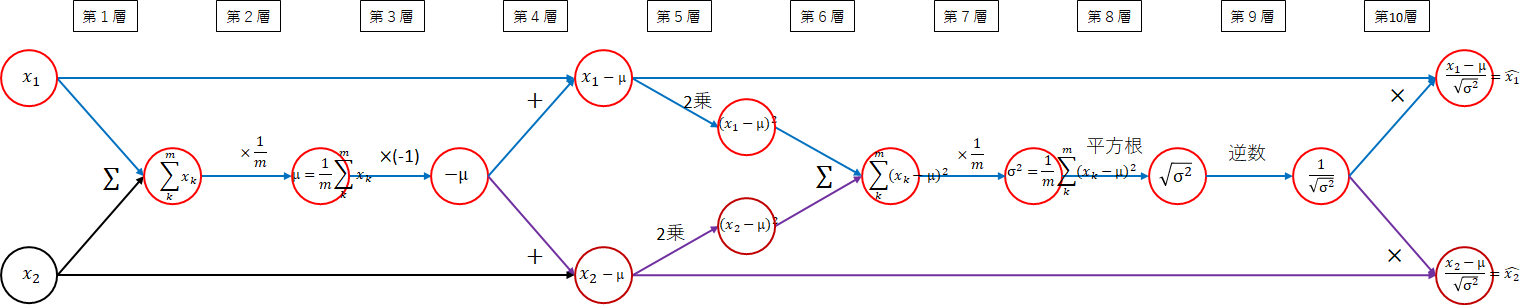
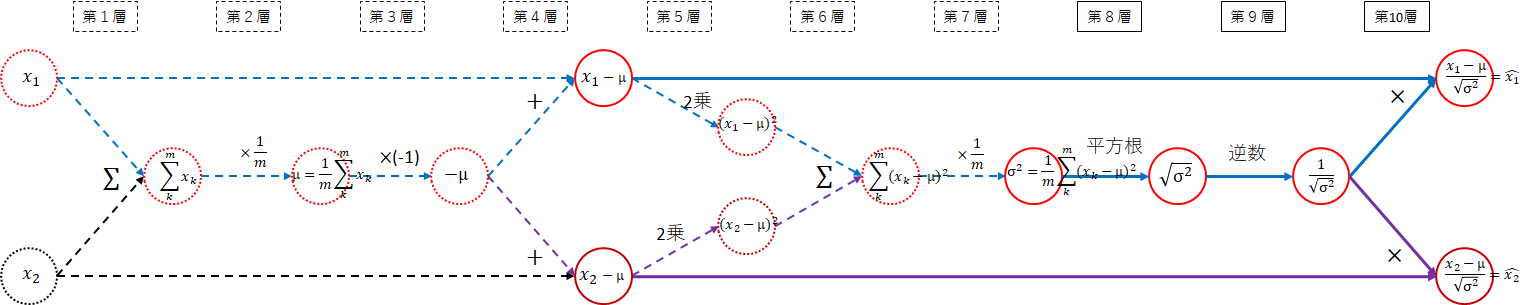
順伝播のネットワーク図を以下に示します。ネットワークをわかりやすくするため、$ m=2 $の図にしています。
10階層にもおよぶ巨大なネットワーク図になりました。平均、分散、正規化に分割して考えます。
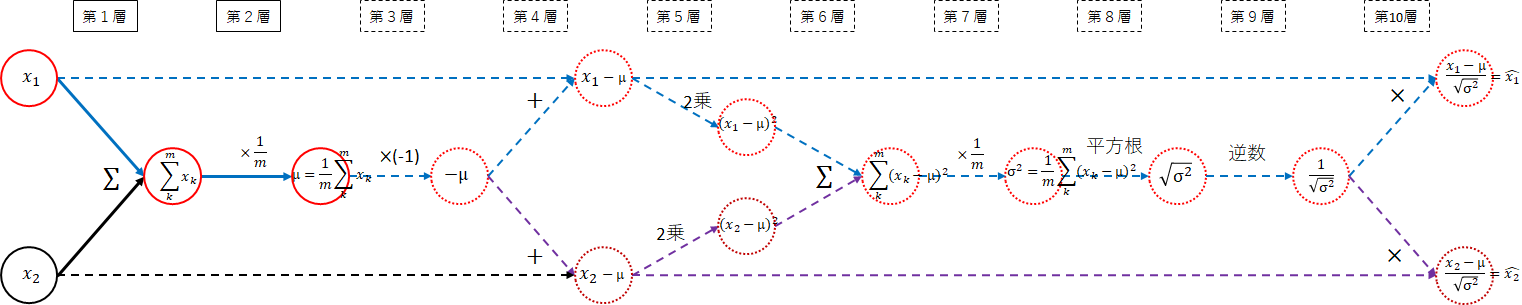
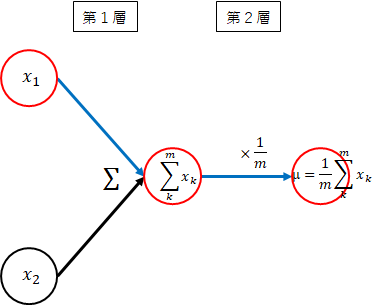
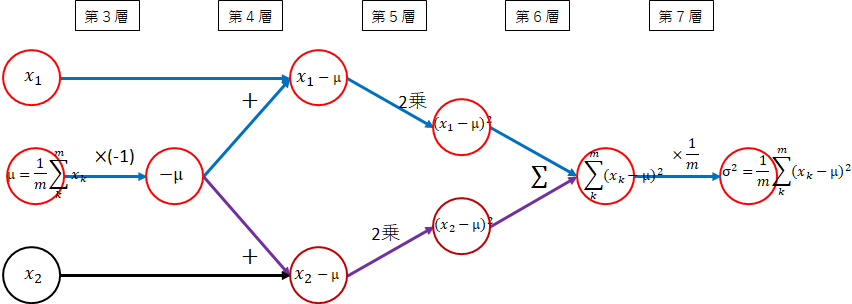
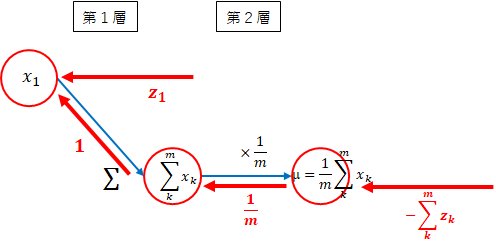
平均
\mu = \frac{1}{m}\sum_{k=1}^{m}x_k
以下のネットワーク図の実線が平均の部分になります。
-
(第1層) $x_i$ → $ \sum_{k=1}^{m}x_k $
各データの和を取ります。 -
(第2層) $ \sum_{k=1}^{m}x_k $ → $ \frac{1}{m}\sum_{k=1}^{m}x_k $
和を$ \frac{1}{m} $します。すなわち、$ \frac{1}{m} $を掛けます。
以下になりました。
平均は、簡単ですね。平均を$ \mu $とします。
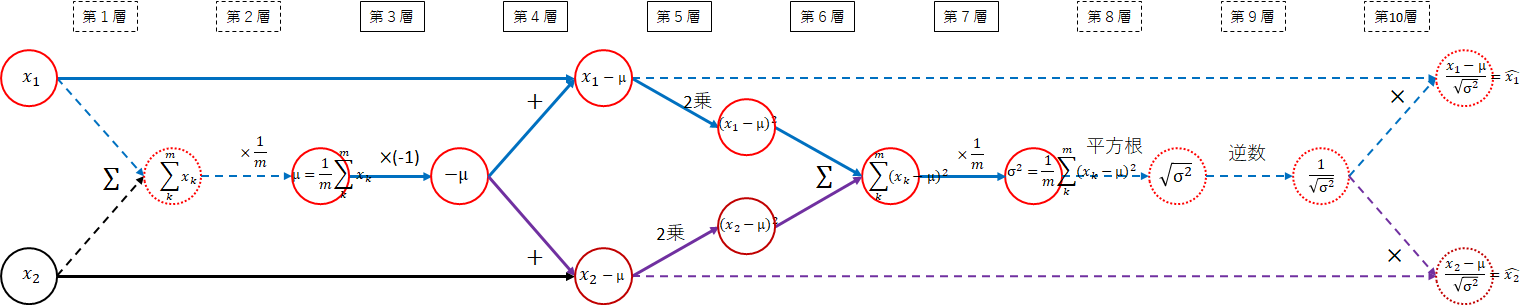
分散
\sigma^2 = \frac{1}{m}\sum_{k=1}^{m}(x_k - \mu)^2
以下のネットワーク図の実線が分散の部分になります。
3~7層に渡り少し複雑です。
-
(3層) $ \mu $ → $ - \mu $
$ x_i $からマイナスする必要があるため、$ -1 $を掛けます。 -
(4層) $ - \mu $ → $ x_i - \mu $
$ x_i $と$ -\mu $を加えます。 -
(5層) $ x_i - \mu $ → $ (x_i - \mu)^2 $
2乗します。 -
(6層) $ (x_i - \mu)^2 $ → $ \sum_{k=1}^{m}(x_k - \mu)^2 $
各データの和を取ります。 -
(7層) $ \sum_{k=1}^{m}(x_k - \mu)^2 $ → $ \frac{1}{m}\sum_{k=1}^{m}(x_k - \mu)^2 $
和を$ \frac{1}{m} $します。すなわち、$ \frac{1}{m} $を掛けます。
以下になりました。
平均を$ \sigma^2 $とします。
正規化
\hat{x_i} = \frac{x_i - \mu}{\sqrt{\sigma^2}}
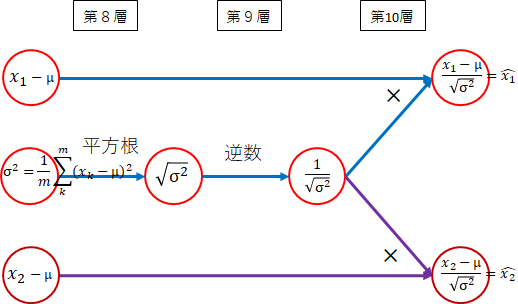
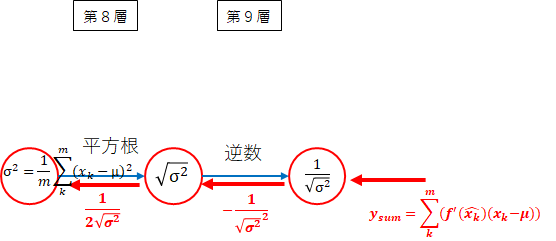
最後は、正規化部分です。実線の部分に対応します。
-
(8層) $ \sigma^2 $ → $ \sqrt{\sigma^2} $
分散の平方根を取ります。 -
(9層) $ \sqrt{\sigma^2} $ → $ \frac{1}{\sqrt{\sigma^2}} $
逆数を取ります。 -
(10層) $ \frac{1}{\sqrt{\sigma^2}} $ → $ \frac{x_i - \mu}{\sqrt{\sigma^2}} $
第4層で求めた$ x_i - \mu $と掛けます。
以下になります。
全体では、以下になります。
ひとつひとつ順番に考えていけば難しくありません。逆伝播を考えるため必要ですので付いて来てください。
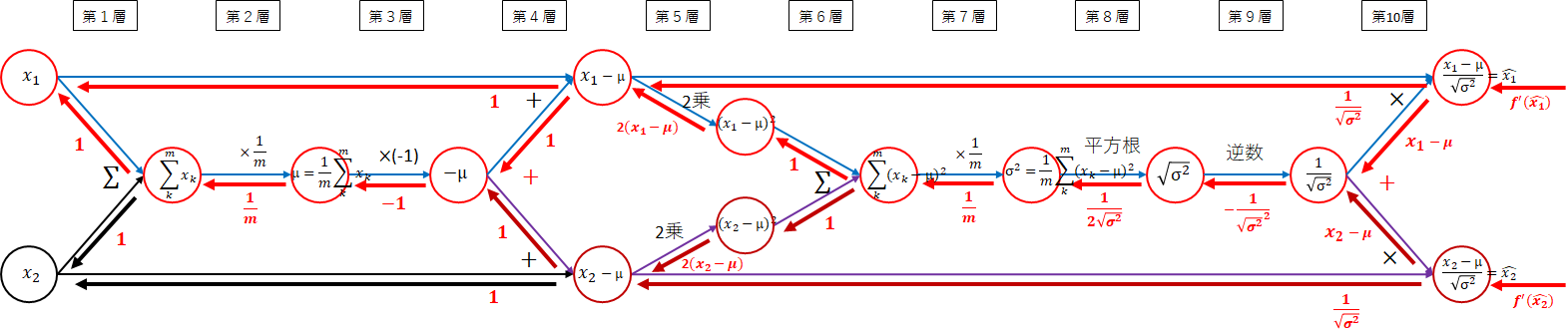
逆伝播
逆伝播を考えるため、法則を再掲します。
** 法則1:勾配は、ネットワークの各線の勾配の積となる。**
** 法則2:分岐の場合は、それぞれの勾配の和となる。**
** 法則3:複雑な関数は分解し、法則1、法則2を利用し勾配を求める。**
** ($ + $定数):定数を加えた場合の勾配 $ =1 $**
** ($ \times $定数):定数を掛けた場合の勾配 $ = $ 定数**
** ($ \sum $):$ \sum $の勾配 $ =1 $**
** ($ \times $):2つの変数の掛け算の勾配は、それぞれ逆の変数となる**
** (関数):関数の勾配は、数学の力を借りる**
$ \log(x) $ → $ \frac{1}{x} $、$ \exp(x) $ → $ \exp(x) $、$ \frac{1}{x} $ → $ -\frac{1}{x^2} $、$ \sqrt{x} $ → $ \frac{1}{2\sqrt{x}} $
今回も法則を利用しながら逆伝播を求めていきます。
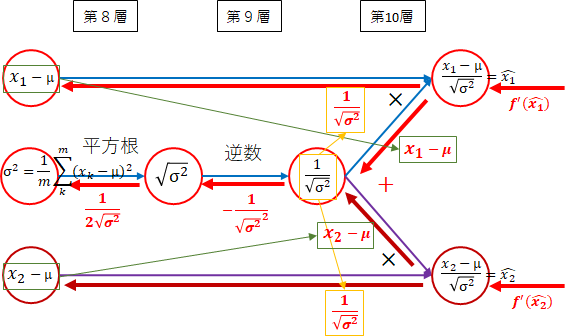
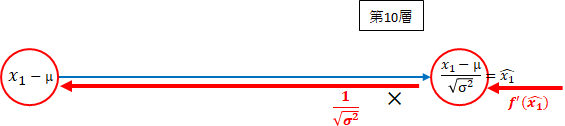
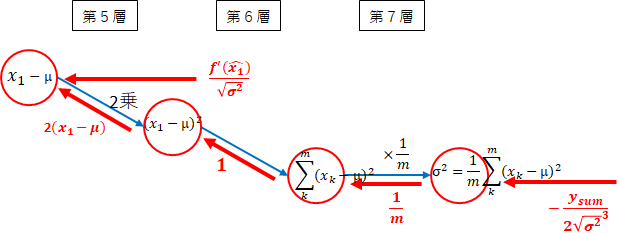
正規化
各層の勾配を計算します。
-
第10層 $ \times $
掛け算は、法則3($ \times $)より、それぞれ逆になります。
$ x_i - \mu $側は、$ \frac{1}{\sqrt{\sigma^2}} $、$ \frac{1}{\sqrt{\sigma^2}} $側は、$ x_i - \mu $になります。 -
第9層 逆数
法則3(関数)より、逆数の勾配は、$ -\frac{1}{x^2} $です。ここでは、$ x $が$ \sqrt{\sigma^2} $のため、$ -\frac{1}{\sqrt{\sigma^2}^2} $となります。 -
第8層 平方根
平方根も法則3(関数)です。平方根の勾配は、$ \frac{1}{2\sqrt{x}} $です。$ x $が$ \sigma^2 $のため、$ \frac{1}{2\sqrt{\sigma^2}} $となります。 -
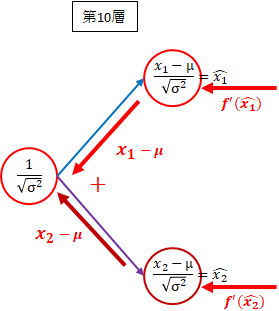
全体の勾配
正規化部分の全体の勾配を求めます。全体の勾配を求めるに際し、第10層への入力が必要となります。ここでは、$ f^{'}(\hat{x_i}) $とします。
3つの部分に分けて考えます。 -
第10層 $ x_1 - \mu $方向
後ろから順番に掛けます。
f^{'}(\hat{x_1}) \times \frac{1}{\sqrt{\sigma^2}} = \frac{f^{'}(\hat{x_1})}{\sqrt{\sigma^2}}
- 第10層 $ \frac{1}{\sqrt{\sigma^2}} $方向
それぞれ後ろから順番に掛け、足し合わせます。
(f^{'}(\hat{x_1}) \times (x_1 - \mu)) + (f^{'}(\hat{x_2}) \times (x_2 - \mu))
一般には、以下になります。
\sum_{k=1}^m(f^{'}(\hat{x_k}) (x_k - \mu))
これを$ y_{sum} $とします。
- 第9層~第8層 $ \sigma^2 $ 方向
後ろから掛けます。
y_{sum} \times -\frac{1}{\sqrt{\sigma^2}^2} \times \frac{1}{2\sqrt{\sigma^2}} = -\frac{y_{sum}}{2\sqrt{\sigma^2}^3}
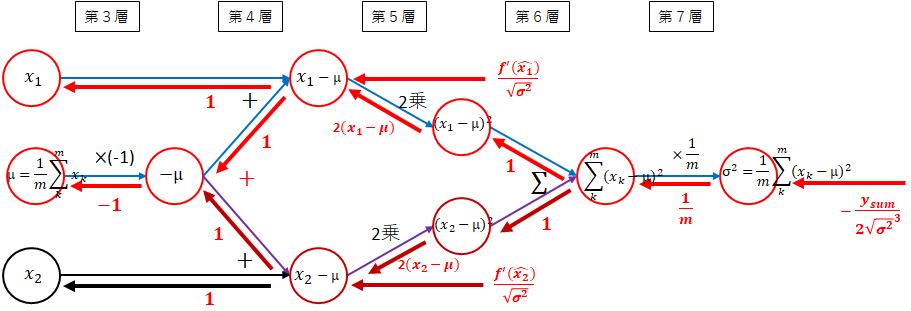
分散
各層の勾配を計算します。
-
第7層 $ \times \frac{1}{m} $
法則3($ \times $定数)より、掛けた値$ \frac{1}{m} $となります。 -
第6層 $ \sum $
法則3($ \sum $)より、$ 1 $となります。 -
第5層 $ 2乗 $
2乗の勾配は、$ 2x $ですので、今回の場合は、$ 2(x_1 - \mu) $です。 -
第4層 $ + $
足し算なので勾配は、$ 1 $になります。 -
第3層 $ \times (-1) $
法則3($ \times $定数)より、掛けた値$ -1 $となります。 -
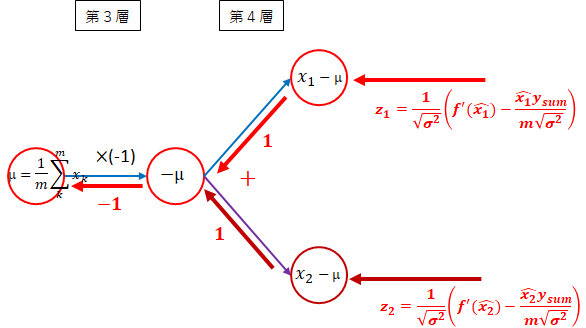
全体の勾配
分散部分の全体の勾配を求めます。全体の勾配を求めるに際し、正規化で求めた勾配を利用します。
3つの部分に分けて考えます。 -
第7層~第5層 $ x_1 - \mu $方向
$ x_1 - \mu $は、2方向から矢印が伸びていますので、法則2により両方の矢印を加えます。
\frac{f^{'}(\hat{x_1})}{\sqrt{\sigma^2}} + ( -\frac{y_{sum}}{2\sqrt{\sigma^2}^3} \times \frac{1}{m} \times 1 \times 2(x_1 - \mu))\\
= \frac{f^{'}(\hat{x_1})}{\sqrt{\sigma^2}} - \frac{y_{sum}\times 2(x_1 - \mu)}{2m\sqrt{\sigma^2}^3}\\
= \frac{1}{\sqrt{\sigma^2}}(f^{'}(\hat{x_1})-\frac{y_{sum}}{m\sqrt{\sigma^2}}\frac{x_1 - \mu}{\sqrt{\sigma^2}})
$ \hat{x_1} = \frac{x_1 - \mu}{\sqrt{\sigma^2}} $でした。
よって、以下となります。
\frac{1}{\sqrt{\sigma^2}}(f^{'}(\hat{x_1})-\frac{\hat{x_1}y_{sum}}{m\sqrt{\sigma^2}})
これを$ z_1 $とします。
- 第4層 $ x_1 $方向
1 \times z_1 = z_1
- 第4層~第3層 $ \mu $方向
法則2により分岐は足します。
((z_1 \times 1) + (z_2 \times 1)) \times -1 = -(z_1 + z_2)
一般的には以下となります。
-\sum_{k=1}^mz_k
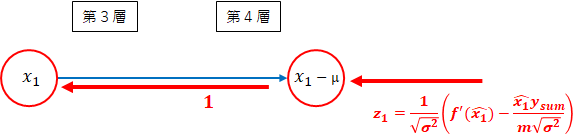
平均
各層の勾配を計算します。
-
第2層 $ \times \frac{1}{m} $
法則3($ \times $定数)より、掛けた値$ \frac{1}{m} $となります。 -
第1層 $ \sum $
法則3($ \sum $)より、$ 1 $となります。 -
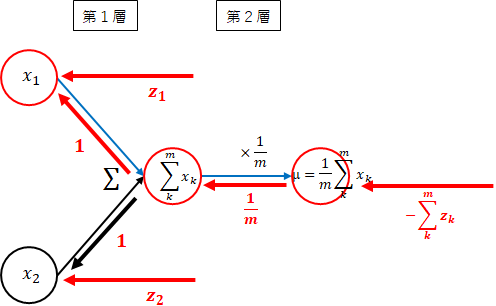
全体の勾配
平均部分の全体の勾配を求めます。全体の勾配を求めるに際し、分散で求めた勾配を利用します。
- 第2層~第1層 $ x_1 $方向
$ x_1 $では、2方向の勾配を足します。
z_1 + (-\sum_{k=1}^mz_k \times \frac{1}{m} \times 1) = z_1 - \frac{\sum_{k=1}^mz_k}{m}
一般的に、$ x_i $の勾配は、以下です。
z_i - \frac{\sum_{k=1}^mz_k}{m}
全体を1度に計算するのは大変なので、分割して計算しました。全体は、以下のようになります。
平均、分散、正規化に分けて全体の勾配を計算しましたが、層ごとに計算した方が分かりやすかったかもしれません。
実装
正規化関数
順伝播は、データの正規化のz_scoreと同じです。
平均、標準偏差(分散の平方根)を求め、正規化します。標準偏差は、0割り対策しています。
実行時には、データ系列方向に集計するためaxis=0を指定します。
# バッチ正規化
def batch_norm(x, axis = 0):
x_mean = np.mean(x, axis=axis, keepdims=True) # 平均値を求める
x_std = np.maximum(np.std(x, axis=axis, keepdims=True),1e-7) # 標準偏差を求める
xh = (x-x_mean)/x_std # 正規化
return xh
正規化の勾配関数
$ x_i $の勾配は、以下のようになりました。
\begin{align}
y_{sum} &= \sum_{k=1}^m(f^{'}(\hat{x_k}) (x_k - \mu))\\
z_i &= \frac{1}{\sqrt{\sigma^2}}(f^{'}(\hat{x_i})-\frac{\hat{x_i}y_{sum}}{m\sqrt{\sigma^2}})\\
f^{'}(x_i) &= z_i - \frac{\sum_{k=1}^mz_k}{m}
\end{align}
バッチサイズ、平均、標準偏差を利用していますので、事前に計算しておきます。
次ぐに、勾配計算を$ y_{sum} $、$ z $、$ f^{'}(x) $の順に計算します。
実行時には、データ系列方向に集計するためaxis=0を指定します。
def batch_norm_back(dy, x, axis = 0):
m = x.shape[axis] # バッチサイズ
x_mean = np.mean(x, axis=axis, keepdims=True) # 平均値を求める
x_std = np.maximum(np.std(x, axis=axis, keepdims=True),1e-7) # 標準偏差を求める
xh = (x-x_mean)/x_std # 正規化
dy_sum = np.sum(dy * (x - x_mean), axis=axis, keepdims=True)
dz = (dy - (xh * dy_sum /(m * x_std)))/ x_std
dz_sum = np.sum(dz, axis=axis, keepdims=True)
dx = dz - (dz_sum / m)
return dx
順伝播、逆伝播
正規化を適用するかどうかをregularization_paramsに設定します。
regularization_params = {"batch_norm":True}
- 順伝播
中間層に正規化関数を適用します。
勾配計算でunを利用するため、unも返却するようにしました。
# 活性化関数計算
def calc_middle(u, middle_func, middle_params, regularization_params, dropout_mask):
# バッチ正規化対応
un = u
if regularization_params.get("batch_norm"):
un = batch_norm(u, axis = 0)
# 活性化関数
z = middle_func(un, middle_params)
# ドロップアウト対応
if "dropout_middle_ratio" in regularization_params:
if dropout_mask is not None:
z = dropout(z, dropout_mask)
else:
z = z * regularization_params["dropout_middle_ratio"]
return un, z
- 逆伝播
中間層に正規化関数を適用します。unをパラメータに追加します。
# 活性化関数勾配計算
def calc_middle_back(dz, u, un, z, middle_back_func, middle_params, regularization_params, dropout_mask):
# ドロップアウト対応
if dropout_mask is not None:
dz = dropout_back(dz, dropout_mask)
# 活性化関数勾配
du = middle_back_func(dz, un, z, middle_params)
# バッチ正規化対応
if regularization_params.get("batch_norm"):
du = batch_norm_back(du, u)
return du
実行
実行して、正規化の有無で比較してみます。
他のパラメータは、既定値です。
# MNISTデータ読み込み
x_train, t_train, x_test, t_test = load_mnist('c:\\mnist\\')
regularization_params = {"batch_norm":True}
_, _, _, _, train_rate, train_err, test_rate, test_err, total_time = learn(
"batch_norm", x_train, t_train, x_test, t_test, regularization_params=regularization_params)
結果を表にします。
学習が早く進むことがわかりました。テストデータの正解率98%には、12エポックで到達しました。
| 正規化 | 学習正解 | テスト正解 | TS95% | TS97% | TS98% | TS最高 | エポック | 時間 |
|---|---|---|---|---|---|---|---|---|
| 無 | 100.00 | 97.85 | 2 | 5 | - | 97.88 | 34 | 3:49 |
| 有 | 100.00 | 98.12 | 1 | 3 | 12 | 98.17 | 43 | 4:59 |
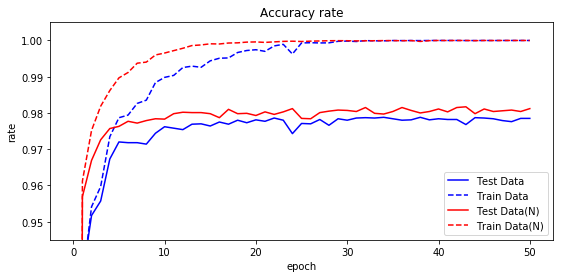
正解率をグラフ化してみます。青が正規化前、赤が正規化後です。
学習率を大きくすると良い結果が得られることもわかりました。学習率を0.5、1.0に変更して試してみます。
# MNISTデータ読み込み
x_train, t_train, x_test, t_test = load_mnist('c:\\mnist\\')
train_rates = {}
train_errs = {}
test_rates = {}
test_errs = {}
total_times = {}
regularization_params = {"batch_norm":True}
etas = [0.1,0.5,1.0]
for eta in etas:
name = "batch_norm eta=" + str(eta)
_, _, _, _, train_rates[name], train_errs[name], test_rates[name], test_errs[name], total_times[name] = learn(
name, x_train, t_train, x_test, t_test, regularization_params=regularization_params, eta=eta)
| 正規化 | 学習率 | 学習正解 | テスト正解 | TS95% | TS97% | TS98% | TS最高 | エポック |
|---|---|---|---|---|---|---|---|---|
| 無 | 0.1 | 100.00 | 97.85 | 2 | 5 | - | 97.88 | 34 |
| 有 | 0.1 | 100.00 | 98.12 | 1 | 3 | 12 | 98.17 | 43 |
| 無 | 0.5 | 100.00 | 98.23 | 1 | 3 | 20 | 98.32 | 27 |
| 有 | 0.5 | 99.99 | 98.25 | 1 | 2 | 4 | 98.35 | 43 |
| 無 | 1.0 | 98.56 | 95.92 | 4 | - | - | 96.76 | 34 |
| 有 | 1.0 | 99.99 | 98.16 | 1 | 2 | 5 | 98.37 | 47 |
そもそも学習率を0.5にするとよい結果が得られていたのですね。それは置いといたとして学習率が0.5の場合は、テストデータの正解率98%に4エポックで達しました。相当の効果です。
もう少し学習率の範囲を広げてみます。50エポック実行時のテストデータ最高正解率とその時のエポック数を正規化の有無で比較してみます。
| 学習率 | 無・TS最高 | 無・エポック | 有・TS最高 | 有・エポック |
|---|---|---|---|---|
| 0.01 | 97.17 | 48 | 97.73 | 48 |
| 0.05 | 97.78 | 32 | 98.08 | 36 |
| 0.1 | 97.88 | 34 | 98.17 | 43 |
| 0.5 | 98.32 | 27 | 98.26 | 28 |
| 1.0 | 96.76 | 34 | 98.37 | 47 |
| 5.0 | 11.35 | 10 | 98.26 | 28 |
| 10.0 | 11.35 | 5 | 98.25 | 50 |
| 50.0 | 11.35 | 18 | 98.06 | 50 |
| 100.0 | 11.35 | 7 | 97.80 | 28 |
正規化なしの場合は、学習率が5以上だと全く学習が進みません。正規化有の場合は、学習率100でもそれなりの結果となりました。
学習率を決めるのは難しいですが、正規化を行うと、少し大きめにしておけば、大丈夫であることが分かりました。
バッチ正規化
バッチ正規化では、以下のように定義し、$ \gamma $、$ \beta $を学習します。
y_i = \gamma\hat{x_i} + \beta
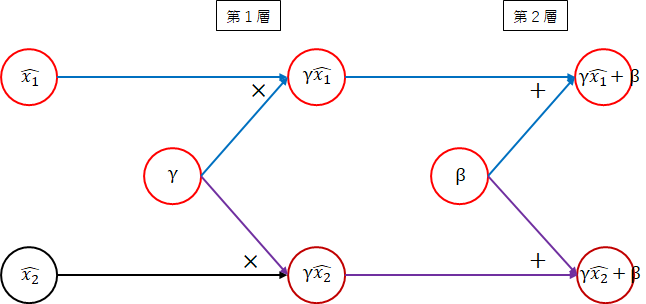
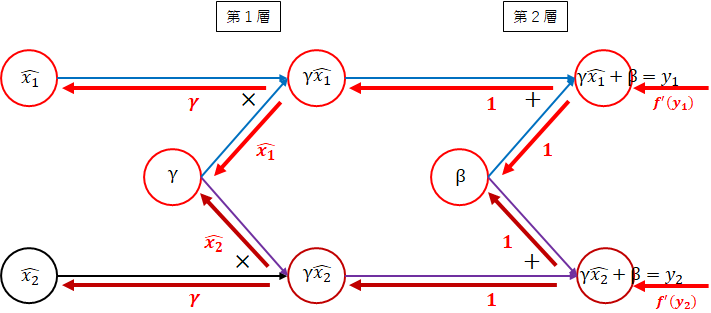
順伝播
順伝播は、以下のネットワーク図になります。
-
第1層
$ \gamma $と$ \hat{x_1} $を掛けます。 -
第2層
$ \beta $を足します。
逆伝播
逆伝播は、以下のネットワーク図になります。
-
第2層 $ + $
足し算のため$ \gamma\hat{x_1} $方向、$ \beta $方向とも1になります。 -
第1層 $ \times $
掛け算のため逆の値になります。$ \hat{x_1} $方向は、$ \gamma $、$ \gamma $方向は、$ \hat{x_1} $になります。 -
全体の勾配
全体の勾配を求めます。全体の勾配を求めるに際し、第2層への入力が必要となります。ここでは、$ f^{'}(y_1) $、$ f^{'}(y_2) $とします。 -
第2層 $ \gamma\hat{x_1} $方向
第2層への入力と$ 1 $を掛けます。
f^{'}(y_1) \times 1 = f^{'}(y_1)
一般的には、以下となります。
f^{'}(y_i)
- 第2層 $ \beta $方向
法則2により、各方向の和をとります。
(f^{'}(y_1) \times 1) + (f^{'}(y_2) \times 1) = f^{'}(y_1) + f^{'}(y_2)
一般的には、以下となります。
\sum_{k=1}^mf^{'}(y_k)
- 第1層 $ \hat{x_1} $方向
第1層への入力と$ \gamma $の掛け算になります。
f^{'}(y_1) \times \gamma = \gamma f^{'}(y_1)
一般的には、以下となります。
\gamma f^{'}(y_i)
- 第1層 $ \gamma $方向
第1層への入力と$ \hat{x_i} $の掛け算の和になります。
(f^{'}(y_1) \times \hat{x_1}) + (f^{'}(y_2) \times \hat{x_2}) = \hat{x_1}f^{'}(y_1) + \hat{x_2}f^{'}(y_2)
一般的には、以下となります。
\sum_{k=1}^m\hat{x_k}f^{'}(y_k)
実装
※当初$ \gamma $、$ \beta $をノードごとの変数としていました。層ごとに1つの変数に変更します。参考のため、ノードごとの変数の場合も残します。
バッチ正規化関数
$ \gamma $、$ \beta $をパラメータとして渡します。
$ \gamma \times \hat{x} + \beta $を計算し返却します。
def batch_norm(x, gamma, beta, axis = 0):
x_mean = np.mean(x, axis=axis, keepdims=True) # 平均値を求める
x_std = np.maximum(np.std(x, axis=axis, keepdims=True),1e-7) # 標準偏差を求める
xh = (x-x_mean)/x_std # 正規化
return gamma * xh + beta
バッチ正規化の勾配関数
$ \hat{x_i} $の勾配は、以下でした。
\gamma f^{'}(y_i)
dxに$ \gamma $を掛ける必要があります。
合わせて、$ \gamma $、$ \beta $の勾配も計算します。
$ \gamma $、$ \beta $の勾配は、以下でした。
\sum_{k=1}^m\hat{x_k}f^{'}(y_k)\\
\sum_{k=1}^mf^{'}(y_k)
$ \gamma $、$ \beta $の勾配は、各ノードごとの勾配の平均にします。
dgamma = np.sum(xh * dy)/x.shape[1]
dbeta = np.sum(dy)/x.shape[1]
参考として、$ \gamma $、$ \beta $をノードごとの変数とする場合の勾配です。
dgamma = np.sum(xh * dy, axis=axis, keepdims=True)
dbeta = np.sum(dy, axis=axis, keepdims=True)
$ \gamma $、$ \beta $の勾配を、dgamma、dbetaとして返却します。
$ \gamma $の次元が、1の場合、1つの変数、2の場合、ノードごとの変数となります。
def batch_norm_back(dy, x, gamma, beta, axis = 0):
m = x.shape[axis] # バッチサイズ
x_mean = np.mean(x, axis=axis, keepdims=True) # 平均値を求める
x_std = np.maximum(np.std(x, axis=axis, keepdims=True),1e-7) # 標準偏差を求める
xh = (x-x_mean)/x_std # 正規化
gdy = dy * gamma
dy_sum = np.sum(gdy * (x - x_mean), axis=axis, keepdims=True)
dz = (gdy - (xh * dy_sum /(m * x_std)))/ x_std
dz_sum = np.sum(dz, axis=axis, keepdims=True)
dx = dz - (dz_sum / m)
if gamma.ndim == 1:
dgamma = np.sum(xh * dy)/x.shape[1]
dbeta = np.sum(dy)/x.shape[1]
else:
dgamma = np.sum(xh * dy, axis=axis, keepdims=True)
dbeta = np.sum(dy, axis=axis, keepdims=True)
return dx, dgamma, dbeta
順伝播、逆伝播
- 順伝播
batch_norm_gamma、batch_norm_betaを個別にパラメータとして渡します。
# 活性化関数計算
def calc_middle(u, middle_func, middle_params, regularization_params, batch_norm_gamma, batch_norm_beta, dropout_mask):
# バッチ正規化対応
un = u
if regularization_params.get("batch_norm"):
un = batch_norm(u, batch_norm_gamma, batch_norm_beta)
# 活性化関数
z = middle_func(un, middle_params)
# ドロップアウト対応
if "dropout_middle_ratio" in regularization_params:
if dropout_mask is not None:
z = dropout(z, dropout_mask)
else:
z = z * regularization_params["dropout_middle_ratio"]
return un, z
- 逆伝播
batch_norm_dgamma、batch_norm_dbetaを返却するようにしました。
def calc_middle_back(dz, u, un, z, middle_back_func, middle_params, regularization_params, batch_norm_gamma, batch_norm_beta, dropout_mask):
# ドロップアウト対応
if dropout_mask is not None:
dz = dropout_back(dz, dropout_mask)
# 活性化関数勾配
du = middle_back_func(dz, un, z, middle_params)
# バッチ正規化対応
batch_norm_dgamma = None
batch_norm_dbeta = None
if regularization_params.get("batch_norm"):
du, batch_norm_dgamma, batch_norm_dbeta = batch_norm_back(du, u, batch_norm_gamma, batch_norm_beta)
return du, batch_norm_dgamma, batch_norm_dbeta
- 初期値
$ \gamma $、$ \beta $の初期値を設定します。
$ \gamma $の初期値は$ 1 $、$ \beta $の初期値は$ 0 $とします。$ \gamma $、$ \beta $の初期値で実行すると、$ \gamma $、$ \beta $を実装する前と同じ結果になります。
全体でひとつの変数とするか、ノードごとにするかを識別するために設定を行います。regularization_paramsにbatch_norm_node=Trueを設定した場合、ノードごととします。
# 正規化用、γ、β、学習率の初期化
batch_norm_params = {}
batch_norm_params["batch_norm_gamma"] = {}
batch_norm_params["batch_norm_beta"] = {}
for i in range(1, layer):
if regularization_params.get("batch_norm_node"):
batch_norm_params["batch_norm_gamma"][i] = np.ones((1, d[i]))
batch_norm_params["batch_norm_beta"][i] = np.zeros((1, d[i]))
else:
batch_norm_params["batch_norm_gamma"][i] = np.ones(1)
batch_norm_params["batch_norm_beta"][i] = np.zeros(1)
- 学習
$ \gamma $と$ \beta $の学習です。学習率は、重み、バイアスと同じくetaにしました。
ただし、$ \gamma $、$ \beta $により学習なしのパターンを実行可能なように、regularization_params["batch_norm_eta"]として設定可能にしました。regularization_params["batch_norm_eta"]=0とすると正規化の場合と同じになります。
学習率の設定
batch_norm_eta = eta
if "batch_norm_eta" in regularization_params:
batch_norm_eta = regularization_params["batch_norm_eta"]
学習
# バッチ正規化の調整
if regularization_params.get("batch_norm"):
for k in range(1, layer):
batch_norm_params["batch_norm_gamma"][k] = batch_norm_params["batch_norm_gamma"][k] - batch_norm_eta*batch_norm_dparams["batch_norm_dgamma"][k]
batch_norm_params["batch_norm_beta"][k] = batch_norm_params["batch_norm_beta"][k] - batch_norm_eta*batch_norm_dparams["batch_norm_dbeta"][k]
実行
実行してみます。
- 層ごとにひとつの$ \gamma $と$ \beta $
# MNISTデータ読み込み
x_train, t_train, x_test, t_test = load_mnist('c:\\mnist\\')
regularization_params = {"batch_norm":True}
_, _, _, _, train_rate, train_err, test_rate, test_err, total_time = learn(
"batch_norm", x_train, t_train, x_test, t_test, regularization_params=regularization_params)
- ノードごとに$ \gamma $と$ \beta $
# MNISTデータ読み込み
x_train, t_train, x_test, t_test = load_mnist('c:\\mnist\\')
regularization_params = {"batch_norm":True,"batch_norm_node":True}
_, _, _, _, train_rate, train_err, test_rate, test_err, total_time = learn(
"batch_norm", x_train, t_train, x_test, t_test, regularization_params=regularization_params)
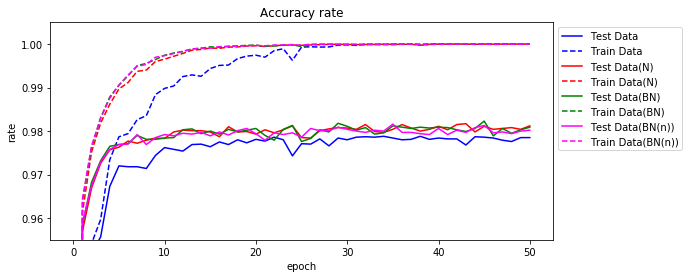
実行結果です。正規化の項目は、最初の正規化の実装をN、今回のバッチ正規化をBNとしています。参考として、ノードごとの場合をBN(n)とします。
| 正規化 | 学習正解 | テスト正解 | TS95% | TS97% | TS98% | TS最高 | エポック | 時間 |
|---|---|---|---|---|---|---|---|---|
| 無 | 100.00 | 97.85 | 2 | 5 | - | 97.88 | 34 | 3:49 |
| N | 100.00 | 98.12 | 1 | 3 | 12 | 98.17 | 43 | 4:59 |
| BN | 100.00 | 98.09 | 1 | 3 | 12 | 98.23 | 45 | 5:01 |
| BN(n) | 100.00 | 98.02 | 1 | 3 | 18 | 98.16 | 35 | 5:09 |
正解率をグラフ化してみます。緑色の線がBNの結果です。
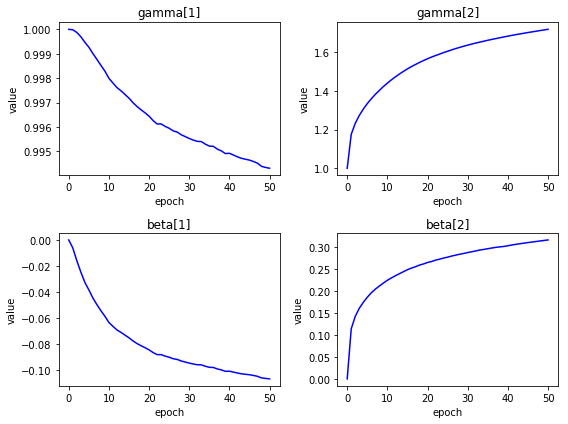
- 層ごとにひとつの$ \gamma $と$ \beta $
エポックごとに、$ \gamma $と$ \beta $がどのように変化したか確認してみます。
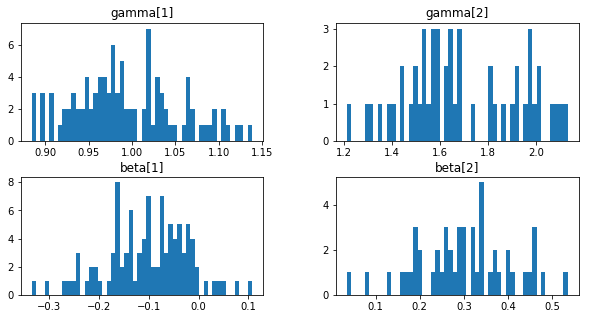
- ノードごとに$ \gamma $と$ \beta $
学習後の$ \gamma $、$ \beta $の分布をヒストグラムにします。
学習率0.5,1.0の場合の正解率を比較のため表にしました。
| 正規化 | 学習率 | 学習正解 | テスト正解 | TS95% | TS97% | TS98% | TS最高 | エポック |
|---|---|---|---|---|---|---|---|---|
| 無 | 0.1 | 100.00 | 97.85 | 2 | 5 | - | 97.88 | 34 |
| N | 0.1 | 100.00 | 98.12 | 1 | 3 | 12 | 98.17 | 43 |
| BN | 0.1 | 100.00 | 98.09 | 1 | 3 | 12 | 98.23 | 45 |
| BN(n) | 0.1 | 100.00 | 98.02 | 1 | 3 | 18 | 98.16 | 35 |
| 無 | 0.5 | 100.00 | 98.23 | 1 | 3 | 20 | 98.32 | 27 |
| N | 0.5 | 99.99 | 98.25 | 1 | 2 | 4 | 98.35 | 43 |
| BN | 0.5 | 100.00 | 98.24 | 1 | 2 | 4 | 98.26 | 19 |
| BN(n) | 0.5 | 99.97 | 98.15 | 1 | 2 | 10 | 98.15 | 27 |
| 無 | 1.0 | 98.56 | 95.92 | 4 | - | - | 96.76 | 34 |
| N | 1.0 | 99.99 | 98.16 | 1 | 2 | 5 | 98.37 | 47 |
| BN | 1.0 | 99.99 | 98.11 | 1 | 1 | 7 | 98.24 | 35 |
| BN(n) | 1.0 | 99.99 | 98.16 | 1 | 1 | 7 | 98.24 | 45 |
学習率が0.1の場合は良くなりましたが、その他は悪くなりました。
もう少し学習率の範囲を広げてみます。50エポック実行時のテストデータ最高正解率とその時のエポック数をバッチ正規化の有無で比較してみます。学習率を大きくしすぎると学習が進みませんでした。
| 学習率 | 無・TS最高 | 無・エポック | N・TS最高 | N・エポック | BN・TS最高 | BN・エポック | BN(n)・TS最高 | BN(n)・エポック |
|---|---|---|---|---|---|---|---|---|
| 0.01 | 97.17 | 48 | 97.73 | 48 | 97.75 | 40 | 97.74 | 37 |
| 0.05 | 97.78 | 32 | 98.08 | 36 | 98.12 | 40 | 98.00 | 29 |
| 0.1 | 97.88 | 34 | 98.17 | 43 | 98.23 | 45 | 98.16 | 35 |
| 0.5 | 98.32 | 27 | 98.35 | 43 | 98.26 | 19 | 98.15 | 27 |
| 1.0 | 96.76 | 34 | 98.37 | 47 | 98.24 | 35 | 98.24 | 45 |
| 5.0 | 11.35 | 10 | 98.26 | 28 | 98.30 | 40 | 98.19 | 50 |
| 10.0 | 11.35 | 5 | 98.25 | 50 | 11.35 | 5 | 11.35 | 5 |
| 50.0 | 11.35 | 18 | 98.06 | 50 | 11.35 | 19 | 11.35 | 2 |
| 100.0 | 11.35 | 7 | 97.80 | 28 | 11.35 | 7 | 11.35 | 10 |
参考のため、$ \gamma $、$ \beta $の学習率を別に設定して試してみました。
- 層ごとにひとつの$ \gamma $と$ \beta $
# MNISTデータ読み込み
x_train, t_train, x_test, t_test = load_mnist('c:\\mnist\\')
train_rates = {}
train_errs = {}
test_rates = {}
test_errs = {}
total_times = {}
batch_norm_etas = [0.01,0.05,0.1,0.5,1.0,5.0,10.0,50.0,100.0]
for batch_norm_eta in batch_norm_etas:
regularization_params = {"batch_norm":True,"batch_norm_eta":batch_norm_eta}
name = "BN batch_norm_eta=" + str(batch_norm_eta)
_, _, _, _, train_rates[name], train_errs[name], test_rates[name], test_errs[name], total_times[name] = learn(
name, x_train, t_train, x_test, t_test, regularization_params=regularization_params)
| BN学習率 | 学習正解 | テスト正解 | TS95% | TS97% | TS98% | TS最高 | エポック |
|---|---|---|---|---|---|---|---|
| 0.01 | 100.00 | 98.05 | 1 | 3 | 12 | 98.17 | 29 |
| 0.05 | 100.00 | 98.10 | 1 | 3 | 12 | 98.21 | 36 |
| 0.1 | 100.00 | 98.09 | 1 | 3 | 12 | 98.23 | 45 |
| 0.5 | 100.00 | 97.86 | 1 | 3 | 12 | 98.17 | 42 |
| 1.0 | 100.00 | 98.04 | 1 | 3 | 32 | 98.11 | 37 |
| 5.0 | 100.00 | 98.06 | 1 | 3 | 14 | 98.21 | 42 |
| 10.0 | 99.99 | 97.69 | 1 | 3 | 36 | 98.03 | 36 |
| 50.0 | 99.99 | 97.85 | 2 | 4 | - | 97.96 | 48 |
| 100.0 | 99.96 | 97.77 | 1 | 4 | 40 | 98.00 | 40 |
- ノードごとに$ \gamma $と$ \beta $
| BN(n)学習率 | 学習正解 | テスト正解 | TS95% | TS97% | TS98% | TS最高 | エポック |
|---|---|---|---|---|---|---|---|
| 0.01 | 100.00 | 98.01 | 1 | 3 | 12 | 98.13 | 42 |
| 0.05 | 100.00 | 98.13 | 1 | 3 | 12 | 98.17 | 36 |
| 0.1 | 100.00 | 98.02 | 1 | 3 | 18 | 98.16 | 35 |
| 0.5 | 100.00 | 97.99 | 1 | 3 | 29 | 98.02 | 29 |
| 1.0 | 99.99 | 97.95 | 1 | 2 | 26 | 98.14 | 29 |
| 5.0 | 99.99 | 97.72 | 1 | 3 | - | 97.85 | 38 |
| 10.0 | 98.99 | 97.88 | 1 | 4 | - | 97.91 | 42 |
| 50.0 | 99.86 | 97.26 | 2 | 4 | - | 97.71 | 32 |
| 100.0 | 99.61 | 97.32 | 2 | 9 | - | 97.56 | 20 |
判明したこと
正解率が向上することがわかりました。特に、学習率への依存度が少なくなり、学習率の選定に幅を持つことができます。
$ \gamma $、$ \beta $を導入してもあまり改善しませんでした。実装が間違っているのか、MNISTのためなのかわかりません。
参考
関数群です。
import gzip
import numpy as np
# MNIST読み込み
def load_mnist( mnist_path ) :
return _load_image(mnist_path + 'train-images-idx3-ubyte.gz'), \
_load_label(mnist_path + 'train-labels-idx1-ubyte.gz'), \
_load_image(mnist_path + 't10k-images-idx3-ubyte.gz'), \
_load_label(mnist_path + 't10k-labels-idx1-ubyte.gz')
def _load_image( image_path ) :
# 画像データの読み込み
with gzip.open(image_path, 'rb') as f:
buffer = f.read()
size = np.frombuffer(buffer, np.dtype('>i4'), 1, offset=4)
rows = np.frombuffer(buffer, np.dtype('>i4'), 1, offset=8)
columns = np.frombuffer(buffer, np.dtype('>i4'), 1, offset=12)
data = np.frombuffer(buffer, np.uint8, offset=16)
image = np.reshape(data, (size[0], rows[0]*columns[0]))
image = image.astype(np.float32)
return image
def _load_label( label_path ) :
# 正解データ読み込み
with gzip.open(label_path, 'rb') as f:
buffer = f.read()
size = np.frombuffer(buffer, np.dtype('>i4'), 1, offset=4)
data = np.frombuffer(buffer, np.uint8, offset=8)
label = np.zeros((size[0], 10))
for i in range(size[0]):
label[i, data[i]] = 1
return label
# 正規化関数
def min_max(x, stats, params):
axis=params.get("axis")
if "min" not in stats:
stats["min"] = np.min(x, axis=axis, keepdims=True) # 最小値を求める
if "max" not in stats:
stats["max"] = np.max(x, axis=axis, keepdims=True) # 最大値を求める
return (x-stats["min"])/np.maximum((stats["max"]-stats["min"]),1e-7), stats
def z_score(x, stats, params):
axis=params.get("axis")
if "mean" not in stats:
stats["mean"] = np.mean(x, axis=axis, keepdims=True) # 平均値を求める
if "std" not in stats:
stats["std"] = np.std(x, axis=axis, keepdims=True) # 標準偏差を求める
return (x-stats["mean"])/np.maximum(stats["std"],1e-7), stats
# affine変換
def affine(z, W, b):
return np.dot(z, W) + b
def affine_back(du, z, W, b):
dz = np.dot(du, W.T) # zの勾配は、今までの勾配と重みを掛けた値
dW = np.dot(z.T, du) # 重みの勾配は、zに今までの勾配を掛けた値
size = 1
if z.ndim == 2:
size = z.shape[0]
db = np.dot(np.ones(size).T, du) # バイアスの勾配は、今までの勾配の値
return dz, dW, db
# 活性化関数(中間)
def sigmoid(u, params):
return 1/(1 + np.exp(-u))
def sigmoid_back(dz, u, z, params):
return dz * (z - z**2)
def tanh(u, params):
return np.tanh(u)
def tanh_back(dz, u, z, params):
return dz * (1/np.cosh(u)**2)
def relu(u, params):
return np.maximum(0, u)
def relu_back(dz, u, z, params):
return dz * np.where(u > 0, 1, 0)
def leaky_relu(u, params):
return np.maximum(u * params["alpha"], u)
def leaky_relu_back(dz, u, z, params):
return dz * np.where(u > 0, 1, params["alpha"])
def identity(u, params):
return u
def identity_back(dz, u, z, params):
return dz
def softplus(u, params):
return np.log(1+np.exp(u))
def softplus_back(dz, u, z, params):
return dz * (1/(1 + np.exp(-u)))
def softsign(u, params):
return u/(1+np.absolute(u))
def softsign_back(dz, u, z, params):
return dz * (1/(1+np.absolute(u))**2)
def step(u, params):
return np.where(u > 0, 1, 0)
def step_back(dz, u, x, params):
return 0
# 活性化関数(出力)
def softmax(u, params):
u = u.T
max_u = np.max(u, axis=0)
exp_u = np.exp(u - max_u)
sum_exp_u = np.sum(exp_u, axis=0)
y = exp_u/sum_exp_u
return y.T
# 損失関数
def mean_squared_error(y, t):
size = 1
if y.ndim == 2:
size = y.shape[0]
return 0.5 * np.sum((y-t)**2)/size
def cross_entropy_error(y, t):
size = 1
if y.ndim == 2:
size = y.shape[0]
return -np.sum(t * np.log(np.maximum(y,1e-7)))/size
#return -np.sum(t * np.log(y))/size
# 活性化関数(出力)+損失関数勾配
def softmax_cross_entropy_error_back(y, u, t):
size = 1
if y.ndim == 2:
size = y.shape[0]
return (y - t)/size
def identity_mean_squared_error_back(y, u, t):
size = 1
if y.ndim == 2:
size = y.shape[0]
return (y - t)/size
# 重み・バイアスの初期化
def lecun_normal(d_1, d, params):
var = 1/np.sqrt(d_1)
return np.random.normal(0, var, (d_1, d))
def lecun_uniform(d_1, d, params):
min = -np.sqrt(3/d_1)
max = np.sqrt(3/d_1)
return np.random.uniform(min, max, (d_1, d))
def glorot_normal(d_1, d, params):
var = np.sqrt(2/(d_1+d))
return np.random.normal(0, var, (d_1, d))
def glorot_uniform(d_1, d, params):
min = -np.sqrt(6/(d_1+d))
max = np.sqrt(6/(d_1+d))
return np.random.uniform(min, max, (d_1, d))
def he_normal(d_1, d, params):
var = np.sqrt(2/d_1)
return np.random.normal(0, var, (d_1, d))
def he_uniform(d_1, d, params):
min = -np.sqrt(6/d_1)
max = np.sqrt(6/d_1)
return np.random.uniform(min, max, (d_1, d))
def normal_w(d_1, d, params):
mean=0
var=1
if "mean" in params:
mean = params["mean"]
if "var" in params:
var = params["var"]
return np.random.normal(mean, var, (d_1, d))
def normal_b(d, params):
mean=0
var=1
if "mean" in params:
mean = params["mean"]
if "var" in params:
var = params["var"]
return np.random.normal(mean, var, d)
def uniform_w(d_1, d, params):
min=0
max=1
if "min" in params:
min = params["min"]
if "max" in params:
max = params["max"]
return np.random.uniform(min, max, (d_1, d))
def uniform_b(d, params):
min=0
max=1
if "min" in params:
min = params["min"]
if "max" in params:
max = params["max"]
return np.random.uniform(min, max, d)
def zeros_w(d_1, d, params):
return np.zeros((d_1, d))
def zeros_b(d, params):
return np.zeros(d)
def ones_w(d_1, d, params):
return np.ones((d_1, d))
def ones_b(d, params):
return np.ones(d)
# 重み減衰
def L1_norm(W, weight_decay_lambda):
r = 0.
for WI in W.values():
r = r + np.sum(np.absolute(WI))
return weight_decay_lambda * r
def L1_norm_back(W, weight_decay_lambda):
return np.where(W > 0, weight_decay_lambda, np.where(W < 0, -weight_decay_lambda, 0))
def L2_norm(W, weight_decay_lambda):
r = 0.
for WI in W.values():
r = r + np.sum(WI**2)
return (weight_decay_lambda * r)/2
def L2_norm_back(W, weight_decay_lambda):
return weight_decay_lambda * W
# ドロップアウト
def dropout(z, mask):
return z * mask
def dropout_back(dz, mask):
return dz * mask
# バッチ正規化
def batch_norm(x, gamma, beta, axis = 0):
x_mean = np.mean(x, axis=axis, keepdims=True) # 平均値を求める
x_std = np.maximum(np.std(x, axis=axis, keepdims=True),1e-7) # 標準偏差を求める
xh = (x-x_mean)/x_std # 正規化
return gamma * xh + beta
def batch_norm_back(dy, x, gamma, beta, axis = 0):
m = x.shape[axis] # バッチサイズ
x_mean = np.mean(x, axis=axis, keepdims=True) # 平均値を求める
x_std = np.maximum(np.std(x, axis=axis, keepdims=True),1e-7) # 標準偏差を求める
xh = (x-x_mean)/x_std # 正規化
gdy = dy * gamma
dy_sum = np.sum(gdy * (x - x_mean), axis=axis, keepdims=True)
dz = (gdy - (xh * dy_sum /(m * x_std)))/ x_std
dz_sum = np.sum(dz, axis=axis, keepdims=True)
dx = dz - (dz_sum / m)
if gamma.ndim == 1:
dgamma = np.sum(xh * dy)/x.shape[1]
dbeta = np.sum(dy)/x.shape[1]
else:
dgamma = np.sum(xh * dy, axis=axis, keepdims=True)
dbeta = np.sum(dy, axis=axis, keepdims=True)
return dx, dgamma, dbeta
# 正解率
def accuracy_rate(y, t):
max_y = np.argmax(y, axis=1)
max_t = np.argmax(t, axis=1)
return np.sum(max_y == max_t)/y.shape[0]
順伝播、逆伝播は複雑になってきたため、関数との対応を図に示します。
import numpy as np
# ドロップアウト
def set_dropout_mask(d, regularization_params):
mask = {}
if "dropout_input_ratio" in regularization_params:
mask[0] = np.zeros(d[0])
ratio = regularization_params["dropout_input_ratio"]
mask_idx = np.random.choice(d[0], round(ratio*d[0]), replace=False) # 通すindexの配列
mask[0][mask_idx] = 1
if "dropout_middle_ratio" in regularization_params:
for i in range(1, len(d)-1):
mask[i] = np.zeros(d[i])
ratio = regularization_params["dropout_middle_ratio"]
mask_idx = np.random.choice(d[i], round(ratio*d[i]), replace=False) # 通すindexの配列
mask[i][mask_idx] = 1
return mask
# affin計算
def calc_affine(z, W, b):
return affine(z, W, b)
# affin勾配計算
def calc_affine_back(du, z, W, b, regularization_params):
dz, dW, db = affine_back(du, z, W, b)
if "weight_decay_func" in regularization_params: # 重み減衰対応
dW = dW + regularization_params["weight_decay_back_func"](W, regularization_params["weight_decay_lambda"])
return dz, dW, db
# 入力計算
def calc_input(x, regularization_params, dropout_mask):
# ドロップアウト対応
if "dropout_input_ratio" in regularization_params:
if dropout_mask is not None:
x = dropout(x, dropout_mask)
else:
x = x * regularization_params["dropout_input_ratio"]
return x
# 活性化関数計算
def calc_middle(u, middle_func, middle_params, regularization_params, batch_norm_gamma, batch_norm_beta, dropout_mask):
# バッチ正規化対応
un = u
if regularization_params.get("batch_norm"):
un = batch_norm(u, batch_norm_gamma, batch_norm_beta)
# 活性化関数
z = middle_func(un, middle_params)
# ドロップアウト対応
if "dropout_middle_ratio" in regularization_params:
if dropout_mask is not None:
z = dropout(z, dropout_mask)
else:
z = z * regularization_params["dropout_middle_ratio"]
return un, z
# 活性化関数勾配計算
def calc_middle_back(dz, u, un, z, middle_back_func, middle_params, regularization_params, batch_norm_gamma, batch_norm_beta, dropout_mask):
# ドロップアウト対応
if dropout_mask is not None:
dz = dropout_back(dz, dropout_mask)
# 活性化関数勾配
du = middle_back_func(dz, un, z, middle_params)
# バッチ正規化対応
batch_norm_dgamma = None
batch_norm_dbeta = None
if regularization_params.get("batch_norm"):
du, batch_norm_dgamma, batch_norm_dbeta = batch_norm_back(du, u, batch_norm_gamma, batch_norm_beta)
return du, batch_norm_dgamma, batch_norm_dbeta
# 誤差計算
def calc_error(y, t, W, error_func, regularization_params):
e = error_func(y, t)
if "weight_decay_func" in regularization_params: # 重み減衰対応
e = e + regularization_params["weight_decay_func"](W, regularization_params["weight_decay_lambda"])
return e
# 順伝播
def propagation(layer, x, W, b, middle_func, middle_params, output_func, output_params, regularization_params, batch_norm_params, dropout_mask={}):
u = {}
un = {}
z = {}
# 入力層
#z[0] = x
z[0] = calc_input(x, regularization_params, dropout_mask.get(0))
# 中間層
for i in range(1, layer):
u[i] = calc_affine(z[i-1], W[i], b[i])
#z[i] = middle_func(u[i], middle_params)
un[i], z[i] = calc_middle(u[i], middle_func, middle_params, regularization_params, batch_norm_params["batch_norm_gamma"][i], batch_norm_params["batch_norm_beta"][i], dropout_mask.get(i))
# 出力層
u[layer] = calc_affine(z[layer-1], W[layer], b[layer])
y = output_func(u[layer], output_params)
return u, un, z, y
# 逆伝播
def back_propagation(layer, u, un, z, y, t, W, b, middle_back_func, middle_params, output_error_back_func, regularization_params, batch_norm_params, dropout_mask={}):
du = {}
dz = {}
dW = {}
db = {}
batch_norm_dparams = {}
batch_norm_dparams["batch_norm_dgamma"] = {}
batch_norm_dparams["batch_norm_dbeta"] = {}
# 出力層
du[layer] = output_error_back_func(y, u[layer], t)
dz[layer-1], dW[layer], db[layer] = calc_affine_back(du[layer], z[layer-1], W[layer], b[layer], regularization_params)
# 中間層
for i in range(layer-1, 0, -1):
#du[i] = middle_back_func(dz[i], u[i], z[i], middle_params)
du[i], batch_norm_dparams["batch_norm_dgamma"][i], batch_norm_dparams["batch_norm_dbeta"][i] = calc_middle_back(dz[i], u[i], un[i], z[i], middle_back_func, middle_params, regularization_params, batch_norm_params["batch_norm_gamma"][i], batch_norm_params["batch_norm_beta"][i], dropout_mask.get(i))
dz[i-1], dW[i], db[i] = calc_affine_back(du[i], z[i-1], W[i], b[i], regularization_params)
return du, dz, dW, db, batch_norm_dparams
パラメータです。
| パラメータ | 既定値 | パラメータ値 |
|---|---|---|
| 中間層ノード数 | [100,50] | - |
| 重み初期化関数 | he_normal | lecun_normal,lecun_uniform, glorot_normal,glorot_uniform, he_normal,he_uniform, normal_w,uniform_w, zeros_w,ones_w |
| 重み初期化関数パラメータ | - | normal_wの場合、"mean"、"var" uniform_wの場合、"min"、"max" |
| バイアス初期化関数 | zeros_b | normal_b,uniform_b, zeros_b,ones_b |
| バイアス初期化関数パラメータ | - | normal_bの場合、"mean"、"var" uniform_bの場合、"min"、"max" |
| 学習率 | 0.1 | - |
| バッチサイズ | 100 | - |
| エポック数 | 50 | - |
| データ正規化関数 | min_max | min_max,z_score |
| データ正規化関数パラメータ | - | "axis":0、"axis":None |
| 中間層活性化関数 | relu | sigmoid,tanh,relu,leaky_relu, identity,softplus,softsign,step |
| 中間層活性化関数パラメータ | - | leaky_reluの場合、"alpha" |
| 出力層活性化関数 | softmax | softmax,identity |
| 出力層活性化関数パラメータ | - | - |
| 損失関数 | cross_entropy_error | mean_squared_error,cross_entropy_error |
| 正則化パラメータ | - | "weight_decay_func":L1_norm,L2_norm "weight_decay_lambda":重み定数 "dropout_input_ratio":入力層に対するドロップアウト率 "dropout_middle_ratio":中間層に対するドロップアウト率 "batch_norm":バッチ正規化有無(True,False) "batch_norm_eta":バッチ正規化学習率 |
| 学習データシャフルフラグ | True | True,False |
import numpy as np
import time
# 学習
def learn(
name, # 学習識別名
x_train, # 学習データ
t_train, # 学習正解
x_test, # テストデータ
t_test, # テスト正解
md=[100, 50], # 中間層ノード数
weight_init_func=he_normal, # 重み初期化関数
weight_init_params={}, # 重み初期化関数パラメータ
bias_init_func=zeros_b, # バイアス初期化関数
bias_init_params={}, # バイアス初期化関数パラメータ
eta=0.1, # 学習率
batch_size=100, # バッチサイズ
epoch=50, # エポック数
data_norm_func=min_max, # データ正規化関数
data_norm_params={}, # データ正規化関数パラメータ
middle_func=relu, # 中間層活性化関数
middle_params={}, # 中間層活性化関数パラメータ
output_func=softmax, # 出力層活性化関数
output_params={}, # 出力層活性化関数パラメータ
error_func=cross_entropy_error, # 損失関数
regularization_params={}, # 正則化パラメータ
shuffle_flag=True # 学習データシャフルフラグ
):
# 学習識別名表示
print(name)
# ノード数
d = [x_train.shape[x_train.ndim-1]] + md + [t_train.shape[t_train.ndim-1]]
# 階層数
layer = len(d) - 1
# 重み、バイアスの初期化
W = {}
b = {}
for i in range(layer):
W[i+1] = weight_init_func(d[i], d[i+1], weight_init_params)
for i in range(layer):
b[i+1] = bias_init_func(d[i+1], bias_init_params)
# 入力データの正規化
stats = {}
nx_train, train_stats = data_norm_func(x_train, stats, data_norm_params)
nx_test, test_stats = data_norm_func(x_test, train_stats, data_norm_params)
# 正解率、誤差初期化
train_rate = np.zeros(epoch+1)
test_rate = np.zeros(epoch+1)
train_err = np.zeros(epoch+1)
test_err = np.zeros(epoch+1)
# 勾配関数
middle_back_func = eval(middle_func.__name__ + "_back")
output_error_back_func = eval(output_func.__name__ + "_" + error_func.__name__ + "_back")
if "weight_decay_func" in regularization_params: # 重み減衰
regularization_params["weight_decay_back_func"] = eval(regularization_params["weight_decay_func"].__name__ + "_back")
# 正規化用、γ、β、学習率の初期化
batch_norm_params = {}
batch_norm_params["batch_norm_gamma"] = {}
batch_norm_params["batch_norm_beta"] = {}
for i in range(1, layer):
if regularization_params.get("batch_norm_node"):
batch_norm_params["batch_norm_gamma"][i] = np.ones((1, d[i]))
batch_norm_params["batch_norm_beta"][i] = np.zeros((1, d[i]))
else:
batch_norm_params["batch_norm_gamma"][i] = np.ones(1)
batch_norm_params["batch_norm_beta"][i] = np.zeros(1)
batch_norm_eta = eta
if "batch_norm_eta" in regularization_params:
batch_norm_eta = regularization_params["batch_norm_eta"]
# 実行(学習データ)
u_train, un_train, z_train, y_train = propagation(layer, nx_train, W, b, middle_func, middle_params, output_func, output_params, regularization_params, batch_norm_params)
train_rate[0] = accuracy_rate(y_train, t_train)
#train_err[0] = error_func(y_train, t_train)
train_err[0] = calc_error(y_train, t_train, W, error_func, regularization_params)
# 実行(テストデータ)
u_test, un_test, z_test, y_test = propagation(layer, nx_test, W, b, middle_func, middle_params, output_func, output_params, regularization_params, batch_norm_params)
test_rate[0] = accuracy_rate(y_test, t_test)
#test_err[0] = error_func(y_test, t_test)
test_err[0] = calc_error(y_test, t_test, W, error_func, regularization_params)
# 正解率、誤差表示
print(" 学習データ正解率 = " + str(train_rate[0]) + " テストデータ正解率 = " + str(test_rate[0]) +
" 学習データ誤差 = " + str(train_err[0]) + " テストデータ誤差 = " + str(test_err[0]))
# 開始時刻設定
start_time = time.time()
for i in range(epoch):
# 学習データシャッフル
nx = nx_train
t = t_train
if shuffle_flag:
# データのシャッフル(正解データも同期してシャフルする必要があるため一度、結合し分離)
nx_t = np.concatenate([nx_train, t_train], axis=1)
np.random.shuffle(nx_t)
nx, t = np.split(nx_t, [nx_train.shape[1]], axis=1)
# 学習
for j in range(0, nx.shape[0], batch_size):
# ドロップアウトマスクの設定
dropout_mask = set_dropout_mask(d, regularization_params)
# 実行
u, un, z, y = propagation(layer, nx[j:j+batch_size], W, b, middle_func, middle_params, output_func, output_params,
regularization_params, batch_norm_params, dropout_mask)
# 勾配を計算
du, dz, dW, db, batch_norm_dparams = back_propagation(layer, u, un, z, y, t[j:j+batch_size], W, b, middle_back_func, middle_params, output_error_back_func,
regularization_params, batch_norm_params, dropout_mask)
# 重み、バイアスの調整
for k in range(1, layer+1):
W[k] = W[k] - eta*dW[k]
b[k] = b[k] - eta*db[k]
# バッチ正規化の調整
if regularization_params.get("batch_norm"):
for k in range(1, layer):
batch_norm_params["batch_norm_gamma"][k] = batch_norm_params["batch_norm_gamma"][k] - batch_norm_eta*batch_norm_dparams["batch_norm_dgamma"][k]
batch_norm_params["batch_norm_beta"][k] = batch_norm_params["batch_norm_beta"][k] - batch_norm_eta*batch_norm_dparams["batch_norm_dbeta"][k]
# 重み、バイアス調整後の実行(学習データ)
u_train, un_train, z_train, y_train = propagation(layer, nx_train, W, b, middle_func, middle_params, output_func, output_params, regularization_params, batch_norm_params)
train_rate[i+1] = accuracy_rate(y_train, t_train)
#train_err[i+1] = error_func(y_train, t_train)
train_err[i+1] = calc_error(y_train, t_train, W, error_func, regularization_params)
# 重み、バイアス調整後の実行(テストデータ)
u_test, un_test, z_test, y_test = propagation(layer, nx_test, W, b, middle_func, middle_params, output_func, output_params, regularization_params, batch_norm_params)
test_rate[i+1] = accuracy_rate(y_test, t_test)
#test_err[i+1] = error_func(y_test, t_test)
test_err[i+1] = calc_error(y_test, t_test, W, error_func, regularization_params)
# 正解率、誤差表示
print(str(i+1) + " 学習データ正解率 = " + str(train_rate[i+1]) + " テストデータ正解率 = " + str(test_rate[i+1]) +
" 学習データ誤差 = " + str(train_err[i+1]) + " テストデータ誤差 = " + str(test_err[i+1]))
# 終了時刻設定
end_time = time.time()
total_time = end_time - start_time
print("所要時間 = " +str(int(total_time/60))+" 分 "+str(int(total_time%60)) + " 秒")
return y_train, y_test, W, b, train_rate, train_err, test_rate, test_err, total_time
改版履歴
2018/6/23 バッチ正則化実装見直し