前回は、パラメータを1つ1つ変更して試してみました。結局、どのパラメータの組み合わせがよいのかよくわかりませんでした。パラメータをランダムに変更して試してみます。データは、MNISTを利用します。
実装変更
パラメータを渡し繰り返し実行できるようにプログラムを変更します。
関数
活性化関数など関数をパラメータで指定可能とします。そのため、関数種別ごとに関数の引数を統一します。
# 正規化関数
def data_norm_func(x, stats, params):
return nx, stats
# 活性化関数(中間)
def middle_func(u, params):
return z
def middle_back_func(dz, u, z, params):
return du
# 活性化関数(出力)
def output_func(u, params):
return y
# 損失関数
def error_func(y, t):
return e
# 活性化関数(出力)+損失関数勾配
def output_error_back_func(y, u, t):
return du
# 重み・バイアスの初期化
def weight_init_func(d_1, d, params):
return W
def bias_init_func(d, params):
return b
活性化関数の勾配関数は、活性化関数名+"_back"としています。活性関数がreluの場合、勾配関数は、relu_backです。出力層の活性化関数と損失関数まとめて勾配関数を作成しています。出力層の活性化関数名+勾配関数名+"_back"とします。
関数名の結合にevalを利用しています。
# 勾配関数
middle_back_func = eval(middle_func.__name__ + "_back")
output_error_back_func = eval(output_func.__name__ + "_" + error_func.__name__ + "_back")
以下のように変更しました。
# 正規化関数
def min_max(x, stats, params):
axis=params.get("axis")
if "min" not in stats:
stats["min"] = np.min(x, axis=axis, keepdims=True) # 最小値を求める
if "max" not in stats:
stats["max"] = np.max(x, axis=axis, keepdims=True) # 最大値を求める
return (x-stats["min"])/np.maximum((stats["max"]-stats["min"]),1e-7), stats
def z_score(x, stats, params):
axis=params.get("axis")
if "mean" not in stats:
stats["mean"] = np.mean(x, axis=axis, keepdims=True) # 平均値を求める
if "std" not in stats:
stats["std"] = np.std(x, axis=axis, keepdims=True) # 標準偏差を求める
return (x-stats["mean"])/np.maximum(stats["std"],1e-7), stats
# affine変換
def affine(z, W, b):
return np.dot(z, W) + b
def affine_back(du, z, W, b):
dz = np.dot(du, W.T) # zの勾配は、今までの勾配と重みを掛けた値
dW = np.dot(z.T, du) # 重みの勾配は、zに今までの勾配を掛けた値
size = 1
if z.ndim == 2:
size = z.shape[0]
db = np.dot(np.ones(size).T, du) # バイアスの勾配は、今までの勾配の値
return dz, dW, db
# 活性化関数(中間)
def sigmoid(u, params):
return 1/(1 + np.exp(-u))
def sigmoid_back(dz, u, z, params):
return dz * (z - z**2)
def tanh(u, params):
return np.tanh(u)
def tanh_back(dz, u, z, params):
return dz * (1/np.cosh(u)**2)
def relu(u, params):
return np.maximum(0, u)
def relu_back(dz, u, z, params):
return dz * np.where(u > 0, 1, 0)
def leaky_relu(u, params):
return np.maximum(u * params["alpha"], u)
def leaky_relu_back(dz, u, z, params):
return dz * np.where(u > 0, 1, params["alpha"])
def identity(u, params):
return u
def identity_back(dz, u, z, params):
return dz
def softplus(u, params):
return np.log(1+np.exp(u))
def softplus_back(dz, u, z, params):
return dz * (1/(1 + np.exp(-u)))
def softsign(u, params):
return u/(1+np.absolute(u))
def softsign_back(dz, u, z, params):
return dz * (1/(1+np.absolute(u))**2)
def step(u, params):
return np.where(u > 0, 1, 0)
def step_back(dz, u, x, params):
return 0
# 活性化関数(出力)
def softmax(u, params):
u = u.T
max_u = np.max(u, axis=0)
exp_u = np.exp(u - max_u)
sum_exp_u = np.sum(exp_u, axis=0)
y = exp_u/sum_exp_u
return y.T
# 損失関数
def mean_squared_error(y, t):
size = 1
if y.ndim == 2:
size = y.shape[0]
return 0.5 * np.sum((y-t)**2)/size
def cross_entropy_error(y, t):
size = 1
if y.ndim == 2:
size = y.shape[0]
return -np.sum(t * np.log(np.maximum(y,1e-7)))/size
#return -np.sum(t * np.log(y))/size
# 活性化関数(出力)+損失関数勾配
def softmax_cross_entropy_error_back(y, u, t):
size = 1
if y.ndim == 2:
size = y.shape[0]
return (y - t)/size
def identity_mean_squared_error_back(y, u, t):
size = 1
if y.ndim == 2:
size = y.shape[0]
return (y - t)/size
# 重み・バイアスの初期化
def lecun_normal(d_1, d, params):
var = 1/np.sqrt(d_1)
return np.random.normal(0, var, (d_1, d))
def lecun_uniform(d_1, d, params):
min = -np.sqrt(3/d_1)
max = np.sqrt(3/d_1)
return np.random.uniform(min, max, (d_1, d))
def glorot_normal(d_1, d, params):
var = np.sqrt(2/(d_1+d))
return np.random.normal(0, var, (d_1, d))
def glorot_uniform(d_1, d, params):
min = -np.sqrt(6/(d_1+d))
max = np.sqrt(6/(d_1+d))
return np.random.uniform(min, max, (d_1, d))
def he_normal(d_1, d, params):
var = np.sqrt(2/d_1)
return np.random.normal(0, var, (d_1, d))
def he_uniform(d_1, d, params):
min = -np.sqrt(6/d_1)
max = np.sqrt(6/d_1)
return np.random.uniform(min, max, (d_1, d))
def normal_w(d_1, d, params):
mean=0
var=1
if "mean" in params:
mean = params["mean"]
if "var" in params:
var = params["var"]
return np.random.normal(mean, var, (d_1, d))
def normal_b(d, params):
mean=0
var=1
if "mean" in params:
mean = params["mean"]
if "var" in params:
var = params["var"]
return np.random.normal(mean, var, d)
def uniform_w(d_1, d, params):
min=0
max=1
if "min" in params:
min = params["min"]
if "max" in params:
max = params["max"]
return np.random.uniform(min, max, (d_1, d))
def uniform_b(d, params):
min=0
max=1
if "min" in params:
min = params["min"]
if "max" in params:
max = params["max"]
return np.random.uniform(min, max, d)
def zeros_w(d_1, d, params):
return np.zeros((d_1, d))
def zeros_b(d, params):
return np.zeros(d)
def ones_w(d_1, d, params):
return np.ones((d_1, d))
def ones_b(d, params):
return np.ones(d)
順伝播、逆伝播
各関数は、パラメータにて受け渡しします。
# 順伝播
def propagation(layer, x, W, b, middle_func, middle_params, output_func, output_params):
u = {}
z = {}
# 入力層
z[0] = x
# 中間層
for i in range(1, layer):
u[i] = affine(z[i-1], W[i], b[i])
z[i] = middle_func(u[i], middle_params)
# 出力層
u[layer] = affine(z[layer-1], W[layer], b[layer])
y = output_func(u[layer], output_params)
return u, z, y
# 逆伝播
def back_propagation(layer, u, z, y, t, W, b, middle_back_func, middle_params, output_error_back_func):
du = {}
dz = {}
dW = {}
db = {}
# 出力層
du[layer] = output_error_back_func(y, u[layer], t)
dz[layer-1], dW[layer], db[layer] = affine_back(du[layer], z[layer-1], W[layer], b[layer])
# 中間層
for i in range(layer-1, 0, -1):
du[i] = middle_back_func(dz[i], u[i], z[i], middle_params)
dz[i-1], dW[i], db[i] = affine_back(du[i], z[i-1], W[i], b[i])
return du, dz, dW, db
学習
可変部分についてはパラメータ化しました。
入力層、出力層のノード数は、学習データのサイズから計算するようにしました。中間層のノード数のみ指定します。
後から検証できるように予測結果、重みとバイアスを返却するようにしまいた。また、エポックごとに表示している正解率、誤差も返却しています。
パラメータ一覧
| パラメータ | 既定値 | パラメータ値 |
|---|---|---|
| 中間層ノード数 | [100,50] | - |
| 重み初期化関数 | he_normal | lecun_normal,lecun_uniform, glorot_normal,glorot_uniform, he_normal,he_uniform, normal_w,uniform_w, zeros_w,ones_w |
| 重み初期化関数パラメータ | - | normal_wの場合、"mean"、"var" uniform_wの場合、"min"、"max" |
| バイアス初期化関数 | zeros_b | normal_b,uniform_b, zeros_b,ones_b |
| バイアス初期化関数パラメータ | - | normal_bの場合、"mean"、"var" uniform_bの場合、"min"、"max" |
| 学習率 | 0.1 | - |
| バッチサイズ | 100 | - |
| エポック数 | 50 | - |
| データ正規化関数 | min_max | min_max,z_score |
| データ正規化関数パラメータ | - | "axis":0、"axis":None |
| 中間層活性化関数 | relu | sigmoid,tanh,relu,leaky_relu, identity,softplus,softsign,step |
| 中間層活性化関数パラメータ | - | leaky_reluの場合、"alpha" |
| 出力層活性化関数 | softmax | softmax,identity |
| 出力層活性化関数パラメータ | - | - |
| 損失関数 | cross_entropy_error | mean_squared_error,cross_entropy_error |
# 学習
def learn(
name, # 学習識別名
x_train, # 学習データ
t_train, # 学習正解
x_test, # テストデータ
t_test, # テスト正解
md=[100, 50], # 中間層ノード数
weight_init_func=he_normal, # 重み初期化関数
weight_init_params={}, # 重み初期化関数パラメータ
bias_init_func=zeros_b, # バイアス初期化関数
bias_init_params={}, # バイアス初期化関数パラメータ
eta=0.1, # 学習率
batch_size=100, # バッチサイズ
epoch=50, # エポック数
data_norm_func=min_max, # データ正規化関数
data_norm_params={}, # データ正規化関数パラメータ
middle_func=relu, # 中間層活性化関数
middle_params={}, # 中間層活性化関数パラメータ
output_func=softmax, # 出力層活性化関数
output_params={}, # 出力層活性化関数パラメータ
error_func=cross_entropy_error # 損失関数
):
# 学習識別名表示
print(name)
# ノード数
d = [x_train.shape[x_train.ndim-1]] + md + [t_train.shape[t_train.ndim-1]]
# 階層数
layer = len(d) - 1
# 重み、バイアスの初期化
W = {}
b = {}
for i in range(layer):
W[i+1] = weight_init_func(d[i], d[i+1], weight_init_params)
for i in range(layer):
b[i+1] = bias_init_func(d[i+1], bias_init_params)
# 入力データの正規化
stats = {}
nx_train, train_stats = data_norm_func(x_train, stats, data_norm_params)
nx_test, test_stats = data_norm_func(x_test, train_stats, data_norm_params)
# 正解率、誤差初期化
train_rate = np.zeros(epoch+1)
test_rate = np.zeros(epoch+1)
train_err = np.zeros(epoch+1)
test_err = np.zeros(epoch+1)
# 勾配関数
middle_back_func = eval(middle_func.__name__ + "_back")
output_error_back_func = eval(output_func.__name__ + "_" + error_func.__name__ + "_back")
# 実行(学習データ)
u_train, z_train, y_train = propagation(layer, nx_train, W, b, middle_func, middle_params, output_func, output_params)
train_rate[0] = accuracy_rate(y_train, t_train)
train_err[0] = error_func(y_train, t_train)
# 実行(テストデータ)
u_test, z_test, y_test = propagation(layer, nx_test, W, b, middle_func, middle_params, output_func, output_params)
test_rate[0] = accuracy_rate(y_test, t_test)
test_err[0] = error_func(y_test, t_test)
# 正解率、誤差表示
print(" 学習データ正解率 = " + str(train_rate[0]) + " テストデータ正解率 = " + str(test_rate[0]) +
" 学習データ誤差 = " + str(train_err[0]) + " テストデータ誤差 = " + str(test_err[0]))
# 開始時刻設定
start_time = time.time()
for i in range(epoch):
# データのシャッフル(正解データも同期してシャフルする必要があるため一度、結合し分離)
nx_t = np.concatenate([nx_train, t_train], axis=1)
np.random.shuffle(nx_t)
nx, t = np.split(nx_t, [nx_train.shape[1]], axis=1)
for j in range(0, nx.shape[0], batch_size):
# 実行
u, z, y = propagation(layer, nx[j:j+batch_size], W, b, middle_func, middle_params, output_func, output_params)
# 勾配を計算
du, dz, dW, db = back_propagation(layer, u, z, y, t[j:j+batch_size], W, b, middle_back_func, middle_params, output_error_back_func)
# 重み、バイアスの調整
for k in range(1, layer+1):
W[k] = W[k] - eta*dW[k]
b[k] = b[k] - eta*db[k]
# 重み、バイアス調整後の実行(学習データ)
u_train, z_train, y_train = propagation(layer, nx_train, W, b, middle_func, middle_params, output_func, output_params)
train_rate[i+1] = accuracy_rate(y_train, t_train)
train_err[i+1] = error_func(y_train, t_train)
# 重み、バイアス調整後の実行(テストデータ)
u_test, z_test, y_test = propagation(layer, nx_test, W, b, middle_func, middle_params, output_func, output_params)
test_rate[i+1] = accuracy_rate(y_test, t_test)
test_err[i+1] = error_func(y_test, t_test)
# 正解率、誤差表示
print(str(i+1) + " 学習データ正解率 = " + str(train_rate[i+1]) + " テストデータ正解率 = " + str(test_rate[i+1]) +
" 学習データ誤差 = " + str(train_err[i+1]) + " テストデータ誤差 = " + str(test_err[i+1]))
# 終了時刻設定
end_time = time.time()
total_time = end_time - start_time
print("所要時間 = " +str(int(total_time/60))+" 分 "+str(int(total_time%60)) + " 秒")
return y_train, y_test, W, b, train_rate, train_err, test_rate, test_err, total_time
# クラスは利用しない方針で対応してきましたが、そろそろクラスの利用を考える必要があるかも
全体のプログラムは、最後に参考として載せています。
ランダムパラメータ実行
ノード数、学習率、バッチサイズをランダムに指定させました。ノード数は、大きくすると正解率が良くなることは分かっていましたが、ノード数を大きくすると計算量が多くなるため、100ノード以下としました。
活性化関数は、leaky_reluを利用します。$ \alpha $をパラメータで指定します。
| パラメータ | 既定値 | ランダム指定 |
|---|---|---|
| 中間層ノード数 | [100,50] | ノード数参照 |
| 1階層目のノード数 | 100 | 10~99 |
| 2階層目のノード数 | 50 | 10~99 |
| 重み初期化関数 | he_normal | ← |
| バイアス初期化関数 | zeros_b | ← |
| 学習率 | 0.1 | 0.005~0.5 |
| バッチサイズ | 100 | 10~90 |
| エポック数 | 50 | ← |
| データ正規化関数 | min_max | ← |
| 中間層活性化関数 | relu | leaky_relu |
| 中間層活性化関数パラメータ | - | "alpha":0.0~0.4 |
| 出力層活性化関数 | softmax | ← |
| 損失関数 | cross_entropy_error | ← |
実装
学習率は、対数で乱数を発生しました。
def random_log10(min, max):
min_log10 = np.log10(min)
max_log10 = np.log10(max)
rand = np.random.rand() * (max_log10-min_log10) + min_log10
return 10**rand
メインは、以下のように実装しました。
取得しない戻り値は、"_"を指定すればよいようです。ここでは、y_train, y_test, W, bは、取得しないため、以下のようにしています。
_, _, _, _, train_rates[i], train_errs[i], test_rates[i], test_errs[i], total_times[i] = learn(name[i],
x_train, t_train, x_test, t_test)
全体です。
# MNISTデータ読み込み
x_train, t_train, x_test, t_test = load_mnist('c:\\mnist\\')
# 結果格納変数定義
train_rates = {}
test_rates = {}
train_errs = {}
test_errs = {}
total_times = {}
# パラメータ格納得変数定義
name = {}
d1 = {}
d2 = {}
eta = {}
batch_size = {}
alpha = {}
# 100回実行
for i in range(100):
d1[i] = np.random.randint(10,100)
d2[i] = np.random.randint(10,100)
eta[i] = random_log10(0.005, 0.5)
batch_size[i] = np.random.randint(1,10)*10
alpha[i] = np.random.uniform(0.0, 0.4)
# 識別名
name[i]=str(i) + " d=[784," + str(d1[i]) + "," + str(d2[i]) + ",10] eta=" + str(eta[i]) + " batch_size=" + str(batch_size[i]) + " alpha=" + str(alpha[i])
# 学習
_, _, _, _, train_rates[i], train_errs[i], test_rates[i], test_errs[i], total_times[i] = learn(name[i],
x_train, t_train, x_test, t_test,
md=[d1[i], d2[i]], # ノード数
eta=eta[i], # 学習率
batch_size=batch_size[i], # バッチサイズ
middle_func=leaky_relu, # 中間層活性化関数
middle_params={"alpha":alpha[i]} # 中間層活性化関数パラメータ
)
結果
ベスト10を表にしました。
50エポック実行しましたが、今回は、各エポックの中で最高のテスト正解率を示します。また、その時のエポック数を示します。
| 順位 | 中間層ノード数 | 学習率 | バッチサイズ | leaky_relu | 最高テスト正解 | エポック数 |
|---|---|---|---|---|---|---|
| 1 | [93,42] | 0.302433213955 | 60 | 0.12512107 | 0.9829 | 28 |
| 2 | [79,50] | 0.45138265927 | 70 | 0.00961201 | 0.9822 | 35 |
| 3 | [98,73] | 0.336036375354 | 80 | 0.22205088 | 0.9812 | 23 |
| 4 | [86,73] | 0.0610066365149 | 20 | 0.09067058 | 0.9810 | 47 |
| 5 | [98,68] | 0.176085698986 | 80 | 0.29227329 | 0.9807 | 33 |
| 6 | [98,17] | 0.266984069679 | 80 | 0.21617011 | 0.9801 | 30 |
| 7 | [94,76] | 0.0988126904573 | 60 | 0.31976136 | 0.9799 | 41 |
| 8 | [65,61] | 0.0396461304998 | 30 | 0.00062834 | 0.9796 | 25 |
| 9 | [93,88] | 0.013555748156 | 20 | 0.06251875 | 0.9790 | 44 |
| 10 | [86,49] | 0.138111484307 | 90 | 0.05841015 | 0.9789 | 27 |
やはり、1階層目のノード数が多い場合が良い結果となりました。学習率は何とも言えません。
次に、ワースト10です。ただし、100回実行した内の13回は途中でオーバフローが発生し、最後まで学習できませんでした。オーバフローを除いたワーストです。
| 順位 | 中間層ノード数 | 学習率 | バッチサイズ | leaky_relu | 最高テスト正解 | エポック数 |
|---|---|---|---|---|---|---|
| 1 | [11,38] | 0.00799377305169 | 80 | 0.10308717 | 0.9419 | 47 |
| 2 | [10,33] | 0.360876335467 | 80 | 0.00512821 | 0.9436 | 49 |
| 3 | [10,46] | 0.0204809268382 | 90 | 0.37675387 | 0.9470 | 46 |
| 4 | [12,13] | 0.154481655964 | 60 | 0.3670397 | 0.9528 | 37 |
| 5 | [10,94] | 0.225053347204 | 80 | 0.0332154 | 0.953 | 37 |
| 6 | [15,14] | 0.174654717994 | 30 | 0.04042519 | 0.956 | 18 |
| 7 | [18,26] | 0.427977079413 | 90 | 0.05340576 | 0.9563 | 45 |
| 8 | [10,91] | 0.106041722932 | 40 | 0.35032192 | 0.9574 | 36 |
| 9 | [19,25] | 0.0925265723877 | 10 | 0.01006869 | 0.9603 | 31 |
| 10 | [13,61] | 0.0194410259578 | 40 | 0.28872271 | 0.9609 | 37 |
1階層目のノード数がすべて10台です。他の要素に比べてノード数の要因が大きいか、
ちなみに、オーバフローが発生したデータです。
| 中間層ノード数 | 学習率 | バッチサイズ | leaky_relu |
|---|---|---|---|
| [70,47] | 0.455120565919 | 40 | 0.390406 |
| [38,60] | 0.364510678024 | 20 | 0.3752583 |
| [11,15] | 0.410981255062 | 10 | 0.22906989 |
| [30,16] | 0.47312762974 | 10 | 0.16016474 |
| [49,72] | 0.153288885731 | 10 | 0.33473031 |
| [85,30] | 0.336504492399 | 10 | 0.0048215 |
| [24,55] | 0.364312295363 | 10 | 0.06023217 |
| [81,71] | 0.463112906631 | 40 | 0.23853512 |
| [49,73] | 0.481576312862 | 20 | 0.12823488 |
| [40,42] | 0.404546974262 | 70 | 0.32874793 |
| [60,27] | 0.413759964447 | 30 | 0.2589165 |
| [47,15] | 0.499725707964 | 70 | 0.32093298 |
| [54,98] | 0.326704994757 | 40 | 0.26140594 |
共通していることは、学習率が大きいことです。ただし、2位の学習率は0.45でした。何をきっかけにオーバーフローが発生しているのわかりません。
ランダムパラメータ実行2
前の実行では、ノード数の影響が大きかったため、ノード数は固定して実行します。
その代わりデータの正規化関数をmin_max,z_scoreで変更してみます。
| パラメータ | 既定値 | ランダム指定 |
|---|---|---|
| 中間層ノード数 | [100,50] | ← |
| 重み初期化関数 | he_normal | ← |
| バイアス初期化関数 | zeros_b | ← |
| 学習率 | 0.1 | 0.005~0.5 |
| バッチサイズ | 100 | 20~100 |
| エポック数 | 50 | ← |
| データ正規化関数 | min_max | min_max,z_score |
| データ正規化関数パラメータ | - | "axis":None,0 |
| 中間層活性化関数 | relu | leaky_relu |
| 中間層活性化関数パラメータ | - | "alpha":0.0~0.3 |
| 出力層活性化関数 | softmax | ← |
| 損失関数 | cross_entropy_error | ← |
実装
以下のように実装しました。
# MNISTデータ読み込み
x_train, t_train, x_test, t_test = load_mnist('c:\\mnist\\')
# 結果格納変数定義
train_rates = {}
test_rates = {}
train_errs = {}
test_errs = {}
total_times = {}
# パラメータ格納得変数定義
name = {}
d1 = {}
d2 = {}
eta = {}
batch_size = {}
alpha = {}
# 100回実行
for i in range(100):
data_norm = np.random.randint(1,5)
if data_norm == 1:
data_norm_func = min_max
data_norm_params = {"axis":None}
elif data_norm == 2:
data_norm_func = min_max
data_norm_params = {"axis":0}
elif data_norm == 3:
data_norm_func = z_score
data_norm_params = {"axis":None}
elif data_norm == 4:
data_norm_func = z_score
data_norm_params = {"axis":0}
eta[i] = random_log10(0.005, 0.5)
batch_size[i] = np.random.randint(2,11)*10
alpha[i] = np.random.uniform(0.0, 0.3)
# 識別名
name[i]=str(i) + " data_norm=" + str(data_norm) + " eta=" + str(eta[i]) + " batch_size=" + str(batch_size[i]) + " alpha=" + str(alpha[i])
# 学習
_, _, _, _, train_rates[i], train_errs[i], test_rates[i], test_errs[i], total_times[i] = learn(name[i],
x_train, t_train, x_test, t_test,
data_norm_func=data_norm_func, # データ正規化関数
data_norm_params=data_norm_params, # データ正規化関数パラメータ
eta=eta[i], # 学習率
batch_size=batch_size[i], # バッチサイズ
middle_func=leaky_relu, # 中間層活性化関数
middle_params={"alpha":alpha[i]} # 中間層活性化関数パラメータ
)
結果
テスト正解率が98%を超えたデータです。
| 順位 | 正規化関数 | 学習率 | バッチサイズ | leaky_relu | 最高テスト正解 | エポック数 |
|---|---|---|---|---|---|---|
| 1 | min_max(axis=None) | 0.0927278701741 | 20 | 0.09471167614945931 | 0.9838 | 37 |
| 2 | min_max(axis=None) | 0.214239714583 | 30 | 0.09976643519311072 | 0.9835 | 49 |
| 3 | min_max(axis=None) | 0.399621312108 | 70 | 0.16896605478656143 | 0.9826 | 47 |
| 4 | min_max(axis=0) | 0.378970024408 | 80 | 0.1391841049698662 | 0.9821 | 31 |
| 5 | min_max(axis=0) | 0.217384147336 | 30 | 0.0604149834408775 | 0.9820 | 47 |
| 6 | z_score(axis=None) | 0.0414183778921 | 30 | 0.03558674916729219 | 0.9816 | 47 |
| 7 | min_max(axis=None) | 0.268258601853 | 50 | 0.1438740580208833 | 0.9814 | 37 |
| 8 | z_score(axis=None) | 0.265386314508 | 100 | 0.14360062241900276 | 0.9810 | 25 |
| 9 | z_score(axis=None) | 0.0987836039477 | 40 | 0.03587081823860711 | 0.9806 | 49 |
| 10 | min_max(axis=None) | 0.186050959515 | 80 | 0.12623575288912603 | 0.9805 | 26 |
| 11 | min_max(axis=0) | 0.111506240912 | 60 | 0.05412096930493985 | 0.9804 | 39 |
| 11 | z_score(axis=None) | 0.202900552044 | 70 | 0.021710006625834655 | 0.9804 | 33 |
| 13 | z_score(axis=None) | 0.042169178054 | 20 | 0.04035340299593023 | 0.9803 | 28 |
| 14 | z_score(axis=None) | 0.183082207233 | 70 | 0.06608108085632532 | 0.9801 | 19 |
| 15 | min_max(axis=None) | 0.040402223936 | 30 | 0.27864566494599446 | 0.9801 | 49 |
| 16 | min_max(axis=None) | 0.0784329078478 | 40 | 0.23942583642707663 | 0.9800 | 32 |
| 16 | min_max(axis=None) | 0.0768888266807 | 50 | 0.0900024215022027 | 0.9800 | 49 |
学習率は、ある程度大きい方が良さそうです。今回も、学習率が大きいと、100回中14回オーバフローが発生しました。
学習率の大きい順に15個並べてみます。順位が×は、オーバフローが発生した回です。
| 順位 | 正規化関数 | 学習率 | バッチサイズ | leaky_relu | 最高テスト正解 | エポック数 |
|---|---|---|---|---|---|---|
| × | z_score(axis=0) | 0.493526468126 | 50 | 0.16302193208387158 | - | - |
| × | z_score(axis=None) | 0.493025438687 | 60 | 0.15257860986164548 | - | - |
| × | z_score(axis=0) | 0.457465751436 | 100 | 0.1833198975977736 | - | - |
| × | min_max(axis=0) | 0.438151737948 | 20 | 0.2226416317106006 | - | - |
| × | z_score(axis=0) | 0.427182859114 | 50 | 0.1775239627560666 | - | - |
| 3 | min_max(axis=None) | 0.399621312108 | 70 | 0.16896605478656143 | 0.9826 | 47 |
| 4 | min_max(axis=0) | 0.378970024408 | 80 | 0.1391841049698662 | 0.9821 | 31 |
| × | z_score(axis=None) | 0.327766842604 | 20 | 0.12409631412746923 | - | - |
| × | z_score(axis=0) | 0.327609746863 | 30 | 0.25360283198659694 | - | - |
| × | min_max(axis=0) | 0.311587718674 | 40 | 0.2771468518188593 | - | - |
| × | z_score(axis=0) | 0.302442036526 | 20 | 0.10774988623712077 | - | - |
| × | z_score(axis=0) | 0.292413067448 | 70 | 0.07117326944102596 | - | - |
| 7 | min_max(axis=None) | 0.268258601853 | 50 | 0.1438740580208833 | 0.9814 | 37 |
| 8 | z_score(axis=None) | 0.265386314508 | 100 | 0.14360062241900276 | 0.9810 | 25 |
オーバフローが発生する場合と発生しない場合の傾向がつかめません。
テスト正解率のワースト5です。
| 順位 | 正規化関数 | 学習率 | バッチサイズ | leaky_relu | 最高テスト正解 | エポック数 |
|---|---|---|---|---|---|---|
| 1 | min_max(axis=0) | 0.00553520035274 | 90 | 0.2681946146915237 | 0.9600 | 50 |
| 2 | min_max(axis=0) | 0.0050595537481 | 90 | 0.12487558139465842 | 0.9604 | 50 |
| 3 | min_max(axis=0) | 0.00696012106581 | 90 | 0.2483865324925018 | 0.9626 | 49 |
| 4 | min_max(axis=0) | 0.00666249586536 | 100 | 0.0020656761874577323 | 0.9649 | 49 |
| 5 | min_max(axis=0) | 0.00700526924433 | 90 | 0.2400293442668525 | 0.9654 | 49 |
これから言えることは、学習率が小さい&バッチサイズが大きいです。学習率が小さいとなかなか学習が進まない、ただし、バッチサイズを小さくすると学習率が小さくてっもある程度学習が進みます。
ランダムパラメータ実行3
学習率変更
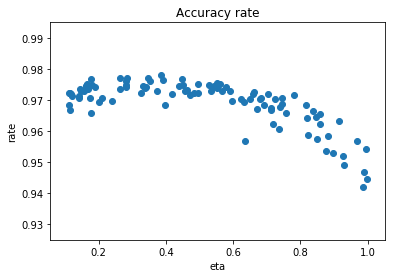
学習率を0.1~1.0にランダムに変更して実行してみました。活性化関数は、reluです。時間がかかるためエポック数は5にしました。
5エポック目のテスト正解率をグラフ化します。
学習率が0.2~0,4あたりが良い結果となりました。
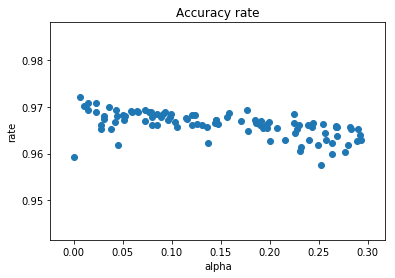
leaky_reluのalpha変更
学習率を0.1として、leaky_reluの$ \alpha $を0.0~0.3の間でランダムに変更してみます。エポック数は5です。
学習率が0.1の時は、$ \alpha $が0の方がよさそうです。
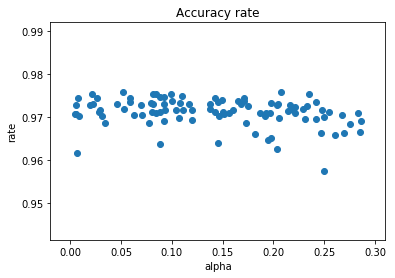
学習率を0.5に変更して実行してみました。
学習率を大きくしたため序盤の正解率は向上しました。
なお、ここまでの実行ではオーバフローは発生しませんでした。
オーバフロー
オーバフローを強制的に発生させるため、学習率を1.0、leaky_reluの$ \alpha $を0.1として実行しました。1エポック目のバッチ実行ごとに、u[3]、W[3]、dW[3]、dz[2]の最大値を表にします。
| No. | u[3] | W[3] | dW[3] | dz[2] |
|---|---|---|---|---|
| 1 | 1.02414694045 | 0.71142370528 | 0.103146812254 | 0.0556380289438 |
| 2 | 3.50086120607 | 0.717012777871 | 0.304204124963 | 0.0616197182729 |
| 3 | 42.0303510583 | 1.01637660155 | 9.19282549189 | 0.122515322953 |
| 4 | 187.486171612 | 2.5055810304 | 18.8419152026 | 1.06820299205 |
| 5 | 20979.4768888 | 6.79860594896 | 315.422922008 | 0.330265278138 |
| 6 | 1313582.06845 | 326.681196395 | 36853.335196 | 4.23711824052 |
| 7 | 807654175770.0 | 13940.1241538 | 19612923.7657 | 1680.74798761 |
| 8 | 2.09712899853e+22 | 7001210.14566 | 3.20687900685e+15 | 700478.542985 |
| 9 | 3.05664299541e+45 | 1.15197613201e+15 | 1.54566291385e+30 | 1.15197613094e+14 |
| 10 | 3.56936712336e+90 | 6.28215508137e+29 | 3.32250265958e+60 | 2.17387842199e+29 |
| 11 | 6.50199793932e+180 | 8.60638368111e+59 | 3.7355633174e+120 | 8.60638368111e+58 |
爆発的に大きな値になっています。
参考までに、学習率を1.0、reluの場合です。大きな値にはなりません。最終的にも大きな値とはなりません。
| No. | u[3] | W[3] | dW[3] | dz[2] |
|---|---|---|---|---|
| 1 | 1.13917149054 | 0.71142370528 | 0.115069014906 | 0.0562912992378 |
| 2 | 2.85198881448 | 0.710679074987 | 0.411644293618 | 0.0567578104152 |
| 3 | 43.2878534582 | 1.04498258635 | 10.9761589965 | 0.133511676772 |
| 4 | 2.97599151397 | 3.045657225 | 0.3944940876 | 1.1832955403 |
| 5 | 3.55269416732 | 3.045657225 | 0.697594957774 | 1.06049038113 |
| 6 | 3.46893146088 | 3.045657225 | 0.54347919221 | 0.613186155551 |
| 7 | 1.87653864759 | 3.045657225 | 0.188400250272 | 0.181941475396 |
| 8 | 6.61003329221 | 3.045657225 | 2.21060981208 | 0.100531181658 |
| 9 | 6.28065023901 | 3.045657225 | 0.472896096975 | 0.13147556295 |
| 10 | 1.8999663514 | 3.045657225 | 0.0873401782609 | 0.0868772615172 |
負の値に対するleaky_reluの勾配($ \alpha $=0.1)がここまで影響したのでしょうか、
今回は、ほとんど内容がありませんでした。次回は、過学習の対応を考えます。
参考
今回実行したプログラムの全体です。
import gzip
import numpy as np
# MNIST読み込み
def load_mnist( mnist_path ) :
return _load_image(mnist_path + 'train-images-idx3-ubyte.gz'), \
_load_label(mnist_path + 'train-labels-idx1-ubyte.gz'), \
_load_image(mnist_path + 't10k-images-idx3-ubyte.gz'), \
_load_label(mnist_path + 't10k-labels-idx1-ubyte.gz')
def _load_image( image_path ) :
# 画像データの読み込み
with gzip.open(image_path, 'rb') as f:
buffer = f.read()
size = np.frombuffer(buffer, np.dtype('>i4'), 1, offset=4)
rows = np.frombuffer(buffer, np.dtype('>i4'), 1, offset=8)
columns = np.frombuffer(buffer, np.dtype('>i4'), 1, offset=12)
data = np.frombuffer(buffer, np.uint8, offset=16)
image = np.reshape(data, (size[0], rows[0]*columns[0]))
image = image.astype(np.float32)
return image
def _load_label( label_path ) :
# 正解データ読み込み
with gzip.open(label_path, 'rb') as f:
buffer = f.read()
size = np.frombuffer(buffer, np.dtype('>i4'), 1, offset=4)
data = np.frombuffer(buffer, np.uint8, offset=8)
label = np.zeros((size[0], 10))
for i in range(size[0]):
label[i, data[i]] = 1
return label
# 正規化関数
def min_max(x, stats, params):
axis=params.get("axis")
if "min" not in stats:
stats["min"] = np.min(x, axis=axis, keepdims=True) # 最小値を求める
if "max" not in stats:
stats["max"] = np.max(x, axis=axis, keepdims=True) # 最大値を求める
return (x-stats["min"])/np.maximum((stats["max"]-stats["min"]),1e-7), stats
def z_score(x, stats, params):
axis=params.get("axis")
if "mean" not in stats:
stats["mean"] = np.mean(x, axis=axis, keepdims=True) # 平均値を求める
if "std" not in stats:
stats["std"] = np.std(x, axis=axis, keepdims=True) # 標準偏差を求める
return (x-stats["mean"])/np.maximum(stats["std"],1e-7), stats
# affine変換
def affine(z, W, b):
return np.dot(z, W) + b
def affine_back(du, z, W, b):
dz = np.dot(du, W.T) # zの勾配は、今までの勾配と重みを掛けた値
dW = np.dot(z.T, du) # 重みの勾配は、zに今までの勾配を掛けた値
size = 1
if z.ndim == 2:
size = z.shape[0]
db = np.dot(np.ones(size).T, du) # バイアスの勾配は、今までの勾配の値
return dz, dW, db
# 活性化関数(中間)
def sigmoid(u, params):
return 1/(1 + np.exp(-u))
def sigmoid_back(dz, u, z, params):
return dz * (z - z**2)
def tanh(u, params):
return np.tanh(u)
def tanh_back(dz, u, z, params):
return dz * (1/np.cosh(u)**2)
def relu(u, params):
return np.maximum(0, u)
def relu_back(dz, u, z, params):
return dz * np.where(u > 0, 1, 0)
def leaky_relu(u, params):
return np.maximum(u * params["alpha"], u)
def leaky_relu_back(dz, u, z, params):
return dz * np.where(u > 0, 1, params["alpha"])
def identity(u, params):
return u
def identity_back(dz, u, z, params):
return dz
def softplus(u, params):
return np.log(1+np.exp(u))
def softplus_back(dz, u, z, params):
return dz * (1/(1 + np.exp(-u)))
def softsign(u, params):
return u/(1+np.absolute(u))
def softsign_back(dz, u, z, params):
return dz * (1/(1+np.absolute(u))**2)
def step(u, params):
return np.where(u > 0, 1, 0)
def step_back(dz, u, x, params):
return 0
# 活性化関数(出力)
def softmax(u, params):
u = u.T
max_u = np.max(u, axis=0)
exp_u = np.exp(u - max_u)
sum_exp_u = np.sum(exp_u, axis=0)
y = exp_u/sum_exp_u
return y.T
# 損失関数
def mean_squared_error(y, t):
size = 1
if y.ndim == 2:
size = y.shape[0]
return 0.5 * np.sum((y-t)**2)/size
def cross_entropy_error(y, t):
size = 1
if y.ndim == 2:
size = y.shape[0]
return -np.sum(t * np.log(np.maximum(y,1e-7)))/size
#return -np.sum(t * np.log(y))/size
# 活性化関数(出力)+損失関数勾配
def softmax_cross_entropy_error_back(y, u, t):
size = 1
if y.ndim == 2:
size = y.shape[0]
return (y - t)/size
def identity_mean_squared_error_back(y, u, t):
size = 1
if y.ndim == 2:
size = y.shape[0]
return (y - t)/size
# 重み・バイアスの初期化
def lecun_normal(d_1, d, params):
var = 1/np.sqrt(d_1)
return np.random.normal(0, var, (d_1, d))
def lecun_uniform(d_1, d, params):
min = -np.sqrt(3/d_1)
max = np.sqrt(3/d_1)
return np.random.uniform(min, max, (d_1, d))
def glorot_normal(d_1, d, params):
var = np.sqrt(2/(d_1+d))
return np.random.normal(0, var, (d_1, d))
def glorot_uniform(d_1, d, params):
min = -np.sqrt(6/(d_1+d))
max = np.sqrt(6/(d_1+d))
return np.random.uniform(min, max, (d_1, d))
def he_normal(d_1, d, params):
var = np.sqrt(2/d_1)
return np.random.normal(0, var, (d_1, d))
def he_uniform(d_1, d, params):
min = -np.sqrt(6/d_1)
max = np.sqrt(6/d_1)
return np.random.uniform(min, max, (d_1, d))
def normal_w(d_1, d, params):
mean=0
var=1
if "mean" in params:
mean = params["mean"]
if "var" in params:
var = params["var"]
return np.random.normal(mean, var, (d_1, d))
def normal_b(d, params):
mean=0
var=1
if "mean" in params:
mean = params["mean"]
if "var" in params:
var = params["var"]
return np.random.normal(mean, var, d)
def uniform_w(d_1, d, params):
min=0
max=1
if "min" in params:
min = params["min"]
if "max" in params:
max = params["max"]
return np.random.uniform(min, max, (d_1, d))
def uniform_b(d, params):
min=0
max=1
if "min" in params:
min = params["min"]
if "max" in params:
max = params["max"]
return np.random.uniform(min, max, d)
def zeros_w(d_1, d, params):
return np.zeros((d_1, d))
def zeros_b(d, params):
return np.zeros(d)
def ones_w(d_1, d, params):
return np.ones((d_1, d))
def ones_b(d, params):
return np.ones(d)
# 正解率
def accuracy_rate(y, t):
max_y = np.argmax(y, axis=1)
max_t = np.argmax(t, axis=1)
return np.sum(max_y == max_t)/y.shape[0]
import numpy as np
import time
# 順伝播
def propagation(layer, x, W, b, middle_func, middle_params, output_func, output_params):
u = {}
z = {}
# 入力層
z[0] = x
# 中間層
for i in range(1, layer):
u[i] = affine(z[i-1], W[i], b[i])
z[i] = middle_func(u[i], middle_params)
# 出力層
u[layer] = affine(z[layer-1], W[layer], b[layer])
y = output_func(u[layer], output_params)
return u, z, y
# 逆伝播
def back_propagation(layer, u, z, y, t, W, b, middle_back_func, middle_params, output_error_back_func):
du = {}
dz = {}
dW = {}
db = {}
# 出力層
du[layer] = output_error_back_func(y, u[layer], t)
dz[layer-1], dW[layer], db[layer] = affine_back(du[layer], z[layer-1], W[layer], b[layer])
# 中間層
for i in range(layer-1, 0, -1):
du[i] = middle_back_func(dz[i], u[i], z[i], middle_params)
dz[i-1], dW[i], db[i] = affine_back(du[i], z[i-1], W[i], b[i])
return du, dz, dW, db
# 学習
def learn(
name, # 学習識別名
x_train, # 学習データ
t_train, # 学習正解
x_test, # テストデータ
t_test, # テスト正解
md=[100, 50], # 中間層ノード数
weight_init_func=he_normal, # 重み初期化関数
weight_init_params={}, # 重み初期化関数パラメータ
bias_init_func=zeros_b, # バイアス初期化関数
bias_init_params={}, # バイアス初期化関数パラメータ
eta=0.1, # 学習率
batch_size=100, # バッチサイズ
epoch=50, # エポック数
data_norm_func=min_max, # データ正規化関数
data_norm_params={}, # データ正規化関数パラメータ
middle_func=relu, # 中間層活性化関数
middle_params={}, # 中間層活性化関数パラメータ
output_func=softmax, # 出力層活性化関数
output_params={}, # 出力層活性化関数パラメータ
error_func=cross_entropy_error # 損失関数
):
# 学習識別名表示
print(name)
# ノード数
d = [x_train.shape[x_train.ndim-1]] + md + [t_train.shape[t_train.ndim-1]]
# 階層数
layer = len(d) - 1
# 重み、バイアスの初期化
W = {}
b = {}
for i in range(layer):
W[i+1] = weight_init_func(d[i], d[i+1], weight_init_params)
for i in range(layer):
b[i+1] = bias_init_func(d[i+1], bias_init_params)
# 入力データの正規化
stats = {}
nx_train, train_stats = data_norm_func(x_train, stats, data_norm_params)
nx_test, test_stats = data_norm_func(x_test, train_stats, data_norm_params)
# 正解率、誤差初期化
train_rate = np.zeros(epoch+1)
test_rate = np.zeros(epoch+1)
train_err = np.zeros(epoch+1)
test_err = np.zeros(epoch+1)
# 勾配関数
middle_back_func = eval(middle_func.__name__ + "_back")
output_error_back_func = eval(output_func.__name__ + "_" + error_func.__name__ + "_back")
# 実行(学習データ)
u_train, z_train, y_train = propagation(layer, nx_train, W, b, middle_func, middle_params, output_func, output_params)
train_rate[0] = accuracy_rate(y_train, t_train)
train_err[0] = error_func(y_train, t_train)
# 実行(テストデータ)
u_test, z_test, y_test = propagation(layer, nx_test, W, b, middle_func, middle_params, output_func, output_params)
test_rate[0] = accuracy_rate(y_test, t_test)
test_err[0] = error_func(y_test, t_test)
# 正解率、誤差表示
print(" 学習データ正解率 = " + str(train_rate[0]) + " テストデータ正解率 = " + str(test_rate[0]) +
" 学習データ誤差 = " + str(train_err[0]) + " テストデータ誤差 = " + str(test_err[0]))
# 開始時刻設定
start_time = time.time()
for i in range(epoch):
# データのシャッフル(正解データも同期してシャフルする必要があるため一度、結合し分離)
nx_t = np.concatenate([nx_train, t_train], axis=1)
np.random.shuffle(nx_t)
nx, t = np.split(nx_t, [nx_train.shape[1]], axis=1)
for j in range(0, nx.shape[0], batch_size):
# 実行
u, z, y = propagation(layer, nx[j:j+batch_size], W, b, middle_func, middle_params, output_func, output_params)
# 勾配を計算
du, dz, dW, db = back_propagation(layer, u, z, y, t[j:j+batch_size], W, b, middle_back_func, middle_params, output_error_back_func)
# 重み、バイアスの調整
for k in range(1, layer+1):
W[k] = W[k] - eta*dW[k]
b[k] = b[k] - eta*db[k]
# 重み、バイアス調整後の実行(学習データ)
u_train, z_train, y_train = propagation(layer, nx_train, W, b, middle_func, middle_params, output_func, output_params)
train_rate[i+1] = accuracy_rate(y_train, t_train)
train_err[i+1] = error_func(y_train, t_train)
# 重み、バイアス調整後の実行(テストデータ)
u_test, z_test, y_test = propagation(layer, nx_test, W, b, middle_func, middle_params, output_func, output_params)
test_rate[i+1] = accuracy_rate(y_test, t_test)
test_err[i+1] = error_func(y_test, t_test)
# 正解率、誤差表示
print(str(i+1) + " 学習データ正解率 = " + str(train_rate[i+1]) + " テストデータ正解率 = " + str(test_rate[i+1]) +
" 学習データ誤差 = " + str(train_err[i+1]) + " テストデータ誤差 = " + str(test_err[i+1]))
# 終了時刻設定
end_time = time.time()
total_time = end_time - start_time
print("所要時間 = " +str(int(total_time/60))+" 分 "+str(int(total_time%60)) + " 秒")
return y_train, y_test, W, b, train_rate, train_err, test_rate, test_err, total_time