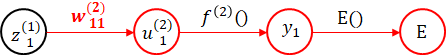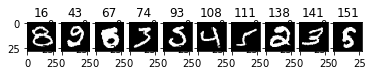今回は、学習の性能向上を試します。
改善案
前回は、重み、バイアスのひとつづつについて、入力から出力まで計算していました。MNISTでの計算回数は、以下でした。
1階層目:768 $ \times $ 50
2階層目:50 $ \times $ 100
3階層目:100 $ \times $ 10
ちょっと大きな値とちょっと小さい値の2回計算しているので2倍になります。
これを計算すると88,800回になります。
また、全データ60,000個分実行すると、5,328,000,000回実行になります。遅いわけです。
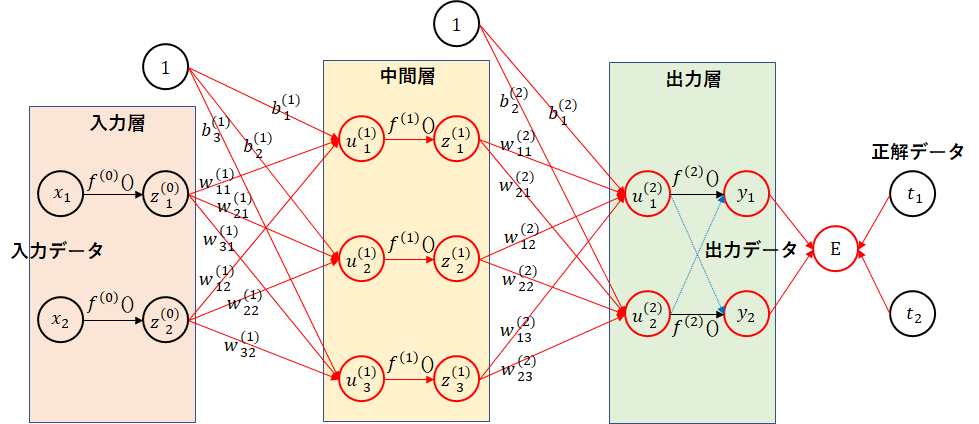
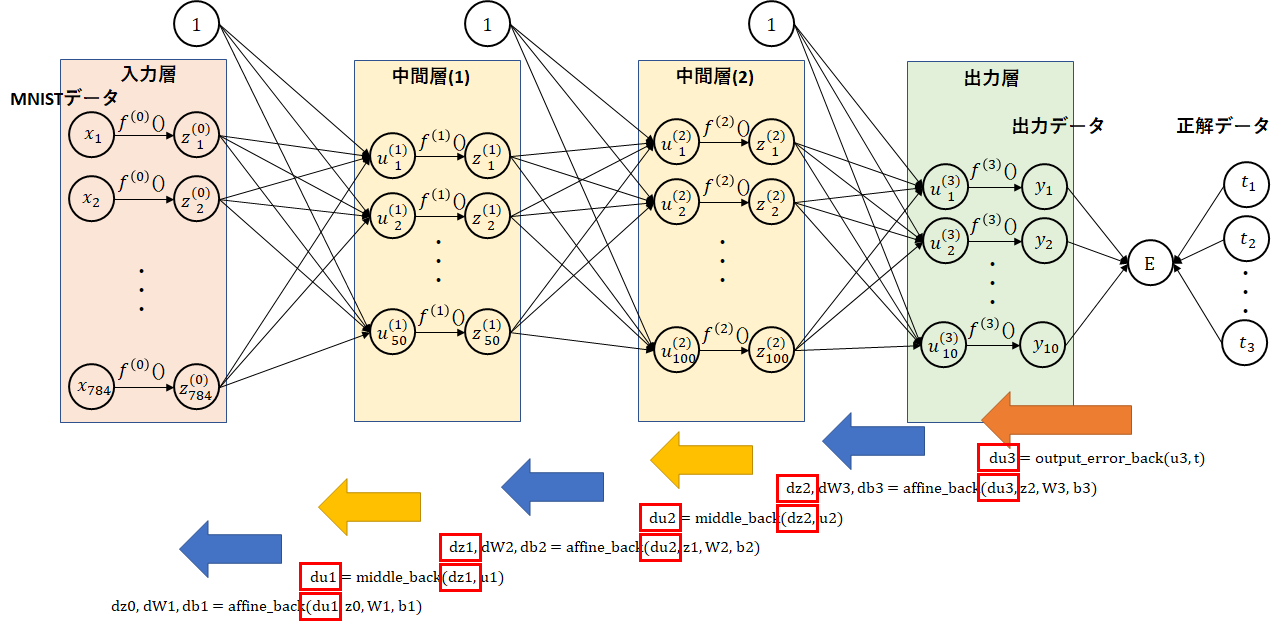
もう一度、ネットワーク図を見てみましょう。赤線の部分を全部計算しています。
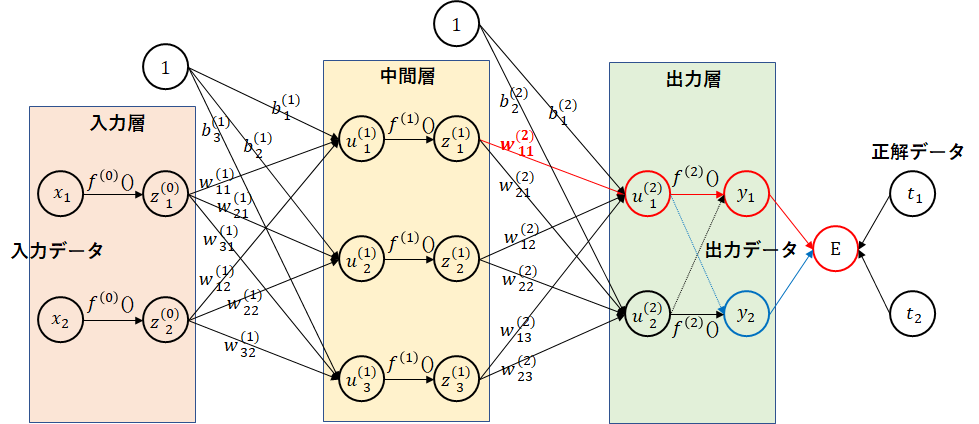
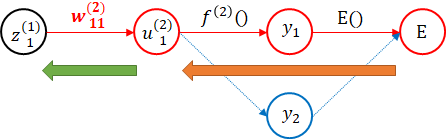
出力層の部分の$ w_{11}^{(2)} $に注目してみましょう。$ w_{11}^{(2)} $の変更が影響を及ぼすデータは、$ u_1^{(2)} $、$ y_1 $、$ E $のみになります。下図の赤線部分のみ計算し直せばよいことになります。
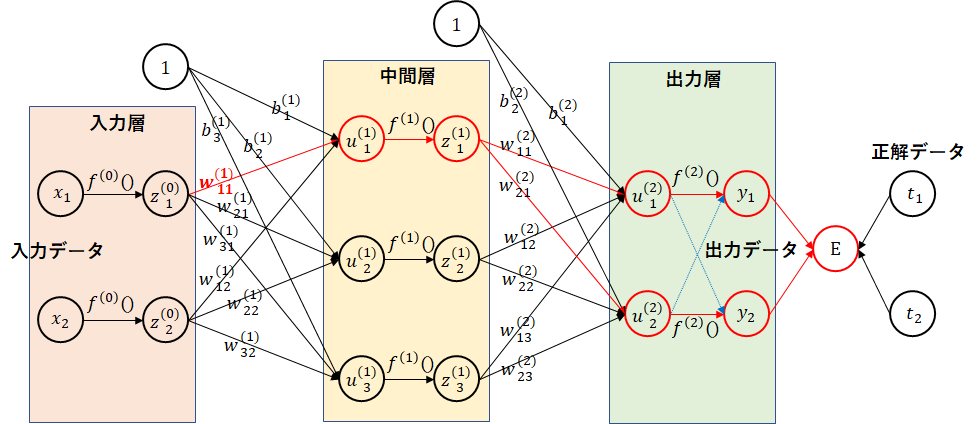
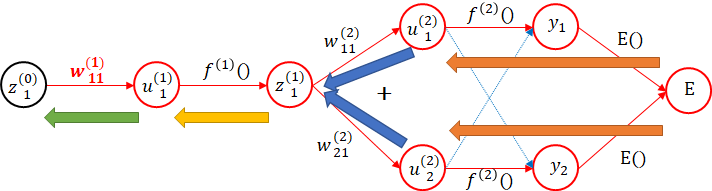
同様に、中間層の$ w_{11}^{(1)} $に注目してみましょう。$ w_{11}^{(2)} $の変更が影響を及ぼすデータは、$ u_1^{(1)} $、$ z_1^{(1)} $および以降はすべてになります。
赤線のみ計算すれば、かなり計算量が減ると思われます。
誤差逆伝播法
重み、バイアスに対する勾配をひとつひとつ計算していましたが、後で述べる2つの法則を利用すればもっと簡単に勾配の計算ができます。法則の詳細を簡単に説明できないかと考えたのですが難しいので、そんなものだと言う理解で使ってみましょう。もし、簡単に説明する方法が考えられれば、その際は更新します。
法則1:勾配は、ネットワークの各線の勾配の積となる。
下図で、$ w_{11}^{(2)} $について考えてみます。以下で勾配が計算できます。便宜上、後ろの矢印から書きます。
$ y_1 $の$ E() $に対する勾配 $ \times $ $ u_1^{(2)} $の$ f^{(2)}() $に対する勾配 $ \times $ $ w_{11}^{(2)} $の勾配
$ y_1 $の値をちょっと変化した場合の$ E $の変化、$ u_1^{(2)} $の値をちょっと変化した場合の$ y_1 $の変化、$ w_{11}^{(2)} $の値をちょっと変化した場合の$ u_1^{(2)} $の変化の積になります。
具体的に見ていきましょう。まずは出力層の部分です。
出力層の活性化関数には、softmax関数を利用しています。実は、$ u_1^{(2)} $を変化させると、$ y_2 $も変化します。ここは、オレンジの矢印の部分をまとめて対応することにしましょう。オレンジの矢印の部分の勾配を $ E^{'}(u_1^{(2)}) $ で表します。
E^{'}(u_1^{(2)}) = \frac{E(u_1^{(2)}+h) - E(u_1^{(2)}-h)}{2h}
次に、$ w_{11}^{(2)} $についてみてみましょう。
$ u_1^{(2)} = w_{11}^{(2)}z_1^{(1)}+w_{12}^{(2)}z_2^{(1)}+w_{13}^{(2)}z_3^{(1)}+b_1^{(2)} $ でした。勾配を計算してみます。
\frac{((w_{11}^{(2)}+h)z_1^{(1)}+w_{12}^{(2)}z_2^{(1)}+w_{13}^{(2)}z_3^{(1)}+b_1^{(2)}) - ((w_{11}^{(2)}-h)z_1^{(1)}+w_{12}^{(2)}z_2^{(1)}+w_{13}^{(2)}z_3^{(1)}+b_1^{(2)})}{2h} = z_1^{(1)}
緑の矢印部分は、$ z_1^{(1)} $になりました。
よって、$ w_{11}^{(2)} $に対する勾配は、以下の計算式になります。
z_1^{(1)} \times E^{'}(u_1^{(2)})
バイアス($ b_1^{(2)} $)についても見てみましょう。重み同様に計算してみます。
\frac{(w_{11}^{(2)}z_1^{(1)}+w_{12}^{(2)}z_2^{(1)}+w_{13}^{(2)}z_3^{(1)}+(b_1^{(2)}+h)) - (w_{11}^{(2)}z_1^{(1)}+w_{12}^{(2)}z_2^{(1)}+w_{13}^{(2)}z_3^{(1)}+(b_1^{(2)}-h))}{2h} = 1
1になりました。図でバイアスの矢印の元は、1でしたよね。
よって、$ b_1^{(2)} $に対する勾配は、以下の計算式になります。単に、オレンジの矢印の勾配になりました。
E^{'}(u_1^{(2)})
次に、中間層を見てみましょう。$ z_1^{(1)} $の部分で分岐しています。
ここで法則2を使います。
法則2:分岐の場合は、それぞれの勾配の和となる。
$ z_1^{(1)} $の$ w_{11}^{(2)} $方向の勾配を計算してみます。
\frac{(w_{11}^{(2)}(z_1^{(1)}+h)+w_{12}^{(2)}z_2^{(1)}+w_{13}^{(2)}z_3^{(1)}+b_1^{(2)}) - (w_{11}^{(2)}(z_1^{(1)}-h)+w_{12}^{(2)}z_2^{(1)}+w_{13}^{(2)}z_3^{(1)}+b_1^{(2)})}{2h} = w_{11}^{(2)}
同様に、$ w_{21}^{(2)} $方向は、$ w_{21}^{(2)} $になります。
よって、それぞれの青矢印、オレンジ矢印の勾配を掛けた値を加えればよいことになります。
w_{11}^{(2)} \times E^{'}(u_1^{(2)}) + w_{21}^{(2)} \times E^{'}(u_2^{(2)})
黄色の矢印は、$ f'^{(1)}(u_1^{(1)}) $となります。
f'^{(1)}(u_1^{(1)}) = \frac{f^{(1)}(u_1^{(1)}+h)-f^{(1)}(u_1^{(1)}-h)}{2h}
緑色の矢印は、出力層の際に計算したように、$ z_1^{(0)} $になります。
よって、$ w_{11}^{(1)} $に対する勾配は、以下の計算式になります。
z_1^{(0)} \times f'^{(1)}(u_1^{(1)}) \times (w_{11}^{(2)} \times E^{'}(u_1^{(2)}) + w_{21}^{(2)} \times E^{'}(u_2^{(2)}))
ここで注目して欲しいのは、後ろの勾配から順に前の勾配が計算できることです。矢印の勾配を1回求めるだけなので、大幅な性能改善が見込まれます。
実装
それでは、実装してみましょう。
まずは、出力層の$ E'(u) $の部分です。(オレンジ矢印の部分)
損失関数をerror_func、出力層の活性化関数をoutput_funcとします。
関数名は、output_error_backとしました。xの値のすこし大きな値と小さな値の出力層の活性化関数の値を計算し、その値を損失関数に渡します。そしてその差を計算して勾配を求めます。
def output_error_back(x, t):
h = 1e-4
dx = np.zeros(x.shape)
for idx,i in np.ndenumerate(x):
work = x[idx] # 現在の値を一時退避
x[idx] = work + h # すこし大きな値
y = output_func(x)
xph = error_func(y, t)
x[idx] = work - h # すこし小さな値
y = output_func(x)
xmh = error_func(y, t)
dx[idx] = (xph - xmh) / (2*h) # 勾配計算
x[idx] = work # 値をもとに戻す
return dx
次は、青矢印の部分です。重み、バイアスの勾配とともに、上位に返却する勾配を決めます。重みは、青矢印の部分(zの値)と、それまでの勾配を掛ければ求められました。バイアスも同様に青矢印の部分は、1なので結局、それまでの勾配になります。トータルの勾配は、それまでの勾配と重みを掛ければよいのでした。内積を利用して計算しています。
バイアスの部分は、ここでは複数データ処理できるように対応しています。1を掛ければよいのですが、データ件数分の1の配列を用意し、一度に計算できるようにしています。
def affine_back(dx, z, W, b):
dz = np.dot(dx, W.T) # zの勾配は、今までの勾配と重みを掛けた値
dW = np.dot(z.T, dx) # 重みの勾配は、zに今までの勾配を掛けた値
size = 1
if z.ndim == 2:
size = z.shape[0]
db = np.dot(np.ones(size).T, dx) # バイアスの勾配は、今までの勾配の値
return dz, dW, db
次に、黄色の矢印です。活性化関数をmiddle_funcとして勾配を計算します。すこし大きな値と小さな値から黄色矢印部分の勾配を求めて、いままでの勾配の値を掛けます。
def middle_back(dz, x):
h = 1e-4
work = x # 現在の値を一時退避
x = work + h # すこし大きな値
xph = middle_func(x)
x = work - h # すこし小さな値
xmh = middle_func(x)
du = (xph - xmh) / (2*h) # 勾配計算
x = work # 値をもとに戻す
return dz * du
これで、勾配の計算に必要な関数をすべて用意できました。
以下は、前回の勾配の計算です。
dW1 = calc_gradient(z0[i:i+batch_size], t[i:i+batch_size], W1)
db1 = calc_gradient(z0[i:i+batch_size], t[i:i+batch_size], b1)
dW2 = calc_gradient(z0[i:i+batch_size], t[i:i+batch_size], W2)
db2 = calc_gradient(z0[i:i+batch_size], t[i:i+batch_size], b2)
dW3 = calc_gradient(z0[i:i+batch_size], t[i:i+batch_size], W3)
db3 = calc_gradient(z0[i:i+batch_size], t[i:i+batch_size], b3)
今回は、以下のようになります。
du3 = output_error_back(u3[i:i+batch_size], t[i:i+batch_size])
dz2, dW3, db3 = affine_back(du3, z2[i:i+batch_size], W3, b3)
du2 = middle_back(dz2, u2[i:i+batch_size])
dz1, dW2, db2 = affine_back(du2, z1[i:i+batch_size], W2, b2)
du1 = middle_back(dz1, u1[i:i+batch_size])
dz0, dW1, db1 = affine_back(du1, z0[i:i+batch_size], W1, b1)
ちょっとわかりにくいかもしれませんが、後ろ側から順に勾配を求めて計算しています。求めた勾配を順に前に渡して計算していきます。
次に、今までの関数の見直しを行います。propagation関数は、途中のu,zの値を利用しますので返却するようにします。また、活性化関数を直接記述せず、定義を変更すればよいようにしました。
後は、各関数の定義です。正規化の関数もinit_funcとして定義するようにしました。
def propagation(x):
# 中間層(1)
u1 = affine(x, W1, b1)
z1 = middle_func(u1)
# 中間層(2)
u2 = affine(z1, W2, b2)
z2 = middle_func(u2)
# 出力層
u3 = affine(z2, W3, b3)
y = output_func(u3)
return u1, z1, u2, z2, u3, y
def init_func(x):
return min_max(x)
def middle_func(x):
return relu(x)
def output_func(x):
return softmax(x)
def error_func(y, t):
return cross_entropy_error(y, t)
誤差逆伝播法に対応したプログラムです。
今までに作成した関数群を先に読み込ませておく必要があります。一番下の(参考)にのせています。
import numpy as np
# ノード数
d0 = 784
d1 = 50
d2 = 100
d3 = 10
# 重み、バイアスの初期化、学習率、バッチサイズの設定
W1 = he_normal(d0,d1)
b1 = np.zeros(d1)
W2 = he_normal(d1,d2)
b2 = np.zeros(d2)
W3 = he_normal(d2,d3)
b3 = np.zeros(d3)
eta = 0.01
batch_size = 100
# MNISTデータ読み込み
x_train, t_train, x_test, t_test = load_mnist('c:\\mnist\\')
# 入力データの正規化
z0_train = init_func(x_train)
z0_test = init_func(x_test)
# データのシャッフル(正解データも同期してシャフルする必要があるため一度、結合し分離)
z0_t = np.concatenate([z0_train, t_train], axis=1)
np.random.shuffle(z0_t)
z0, t = np.split(z0_t, [z0_train.shape[1]], axis=1)
# 実行(学習データ)
u1_train, z1_train, u2_train, z2_train, u3_train, y_train = propagation(z0_train)
# 実行(テストデータ)
u1_test, z1_test, u2_test, z2_test, u3_test, y_test = propagation(z0_test)
# 正解率表示
print(" 学習データ正解率 = " + str(accuracy_rate(y_train, t_train)) + " テストデータ正解率 = " + str(accuracy_rate(y_test, t_test)))
for i in range(0,z0.shape[0],batch_size):
# 実行
u1, z1, u2, z2, u3, y = propagation(z0[i:i+batch_size])
# 勾配を計算
du3 = output_error_back(u3, t[i:i+batch_size])
dz2, dW3, db3 = affine_back(du3, z2, W3, b3)
du2 = middle_back(dz2, u2)
dz1, dW2, db2 = affine_back(du2, z1, W2, b2)
du1 = middle_back(dz1, u1)
dz0, dW1, db1 = affine_back(du1, z0[i:i+batch_size], W1, b1)
# 重み、バイアスの調整
W1 = W1 - eta*dW1
b1 = b1 - eta*db1
W2 = W2 - eta*dW2
b2 = b2 - eta*db2
W3 = W3 - eta*dW3
b3 = b3 - eta*db3
# 調整後の実行(学習データ)
u1_train, z1_train, u2_train, z2_train, u3_train, y_train = propagation(z0_train)
# 調整後の実行(テストデータ)
u1_test, z1_test, u2_test, z2_test, u3_test, y_test = propagation(z0_test)
print(str(i+1) + " ~ " + str(i+batch_size) + " 学習データ正解率 = " + str(accuracy_rate(y_train, t_train)) + " テストデータ正解率 = " + str(accuracy_rate(y_test, t_test)))
今回は、早く計算できました。
学習データ正解率 = 0.0955833333333 テストデータ正解率 = 0.0952
1 ~ 100 学習データ正解率 = 0.09895 テストデータ正解率 = 0.099
101 ~ 200 学習データ正解率 = 0.0994666666667 テストデータ正解率 = 0.0995
201 ~ 300 学習データ正解率 = 0.104983333333 テストデータ正解率 = 0.1053
301 ~ 400 学習データ正解率 = 0.10805 テストデータ正解率 = 0.1079
401 ~ 500 学習データ正解率 = 0.117133333333 テストデータ正解率 = 0.118
501 ~ 600 学習データ正解率 = 0.120283333333 テストデータ正解率 = 0.1201
601 ~ 700 学習データ正解率 = 0.124183333333 テストデータ正解率 = 0.1229
701 ~ 800 学習データ正解率 = 0.12895 テストデータ正解率 = 0.1272
801 ~ 900 学習データ正解率 = 0.133833333333 テストデータ正解率 = 0.1329
901 ~ 1000 学習データ正解率 = 0.14095 テストデータ正解率 = 0.1374
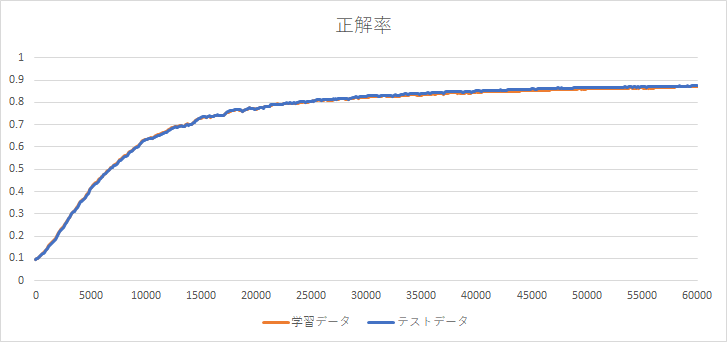
全データ、60,000件まで実行したグラフです。正解率が約87%まで達しました。
エポック
先ほどのグラフから、まだまだ正解率が向上しそうです。通常の学習は、1回だけでなく、同じデータで繰り返し学習するようです。すべての学習データを1回学習することをエポックと言います。MNISTであれば、60,000データの学習で1エポック、同じデータで再度学習し、2エポックになります。
複数エポックに対応したプログラムに修正します。指定したエポック数ループするようにしました。正解率は、エポックごとに求めます。
import numpy as np
# ノード数
d0 = 784
d1 = 50
d2 = 100
d3 = 10
# 重み、バイアスの初期化、学習率、バッチサイズ、エポックの設定
W1 = he_normal(d0,d1)
b1 = np.zeros(d1)
W2 = he_normal(d1,d2)
b2 = np.zeros(d2)
W3 = he_normal(d2,d3)
b3 = np.zeros(d3)
eta = 0.01
batch_size = 100
epoch = 10
# MNISTデータ読み込み
x_train, t_train, x_test, t_test = load_mnist('c:\\mnist\\')
# 入力データの正規化
z0_train = init_func(x_train)
z0_test = init_func(x_test)
# データのシャッフル(正解データも同期してシャフルする必要があるため一度、結合し分離)
z0_t = np.concatenate([z0_train, t_train], axis=1)
np.random.shuffle(z0_t)
z0, t = np.split(z0_t, [z0_train.shape[1]], axis=1)
# 実行(学習データ)
u1_train, z1_train, u2_train, z2_train, u3_train, y_train = propagation(z0_train)
# 実行(テストデータ)
u1_test, z1_test, u2_test, z2_test, u3_test, y_test = propagation(z0_test)
# 正解率表示
print(" 学習データ正解率 = " + str(accuracy_rate(y_train, t_train)) + " テストデータ正解率 = " + str(accuracy_rate(y_test, t_test)))
for j in range(epoch):
for i in range(0,z0.shape[0],batch_size):
# 実行
u1, z1, u2, z2, u3, y = propagation(z0[i:i+batch_size])
# 勾配を計算
du3 = output_error_back(u3, t[i:i+batch_size])
dz2, dW3, db3 = affine_back(du3, z2, W3, b3)
du2 = middle_back(dz2, u2)
dz1, dW2, db2 = affine_back(du2, z1, W2, b2)
du1 = middle_back(dz1, u1)
dz0, dW1, db1 = affine_back(du1, z0[i:i+batch_size], W1, b1)
# 重み、バイアスの調整
W1 = W1 - eta*dW1
b1 = b1 - eta*db1
W2 = W2 - eta*dW2
b2 = b2 - eta*db2
W3 = W3 - eta*dW3
b3 = b3 - eta*db3
# 調整後の実行(学習データ)
u1_train, z1_train, u2_train, z2_train, u3_train, y_train = propagation(z0_train)
# 調整後の実行(テストデータ)
u1_test, z1_test, u2_test, z2_test, u3_test, y_test = propagation(z0_test)
print(str(j+1) + " 学習データ正解率 = " + str(accuracy_rate(y_train, t_train)) + " テストデータ正解率 = " + str(accuracy_rate(y_test, t_test)))
実行結果です。10エポックで94%まで向上しました。
学習データ正解率 = 0.0955833333333 テストデータ正解率 = 0.0952
1 学習データ正解率 = 0.87225 テストデータ正解率 = 0.875
2 学習データ正解率 = 0.897233333333 テストデータ正解率 = 0.9015
3 学習データ正解率 = 0.909983333333 テストデータ正解率 = 0.9107
4 学習データ正解率 = 0.91795 テストデータ正解率 = 0.9182
5 学習データ正解率 = 0.924583333333 テストデータ正解率 = 0.9228
6 学習データ正解率 = 0.928983333333 テストデータ正解率 = 0.9281
7 学習データ正解率 = 0.932733333333 テストデータ正解率 = 0.9318
8 学習データ正解率 = 0.935916666667 テストデータ正解率 = 0.9357
9 学習データ正解率 = 0.938916666667 テストデータ正解率 = 0.9383
10 学習データ正解率 = 0.94125 テストデータ正解率 = 0.9409
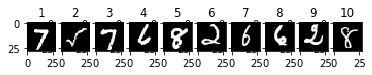
結果を見てみましょう。最初の10件の結果とその画像です。(MNISTの最初の10件ではなく、シャッフル後の最初の10件です。)各数字の出力結果$ y_i $を%で表示しています。正解は、太字です。
2番目以外は、正解でした。2番目は、1が約50%でした。正解は、5ですが、2番目の画像、5に見えますか?
| 数字 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.00 | 0.00 | 0.01 | 0.01 | 0.00 | 0.00 | 0.00 | 99.97 | 0.00 | 0.01 |
| 2 | 1.76 | 50.06 | 10.49 | 3.33 | 0.07 | 22.13 | 0.44 | 1.08 | 10.56 | 0.07 |
| 3 | 0.00 | 0.00 | 0.00 | 0.01 | 0.00 | 0.00 | 0.00 | 99.88 | 0.00 | 0.11 |
| 4 | 0.09 | 0.00 | 0.73 | 0.02 | 0.01 | 0.30 | 98.84 | 0.00 | 0.00 | 0.00 |
| 5 | 0.01 | 0.00 | 0.01 | 0.33 | 0.00 | 0.57 | 0.00 | 0.00 | 98.85 | 0.22 |
| 6 | 0.37 | 0.01 | 98.85 | 0.27 | 0.00 | 0.01 | 0.49 | 0.00 | 0.00 | 0.00 |
| 7 | 0.02 | 0.45 | 0.54 | 1.31 | 0.12 | 7.25 | 84.60 | 0.00 | 5.66 | 0.06 |
| 8 | 0.00 | 0.01 | 2.80 | 0.01 | 0.79 | 0.76 | 95.59 | 0.00 | 0.05 | 0.00 |
| 9 | 0.00 | 0.34 | 98.31 | 0.38 | 0.00 | 0.00 | 0.97 | 0.00 | 0.00 | 0.00 |
| 10 | 0.02 | 0.80 | 0.47 | 1.19 | 0.10 | 18.47 | 0.01 | 0.33 | 78.56 | 0.03 |
11件目以降で、不正解だった10件です。正解の数字を太字、正解と判断した数字をイタリックで示します。
特に43番目,67番目は、90%以降の確率で正解としていますが、不正解でした。43番目は、正解は2ですが、0と判断しました。67番目は、正解は5ですが、8と判断しました。これらの数字は、人の目でも、間違う人が多いのでは?
| 数字 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| 16 | 1.30 | 0.01 | 0.91 | 60.95 | 0.42 | 19.72 | 0.10 | 0.05 | 15.90 | 0.64 |
| 43 | 95.79 | 0.00 | 0.60 | 2.00 | 0.00 | 1.31 | 0.00 | 0.00 | 0.29 | 0.00 |
| 67 | 2.10 | 0.00 | 0.00 | 0.06 | 0.00 | 1.87 | 0.03 | 0.00 | 95.61 | 0.33 |
| 74 | 0.01 | 0.01 | 4.67 | 26.31 | 0.00 | 0.32 | 0.00 | 67.92 | 0.01 | 0.74 |
| 93 | 51.63 | 0.01 | 26.58 | 13.92 | 0.00 | 7.72 | 0.02 | 0.02 | 0.09 | 0.00 |
| 108 | 0.03 | 0.01 | 0.63 | 0.20 | 9.68 | 0.00 | 0.04 | 1.37 | 0.05 | 87.97 |
| 111 | 0.20 | 21.41 | 0.70 | 3.23 | 0.19 | 33.32 | 0.27 | 0.24 | 40.31 | 0.13 |
| 138 | 69.89 | 0.00 | 29.59 | 0.48 | 0.00 | 0.04 | 0.00 | 0.00 | 0.00 | 0.00 |
| 141 | 0.35 | 0.10 | 68.16 | 15.53 | 0.01 | 12.05 | 0.22 | 0.03 | 3.54 | 0.02 |
| 151 | 0.04 | 0.00 | 0.01 | 0.19 | 0.00 | 13.27 | 0.01 | 0.00 | 86.46 | 0.01 |
重み、バイアスの変化
先ほどの実行後の重み、バイアスの最小値、最大値、平均値を見てみましょう。
print('W1 最小値 = ' + str(np.min(W1)) + ' ([' + str(np.int(np.argmin(W1)/W1.shape[1])) + '][' + str(np.mod(np.argmin(W1),W1.shape[1])) + '])')
print('W1 平均値 = ' + str(np.mean(W1)))
print('W1 最大値 = ' + str(np.max(W1)) + ' ([' + str(np.int(np.argmax(W1)/W1.shape[1])) + '][' + str(np.mod(np.argmax(W1),W1.shape[1])) + '])')
print('W1 標準偏差 = ' + str(np.std(W1)))
print('b1 最小値 = ' + str(np.min(b1)) + ' ([' + str(np.argmin(b1)) + '])')
print('b1 平均値 = ' + str(np.mean(b1)))
print('b1 最大値 = ' + str(np.max(b1)) + ' ([' + str(np.argmax(b1)) + '])')
print('b1 標準偏差 = ' + str(np.std(b1)))
print('W2 最小値 = ' + str(np.min(W2)) + ' ([' + str(np.int(np.argmin(W2)/W2.shape[1])) + '][' + str(np.mod(np.argmin(W2),W2.shape[1])) + '])')
print('W2 平均値 = ' + str(np.mean(W2)))
print('W2 最大値 = ' + str(np.max(W2)) + ' ([' + str(np.int(np.argmax(W2)/W2.shape[1])) + '][' + str(np.mod(np.argmax(W2),W2.shape[1])) + '])')
print('W2 標準偏差 = ' + str(np.std(W2)))
print('b2 最小値 = ' + str(np.min(b2)) + ' ([' + str(np.argmin(b2)) + '])')
print('b2 平均値 = ' + str(np.mean(b2)))
print('b2 最大値 = ' + str(np.max(b2)) + ' ([' + str(np.argmax(b2)) + '])')
print('b2 標準偏差 = ' + str(np.std(b2)))
print('W3 最小値 = ' + str(np.min(W3)) + ' ([' + str(np.int(np.argmin(W3)/W3.shape[1])) + '][' + str(np.mod(np.argmin(W3),W3.shape[1])) + '])')
print('W3 平均値 = ' + str(np.mean(W3)))
print('W3 最大値 = ' + str(np.max(W3)) + ' ([' + str(np.int(np.argmax(W3)/W3.shape[1])) + '][' + str(np.mod(np.argmax(W3),W3.shape[1])) + '])')
print('W3 標準偏差 = ' + str(np.std(W3)))
print('b3 最小値 = ' + str(np.min(b3)) + ' ([' + str(np.argmin(b3)) + '])')
print('b3 平均値 = ' + str(np.mean(b3)))
print('b3 最大値 = ' + str(np.max(b3)) + ' ([' + str(np.argmax(b3)) + '])')
print('b3 標準偏差 = ' + str(np.std(b3)))
結果です。括弧内は、要素番号を表します。
結構、小さい値になっています。平均は、0に近いですね。
W1 最小値 = -0.215683681507 ([487][20])
W1 平均値 = 0.00289181066786
W1 最大値 = 0.226295371151 ([434][44])
W1 標準偏差 = 0.0537721940886
b1 最小値 = -0.080514889263 ([11])
b1 平均値 = 0.0250239727252
b1 最大値 = 0.141728276556 ([4])
b1 標準偏差 = 0.0499303977195
W2 最小値 = -0.834521381206 ([24][86])
W2 平均値 = 0.00318932553046
W2 最大値 = 0.828200612032 ([46][9])
W2 標準偏差 = 0.210507854251
b2 最小値 = -0.0903755259307 ([47])
b2 平均値 = 0.0136107723887
b2 最大値 = 0.121659228401 ([58])
b2 標準偏差 = 0.0323200998782
W3 最小値 = -0.67279333296 ([81][7])
W3 平均値 = 0.00255267426697
W3 最大値 = 0.584028052995 ([48][7])
W3 標準偏差 = 0.183865649512
b3 最小値 = -0.172679974526 ([8])
b3 平均値 = -6.52443168936e-10
b3 最大値 = 0.156593237942 ([5])
b3 標準偏差 = 0.080831611452
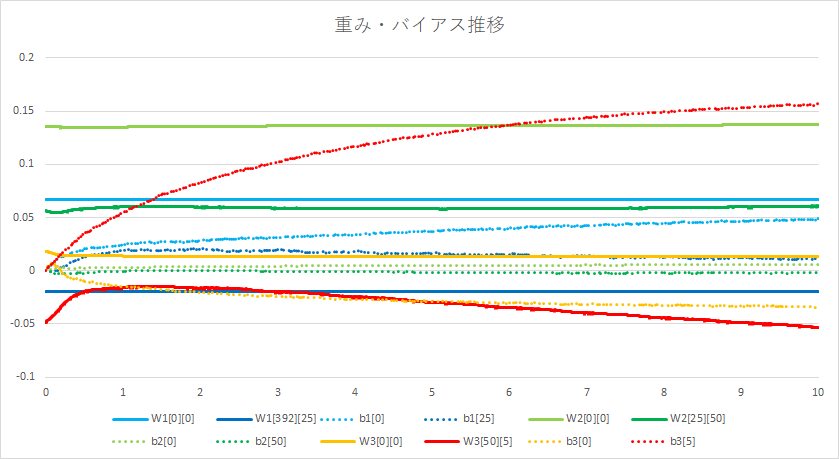
次に、重み、バイアスが、どのように変化したかをグラフに描いてみました。
以外と変化が少ないですね。グラフを描いてみましたが、この結果をどうとらえたらよいか、現時点ではわかりません。
しかし、実質数十ステップのプログラムで、ここまでできたことにびっくりです。しかも、数字でなくても、"○","△"、"×"でも、アルファベットでもロジックを変更せずに対応できてしまいます。
次回こそ、いろいろパラメータを変更して、試してみます。
(参考)
今までに作成した関数です。
import gzip
import numpy as np
def load_mnist( mnist_path ) :
return _load_image(mnist_path + 'train-images-idx3-ubyte.gz'), \
_load_label(mnist_path + 'train-labels-idx1-ubyte.gz'), \
_load_image(mnist_path + 't10k-images-idx3-ubyte.gz'), \
_load_label(mnist_path + 't10k-labels-idx1-ubyte.gz')
def _load_image( image_path ) :
# 画像データの読み込み
with gzip.open(image_path, 'rb') as f:
buffer = f.read()
size = np.frombuffer(buffer, np.dtype('>i4'), 1, offset=4)
rows = np.frombuffer(buffer, np.dtype('>i4'), 1, offset=8)
columns = np.frombuffer(buffer, np.dtype('>i4'), 1, offset=12)
data = np.frombuffer(buffer, np.uint8, offset=16)
image = np.reshape(data, (size[0], rows[0]*columns[0]))
image = image.astype(np.float32)
return image
def _load_label( label_path ) :
# 正解データ読み込み
with gzip.open(label_path, 'rb') as f:
buffer = f.read()
size = np.frombuffer(buffer, np.dtype('>i4'), 1, offset=4)
data = np.frombuffer(buffer, np.uint8, offset=8)
label = np.zeros((size[0], 10))
for i in range(size[0]):
label[i, data[i]] = 1
return label
def min_max(x, axis=None):
x_min = np.min(x, axis=axis, keepdims=True) # 最小値を求める
x_max = np.max(x, axis=axis, keepdims=True) # 最大値を求める
return (x-x_min)/np.maximum((x_max-x_min),1e-7)
def z_score(x, axis = None):
x_mean = np.mean(x, axis=axis, keepdims=True) # 平均値を求める
x_std = np.std(x, axis=axis, keepdims=True) # 標準偏差を求める
return (x-x_mean)/np.maximum(x_std,1e-7)
def affine(z, W, b):
return np.dot(z, W) + b
def sigmoid(x):
return 1/(1 + np.exp(-x))
def tanh(x):
return np.tanh(x)
def relu(x):
return np.maximum(0, x)
def identity(x):
return x
def softmax(x):
x = x.T
max_x = np.max(x, axis=0)
exp_x = np.exp(x - max_x)
sum_exp_x = np.sum(exp_x, axis=0)
y = exp_x/sum_exp_x
return y.T
def lecun_normal(d_1, d):
std = 1/np.sqrt(d_1)
return np.random.normal(0, std, (d_1, d))
def lecun_uniform(d_1, d):
min = -np.sqrt(3/d_1)
max = np.sqrt(3/d_1)
return np.random.uniform(min, max, (d_1, d))
def glorot_normal(d_1, d):
std = np.sqrt(2/(d_1+d))
return np.random.normal(0, std, (d_1, d))
def glorot_uniform(d_1, d):
min = -np.sqrt(6/(d_1+d))
max = np.sqrt(6/(d_1+d))
return np.random.uniform(min, max, (d_1, d))
def he_normal(d_1, d):
std = np.sqrt(2/d_1)
return np.random.normal(0, std, (d_1, d))
def he_uniform(d_1, d):
min = -np.sqrt(6/d_1)
max = np.sqrt(6/d_1)
return np.random.uniform(min, max, (d_1, d))
def mean_squared_error(y, t):
size = 1
if y.ndim == 2:
size = y.shape[0]
return 0.5 * np.sum((y-t)**2)/size
def cross_entropy_error(y, t):
size = 1
if y.ndim == 2:
size = y.shape[0]
return -np.sum(t * np.log(y))/size
def calc_gradient(x, t, w):
h = 1e-4
gradient = np.zeros(w.shape)
for idx,i in np.ndenumerate(w): # すべてのデータに対して実行
work = w[idx] # 現在の値を一時退避
w[idx] = work + h # すこし大きな値
yph = propagation(x)
eph = error_func(yph, t)
w[idx] = work - h # すこし小さな値
ymh = propagation(x)
emh = error_func(ymh, t)
gradient[idx] = (eph - emh) / (2*h) # 勾配計算
w[idx] = work # 値をもとに戻す
return gradient
def accuracy_rate(y, t):
max_y = np.argmax(y, axis=1)
max_t = np.argmax(t, axis=1)
return np.sum(max_y == max_t)/y.shape[0]
def affine_back(dx, z, W, b):
dz = np.dot(dx, W.T) # zの勾配は、今までの勾配と重みを掛けた値
dW = np.dot(z.T, dx) # 重みの勾配は、zに今までの勾配を掛けた値
size = 1
if z.ndim == 2:
size = z.shape[0]
db = np.dot(np.ones(size).T, dx) # バイアスの勾配は、今までの勾配の値
return dz, dW, db
def middle_back(dz, x):
h = 1e-4
work = x # 現在の値を一時退避
x = work + h # すこし大きな値
xph = middle_func(x)
x = work - h # すこし小さな値
xmh = middle_func(x)
du = (xph - xmh) / (2*h) # 勾配計算
x = work # 値をもとに戻す
return dz * du
def output_error_back(x, t):
h = 1e-4
dx = np.zeros(x.shape)
for idx,i in np.ndenumerate(x):
work = x[idx] # 現在の値を一時退避
x[idx] = work + h # すこし大きな値
y = output_func(x)
xph = error_func(y, t)
x[idx] = work - h # すこし小さな値
y = output_func(x)
xmh = error_func(y, t)
dx[idx] = (xph - xmh) / (2*h) # 勾配計算
x[idx] = work # 値をもとに戻す
return dx