ディープラーニングを実装から学ぶ（3）学習（勾配降下法）

今回は、学習について実装してみましょう。学習とは、重みとバイアスの調整になります。

#学習
何ごとにも目標を定め、現状を分析し、分析結果からどのように目標を達成するかを考えることが重要です。ディープラーニングでは、次のようになるのでしょうか、
　目標：出力データが正解データと一致する。（または、正解率XX%以上）
　現状：正解との乖離度合い（損失関数）を測定
　対策：乖離度合いを極力、少なくする。

損失関数

重みとバイアスの調整には、損失関数を利用します。損失関数は、正解との乖離度合いを表します。以下のような関数が利用されます。

二乗和誤差

出力データを$ y $、正解データを$ t $とし、各要素の差を2乗し合計した値。$ \frac{1}{2} $は、微分を考慮したものでここでは意味合いは無視しましょう。

E = \frac{1}{2}\sum_k(y_k-t_k)^2

import numpy as np
def mean_squared_error(y, t):
    return 0.5 * np.sum((y-t)**2)

交差エントロピー誤差

正解データに出力データの対数を掛けた値になります。正解データは、正解の要素のみ1であとは0のため、出力データの正解の要素に対して対数をとった値となります。

E= -\sum_kt_k\log{y_k}

import numpy as np
def cross_entropy_error(y, t):
    return -np.sum(t * np.log(y))

他にも、損失関数としては、出力データと正解データの差の絶対値など、いろいろあるようですが、ここでは、この２つを取り上げました。

前回のMNISTデータで試してみます。(1)でのload_mnist関数、(2)での各関数を利用しています。

import numpy as np
# ノード数
d0 = 784
d1 = 50
d2 = 100
d3 = 10
# 重み、バイアスの初期化
W1 = he_normal(d0,d1)
b1 = np.zeros(d1)
W2 = he_normal(d1,d2)
b2 = np.zeros(d2)
W3 = he_normal(d2,d3)
b3 = np.zeros(d3)
# MNISTデータ読み込み
x_train, t_train, x_test, t_test = load_mnist('c:\\mnist\\')
# 入力データの正規化
z0 = min_max(x_train)
# 中間層(1)
u1 = affine(z0[0], W1, b1)
z1 = relu(u1)
# 中間層(2)
u2 = affine(z1, W2, b2)
z2 = relu(u2)
# 出力層
u3 = affine(z2, W3, b3)
y = softmax(u3)

print(y)
print(t_train[0])
print(mean_squared_error(y, t_train[0]))
print(cross_entropy_error(y, t_train[0]))

[ 0.07801212  0.11621325  0.1715662   0.11645457  0.04418619  0.06040322
  0.16116579  0.08831403  0.11561257  0.04807207]
[ 0.  0.  0.  0.  0.  1.  0.  0.  0.  0.]
0.498416770065
2.80671291644

勾配

損失関数で求めた値をできるだけ小さくなるように、重み、バイアスを調整することが対策になります。
重み、バイアスの１つ１つをちょっと大きな値と小さい値にしてみます。それで損失関数の値がどのように変化するかを確認します。損失関数の値が小さくなる方が正解に近いことになります。以下のことが言えます。

　大きな値にした際の損失関数の値　＞　小さな値にした際の損失関数の値　→　小さな値にした方がよい。
　大きな値にした際の損失関数の値　＜　小さな値にした際の損失関数の値　→　大きな値にした方がよい。

重み、バイアスをちょっと大きい値にした際の損失関数の値から、ちょっと小さい値にした際の損失関数の値を引いて、区間で割った値が勾配になります。$ h $は、ちょっとの値になります。

E^{'}(w) = \frac{E(w+h) - E(w-h)}{2h}

勾配の計算は、出力データを計算する関数をpropagation()、誤差を計算する損失関数をerror()とすると、以下のようになります。$ w $は、重み、または、バイアスです。指定した重み、バイアスに対応する勾配の行列が返却されます。

import numpy as np
def calc_gradient(x, t, w):
    h = 1e-4
    gradient = np.zeros(w.shape)
    for idx,i in np.ndenumerate(w):     # すべてのデータに対して実行
        work = w[idx]                   # 現在の値を一時退避
        
        w[idx] = work + h               # すこし大きな値
        yph = propagation(x)
        eph = error_func(yph, t)
        
        w[idx] = work - h               # すこし小さな値
        ymh = propagation(x)
        emh = error_func(ymh, t)
        
        gradient[idx] = (eph - emh) / (2*h) # 勾配計算
        
        w[idx] = work                   # 値をもとに戻す
    return gradient

勾配降下法

重み、バイアスについては、求めた勾配を利用して以下のように更新します。

w = w - \eta E^{'}(w) 

$ E^{'} $が正の場合は、勾配のところで書いたように、重み、バイアスの値を小さくした方がよく、負の場合は大きくした方がよいですよね。そのため、重み、バイアスの値からマイナスします。$ \eta $は、学習率と言われており、どの程度更新するかを決めます。値が小さいとなかなか収束せず、大きいと振れ幅が大きくなるようです。

MNISTで、重み、バイアスの更新について考えてみましょう。
まずは、損失関数を複数データ同時に計算できるように対応します。今までのままだと、すべてのデータの和となってしまいますので、1データの誤差となるように、データ数で割ります。

import numpy as np
def mean_squared_error(y, t):
    size = 1
    if y.ndim == 2:
        size = y.shape[0]
    return 0.5 * np.sum((y-t)**2)/size
def cross_entropy_error(y, t):
    size = 1
    if y.ndim == 2:
        size = y.shape[0]
    return -np.sum(t * np.log(y))/size

もう1点、正解率を求める関数を事前に用意しておきましょう。出力データのうち最大の値のものと正解データが一致していると正解とみなします。どの程度の正解率になるか見ていきたいと思います。

import numpy as np
def accuracy_rate(y, t):
    max_y = np.argmax(y, axis=1)
    max_t = np.argmax(t, axis=1)
    return np.sum(max_y == max_t)/y.shape[0]

出力データを計算する関数をpropagation()、誤差を計算する損失関数をerror_func()を決めます。
propagation()は、データの正規化の部分は1度実行すればよいので含めていません。損失関数は、交差エントロピー誤差としました。

def propagation(x):
    # 中間層(1)
    u1 = affine(x, W1, b1)
    z1 = relu(u1)
    # 中間層(2)
    u2 = affine(z1, W2, b2)
    z2 = relu(u2)
    # 出力層
    u3 = affine(z2, W3, b3)
    y = softmax(u3)
    return y

def error_func(y, t):
    return cross_entropy_error(y, t)

それでは、MNISTで、学習することにより、どのように正解率が変わるか見ていきましょう。学習率は、0.01にしています。
重み、バイアスを調整し、再度、実行するようにしました。テストデータの正解率も確認しています。ただし、テストデータは学習には使ってはいけません。
今までに作成した関数群を先に読み込ませておく必要があります。一番下の(参考)にのせています。

import numpy as np
# ノード数
d0 = 784
d1 = 50
d2 = 100
d3 = 10
# 重み、バイアスの初期化、学習率の設定
W1 = he_normal(d0,d1)
b1 = np.zeros(d1)
W2 = he_normal(d1,d2)
b2 = np.zeros(d2)
W3 = he_normal(d2,d3)
b3 = np.zeros(d3)
eta = 0.01
# MNISTデータ読み込み
x_train, t_train, x_test, t_test = load_mnist('c:\\mnist\\')
# 入力データの正規化
z0_train = min_max(x_train)
z0_test  = min_max(x_test)

# 実行(学習データ)
y_train = propagation(z0_train)
# 実行(テストデータ)
y_test = propagation(z0_test)
# 正解率表示
print("学習データ正解率 = " + str(accuracy_rate(y_train, t_train)) + " テストデータ正解率 = " + str(accuracy_rate(y_test, t_test)))

# 勾配を計算
dW1 = calc_gradient(z0_train, t_train, W1)
db1 = calc_gradient(z0_train, t_train, b1)
dW2 = calc_gradient(z0_train, t_train, W2)
db2 = calc_gradient(z0_train, t_train, b2)
dW3 = calc_gradient(z0_train, t_train, W3)
db3 = calc_gradient(z0_train, t_train, b3)

# 重み、バイアスの調整
W1 = W1 - eta*dW1
b1 = b1 - eta*db1
W2 = W2 - eta*dW2
b2 = b2 - eta*db2
W3 = W3 - eta*dW3
b3 = b3 - eta*db3

# 調整後の実行(学習データ)
y_train = propagation(z0_train)
# 調整後の実行(テストデータ)
y_test = propagation(z0_test)
print("学習データ正解率 = " + str(accuracy_rate(y_train, t_train)) + " テストデータ正解率 = " + str(accuracy_rate(y_test, t_test)))

実行した結果、残念ながら私の非力なノートPCでは、しばらくしても結果が返ってきませんでした。途中で中断しました。
最初の正解率は表示されました。ほぼ、0.1です。ランダムに初期値を決めたため、1/10の確率で正解しています。未学習なので、当てずっぽうの確率と同じですね。

学習データ正解率 = 0.104283333333 テストデータ正解率 = 0.1085

確率的勾配降下法

先ほどのMNISTの例のように、全データから勾配を求め、重み、バイアスを調整する方法をバッチ学習と言います。しかし、データが多いと全データ分毎回計算することになり、なかなか学習が進みません。パワーのあるマシンであれば、MNISTデータであれば、十分かもしれませんが、ビッグデータでは難しいのではないでしょうか、
1データごとに勾配を求めて学習する方法をオンライン学習と言います。
その際の注意として、同じ正解の学習データが続かないように学習します。MNISTで言えば、0のデータばかり、学習し、次に1と順に学習せずに、ランダムに学習します。MNIST自体は、データはランダムのようですが、一応、並び替えを行います。

import numpy as np
# ノード数
d0 = 784
d1 = 50
d2 = 100
d3 = 10
# 重み、バイアスの初期化、学習率の設定
W1 = he_normal(d0,d1)
b1 = np.zeros(d1)
W2 = he_normal(d1,d2)
b2 = np.zeros(d2)
W3 = he_normal(d2,d3)
b3 = np.zeros(d3)
eta = 0.01
# MNISTデータ読み込み
x_train, t_train, x_test, t_test = load_mnist('c:\\mnist\\')
# 入力データの正規化
z0_train = min_max(x_train)
z0_test  = min_max(x_test)

# データのシャッフル(正解データも同期してシャフルする必要があるため一度、結合し分離)
z0_t = np.concatenate([z0_train, t_train], axis=1)
np.random.shuffle(z0_t)
z0, t = np.split(z0_t, [z0_train.shape[1]], axis=1)

# 実行(学習データ)
y = propagation(z0)
# 実行(テストデータ)
y_test = propagation(z0_test)
# 正解率表示
print(" 学習データ正解率 = " + str(accuracy_rate(y, t)) + " テストデータ正解率 = " + str(accuracy_rate(y_test, t_test)))

for i in range(z0.shape[0]):
    # 勾配を計算
    dW1 = calc_gradient(z0[i], t[i], W1)
    db1 = calc_gradient(z0[i], t[i], b1)
    dW2 = calc_gradient(z0[i], t[i], W2)
    db2 = calc_gradient(z0[i], t[i], b2)
    dW3 = calc_gradient(z0[i], t[i], W3)
    db3 = calc_gradient(z0[i], t[i], b3)

    # 重み、バイアスの調整
    W1 = W1 - eta*dW1
    b1 = b1 - eta*db1
    W2 = W2 - eta*dW2
    b2 = b2 - eta*db2
    W3 = W3 - eta*dW3
    b3 = b3 - eta*db3

    # 調整後の実行(学習データ)
    y = propagation(z0)
    # 調整後の実行(テストデータ)
    y_test = propagation(z0_test)
    print(str(i+1) + " 学習データ正解率 = " + str(accuracy_rate(y, t)) + " テストデータ正解率 = " + str(accuracy_rate(y_test, t_test)))

今度は、実行できました。しかし、かなり時間がかかります。

 学習データ正解率 = 0.0955833333333 テストデータ正解率 = 0.0952
1 学習データ正解率 = 0.100133333333 テストデータ正解率 = 0.0987
2 学習データ正解率 = 0.0922166666667 テストデータ正解率 = 0.0934
3 学習データ正解率 = 0.124133333333 テストデータ正解率 = 0.1245
4 学習データ正解率 = 0.1233 テストデータ正解率 = 0.1192
5 学習データ正解率 = 0.130683333333 テストデータ正解率 = 0.1257
6 学習データ正解率 = 0.134766666667 テストデータ正解率 = 0.1311
7 学習データ正解率 = 0.139333333333 テストデータ正解率 = 0.1323
8 学習データ正解率 = 0.151966666667 テストデータ正解率 = 0.1414
9 学習データ正解率 = 0.149366666667 テストデータ正解率 = 0.138
10 学習データ正解率 = 0.15165 テストデータ正解率 = 0.1394

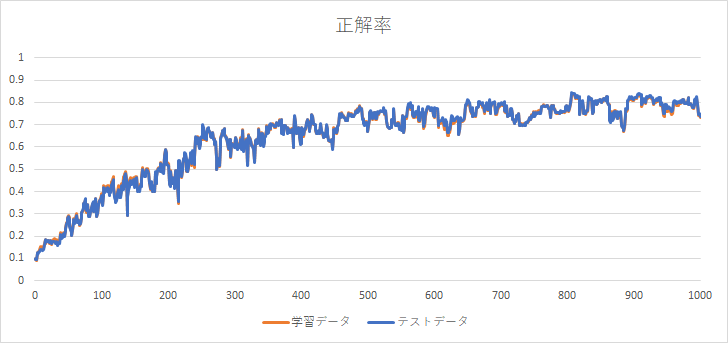
私の非力なノートPCで、約2時間半かけて1000件まで求めることができました。正解率のグラフを下に示します。正解率が徐々に向上していることが分かります。また、学習データの正解率に同期して、テストデータの正解率も向上しています。約80%の正解率になりました。この時点までは、順調に学習が進んでいるようです。

ミニバッチ

先ほどは、1件ごとに勾配の計算を行いました。時間がかかる上、対象の1件のデータに依存した学習になるため収束しにくくなるようです。一定のデータをまとめて学習する方法をミニバッチ学習と言います。10～100件程度の単位とするようです。
一部手直しを行います。

import numpy as np
# ノード数
d0 = 784
d1 = 50
d2 = 100
d3 = 10
# 重み、バイアスの初期化、学習率、バッチサイズの設定
W1 = he_normal(d0,d1)
b1 = np.zeros(d1)
W2 = he_normal(d1,d2)
b2 = np.zeros(d2)
W3 = he_normal(d2,d3)
b3 = np.zeros(d3)
eta = 0.01
batch_size = 100

# MNISTデータ読み込み
x_train, t_train, x_test, t_test = load_mnist('c:\\mnist\\')
# 入力データの正規化
z0_train = min_max(x_train)
z0_test  = min_max(x_test)

# データのシャッフル(正解データも同期してシャフルする必要があるため一度、結合し分離)
z0_t = np.concatenate([z0_train, t_train], axis=1)
np.random.shuffle(z0_t)
z0, t = np.split(z0_t, [z0_train.shape[1]], axis=1)

# 実行(学習データ)
y = propagation(z0)
# 実行(テストデータ)
y_test = propagation(z0_test)
# 正解率表示
print(" 学習データ正解率 = " + str(accuracy_rate(y, t)) + " テストデータ正解率 = " + str(accuracy_rate(y_test, t_test)))

for i in range(0, z0.shape[0], batch_size):
    # 勾配を計算
    dW1 = calc_gradient(z0[i:i+batch_size], t[i:i+batch_size], W1)
    db1 = calc_gradient(z0[i:i+batch_size], t[i:i+batch_size], b1)
    dW2 = calc_gradient(z0[i:i+batch_size], t[i:i+batch_size], W2)
    db2 = calc_gradient(z0[i:i+batch_size], t[i:i+batch_size], b2)
    dW3 = calc_gradient(z0[i:i+batch_size], t[i:i+batch_size], W3)
    db3 = calc_gradient(z0[i:i+batch_size], t[i:i+batch_size], b3)

    # 重み、バイアスの調整
    W1 = W1 - eta*dW1
    b1 = b1 - eta*db1
    W2 = W2 - eta*dW2
    b2 = b2 - eta*db2
    W3 = W3 - eta*dW3
    b3 = b3 - eta*db3

    # 調整後の実行(学習データ)
    y = propagation(z0)
    # 調整後の実行(テストデータ)
    y_test = propagation(z0_test)
    print(str(i+1) + " ～ " + str(i+batch_size) + " 学習データ正解率 = " + str(accuracy_rate(y, t)) + " テストデータ正解率 = " + str(accuracy_rate(y_test, t_test)))

バッチサイズを100として実行してみます。

 学習データ正解率 = 0.0955833333333 テストデータ正解率 = 0.0952
1 ～ 100 学習データ正解率 = 0.09895 テストデータ正解率 = 0.099
101 ～ 200 学習データ正解率 = 0.0994666666667 テストデータ正解率 = 0.0995
201 ～ 300 学習データ正解率 = 0.105 テストデータ正解率 = 0.1053
301 ～ 400 学習データ正解率 = 0.10795 テストデータ正解率 = 0.1079
401 ～ 500 学習データ正解率 = 0.117066666667 テストデータ正解率 = 0.118
501 ～ 600 学習データ正解率 = 0.120183333333 テストデータ正解率 = 0.12
601 ～ 700 学習データ正解率 = 0.124133333333 テストデータ正解率 = 0.1229
701 ～ 800 学習データ正解率 = 0.128916666667 テストデータ正解率 = 0.1272
801 ～ 900 学習データ正解率 = 0.133816666667 テストデータ正解率 = 0.133
901 ～ 1000 学習データ正解率 = 0.140883333333 テストデータ正解率 = 0.1374

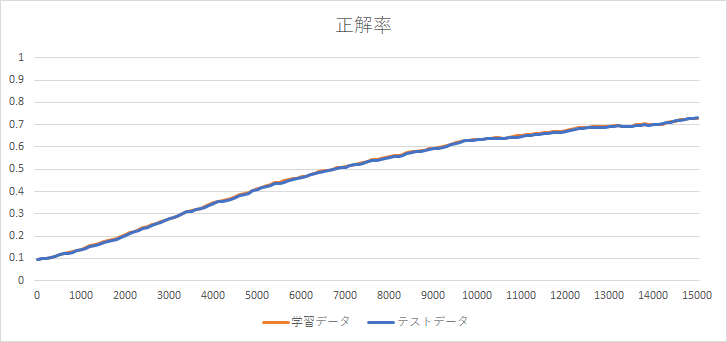
15000データまで、実行してみました。下のグラフのように、徐々に正解率が向上するグラフになりました。もう少し続けるともっと正解率が向上しそうですが、時間がかかるため中断しました。

数字の形状を教えているわけではないですが、正解率が向上しています。不思議ですね。
ただし、このままだと、時間がかかりすぎて使い物になりません。次回は、もっと、高速に実行する方法を検討します。本当は、今回、いろいろパラメータを変更して試してみたかったのですが次回にします。

(参考)
今までに作成した関数です。

import gzip
import numpy as np
def load_mnist( mnist_path ) :
    return _load_image(mnist_path + 'train-images-idx3-ubyte.gz'), \
           _load_label(mnist_path + 'train-labels-idx1-ubyte.gz'), \
           _load_image(mnist_path + 't10k-images-idx3-ubyte.gz'), \
           _load_label(mnist_path + 't10k-labels-idx1-ubyte.gz')
def _load_image( image_path ) :
    # 画像データの読み込み
    with gzip.open(image_path, 'rb') as f:
        buffer = f.read()
    size = np.frombuffer(buffer, np.dtype('>i4'), 1, offset=4)
    rows = np.frombuffer(buffer, np.dtype('>i4'), 1, offset=8)
    columns = np.frombuffer(buffer, np.dtype('>i4'), 1, offset=12)
    data = np.frombuffer(buffer, np.uint8, offset=16)
    image = np.reshape(data, (size[0], rows[0]*columns[0]))
    image = image.astype(np.float32)
    return image
def _load_label( label_path ) :
    # 正解データ読み込み
    with gzip.open(label_path, 'rb') as f:
        buffer = f.read()
    size = np.frombuffer(buffer, np.dtype('>i4'), 1, offset=4)
    data = np.frombuffer(buffer, np.uint8, offset=8)
    label = np.zeros((size[0], 10))
    for i in range(size[0]):
        label[i, data[i]] = 1
    return label

def min_max(x, axis=None):
    x_min = np.min(x, axis=axis, keepdims=True) # 最小値を求める
    x_max = np.max(x, axis=axis, keepdims=True) # 最大値を求める
    return (x-x_min)/np.maximum((x_max-x_min),1e-7)

def z_score(x, axis = None):
    x_mean = np.mean(x, axis=axis, keepdims=True) # 平均値を求める
    x_std  = np.std(x, axis=axis, keepdims=True)  # 標準偏差を求める
    return (x-x_mean)/np.maximum(x_std,1e-7)

def affine(z, W, b):
    return np.dot(z, W) + b

def sigmoid(x):
    return 1/(1 + np.exp(-x))

def tanh(x):
    return np.tanh(x)

def relu(x):
    return np.maximum(0, x)

def identity(x):
    return x

def softmax(x):
    x = x.T
    max_x = np.max(x, axis=0)
    exp_x = np.exp(x - max_x)
    sum_exp_x = np.sum(exp_x, axis=0)
    y = exp_x/sum_exp_x
    return y.T

def lecun_normal(d_1, d):
    std = 1/np.sqrt(d_1)
    return np.random.normal(0, std, (d_1, d))
def lecun_uniform(d_1, d):
    min = -np.sqrt(3/d_1)
    max = np.sqrt(3/d_1)
    return np.random.uniform(min, max, (d_1, d))

def glorot_normal(d_1, d):
    std = np.sqrt(2/(d_1+d))
    return np.random.normal(0, std, (d_1, d))
def glorot_uniform(d_1, d):
    min = -np.sqrt(6/(d_1+d))
    max = np.sqrt(6/(d_1+d))
    return np.random.uniform(min, max, (d_1, d))

def he_normal(d_1, d):
    std = np.sqrt(2/d_1)
    return np.random.normal(0, std, (d_1, d))
def he_uniform(d_1, d):
    min = -np.sqrt(6/d_1)
    max = np.sqrt(6/d_1)
    return np.random.uniform(min, max, (d_1, d))

def mean_squared_error(y, t):
    size = 1
    if y.ndim == 2:
        size = y.shape[0]
    return 0.5 * np.sum((y-t)**2)/size
def cross_entropy_error(y, t):
    size = 1
    if y.ndim == 2:
        size = y.shape[0]
    return -np.sum(t * np.log(y))/size

def calc_gradient(x, t, w):
    h = 1e-4
    gradient = np.zeros(w.shape)
    for idx,i in np.ndenumerate(w):     # すべてのデータに対して実行
        work = w[idx]                   # 現在の値を一時退避
        
        w[idx] = work + h               # すこし大きな値
        yph = propagation(x)
        eph = error_func(yph, t)
        
        w[idx] = work - h               # すこし小さな値
        ymh = propagation(x)
        emh = error_func(ymh, t)
        
        gradient[idx] = (eph - emh) / (2*h) # 勾配計算
        
        w[idx] = work                   # 値をもとに戻す
    return gradient

def accuracy_rate(y, t):
    max_y = np.argmax(y, axis=1)
    max_t = np.argmax(t, axis=1)
    return np.sum(max_y == max_t)/y.shape[0]