LoginSignup
9
12

More than 5 years have passed since last update.

@Nezura

ディープラーニングを実装から学ぶ～ (まとめ２）しかし、繊細

Last updated at Posted at 2018-05-06

前回は、実装は簡単と書きましたが、学習の呼び出し部分を説明しませんでした。実は、学習のためのパラメータ（ハイパーパラメータ）の決定は難しいです。

データの前処理

学習用に利用しているMNISTでは、問題ありませんが、実データでは、欠測値、異常値、ノイズが含まれいる可能性があります。
欠測値が存在する場合の対応を考える必要があります。対応例です。

  • 欠測値を含むデータを利用しない
  • 欠測値を含む項目を利用しない
  • 欠測値を何らかの値で補完する。中央値、平均値、他のデータから推測する方法などがあります。

異常値、ノイズについても事前に対応方法の検討が必要です。

また、文字データでは学習できないため、数値データに変換する必要があります。例えば、ダミー変数化を行います。

正規化・標準化

例えば、気象データを考えた場合、気温、降水量、風速、気圧など、取りうる値の範囲や分布が異なります。事前にデータの桁数やばらつきを揃えます。

正規化

データを0～1,-1～1などとなるように変換をします。
今回のMNISTデータでは、0～255のデータを0～1に変換しています。

標準化

ばらつきを均一にするため、平均0、分散1などとなるようにデータを変換します。

ハイパーパラメータ

以下のパラメータを決定する必要があります。

中間層の数、ノード数

層の数をいくつにするか、各層のノード数をいくつにするか決定する必要があります。
層を深くすればするほど良いわけれはなく、ノード数を多くすれば良いわけでもありません。
後で試してみます。

学習率

学習率を大きくすると序盤は学習が早く進みますが、なかなか収束しません。逆に、学習率を小さくすると学習がなかなか進みません。

バッチサイズ

学習ごとのデータ数を決めます。全データをまとめて学習するバッチ学習、１データごと学習するオンライン学習がありますが、通常は、一定のデータをまとめて学習を行うミニバッチ学習で行います。
ミニバッチの際には、毎回乱数を利用し学習データを選択します。MNISTは、データが元々ランダムに並んでいるため、データ順に学習しました。

エポック

データを何回学習するかを決定します。学習すればするほど良いというものではありません。学習データの正解率は高くなりますが、テストデータの正解率は高くなるとは限りません。特に、過学習を起こし、逆に、テストデータの正解率が下がることもあります。
時間的な制約もありますので適度で打ち切る必要があります。

重み、バイアスの初期値

重み、バイアスの初期値を決めます。特に重みの初期値は、定数を指定すると学習が進みません。一般的には、乱数を用いて初期値を決めます。一方、バイアスの初期値は、0が一般的なようです。
最適な値は、ノード数や活性化関数などにより異なります。活性化関数がReLUの際には、Heの初期値が良いようです。
詳細は、以下に記載しています。

「ディープラーニングを実装から学ぶ（２）ニューラルネットワーク」重み、バイアスの初期値
「ディープラーニングを実装から学ぶ（5）学習（パラメータ調整）」重みの初期値

活性化関数、損失関数

中間層の活性化関数は、ReLUを利用しましたが、他にもいろいろな関数があります。詳細は、以下に記載しています。

「ディープラーニングを実装から学ぶ（２）ニューラルネットワーク」活性化関数
「ディープラーニングを実装から学ぶ（5）学習（パラメータ調整）」活性化関数(中間層)

出力層の活性化関数は、ソフトマックス関数としています。損失関数は、交差エントロピー誤差としています。今回は、それぞれの関数を固定として試します。

実装変更

前回は、分かりやすくするために、中間層２層固定の実装にしました。層数を変更できるように変更します。と言ってもforループにするだけです。

学習

def learn(x, t, W, b, lr):
    # 層数
    layer = len(W)
    # 順伝播
    u = {}
    z = {}
    z[0] = x
    for i in range(1, layer):
        u[i] = affine(z[i-1], W[i], b[i])
        z[i] = relu(u[i])
    u[layer] = affine(z[layer-1], W[layer], b[layer])
    y  = softmax(u[layer])
    # 逆伝播
    dz = {}
    du = {}
    dW = {}
    db = {}
    du[layer] = softmax_cross_entropy_error_back(y, t)
    dz[layer-1], dW[layer], db[layer] = affine_back(du[layer], z[layer-1], W[layer], b[layer])
    for i in range(layer-1, 0, -1):
        du[i] = relu_back(dz[i], u[i])
        dz[i-1], dW[i], db[i] = affine_back(du[i], z[i-1], W[i], b[i])
    # 重み、バイアスの更新
    for i in range(1, layer+1):
        W[i] = W[i] - lr * dW[i]
        b[i] = b[i] - lr * db[i]
    return W, b

予測

def predict(x, W, b):
    # 層数
    layer = len(W) 
    # 順伝播
    u = {}
    z = {}
    z[0] = x
    for i in range(1, layer):
        u[i] = affine(z[i-1], W[i], b[i])
        z[i] = relu(u[i])
    u[layer] = affine(z[layer-1], W[layer], b[layer])
    y  = softmax(u[layer])
    return y

乱数の影響

重みの初期値とともに通常は、データをシャッフルのため乱数を利用します。MNISTでは、もともとデータがシャッフルされていますので、シャッフルしていませんでした。
２つの乱数のseed値を変更して試してみます。

重みの初期値、シャッフルのseed値を1～10まで変更して試してみます。

import numpy as np
import time

train_rates = {}
test_rates = {}
train_errs = {}
test_errs = {}
total_times = {}

# MNISTデータ読み込み
x_train, t_train, x_test, t_test = load_mnist('c:\\mnist\\')

# 入力データの正規化(0～1)
nx_train = x_train/255
nx_test  = x_test/255

# 学習回数
epoch = 50
# ノード数
md = [100,50]
# 学習率
lr = 0.5
# バッチサイズ
batch_size = 100

for m in range(10):
    # 学習データシャッフル
    np.random.seed(m+1)
    # データのシャッフル(正解データも同期してシャフルする必要があるため一度、結合し分離)
    nx_t = np.concatenate([nx_train, t_train], axis=1)
    np.random.shuffle(nx_t)
    nx, t = np.split(nx_t, [nx_train.shape[1]], axis=1)
    sx_train = nx
    st_train  = t

    for n in range(10):
        d = [nx_train.shape[1]] + md + [10] 
        name = "xseed=" + str(m+1) + " Wseed=" + str(n+1)
        print(name)

        # 重みの初期化(-0.1～0.1の乱数)、バイアスの初期化(0)
        W = {}
        b = {}
        np.random.seed(n+1)
        for i in range(1, len(d)):
            W[i] = np.random.rand(d[i-1], d[i]) * 0.2 - 0.1
            b[i] = np.zeros(d[i])

        train_rate, train_err = np.zeros(epoch+1), np.zeros(epoch+1)
        test_rate, test_err = np.zeros(epoch+1), np.zeros(epoch+1)
        # 予測（学習データ）
        y_train = predict(nx_train, W, b)
        # 予測（テストデータ）
        y_test = predict(nx_test, W, b)
        # 正解率、誤差表示
        train_rate[0], train_err[0] = accuracy_rate(y_train, t_train), cross_entropy_error(y_train, t_train)
        test_rate[0], test_err[0] = accuracy_rate(y_test, t_test), cross_entropy_error(y_test, t_test)
        print("{0:3d} 学習正解率={1:6.2f}% テスト正解率={2:6.2f}% 学習データ誤差={3:8.5f} テストデータ誤差={4:8.5f}".format(0, train_rate[0]*100, test_rate[0]*100, train_err[0], test_err[0]))

        # 開始時刻設定
        start_time = time.time()
        for i in range(epoch):
            # 学習
            for j in range(0, sx_train.shape[0], batch_size):
                W, b = learn(sx_train[j:j+batch_size], st_train[j:j+batch_size], W, b, lr)
            # 予測（学習データ）
            y_train = predict(nx_train, W, b)
            # 予測（テストデータ）
            y_test = predict(nx_test, W, b)
            # 正解率、誤差表示
            train_rate[i+1], train_err[i+1] = accuracy_rate(y_train, t_train), cross_entropy_error(y_train, t_train)
            test_rate[i+1], test_err[i+1] = accuracy_rate(y_test, t_test), cross_entropy_error(y_test, t_test)
            print("{0:3d} 学習正解率={1:6.2f}% テスト正解率={2:6.2f}% 学習データ誤差={3:8.5f} テストデータ誤差={4:8.5f}".format((i+1), train_rate[i+1]*100, test_rate[i+1]*100, train_err[i+1], test_err[i+1]))

        train_rates[name], train_errs[name] = train_rate, train_err
        test_rates[name],  test_errs[name]  = test_rate,  test_err
        # 終了時刻設定
        end_time = time.time()
        total_times[name] = end_time - start_time
        print("所要時間 = " + str(int(total_times[name]/60))  +" 分 " + str(int(total_times[name]%60)) + " 秒")

各実行でのテスト正解率の最高の値です。

W 1 W 2 W 3 W 4 W 5 W 6 W 7 W 8 W 9 W 10 平均
x 1 98.17 97.96 98.21 98.13 98.13 98.10 98.16 98.18 98.12 98.36 98.15
x 2 98.26 97.91 98.31 97.89 98.14 98.26 98.21 98.17 98.05 98.15 98.14
x 3 98.28 97.87 98.11 98.19 98.23 97.92 98.33 98.12 97.90 98.17 98.11
x 4 98.13 98.12 98.10 98.23 98.10 98.16 98.01 98.13 98.17 98.25 98.14
x 5 98.12 98.11 98.15 98.20 98.12 98.23 98.14 98.23 98.07 98.22 98.16
x 6 98.09 98.07 98.22 98.13 98.00 98.28 98.18 98.05 98.08 98.26 98.14
x 7 98.02 98.12 98.11 98.22 98.02 98.37 98.12 98.18 98.09 98.21 98.15
x 8 98.33 98.14 98.25 98.28 98.08 98.25 98.18 98.10 98.17 98.09 98.19
x 9 98.17 98.19 98.19 98.18 98.25 98.15 98.22 98.22 98.06 98.11 98.17
x 10 98.30 97.84 98.21 98.07 97.89 98.20 98.11 98.18 98.15 98.12 98.11
平均 98.19 98.03 98.19 98.15 98.10 98.19 98.17 98.16 98.09 98.19 98.14

グラフにしてみましょう。

import matplotlib.pyplot as plt
xWseed = np.zeros((11,11))
for m in range(10):
    for n in range(10):
        name = "xseed=" + str(m+1) + " Wseed=" + str(n+1)
        xWseed[m+1,n+1] = np.max(test_rates[name])
plt.imshow(xWseed, "bwr", vmin = 0.977, vmax = 0.983)
plt.colorbar()
plt.xlim(0.5,10.5)
plt.ylim(10.5,0.5)
plt.xticks(np.arange(1,11))
plt.yticks(np.arange(1,11))
plt.xlabel("W seed")
plt.ylabel("x seed")
plt.show()

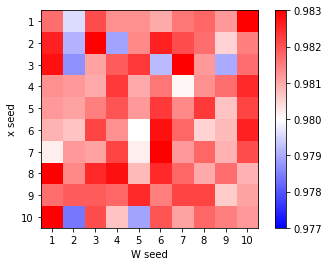
random_x_W.png

xはデータのシャッフルのseed値、Wは重みの初期値のseed値です。
結構大きな差がありますね。最高が98.37%、最低が97.84%です。0.5%も差があります。
平均を見てみると、データのシャッフルは98.1%台であまり変わりません。重みの初期値は、seed値が2と9の場合、少し悪いです。
ただ、何が良いseed値か判断する方法がわかりません。実行してみるしかないです。

参考までに、シャッフルなしでも実行してみました。重みの初期値のseed値を変更します。
テスト正解率の最大値です。

W 1 W 2 W 3 W 4 W 5 W 6 W 7 W 8 W 9 W 10
x 1 98.20 98.03 97.56 98.12 97.73 98.19 98.27 98.22 98.08 98.17

random_W.png

やはり、差がかなりありますね。
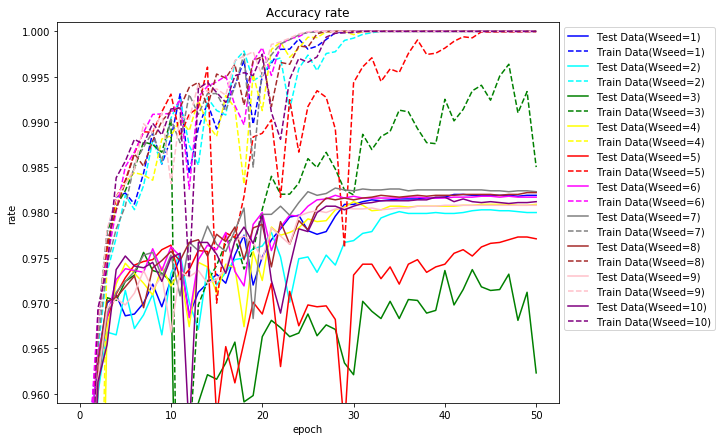
50エポックまでの正解率のグラフを描いてみます。

random_W_plot.png

以降、ハイパーパラメータを変更しながら実行します。1つの乱数のみで実行しますので、たまたま良い値になっている場合や悪い値になっている場合があると思われます。この前提でご覧ください。

※「ディープラーニングを実装から学ぶ～ (まとめ１）」について、単純化のため重みの初期値をHeの初期値から-0.1～0.1の乱数に変更しました。以降は、変更前のプログラムで実行しています。プログラムは、一番下の参考を参照してください。

中間層－なし

実行

まずは、中間層なしで試してみます。
ハイパーパラメータのうち、学習率、バッチサイズを変更して試してみます。

  • 学習率：1.0,0.5,0.1,0.05,0.01
  • バッチサイズ：1000,500,100,50,10,5

エポック数は、50固定としています。

import numpy as np
import time

train_rates = {}
test_rates = {}
total_times = {}

# MNISTデータ読み込み
x_train, t_train, x_test, t_test = load_mnist('c:\\mnist\\')

# 入力データの正規化
stats = {}
nx_train, train_stats = min_max(x_train, **stats)
nx_test,  test_stats  = min_max(x_test, **train_stats)

# 学習回数
epoch = 50
# ノード数
mds = [[]]
# 学習率
lrs = [1.0,0.5,0.1,0.05,0.01]
# バッチサイズ
batch_sizes = [1000,500,100,50,10,5]

for batch_size in batch_sizes:
    for lr in lrs:
        for md in mds:
            np.random.seed(8)
            train_rate = np.zeros(epoch+1)
            test_rate = np.zeros(epoch+1)
            d = [nx_train.shape[1]] + md + [10] 
            name = "lr=" + str(lr) + " d=" + str(d) + " batch_size=" + str(batch_size)
            print(name)

            # 重み、バイアスの初期化
            W = {}
            b = {}
            for i in range(1, len(d)):
                W[i] = he_normal(d[i-1], d[i])
                b[i] = np.zeros(d[i])

            # 予測（学習データ）
            y_train = predict(nx_train, W, b)
            train_rate[0] = accuracy_rate(y_train, t_train)
            # 予測（テストデータ）
            y_test = predict(nx_test, W, b)
            test_rate[0] = accuracy_rate(y_test, t_test)
            print("{0:3d} 学習正解率={1:6.2f}% テスト正解率={2:6.2f}%".format(0, train_rate[0]*100, test_rate[0]*100))

            # 開始時刻設定
            start_time = time.time()
            for i in range(epoch):
                # 学習
                for j in range(0, nx_train.shape[0], batch_size):
                    W, b = learn(nx_train[j:j+batch_size], t_train[j:j+batch_size], W, b, lr)
                # 予測（学習データ）
                y_train = predict(nx_train, W, b)
                train_rate[i+1] = accuracy_rate(y_train, t_train)
                # 予測（テストデータ）
                y_test = predict(nx_test, W, b)
                test_rate[i+1] = accuracy_rate(y_test, t_test)
                print("{0:3d} 学習正解率={1:6.2f}% テスト正解率={2:6.2f}%".format((i+1), train_rate[i+1]*100, test_rate[i+1]*100))

            train_rates[name] = train_rate
            test_rates[name] = test_rate
            # 終了時刻設定
            end_time = time.time()
            total_times[name] = end_time - start_time
            print("所要時間 = " + str(int(total_times[name]/60))  +" 分 " + str(int(total_times[name]%60)) + " 秒")

結果

各バッチサイズに対応するテストデータの正解率を示します。50エポック中の最高値です。括弧内は、正解率が最高となったエポック数です。
太字は、全体の最高を、斜字は、同一バッチサイズ中での最高を表します。
時間は、私のノートPC(Windows10、CPU:Core i3、メモリ:4GB)で実行した場合の所要時間です。

バッチサイズ 1.0 0.5 0.1 0.05 0.01 時間
1000 92.53(40) 92.44(50) 91.92(50) 91.50(49) 89.19(50) 1分41秒
500 92.32(47) 92.56(50) 92.27(48) 91.92(50) 90.35(50) 1分40秒
100 91.31(25) 91.79(34) 92.51(41) 92.48(50) 91.92(50) 0分55秒
50 90.19(16) 91.47(45) 92.37(47) 92.53(48) 92.27(49) 0分58秒
10 88.43(18) 87.85( 2) 91.45(31) 92.01(18) 92.56(50) 1分36秒
5 89.09( 6) 88.26( 6) 90.35(12) 91.42(46) 92.38(39) 2分 5秒

dm=[].png

中間層なしでも92.5%程度の正解率になりました。
バッチサイズが大きいほど学習率が大きい方が良いようです。表にはありませんが、バッチサイズ5の時、学習率を0.005とすると正解率が92.56となり最高タイとなりました。
バッチサイズに応じて学習率を設定する必要がありそうです。

中間層数－１

実行

ハイパーパラメータのうち、層数、ノート数、学習率、バッチサイズを変更して試してみます。
まずは、中間層の数を１として、以下変更しながら実行します。

  • ノード数：[1],[5],[10],[50],[100],[500]
  • 学習率：1.0,0.5,0.1,0.05,0.01
  • バッチサイズ：1000,500,100,50,10,5

本当は、ノード数をもっと増やしたかったのですが、私の非力なノートPCだとリソース不足で断念しました。
ノード数のみ変更します。エポック数は、前と同じく50固定としています。

# ノード数
mds=[[1],[5],[10],[50],[100],[500]]

結果

ノード数

ノード数を変更した場合のテスト正解率です。50エポック中の最高値です。括弧内は、正解率が最高となったエポック数です。

バッチサイズが、100と10の場合の結果を表に示します。

  • バッチサイズ - 100
ノード数 1.0 0.5 0.1 0.05 0.01 時間
[1] 10.28( 1) 10.28( 1) 37.69(46) 35.64(34) 32.01(42) 0分46秒
[5] 12.68( 0) 54.51( 2) 88.62(10) 89.41(45) 89.68(50) 0分57秒
[10] 26.87(38) 91.82(46) 93.56(35) 93.89(50) 92.73(50) 1分 2秒
[50] 94.99(47) 97.38(49) 97.47(27) 97.38(49) 95.91(50) 1分51秒
[100] 97.25(49) 98.02(48) 97.78(50) 97.61(50) 96.26(50) 2分46秒
[500] 98.41(46) 98.34(47) 98.16(50) 97.98(49) 96.65(49) 14分19秒

dm=[x],batch_size=100.png

  • バッチサイズ - 10
ノード数 1.0 0.5 0.1 0.05 0.01 時間
[1] 9.58( 1) 9.58( 1) 34.64(50) 36.14(12) 38.39(50) 1分35秒
[5] 12.68( 0) 12.68( 0) 87.43(13) 88.20(30) 89.08(49) 1分40秒
[10] 17.48( 3) 27.13( 1) 92.04(18) 93.88(40) 93.86(44) 2分 6秒
[50] 22.91(13) 94.20(50) 97.29(45) 97.48(35) 97.41(48) 3分33秒
[100] 20.63( 3) 95.69(50) 98.17(33) 97.93(48) 97.76(47) 5分46秒
[500] 42.26( 3) 96.72(34) 98.49(29) 98.34(39) 98.13(50) 63分 4秒

dm=[x],batch_size=10.png

あたりまえですが、ノード数が多いほど、正解率は高くなりました。

バッチサイズ

ノード数が10,100の場合の結果を表にします。

  • ノード数 - [10]
バッチサイズ 1.0 0.5 0.1 0.05 0.01 時間
1000 28.79(17) 93.05(50) 92.73(50) 91.98(49) 89.56(50) 1分45秒
500 51.38( 2) 93.50(44) 93.09(43) 92.75(50) 90.89(50) 1分44秒
100 26.87(38) 91.82(46) 93.56(35) 93.89(50) 92.73(50) 1分 2秒
50 24.67(18) 90.90(19) 93.61(50) 93.51(28) 93.10(48) 1分 8秒
10 17.48( 3) 27.13( 1) 92.04(18) 93.88(40) 93.86(44) 2分 6秒
5 15.37( 1) 17.64( 1) 91.59(48) 92.27(40) 93.67(38) 2分52秒

dm=[10],batch_size=x.png

  • ノード数 - [100]
バッチサイズ 1.0 0.5 0.1 0.05 0.01 時間
1000 97.65(42) 97.70(50) 96.26(50) 94.84(50) 91.45(49) 3分 4秒
500 97.54(46) 97.80(46) 97.04(50) 96.27(50) 92.84(50) 3分 7秒
100 97.25(49) 98.02(48) 97.78(50) 97.61(50) 96.26(50) 2分46秒
50 96.60(50) 97.98(30) 97.86(42) 97.76(49) 97.09(47) 3分 9秒
10 20.63( 3) 95.69(50) 98.17(33) 97.93(48) 97.76(47) 5分46秒
5 10.99( 0) 59.71( 9) 97.70(36) 98.02(26) 97.91(50) 9分11秒

dm=[100],batch_size=x.png

バッチサイズは、10～100程度が良いようです。

学習率

ノード数やバッチサイズによって最適な学習率が変わってくるようです。

判明したこと

  • ノード数は多いほど正解率は高くなる。（500ノードまでの検証結果）
  • バッチサイズは、10～100程度がよさそう。
  • バッチサイズを小さくすると非常に時間がかかる。（500ノード、バッチサイズ100だと50エポックで約14分だが、バッチサイズ5だと約2時間）
  • 学習率は、ノード数やバッチサイズにより最適な値が異なる。
  • バッチサイズが小さいほど、学習率も小さくするとよさそう。
  • ノード数が小さいほど、学習率も小さくするとよさそう。

ノード数、バッチサイズ、学習率は互いに関係があり、また、マシンリソースの消費や実行時間も含めて考える必要があり、最適な値を見つけることはなかなか大変です。

中間層数－２

実行

中間層を２層とし実行します。
ノード数を10,50,100の組み合わせで試してみます。

  • ノード数：[10,10],[10,50],[10,100],[50,10],[50,50],[50,100],[100,10],[100,50],[100,100]
  • 学習率：1.0,0.5,0.1,0.05,0.01
  • バッチサイズ：1000,500,100,50,10,5

ノード数の部分を変更します。

# ノード数
mds=[[10,10],[10,50],[10,100],[50,10],[50,50],[50,100],[100,10],[100,50],[100,100]]

結果

ノード数

バッチサイズが、100と10の場合の結果を表に示します。

  • バッチサイズ - 100
ノード数 1.0 0.5 0.1 0.05 0.01 時間
[10, 10] 15.29( 0) 90.83(50) 93.43(50) 93.40(23) 93.29(50) 1分 9秒
[10, 50] 14.31( 0) 90.24(27) 95.00(49) 95.18(41) 94.51(50) 1分27秒
[10, 100] 11.76( 1) 29.06(44) 95.17(45) 95.33(48) 94.77(50) 1分48秒
[50, 10] 95.22(40) 96.34(35) 97.06(25) 96.82(50) 96.65(47) 1分57秒
[50, 50] 47.90( 2) 97.04(17) 97.19(44) 96.97(43) 96.71(50) 2分16秒
[50, 100] 27.09(33) 97.70(44) 97.71(50) 97.53(25) 96.89(50) 2分39秒
[100, 10] 10.28( 1) 97.65(39) 97.77(41) 97.64(28) 96.82(48) 2分52秒
[100, 50] 96.59(15) 97.89(49) 98.01(43) 97.92(49) 97.08(50) 3分13秒
[100, 100] 95.86(50) 98.21(30) 97.80(40) 97.64(50) 97.07(49) 3分37秒

dm=[x,y],batch_size=100.png

  • バッチサイズ - 10
ノード数 1.0 0.5 0.1 0.05 0.01 時間
[10, 10] 15.29( 0) 15.29( 0) 92.35(49) 92.70(21) 93.45(50) 2分29秒
[10, 50] 14.31( 0) 14.31( 0) 92.91(27) 94.67(19) 95.47(34) 2分47秒
[10, 100] 10.02( 0) 10.02( 0) 94.03(22) 93.98(14) 95.42(47) 3分 6秒
[50, 10] 9.58( 1) 31.88( 1) 96.92(32) 96.93(50) 96.95(50) 3分57秒
[50, 50] 12.42( 6) 29.02( 2) 97.24(40) 97.51(38) 97.12(49) 4分20秒
[50, 100] 9.58( 1) 9.58( 1) 97.28(28) 97.51(41) 97.49(49) 4分51秒
[100, 10] 9.58( 1) 9.58( 1) 97.65(40) 97.73(37) 97.74(46) 6分19秒
[100, 50] 9.58( 1) 69.53( 1) 97.75(30) 98.11(29) 97.96(44) 7分 1秒
[100, 100] 10.43( 0) 69.23( 1) 97.73(43) 98.21(42) 97.76(47) 7分46秒

dm=[x,y],batch_size=10.png

ノード数が大きければ大きいほど良い結果になりましたが、１層目が小さいと良い結果になりません。

バッチサイズ

ノード数が[50,100],[100,50]の場合の結果を表にします。

  • ノード数 - [50,100]
バッチサイズ 1.0 0.5 0.1 0.05 0.01 時間
1000 85.19(18) 96.82(30) 96.86(49) 96.12(50) 92.79(50) 3分 3秒
500 93.40(46) 97.33(20) 97.32(49) 96.89(50) 94.44(50) 3分 4秒
100 27.09(33) 97.70(44) 97.71(50) 97.53(25) 96.89(50) 2分39秒
50 9.58( 1) 96.49(31) 97.39(50) 97.55(50) 97.40(50) 2分49秒
10 9.58( 1) 9.58( 1) 97.28(28) 97.51(41) 97.49(49) 4分51秒
5 9.58( 1) 9.58( 1) 96.31(18) 97.06(21) 97.74(49) 8分58秒

dm=[50,100],batch_size=x.png

  • ノード数 - [100,50]
バッチサイズ 1.0 0.5 0.1 0.05 0.01 時間
1000 96.26(24) 97.51(24) 97.15(49) 96.03(50) 92.46(50) 3分27秒
500 10.28( 1) 97.79(44) 97.73(50) 97.06(50) 94.12(50) 3分31秒
100 96.59(15) 97.89(49) 98.01(43) 97.92(49) 97.08(50) 3分13秒
50 94.46(15) 97.41(50) 98.09(41) 98.09(36) 97.63(50) 3分40秒
10 9.58( 1) 69.53( 1) 97.75(30) 98.11(29) 97.96(44) 7分 1秒
5 9.58( 1) 18.54( 9) 97.25(34) 97.76(49) 98.03(46) 11分11秒

dm=[100,50],batch_size=x.png

学習率

バッチサイズ、ノード数が小さいほど、学習率も小さくするとよさそうです。

判明したこと

  • 中間層の１層目のノード数を小さくすると正解率が良くない。層の順にノード数を小さくしていくのが良さそうである。
  • 中間層１層よりは、良い結果となったが、２層にしたからと言って大きく正解率が向上するわけではない。

中間層数－多階層

実行

ノード数を100とし中間層を増やしながら実行します。

  • ノード数：[100],[100,100],[100,100,100],[100,100,100,100],[100,100,100,100,100],[100,100,100,100,100,100]
  • 学習率：1.0,0.5,0.1,0.05,0.01
  • バッチサイズ：1000,500,100,50,10,5

ノード数の部分を変更します。

# ノード数
mds=[[100],[100,100],[100,100,100],[100,100,100,100],[100,100,100,100,100],[100,100,100,100,100,100]]

結果

ノード数

バッチサイズが、100と10の場合の結果を表に示します。

  • バッチサイズ - 100
ノード数 1.0 0.5 0.1 0.05 0.01 時間
[100] 97.25(49) 98.02(48) 97.78(50) 97.61(50) 96.26(50) 2分46秒
[100, 100] 95.86(50) 98.21(30) 97.80(40) 97.64(50) 97.07(49) 3分37秒
[100, 100, 100] 10.28( 1) 97.85(24) 97.80(40) 97.85(41) 97.40(50) 4分31秒
[100, 100, 100, 100] 9.80( 1) 97.95(43) 97.75(30) 97.76(49) 97.09(46) 5分21秒
[100, 100, 100, 100, 100] 11.57( 0) 11.57( 0) 97.90(49) 97.67(44) 97.36(50) 6分13秒
[100, 100, 100, 100, 100, 100] 10.28( 2) 9.98( 0) 98.07(43) 97.90(45) 97.12(45) 7分 8秒

dm=[x,y,...],batch_size=100.png

  • バッチサイズ - 10
ノード数 1.0 0.5 0.1 0.05 0.01 時間
[100] 20.63( 3) 95.69(50) 98.17(33) 97.93(48) 97.76(47) 5分46秒
[100, 100] 10.43( 0) 69.23( 1) 97.73(43) 98.21(42) 97.76(47) 7分46秒
[100, 100, 100] 9.58( 1) 27.39( 1) 97.92(32) 98.23(36) 97.89(44) 9分18秒
[100, 100, 100, 100] 9.80( 1) 9.58( 1) 98.13(49) 98.23(42) 97.96(46) 11分10秒
[100, 100, 100, 100, 100] 11.57( 0) 11.57( 0) 97.89(40) 98.09(38) 98.14(41) 12分48秒
[100, 100, 100, 100, 100, 100] 9.98( 0) 9.98( 0) 97.87(50) 98.07(37) 98.15(49) 14分15秒

dm=[x,y,...],batch_size=10.png

階層数を大きくすればするほど良いというわけではありませんでした。

バッチサイズ

ノード数が[100, 100, 100],[100, 100, 100, 100, 100, 100]の場合の結果を表にします。

  • ノード数 - [100, 100, 100]
バッチサイズ 1.0 0.5 0.1 0.05 0.01 時間
1000 95.24(29) 96.99(16) 97.47(49) 96.74(50) 93.75(50) 4分36秒
500 96.53(30) 97.24(11) 97.68(45) 97.34(50) 95.11(50) 4分42秒
100 10.28( 1) 97.85(24) 97.80(40) 97.85(41) 97.40(50) 4分31秒
50 9.80( 1) 97.81(47) 98.11(37) 97.92(31) 97.46(44) 5分 8秒
10 9.58( 1) 27.39( 1) 97.92(32) 98.23(36) 97.89(44) 9分18秒
5 9.58( 1) 9.58( 1) 96.87(13) 97.75(30) 98.13(34) 15分10秒

dm=[100,100,100],batch_size=x.png

  • ノード数 - [100, 100, 100, 100, 100, 100]
バッチサイズ 1.0 0.5 0.1 0.05 0.01 時間
1000 9.98( 0) 96.28(21) 97.17(29) 96.96(47) 95.20(50) 7分 0秒
500 9.98( 0) 96.81(14) 97.62(39) 97.27(49) 96.40(50) 7分 6秒
100 10.28( 2) 9.98( 0) 98.07(43) 97.90(45) 97.12(45) 7分 8秒
50 9.98( 0) 96.76(18) 98.10(50) 98.03(46) 97.41(39) 7分52秒
10 9.98( 0) 9.98( 0) 97.87(50) 98.07(37) 98.15(49) 14分15秒
5 9.98( 0) 9.98( 0) 96.55( 8) 98.01(46) 97.86(36) 23分12秒

dm=[100,100,100,100,100,100],batch_size=x.png

判明したこと

  • 階層数を深くすればするほど良いわけではない。

エポック

今までは、エポック数を50で固定していました。
中間層のノード数を[100,50]の場合で、学習率を0.5,0.1,0.05として、1000エポックまで実行してみました。バッチサイズは、100です。
エポック数、50,100,1000の場合のテストデータの最高正解率と最高正解率となったエポック数です。

実行エポック数 0.5 0.1 0.05
50 97.89(49) 98.01(43) 97.92(49)
100 98.00(76) 98.04(59) 97.99(76)
1000 98.04(486) 98.12(337) 97.99(76)

それぞれエポック数を増やせばテストデータに対する正解率が少し向上することがわかりました。エポック数は、どこまで実行すればよいのか、グラフで確認してみます。
100エポックまでの誤差と正解率のグラフです。

  • 学習率 - 0.5

Error_dm=[100,50],lr=0.5.png

Accuracy_rate_dm=[100,50],lr=0.5.png

40エポック程度で、学習データに対する誤差は、ほぼ0になりました。テストデータに対する誤差は、40エポック以降は微増になっています。学習データの正解率も40エポックでほぼ100%になりました。ただ、テストデータに対する正解率も微増しています。

  • 学習率 - 0.1

Error_dm=[100,50],lr=0.1.png

Accuracy_rate_dm=[100,50],lr=0.1.png

学習率0.5のグラフと比べて序盤は滑らかになりました。50エポック程度で学習データに対する誤差がほぼ0となり、正解率は、ほぼ100%になりました。

  • 学習率 - 0.05

Error_dm=[100,50],lr=0.05.png

Accuracy_rate_dm=[100,50],lr=0.05.png

かなり滑らかなグラフになりましたが、誤差の減少や正解率の向上度合いが今までに比べて遅くなっています。

途中からテストデータに対する誤差が増加していきます。この状態を過学習と言います。学習データにはフィットするが、未学習のデータに対して精度が悪くなる状態です。MNISTでは、誤差が増えても正解率は悪くなりませんでしたが、一般的には、誤差が増えると正解率も下がるものと思われます。
誤差が数回連続で上昇したら学習を打ち切るのがよいとされています。
テストデータの誤差のグラフを書いてみます。誤差が減少した場合は、青▼、増加した場合は、赤▲で示します。

  • 学習率 - 0.5

ErrorUD_dm=[100,50],lr=0.5.png

  • 学習率 - 0.1

ErrorUD_dm=[100,50],lr=0.1.png

  • 学習率 - 0.05

ErrorUD_dm=[100,50],lr=0.05.png

テストデータの誤差が連続して増加した場合、学習を打ち切るとした場合の正解率です。

増加回数 0.5 0.1 0.05
2回連続増加 97.12(9) 97.50(12) 97.73(26)
3回連続増加 97.12(9) 97.89(21) 97.82(29)
4回連続増加 97.81(40) 97.89(21) 97.82(29)
5回連続増加 97.81(40) 97.89(21) 97.82(29)
10回連続増加 97.81(40) 98.00(42) 97.89(37)
(参考)50 97.89(49) 98.01(43) 97.92(49)
(参考)100 98.00(76) 98.04(59) 97.99(76)
(参考)1000 98.04(486) 98.12(337) 97.99(76)

どこで打ち切るかの判断は非常に難しいですね。

テストデータの誤差で打ち切りを判断した場合は、テストデータに対しても学習することとなり、学習データ、テストデータの他に検証データを準備し、打ち切りが正しいか判断する必要があるようです。MNISTの場合は、学習データの一部を検証データとして学習には利用しないデータとして切り出しておく必要があります。

判明したこと

  • 学習データの誤差がほぼ0になると学習が進まなくなる。この時点で過学習となっている可能性がある。
  • 学習の打ち切りは、誤差が連続して増加した場合が良いようであるが、判断は難しい。

まとめ

階層数、ノード数、バッチサイズ、学習率を変更しながら試してみました。
各ハイパーパラメータ間には関連があり、例えば、適切なバッチサイズや学習率を定めたとしても、ノード数を変更すれば、定めた値も適切ではなくなります。また、値を少し変えるだけで結果も大きく変わり、非常に繊細です。
また、学習をどこで打ち切るかも難しいです。

  • ハイパーパラメータは、相互に依存しており、最適な値は試して確認するしかない。
  • 学習をどこで打ち切るかも、最適なエポック数を定めることは困難である。

次は、学習中に何か起きているか見てみることにします。

参考

今回変更したプログラム全体です。誤差も取得するようにしています。

  • 関数
import numpy as np
# affine変換
def affine(z, W, b):
    return np.dot(z, W) + b
# affine変換勾配
def affine_back(du, z, W, b):
    dz = np.dot(du, W.T)
    dW = np.dot(z.T, du)
    db = np.dot(np.ones(z.shape[0]).T, du)
    return dz, dW, db
# 活性化関数(ReLU)
def relu(u):
    return np.maximum(0, u)
# 活性化関数(ReLU)勾配
def relu_back(dz, u):
    return dz * np.where(u > 0, 1, 0)
# 活性化関数(softmax)
def softmax(u):
    max_u = np.max(u, axis=1, keepdims=True)
    exp_u = np.exp(u-max_u)
    return exp_u/np.sum(exp_u, axis=1, keepdims=True)
# 誤差(交差エントロピー）
def cross_entropy_error(y, t):
    return -np.sum(t * np.log(np.maximum(y,1e-7)))/y.shape[0]
# 誤差(交差エントロピー）＋活性化関数(softmax)勾配
def softmax_cross_entropy_error_back(y, t):
    return (y - t)/y.shape[0]
  • 学習・予測

学習

def learn(x, t, W, b, lr):
    # 層数
    layer = len(W)
    # 順伝播
    u = {}
    z = {}
    z[0] = x
    for i in range(1, layer):
        u[i] = affine(z[i-1], W[i], b[i])
        z[i] = relu(u[i])
    u[layer] = affine(z[layer-1], W[layer], b[layer])
    y  = softmax(u[layer])
    # 逆伝播
    dz = {}
    du = {}
    dW = {}
    db = {}
    du[layer] = softmax_cross_entropy_error_back(y, t)
    dz[layer-1], dW[layer], db[layer] = affine_back(du[layer], z[layer-1], W[layer], b[layer])
    for i in range(layer-1, 0, -1):
        du[i] = relu_back(dz[i], u[i])
        dz[i-1], dW[i], db[i] = affine_back(du[i], z[i-1], W[i], b[i])
    # 重み、バイアスの更新
    for i in range(1, layer+1):
        W[i] = W[i] - lr * dW[i]
        b[i] = b[i] - lr * db[i]
    return W, b

予測

def predict(x, W, b):
    # 層数
    layer = len(W) 
    # 順伝播
    u = {}
    z = {}
    z[0] = x
    for i in range(1, layer):
        u[i] = affine(z[i-1], W[i], b[i])
        z[i] = relu(u[i])
    u[layer] = affine(z[layer-1], W[layer], b[layer])
    y  = softmax(u[layer])
    return y
  • 実行
import gzip
import numpy as np
# MNIST読み込み
def load_mnist( mnist_path ) :
    return _load_image(mnist_path + 'train-images-idx3-ubyte.gz'), \
           _load_label(mnist_path + 'train-labels-idx1-ubyte.gz'), \
           _load_image(mnist_path + 't10k-images-idx3-ubyte.gz'), \
           _load_label(mnist_path + 't10k-labels-idx1-ubyte.gz')
def _load_image( image_path ) :
    # 画像データの読み込み
    with gzip.open(image_path, 'rb') as f:
        buffer = f.read()
    size = np.frombuffer(buffer, np.dtype('>i4'), 1, offset=4)
    rows = np.frombuffer(buffer, np.dtype('>i4'), 1, offset=8)
    columns = np.frombuffer(buffer, np.dtype('>i4'), 1, offset=12)
    data = np.frombuffer(buffer, np.uint8, offset=16)
    image = np.reshape(data, (size[0], rows[0]*columns[0]))
    image = image.astype(np.float32)
    return image
def _load_label( label_path ) :
    # 正解データ読み込み
    with gzip.open(label_path, 'rb') as f:
        buffer = f.read()
    size = np.frombuffer(buffer, np.dtype('>i4'), 1, offset=4)
    data = np.frombuffer(buffer, np.uint8, offset=8)
    label = np.zeros((size[0], 10))
    for i in range(size[0]):
        label[i, data[i]] = 1
    return label

# 正規化関数
def min_max(x, min=None, max=None, axis=None):
    if min is None:
        min = np.min(x, axis=axis, keepdims=True) # 最小値を求める
    if max is None:
        max = np.max(x, axis=axis, keepdims=True) # 最大値を求める
    return (x-min)/np.maximum((max-min),1e-7), {"min":min, "max":max}

# 重み初期化関数
def he_normal(d_1, d):
    var = np.sqrt(2/d_1)
    return np.random.normal(0, var, (d_1, d))

# 正解率
def accuracy_rate(y, t):
    max_y = np.argmax(y, axis=1)
    max_t = np.argmax(t, axis=1)
    return np.sum(max_y == max_t)/y.shape[0]

import numpy as np
import time

train_rates = {}
test_rates = {}
train_errs = {}
test_errs = {}
total_times = {}

# MNISTデータ読み込み
x_train, t_train, x_test, t_test = load_mnist('c:\\mnist\\')

# 入力データの正規化
stats = {}
nx_train, train_stats = min_max(x_train, **stats)
nx_test,  test_stats  = min_max(x_test, **train_stats)

# 学習回数
epoch = 50
# ノード数
mds = [[100,50]]
# 学習率
lrs = [1.0,0.5,0.1,0.05,0.01]
# バッチサイズ
batch_sizes = [1000,500,100,50,10,5]

for batch_size in batch_sizes:
    for lr in lrs:
        for md in mds:
            np.random.seed(8)
            train_rate = np.zeros(epoch+1)
            test_rate = np.zeros(epoch+1)
            train_err = np.zeros(epoch+1)
            test_err = np.zeros(epoch+1)
            d = [nx_train.shape[1]] + md + [10] 
            name = "lr=" + str(lr) + " d=" + str(d) + " batch_size=" + str(batch_size)
            print(name)

            # 重み、バイアスの初期化
            W = {}
            b = {}
            for i in range(1, len(d)):
                W[i] = he_normal(d[i-1], d[i])
                b[i] = np.zeros(d[i])

            # 予測（学習データ）
            y_train = predict(nx_train, W, b)
            train_rate[0] = accuracy_rate(y_train, t_train)
            train_err[0] = cross_entropy_error(y_train, t_train)
            # 予測（テストデータ）
            y_test = predict(nx_test, W, b)
            test_rate[0] = accuracy_rate(y_test, t_test)
            test_err[0] = cross_entropy_error(y_test, t_test)
            print("{0:3d} 学習正解率={1:6.2f}% テスト正解率={2:6.2f}% 学習データ誤差={3:8.4f} テストデータ誤差={4:8.4f}".format(0, train_rate[0]*100, test_rate[0]*100, train_err[0], test_err[0]))

            # 開始時刻設定
            start_time = time.time()
            for i in range(epoch):
                # 学習
                for j in range(0, nx_train.shape[0], batch_size):
                    W, b = learn(nx_train[j:j+batch_size], t_train[j:j+batch_size], W, b, lr)
                # 予測（学習データ）
                y_train = predict(nx_train, W, b)
                train_rate[i+1] = accuracy_rate(y_train, t_train)
                train_err[i+1] = cross_entropy_error(y_train, t_train)
                # 予測（テストデータ）
                y_test = predict(nx_test, W, b)
                test_rate[i+1] = accuracy_rate(y_test, t_test)
                test_err[i+1] = cross_entropy_error(y_test, t_test)
                print("{0:3d} 学習正解率={1:6.2f}% テスト正解率={2:6.2f}% 学習データ誤差={3:8.4f} テストデータ誤差={4:8.4f}".format((i+1), train_rate[i+1]*100, test_rate[i+1]*100, train_err[i+1], test_err[i+1]))

            train_rates[name] = train_rate
            test_rates[name] = test_rate
            train_errs[name] = train_err
            test_errs[name] = test_err
            # 終了時刻設定
            end_time = time.time()
            total_times[name] = end_time - start_time
            print("所要時間 = " + str(int(total_times[name]/60))  +" 分 " + str(int(total_times[name]%60)) + " 秒")

以下の部分を適宜変更して実行してください。

# 学習回数
epoch = 50
# ノード数
mds = [[100,50]]
# 学習率
lrs = [1.0,0.5,0.1,0.05,0.01]
# バッチサイズ
batch_sizes = [1000,500,100,50,10,5]

改版履歴
2018/6/23 乱数の影響を追加

9
12
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
9
12