MNISTの予測をディープラーニング(ニューラルネットワーク)で行います。実は、ディープラーニング(ニューラルネットワーク)の実装は簡単です。数十ステップで98%程度の精度を達成できます。
(注意事項)
ディープラーニング(ニューラルネットワーク)の学習方法を理解すること目的としたプログラムです。MNISTデータ程度のデータを想定しています。大量のデータやデータによっては、この実装だけは対応できません。。あくまでもディープラーニング(ニューラルネットワーク)の基本を理解するという視点でご覧ください。
ニューラルネットワーク
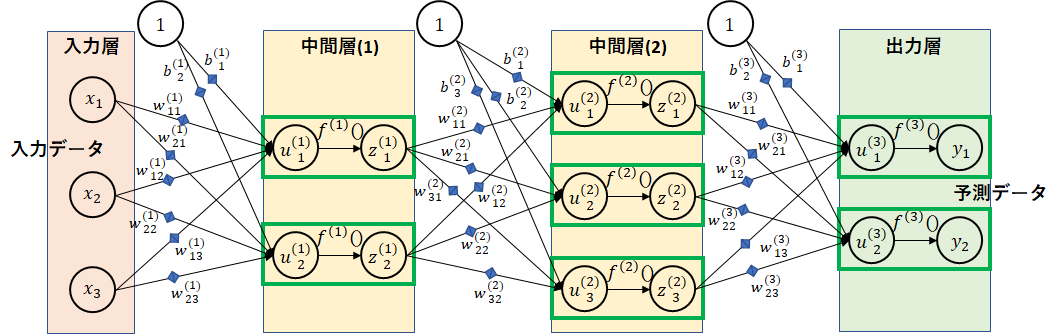
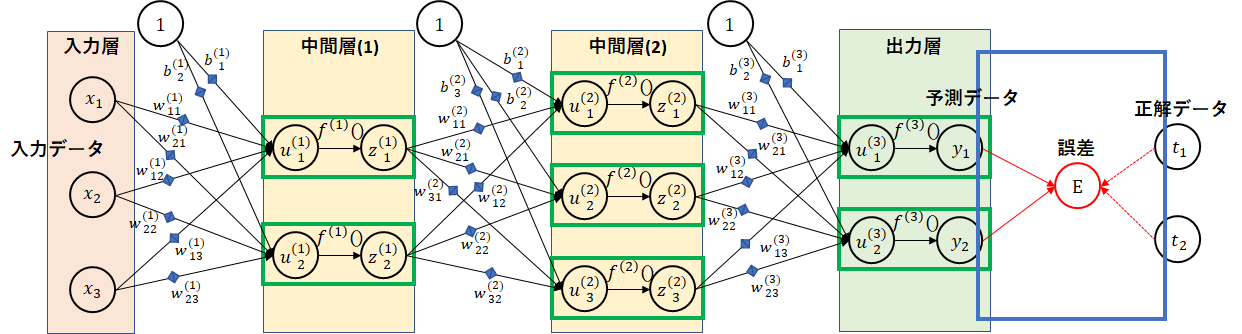
以下のような図を見たことがありますか?脳を模倣したニューラルネットワークです。
緑枠が脳細胞を表すニューロンです。ニューロンとニューロンの間はシナプス(青の◆)で結合しています。シナプスでのデータの受け渡し度合いを重み($ w $)で表します。ニューロン間の結合の度合い、太さとも言えます。
図の関係で、中間層の階層数は2階層としています。この階層数をいくらでも深くできることからディープラーニング(深層学習)と言われます。また、各層のノード数(ニューロンの数)も図では2~3個にしていますが、実際にはもっと多くのノード数となります。
学習
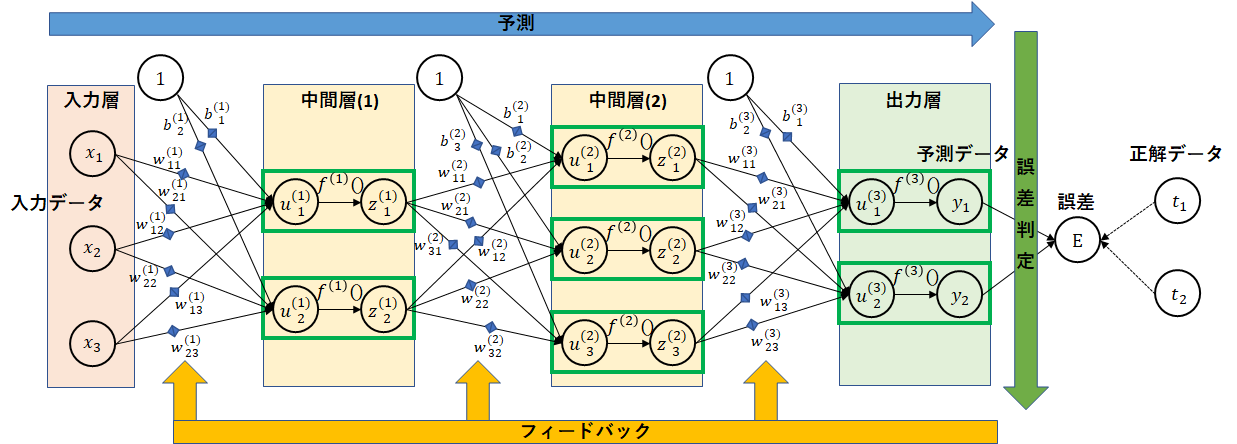
ニューラルネットワークを通して学習を行います。学習は、正解データを持ったデータで行います。
入力層から入ったデータをもとに各層を通じて予測データを求めます。次に、正解データとの誤差を計算します。最後に、誤差をもとに誤差がより小さくなるように重みの調整を行います。
実装
実装は、pythonで行います。行列演算、数値計算を行うことが可能なnumpyを用います。
affine変換
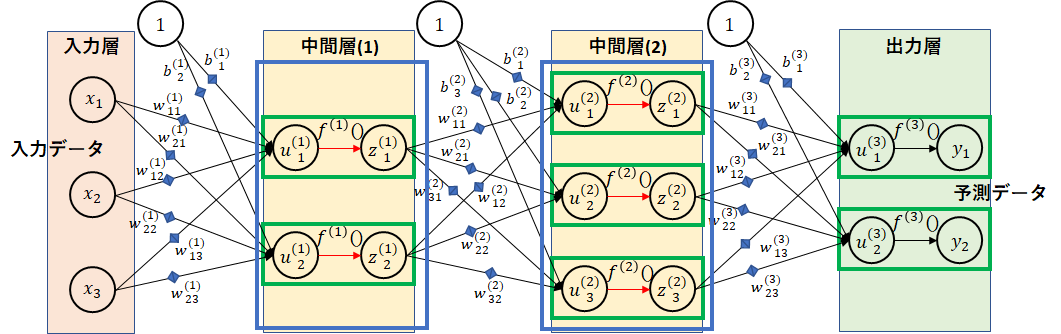
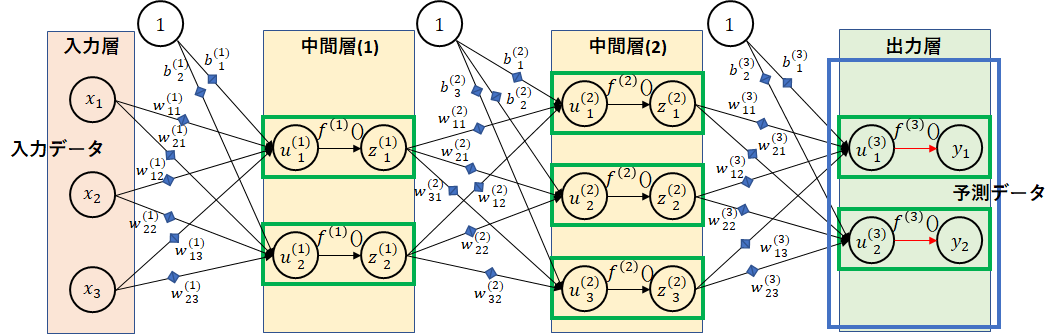
シナプスによる結合部分の計算になります。図で青枠の部分です。
$ u_1^{(1)} $の計算は、以下の式で表せます。
u_1^{(1)} = w_{11}^{(1)}x_1 + w_{12}^{(1)}x_2 + w_{13}^{(1)}x_3 + b_1^{(1)}
入力層と中間層(1)の間を行列で表すと以下になります。
\begin{pmatrix}
u_1^{(1)}\\
u_2^{(1)}
\end{pmatrix}
=
\begin{pmatrix}
w_{11}^{(1)} & w_{12}^{(1)} & w_{13}^{(1)}\\
w_{21}^{(1)} & w_{22}^{(1)} & w_{23}^{(1)}
\end{pmatrix}
\begin{pmatrix}
x_1\\
x_2\\
x_3
\end{pmatrix}
+
\begin{pmatrix}
b_1^{(1)}\\
b_2^{(1)}
\end{pmatrix}
行列の内積(ドット積)で表せます。numpyでの実装は以下になります。
def affine(z, W, b):
return np.dot(z, W) + b
活性化関数(中間層)
活性化関数は、ニューロン内での発火を表します。図の青枠の部分です。
最近は、活性化関数としてReLUが用いられることが多いようです。
ReLUは、以下の関数です。入力が負になれば以降に情報は伝えません。正の場合は、そのままの値を伝えます。
f_{ReLU}(u) =
\left\{
\begin{array}{ll}
u & (u \gt 0) \\
0 & (u \le 0)
\end{array}
\right.
ReLUのグラフです。単純です。
実装は、以下になります。
def relu(u):
return np.maximum(0, u)
活性化関数(出力層)
MNISTのように0~9の数値に分類する分類問題の場合は、出力層の活性化関数としてsoftmax関数が利用されます。これは、各分類ごとの確率を求めるためです。総和は、1になります。
softmaxの式です。
f(u_i) = \frac{\exp(u_i)}{\sum_{k=1}^{n}\exp(u_k)}
実装は、以下になります。
def softmax(u):
max_u = np.max(u, axis=1, keepdims=True)
exp_u = np.exp(u-max_u)
return exp_u/np.sum(exp_u, axis=1, keepdims=True)
誤差関数
予測データと正解データの比較に誤差関数を用います。分類問題の場合は、交差エントロピー誤差を利用します。
交差エントロピー誤差の式です。
E= -\sum_kt_k\log{y_k}
実装は以下です。
def cross_entropy_error(y, t):
return -np.sum(t * np.log(np.maximum(y,1e-7)))/y.shape[0]
1e-7は、0のlogを取らないようにするための定数です。
重みの調整
誤差を小さくするように重みを調整します。
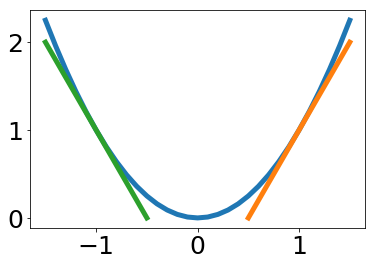
調整には、微分を利用します。誤差関数に対して微分することで傾き(勾配)を求めます。青の線を誤差関数とします。下の図のように、オレンジの場合は、勾配は正となり、値を小さくすることで誤差を小さくできます。逆に緑のように勾配が負となった場合は、値を大きくすることで誤差を小さくできます。
微分値(勾配)が、正となった場合は、重みを小さくするように調整します。負となった場合は、重みを大きくするように調整します。
最終的に、誤差Eに対する重みの微分を求めます。正式には偏微分を用います。
細かい説明は省略しますが、合成微分を用いて各重みの偏微分は以下のように表せます。
\begin{align}
\frac{\partial E}{\partial w^{(3)}} &=
\frac{\partial E}{\partial y}
\frac{\partial y}{\partial u^{(3)}}
\frac{\partial u^{(3)}}{\partial w^{(3)}}
\\
\frac{\partial E}{\partial w^{(2)}} &=
\frac{\partial E}{\partial y}
\frac{\partial y}{\partial u^{(3)}}
\frac{\partial u^{(3)}}{\partial z^{(2)}}
\frac{\partial z^{(2)}}{\partial u^{(2)}}
\frac{\partial u^{(2)}}{\partial w^{(2)}}
\\
\frac{\partial E}{\partial w^{(1)}} &=
\frac{\partial E}{\partial y}
\frac{\partial y}{\partial u^{(3)}}
\frac{\partial u^{(3)}}{\partial z^{(2)}}
\frac{\partial z^{(2)}}{\partial u^{(2)}}
\frac{\partial u^{(2)}}{\partial z^{(1)}}
\frac{\partial z^{(1)}}{\partial u^{(1)}}
\frac{\partial u^{(1)}}{\partial w^{(1)}}
\end{align}
難しそうに見えますが、逆から順番に微分値を掛けていくだけです。
各層の勾配を見ていきましょう。
誤差関数、活性化関数(出力層)の勾配
交差エントロピー誤差およびsoftmax関数の式は、以下でした。
E= -\sum_kt_k\log{y_k}
f(u_i) = \frac{\exp(u_i)}{\sum_{k=1}^{n}\exp(u_k)}
交差エントロピー+softmaxの勾配は、以下で表せます。
\frac{\partial E}{\partial u_i^{(3)}} = y_i - t_i
ここでは、微分を求めることが目的ではありませんので、詳細は省略します。詳しく知りたい方は、以下に書いておりますので参照してみてください。
ディープラーニングを実装から学ぶ(4-2)学習(誤差逆伝播法2)
実装は、以下となります。
def softmax_cross_entropy_error_back(y, t):
return (y - t)/y.shape[0]
複数データを同時に処理することを想定していますので、1データ当たりとするよう調整を入れています。
活性化関数(中間層)の勾配
ReLU関数は、以下でした。
f_{ReLU}(u) =
\left\{
\begin{array}{ll}
u & (u \gt 0) \\
0 & (u \le 0)
\end{array}
\right.
こちらの微分は簡単ですね。
f_{ReLU}^{'}(u) =
\left\{
\begin{array}{ll}
1 & (u \gt 0) \\
0 & (u \le 0)
\end{array}
\right.
実装です。
def relu_back(dz, u):
return dz * np.where(u > 0, 1, 0)
前の勾配、dzを掛けています。
Affine変換の勾配
例えば、$ u_1^{(3)} $は、以下の式となります。
u_1^{(3)} = w_{11}^{(3)}z_1^{(2)} + w_{12}^{(3)}z_2^{(2)} + w_{13}^{(3)}z_3^{(2)} + b_1^{(3)}
それぞれ偏微分してみます。偏微分を行う変数以外は定数とみなします。
\begin{align}
\frac{\partial u_1^{(3)}}{\partial z_1^{(2)}} &= w_{11}^{(3)}\\
\frac{\partial u_1^{(3)}}{\partial w_{11}^{(3)}} &= z_1^{(2)}\\
\frac{\partial u_1^{(3)}}{\partial b_1^{(3)}} &= 1
\end{align}
一般的には、$ u $を$ z $で偏微分すると$ z $に掛けた重みに、重みで偏微分すると重みに掛けた$ z $に、バイアスは、1ですね。
実装は、以下です。
def affine_back(du, z, W, b):
dz = np.dot(du, W.T)
dW = np.dot(z.T, du)
db = np.dot(np.ones(z.shape[0]).T, du)
return dz, dW, db
それぞれ$ u $の勾配を掛けることで、それ以前の勾配を掛けることになります。
重み調整
最後に、求めた勾配から重みを調整します。求めた勾配に、学習率lrを掛けて引きます。
\begin{align}
w^{(1)} &= w^{(1)} - lr * \frac{\partial E}{\partial w^{(1)}}\\
w^{(2)} &= w^{(2)} - lr * \frac{\partial E}{\partial w^{(2)}}\\
w^{(3)} &= w^{(3)} - lr * \frac{\partial E}{\partial w^{(3)}}
\end{align}
勾配が正であれば、値を小さくします。勾配が負であれば、値を大きくします。
学習全体
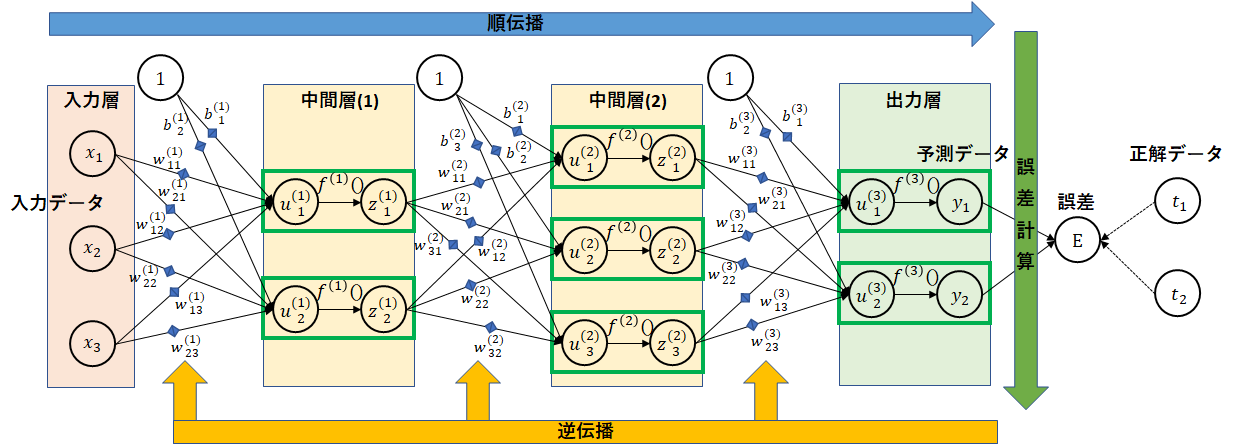
全体の流れをもう一度示します。
入力データから予測データを求めるまでを順伝播と言います。
中間層の2階層の実装は、以下です。
# 順伝播
u1 = affine(x, W1, b1)
z1 = relu(u1)
u2 = affine(z1, W2, b2)
z2 = relu(u2)
u3 = affine(z2, W3, b3)
y = softmax(u3)
逆に勾配の計算を求め、重みの更新を行う部分を逆伝播と言います。
# 逆伝播
dy = softmax_cross_entropy_error_back(y, t)
dz2, dW3, db3 = affine_back(dy, z2, W3, b3)
du2 = relu_back(dz2, u2)
dz1, dW2, db2 = affine_back(du2, z1, W2, b2)
du1 = relu_back(dz1, u1)
dx, dW1, db1 = affine_back(du1, x, W1, b1)
重みの更新です。
# 重み、バイアスの更新
W1 = W1 - lr * dW1
b1 = b1 - lr * db1
W2 = W2 - lr * dW2
b2 = b2 - lr * db2
W3 = W3 - lr * dW3
b3 = b3 - lr * db3
今回は、分かりやすくするため2階層固定としました。多階層とするには、W,b,u,zなどを配列とし、for分でループさせると任意の階層に対応できます。
プログラム全体
今回作成したプログラムの全体です。
関数部分
import numpy as np
# affine変換
def affine(z, W, b):
return np.dot(z, W) + b
# affine変換勾配
def affine_back(du, z, W, b):
dz = np.dot(du, W.T)
dW = np.dot(z.T, du)
db = np.dot(np.ones(z.shape[0]).T, du)
return dz, dW, db
# 活性化関数(ReLU)
def relu(u):
return np.maximum(0, u)
# 活性化関数(ReLU)勾配
def relu_back(dz, u):
return dz * np.where(u > 0, 1, 0)
# 活性化関数(softmax)
def softmax(u):
max_u = np.max(u, axis=1, keepdims=True)
exp_u = np.exp(u-max_u)
return exp_u/np.sum(exp_u, axis=1, keepdims=True)
# 誤差(交差エントロピー)
def cross_entropy_error(y, t):
return -np.sum(t * np.log(np.maximum(y,1e-7)))/y.shape[0]
# 誤差(交差エントロピー)+活性化関数(softmax)勾配
def softmax_cross_entropy_error_back(y, t):
return (y - t)/y.shape[0]
学習部分
def learn(x, t, W1, b1, W2, b2, W3, b3, lr):
# 順伝播
u1 = affine(x, W1, b1)
z1 = relu(u1)
u2 = affine(z1, W2, b2)
z2 = relu(u2)
u3 = affine(z2, W3, b3)
y = softmax(u3)
# 逆伝播
dy = softmax_cross_entropy_error_back(y, t)
dz2, dW3, db3 = affine_back(dy, z2, W3, b3)
du2 = relu_back(dz2, u2)
dz1, dW2, db2 = affine_back(du2, z1, W2, b2)
du1 = relu_back(dz1, u1)
dx, dW1, db1 = affine_back(du1, x, W1, b1)
# 重み、バイアスの更新
W1 = W1 - lr * dW1
b1 = b1 - lr * db1
W2 = W2 - lr * dW2
b2 = b2 - lr * db2
W3 = W3 - lr * dW3
b3 = b3 - lr * db3
return W1, b1, W2, b2, W3, b3
たったこれだけです。
これで、MNISTで約98%の正解率まで学習が可能です。
予測は、以下で行います。
def predict(x, W1, b1, W2, b2, W3, b3):
# 順伝播
u1 = affine(x, W1, b1)
z1 = relu(u1)
u2 = affine(z1, W2, b2)
z2 = relu(u2)
u3 = affine(z2, W3, b3)
y = softmax(u3)
return y
学習の実行
実行プログラム
実際に、MNISTで98%の正解率となるか確認するためのプログラムです。
今回の目的は、学習プログラムを作成することでしたので、詳細な説明はしません。(今後、ハイパーパラメータについてまとめたいと考えています。)
実行は、中間層2層、1階層目のノード数100、2階層目のノード数50で実行します。学習は、100データごとに、50回(50エポック)行います。
データは、MNISTのページからダウンロードしてください。
- train-images-idx3-ubyte.gz: 学習用画像
- train-labels-idx1-ubyte.gz: 学習用正解ラベル
- t10k-images-idx3-ubyte.gz: テスト用画像
- t10k-labels-idx1-ubyte.gz: テスト用正解ラベル
データは、c:\mnist\に格納することを想定しています。別のフォルダに格納した場合は、load_mnistのパラメータを変更してください。
import gzip
import numpy as np
# MNIST読み込み
def load_mnist( mnist_path ) :
return _load_image(mnist_path + 'train-images-idx3-ubyte.gz'), \
_load_label(mnist_path + 'train-labels-idx1-ubyte.gz'), \
_load_image(mnist_path + 't10k-images-idx3-ubyte.gz'), \
_load_label(mnist_path + 't10k-labels-idx1-ubyte.gz')
def _load_image( image_path ) :
# 画像データの読み込み
with gzip.open(image_path, 'rb') as f:
buffer = f.read()
size = np.frombuffer(buffer, np.dtype('>i4'), 1, offset=4)
rows = np.frombuffer(buffer, np.dtype('>i4'), 1, offset=8)
columns = np.frombuffer(buffer, np.dtype('>i4'), 1, offset=12)
data = np.frombuffer(buffer, np.uint8, offset=16)
image = np.reshape(data, (size[0], rows[0]*columns[0]))
image = image.astype(np.float32)
return image
def _load_label( label_path ) :
# 正解データ読み込み
with gzip.open(label_path, 'rb') as f:
buffer = f.read()
size = np.frombuffer(buffer, np.dtype('>i4'), 1, offset=4)
data = np.frombuffer(buffer, np.uint8, offset=8)
label = np.zeros((size[0], 10))
for i in range(size[0]):
label[i, data[i]] = 1
return label
# 正解率
def accuracy_rate(y, t):
max_y = np.argmax(y, axis=1)
max_t = np.argmax(t, axis=1)
return np.sum(max_y == max_t)/y.shape[0]
# MNISTデータ読み込み
x_train, t_train, x_test, t_test = load_mnist('c:\\mnist\\')
# 入力データの正規化(0~1)
nx_train = x_train/255
nx_test = x_test/255
# ノード数設定
d0 = nx_train.shape[1]
d1 = 100 # 1層目のノード数
d2 = 50 # 2層目のノード数
d3 = 10
# 重みの初期化(-0.1~0.1の乱数)
np.random.seed(8)
W1 = np.random.rand(d0, d1) * 0.2 - 0.1
W2 = np.random.rand(d1, d2) * 0.2 - 0.1
W3 = np.random.rand(d2, d3) * 0.2 - 0.1
# バイアスの初期化(0)
b1 = np.zeros(d1)
b2 = np.zeros(d2)
b3 = np.zeros(d3)
# 学習率
lr = 0.5
# バッチサイズ
batch_size = 100
# 学習回数
epoch = 50
# 予測(学習データ)
y_train = predict(nx_train, W1, b1, W2, b2, W3, b3)
# 予測(テストデータ)
y_test = predict(nx_test, W1, b1, W2, b2, W3, b3)
# 正解率、誤差表示
train_rate, train_err = accuracy_rate(y_train, t_train), cross_entropy_error(y_train, t_train)
test_rate, test_err = accuracy_rate(y_test, t_test), cross_entropy_error(y_test, t_test)
print("{0:3d} train_rate={1:6.2f}% test_rate={2:6.2f}% train_err={3:8.5f} test_err={4:8.5f}".format((0), train_rate*100, test_rate*100, train_err, test_err))
for i in range(epoch):
# 学習
for j in range(0, nx_train.shape[0], batch_size):
W1, b1, W2, b2, W3, b3 = learn(nx_train[j:j+batch_size], t_train[j:j+batch_size], W1, b1, W2, b2, W3, b3, lr)
# 予測(学習データ)
y_train = predict(nx_train, W1, b1, W2, b2, W3, b3)
# 予測(テストデータ)
y_test = predict(nx_test, W1, b1, W2, b2, W3, b3)
# 正解率、誤差表示
train_rate, train_err = accuracy_rate(y_train, t_train), cross_entropy_error(y_train, t_train)
test_rate, test_err = accuracy_rate(y_test, t_test), cross_entropy_error(y_test, t_test)
print("{0:3d} train_rate={1:6.2f}% test_rate={2:6.2f}% train_err={3:8.5f} test_err={4:8.5f}".format((i+1), train_rate*100, test_rate*100, train_err, test_err))
プログラムは、各実行回ごとに、学習データの正解率、テストデータの正解率、学習データの誤差、テストデータの誤差の順に表示しています。
実行結果
実行結果です。
0 train_rate= 11.67% test_rate= 12.18% train_err= 2.30623 test_err= 2.30601
1 train_rate= 92.39% test_rate= 92.38% train_err= 0.24541 test_err= 0.24307
2 train_rate= 96.78% test_rate= 96.34% train_err= 0.10314 test_err= 0.11774
3 train_rate= 97.67% test_rate= 97.02% train_err= 0.07395 test_err= 0.10026
4 train_rate= 98.03% test_rate= 97.06% train_err= 0.06057 test_err= 0.09716
5 train_rate= 98.34% test_rate= 97.18% train_err= 0.05275 test_err= 0.09951
6 train_rate= 98.65% test_rate= 97.30% train_err= 0.04209 test_err= 0.09596
7 train_rate= 98.51% test_rate= 96.95% train_err= 0.04488 test_err= 0.10893
8 train_rate= 98.79% test_rate= 97.39% train_err= 0.03560 test_err= 0.09737
9 train_rate= 99.01% test_rate= 97.47% train_err= 0.03033 test_err= 0.09725
10 train_rate= 99.12% test_rate= 97.57% train_err= 0.02574 test_err= 0.09797
11 train_rate= 99.16% test_rate= 97.47% train_err= 0.02525 test_err= 0.10192
12 train_rate= 99.38% test_rate= 97.67% train_err= 0.01840 test_err= 0.09298
13 train_rate= 99.44% test_rate= 97.70% train_err= 0.01623 test_err= 0.10091
14 train_rate= 99.17% test_rate= 97.52% train_err= 0.02395 test_err= 0.10848
15 train_rate= 99.53% test_rate= 97.76% train_err= 0.01352 test_err= 0.10865
16 train_rate= 99.48% test_rate= 97.68% train_err= 0.01517 test_err= 0.10646
17 train_rate= 99.63% test_rate= 97.84% train_err= 0.01055 test_err= 0.10101
18 train_rate= 99.19% test_rate= 97.48% train_err= 0.02559 test_err= 0.12495
19 train_rate= 99.68% test_rate= 97.83% train_err= 0.01083 test_err= 0.10719
20 train_rate= 99.72% test_rate= 97.87% train_err= 0.00812 test_err= 0.10383
21 train_rate= 99.17% test_rate= 97.40% train_err= 0.02394 test_err= 0.13422
22 train_rate= 99.66% test_rate= 97.90% train_err= 0.00967 test_err= 0.11079
23 train_rate= 99.64% test_rate= 97.65% train_err= 0.01141 test_err= 0.11507
24 train_rate= 99.84% test_rate= 97.91% train_err= 0.00505 test_err= 0.11271
25 train_rate= 99.83% test_rate= 97.81% train_err= 0.00559 test_err= 0.11566
26 train_rate= 99.97% test_rate= 98.06% train_err= 0.00120 test_err= 0.10587
27 train_rate=100.00% test_rate= 98.16% train_err= 0.00046 test_err= 0.10365
28 train_rate=100.00% test_rate= 98.14% train_err= 0.00028 test_err= 0.10521
29 train_rate=100.00% test_rate= 98.16% train_err= 0.00020 test_err= 0.10636
30 train_rate=100.00% test_rate= 98.14% train_err= 0.00017 test_err= 0.10702
31 train_rate=100.00% test_rate= 98.16% train_err= 0.00015 test_err= 0.10763
32 train_rate=100.00% test_rate= 98.17% train_err= 0.00014 test_err= 0.10802
33 train_rate=100.00% test_rate= 98.19% train_err= 0.00013 test_err= 0.10863
34 train_rate=100.00% test_rate= 98.18% train_err= 0.00012 test_err= 0.10904
35 train_rate=100.00% test_rate= 98.17% train_err= 0.00011 test_err= 0.10938
36 train_rate=100.00% test_rate= 98.18% train_err= 0.00010 test_err= 0.10971
37 train_rate=100.00% test_rate= 98.19% train_err= 0.00009 test_err= 0.11007
38 train_rate=100.00% test_rate= 98.18% train_err= 0.00009 test_err= 0.11035
39 train_rate=100.00% test_rate= 98.19% train_err= 0.00008 test_err= 0.11066
40 train_rate=100.00% test_rate= 98.19% train_err= 0.00008 test_err= 0.11096
41 train_rate=100.00% test_rate= 98.19% train_err= 0.00008 test_err= 0.11121
42 train_rate=100.00% test_rate= 98.20% train_err= 0.00007 test_err= 0.11134
43 train_rate=100.00% test_rate= 98.20% train_err= 0.00007 test_err= 0.11166
44 train_rate=100.00% test_rate= 98.20% train_err= 0.00007 test_err= 0.11189
45 train_rate=100.00% test_rate= 98.20% train_err= 0.00007 test_err= 0.11215
46 train_rate=100.00% test_rate= 98.19% train_err= 0.00006 test_err= 0.11237
47 train_rate=100.00% test_rate= 98.20% train_err= 0.00006 test_err= 0.11256
48 train_rate=100.00% test_rate= 98.20% train_err= 0.00006 test_err= 0.11272
49 train_rate=100.00% test_rate= 98.22% train_err= 0.00006 test_err= 0.11297
50 train_rate=100.00% test_rate= 98.22% train_err= 0.00006 test_err= 0.11314
26回目で、テストデータに対する正解率は、98%を超えました。
最後にもう一度言います。信じられないかもしれませんが、たった数十ステップで98%を超える正解率になりました。
別に、1,2などの数字の形状を教えたわけではありません。自分で学習しました。○△×でもアルファベットでもプログラムを変更なしで、そのまま学習できます。また、画像でなくても数値データであれば入力データから予測が可能となります。
最初にも書きましたが、このプログラムは、ディープラーニング(ニューラルネットワーク)を理解するためのものです。大きなデータやデータによっては対応できません。どんなデータでも対応できるわけではありません。その点の理解をお願いします。
改版履歴
2018/6/23 入力データの正規化、重みの初期化を単純化