概要
高校生の時は**「三角関数とか何の役に立つんですか~?」側の生徒でした。
後になって学びなおして苦労しました。sin cosをちゃんと理解するには「回る」という事は具体的にどういう事なのか?**とか、**三角比が成り立つのは何故なのか?**を考えないといけないです。
いまでもちゃんと説明できるか?と言われたら怪しいですが、似たような悩みを抱えた人のヒントになればいいなと思い書きます。
ただし、この記事はあくまで**「UnityでSin関数を扱えるようになる」**を目指したものです。
なので説明の仕方はその目的に絞ったものになります。
Sin関数のイメージ
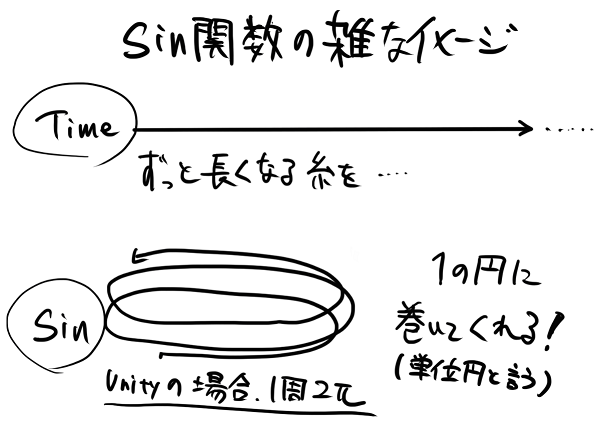
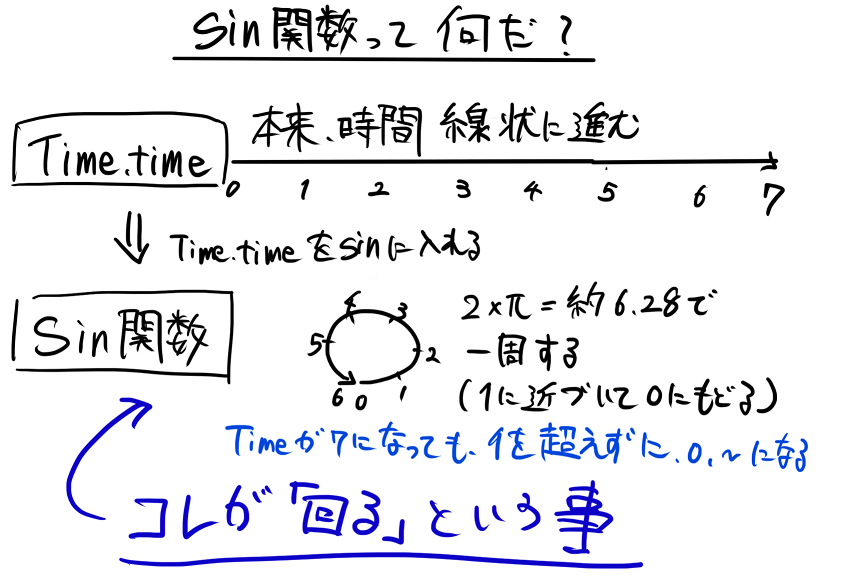
「時間」という概念は1秒2秒3秒…と1つの方向に進み続けます。基本は戻ったりしません。
図形にした場合、ずっと長くなりつづける糸のようなものです。
それに対して、Sin関数は…
sin関数に値を入れてやると「その値が単位円のどの位置になるか?」を求めます。
抽象的に例えるなら、Sin関数は**「半径1の棒に、Timeの糸をぐるぐると巻き付けて、巻き終わった位置を教えてくれる」**ような仕事をこなしてくれます。
Unityのコードにしてみる
Time
Time.time;
これで「ゲームを開始してから現在のフレームまでかかった時間」を求める事ができます。
これが「長くなりつづける糸」です。
Sin関数(Mathf.sin)
float sin = Mathf.Sin(Time.time);
UnityでSin関数を使う場合は「Mathf.Sin()」と書きます。
Time.timeをSinに渡してやる事で、1の円に巻き付けた結果 sin を返してくれます。
sinの結果は常に-1~1の値です。
Sin関数の何がうれしいのか?
で!「Time.time」を「sin関数」に突っ込んだら時間の長さに応じた「円の位置になる」のは分かったけど…
それの何がうれしいのさ?という話です。ここから本題です。
周期的な運動が作れる
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
public class LoopMotion : MonoBehaviour {
void Update ()
{
float sin = Mathf.Sin(Time.time);
this.transform.position = new Vector3(0,sin,0);
}
}
「this.transform.position」はこのオブジェクトの座標
「new Vector3(0,sin,0)」はX座標が0 Y座標がSin Z座標が0となるベクトルです。
まず float sin は-1~1の間で、Timeが変化する毎に振幅するように変化します。
その値を使ってオブジェクトの高さを決めてやれば、上下に移動するオブジェクトのできあがりです。
このようにする事で、キーを打ってアニメーションを作らなくてもアニメーションが作れますし、sinの値を2倍にすれば移動量を変化させたり、Time.timeの値を倍にすれば振幅速度を早くしたり、動的な変化を加える事ができます。
キーフレームでのアニメーションでは難しい動的な制御に欠かせない存在です。(自動でカメラを回したいなど)
また、時間を使って色(RGB値)を変化させた場合、時間をそのまま使うとすぐ1に達してしまい扱いに不便です。
時間の領域を-1~1にとどめる事で、扱いやすくします。
sin関数を自由に制御したい
float sin = Mathf.Sin(Time.time);
上の式でも十分回りますが…
「1秒間に5往復するようにしてほしい」とか、「1往復するのに5秒かかるようにしてほしい」と願うのが人間です。
その願いをコードにするにはどうすればいいでしょうか。
ひとまず…Time.timeに2を掛けてやれば時間の進み具合が2倍になるので、往復速度はあがる気がするし、逆に**0.5を掛けたら半分になるので、1往復するのに時間を必要とする…**のはイメージできるけど、具体的にどういう計算をすればいいか…?という問題ですが
答えからいいますと…こういう式になります。
float T = 1.0f;
float f = 1.0f / T;
float sin = Mathf.Sin(2 * Mathf.PI * f * Time.time);
2 × Mathf.PI (π)
何故「2 × π」なのか?といいますと…(Mathf.PIは円周率という意味です)
先ほど言った通りsin関数は**「単位円(半径1の円)という棒に時間という糸を巻くような処理」です。
この棒を一周するのに必要な糸の長さは…「棒の直径 × π」で求める事ができます。
なので 2 * Mathf.PI と書いてやればsin関数が一周するのに必要な糸の長さになります。
これに時間を掛けてやると…1秒したら1周、2秒したら2周という挙動にできます。
値が扱いやすくなりましたね!**
データを扱いやすくする処理を正規化とか言ったります。
この部分は「時間を円周に正規化した」と言ったりします。
f = 1 / T (Hz)
次に 「float f = 1 / T;」 は周波数(振動数)の公式です。
概念的には単純に…「1を何等分するか?」の公式みたいなものです。
なんかfとかTとか、周期とか角周波数オメガとか言われると難しそうですが、小学生にも分かるようにもっと簡単に言って欲しい!!!「1という数字をいくつに分けるか?」の定義だと!!!!
float sin = Mathf.Sin(2 * Mathf.PI * f * Time.time);
サンプルのTには1が入ってます。なので… f=1 になるので…
float sin = Mathf.Sin(2 * Mathf.PI * 1 * Time.time);
こういう事になります T=1の時は、Timeが1になると1周しますよね?
では、T=2の場合を見ましょう。
float sin = Mathf.Sin(2 * Mathf.PI * 0.5 * Time.time);
T=1 の時は f = 0.5 になり Timeが1になると0.5周しますよね?
1周するにはTimeが2になる必要があるので**「2秒で1周する」という式になりました。
この式にする事によって「T=1周に必要な秒数」**となり…
見事、Sin関数を操作できるようになりました!!!めでたい!!!
またf=1秒間あたりの周波数なので、fの値を変えてあげれば「1秒あたりの周波数」を調整できます。
これを知れば「1周に必要な秒数」と「1秒あたりの周波数」の両方でsin関数を調整する事ができます。
振動数 - Wikipedia / 周波数 - Wikipedia
まとめ
Timeをそのまま何かの処理に使った場合、値は永遠と大きくなるので扱いが難しいとおもいます。
例えば、sinを使わずに周期的な変化を作る場合、何かのフラグを用意して、timeを定期的にリセットしてその間に任意の処理を走らせる必要があるわけです。
考え方としてはやや煩雑です。
(作ってる物がししおどしに似ていて、回転の本質は外してないが形がよくない。)
しかし**sin関数の結果なら「-1~1の範囲を出る事が無い」**ので、処理で使うには扱いやすいわけです。
sin関数を使えば、シェーダーで周期的な変化を作ったり、音を作ったり、様々な事に応用可能です。
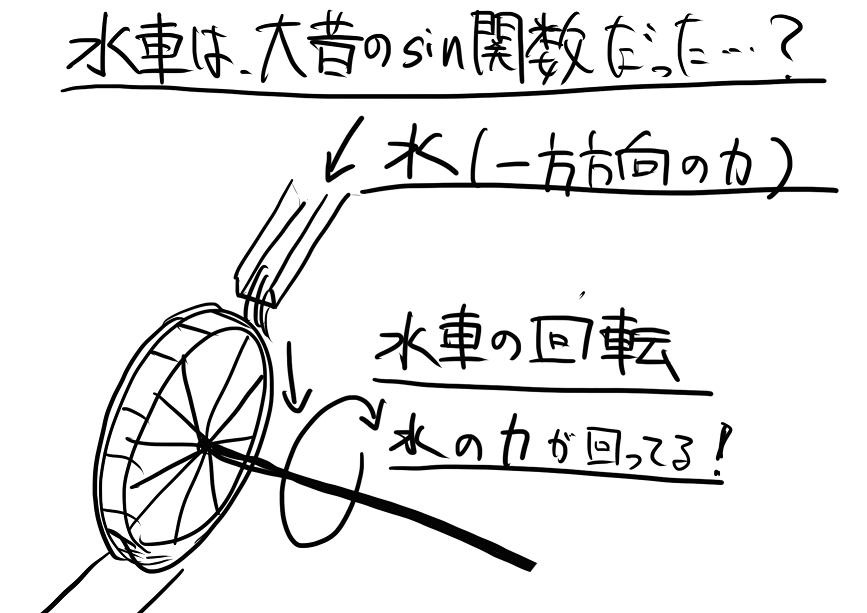
きっと、木槌で何かを潰す仕事をしてた人が、川の流れをみていて(この川の力を木槌の力にできね~っぺか)と思い、川を眺めながら休憩してたんだろうなぁ…と思う。
川の流れから、動力を得る気付きができるようになりたい。