導入

地図アプリとか乗換案内アプリとか、移動する時にコストを考えないといけない場合の探索はダイクストラ法が使われるんですって
で、実行したら出来たわけですが、

その過程がわかりにくいので見えたい
座標がバラバラでコンソール表示がつらい

という理由から可視化しました

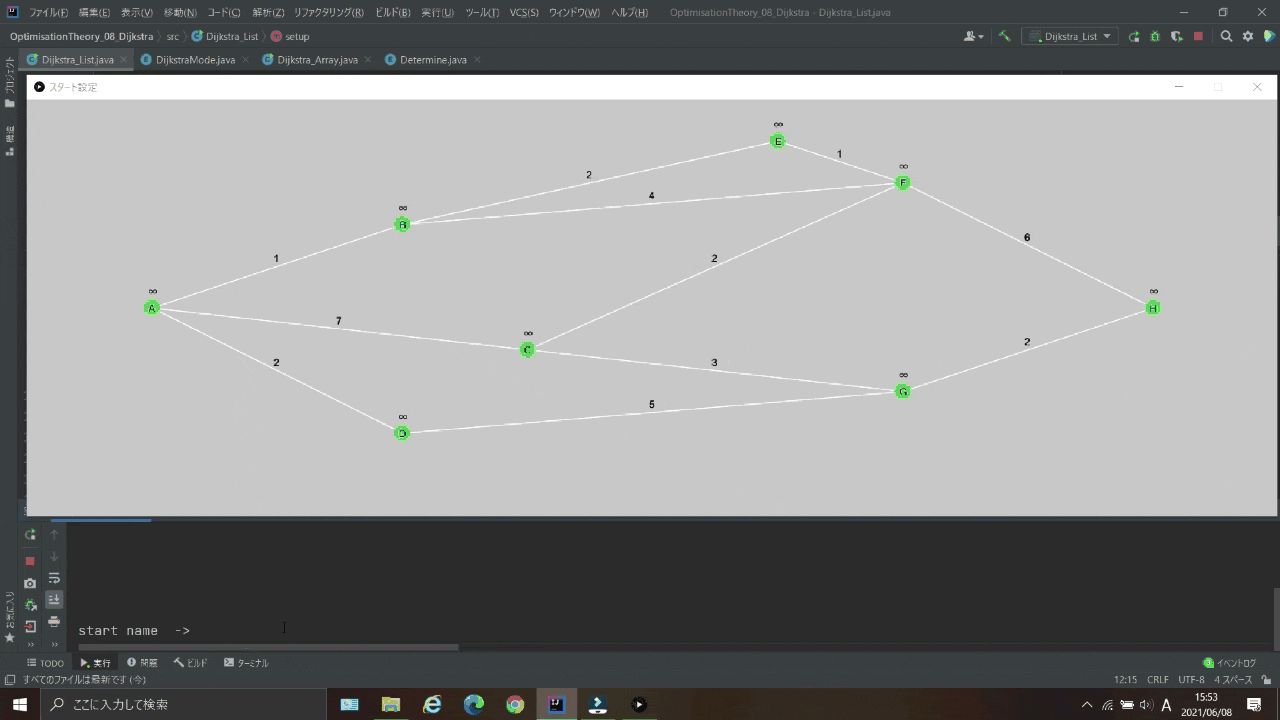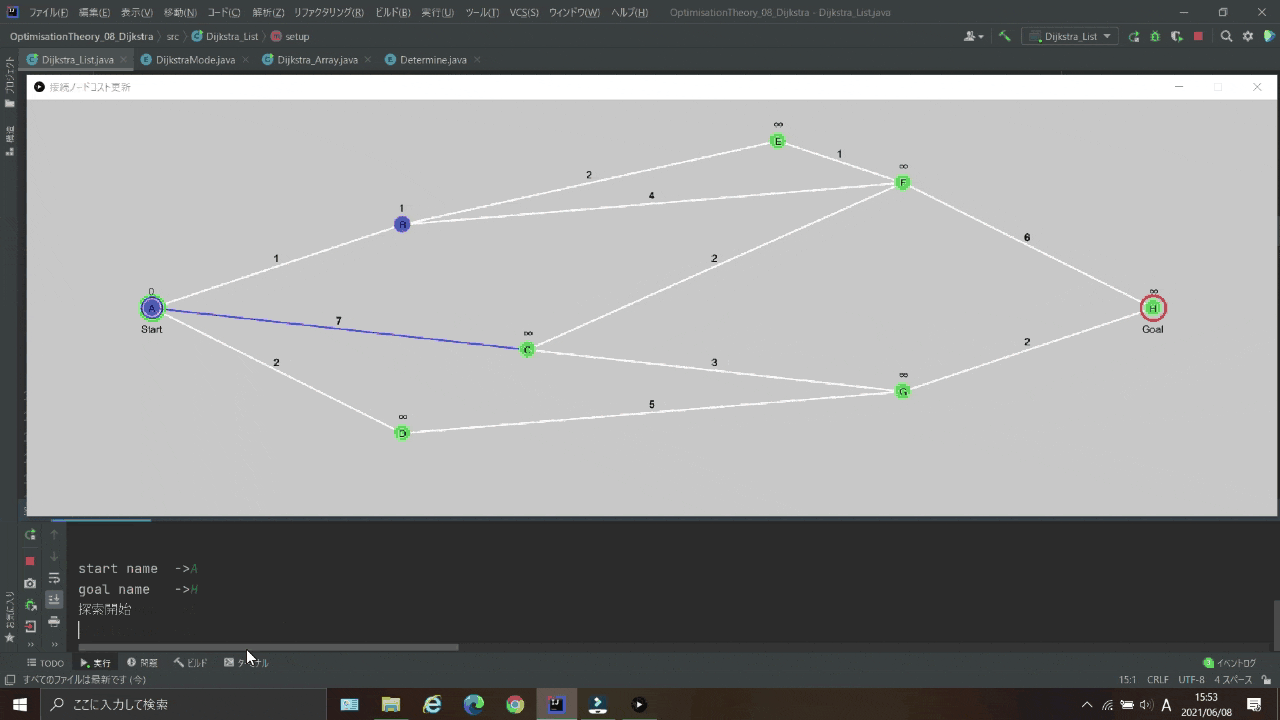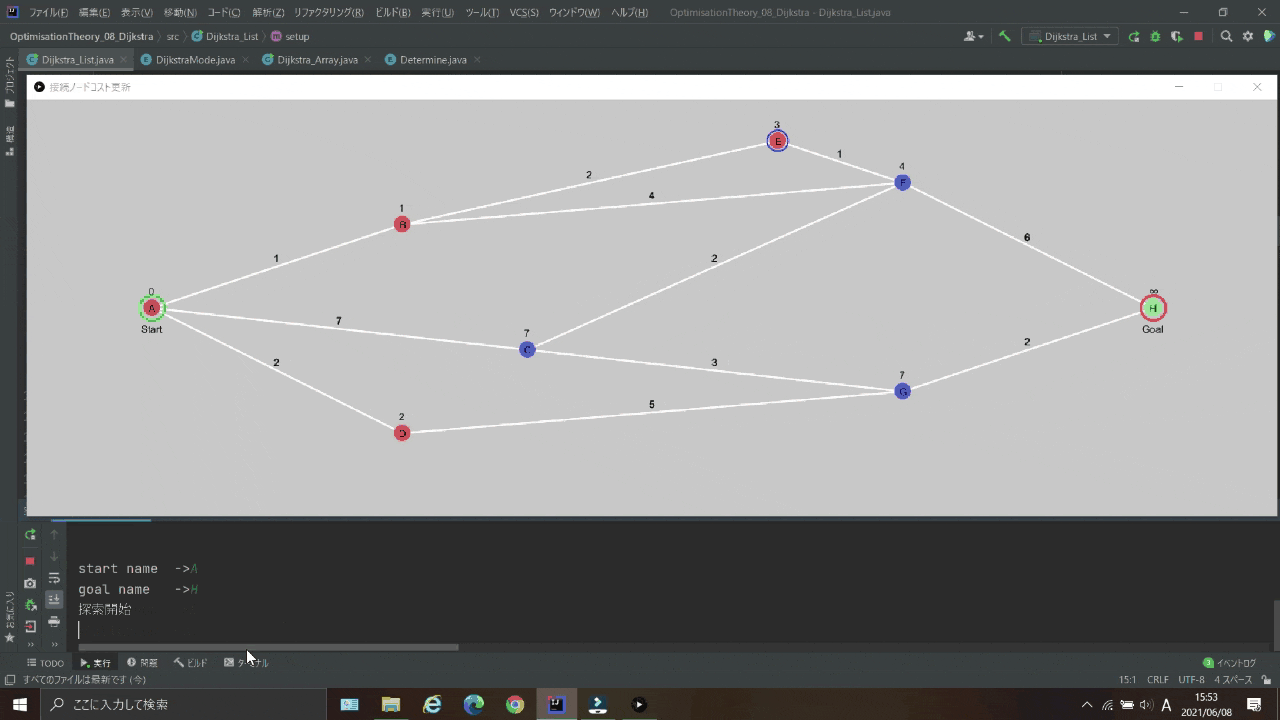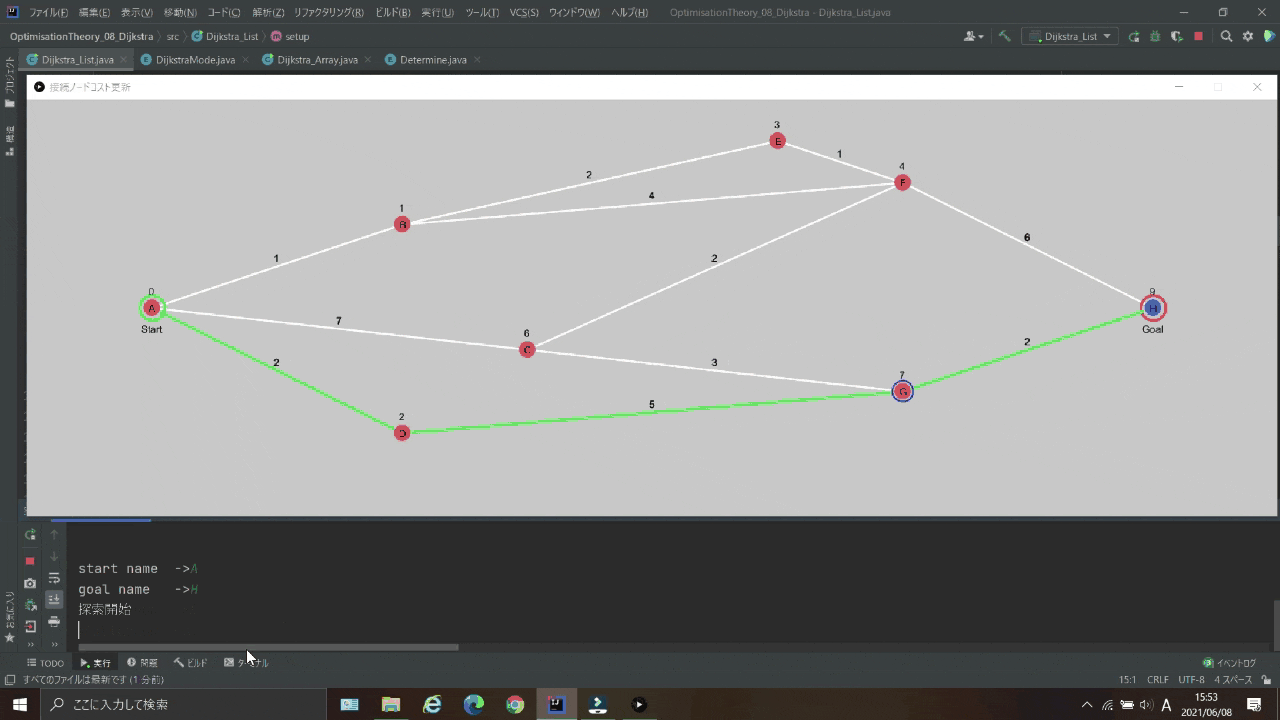
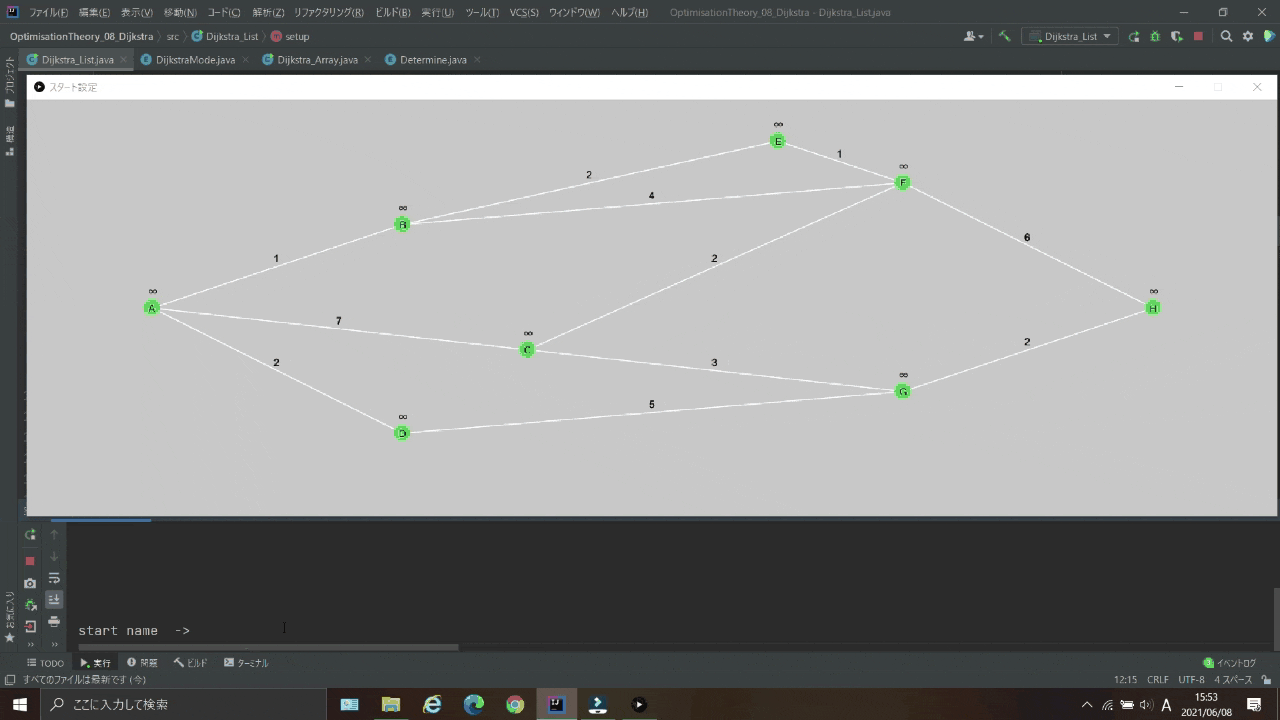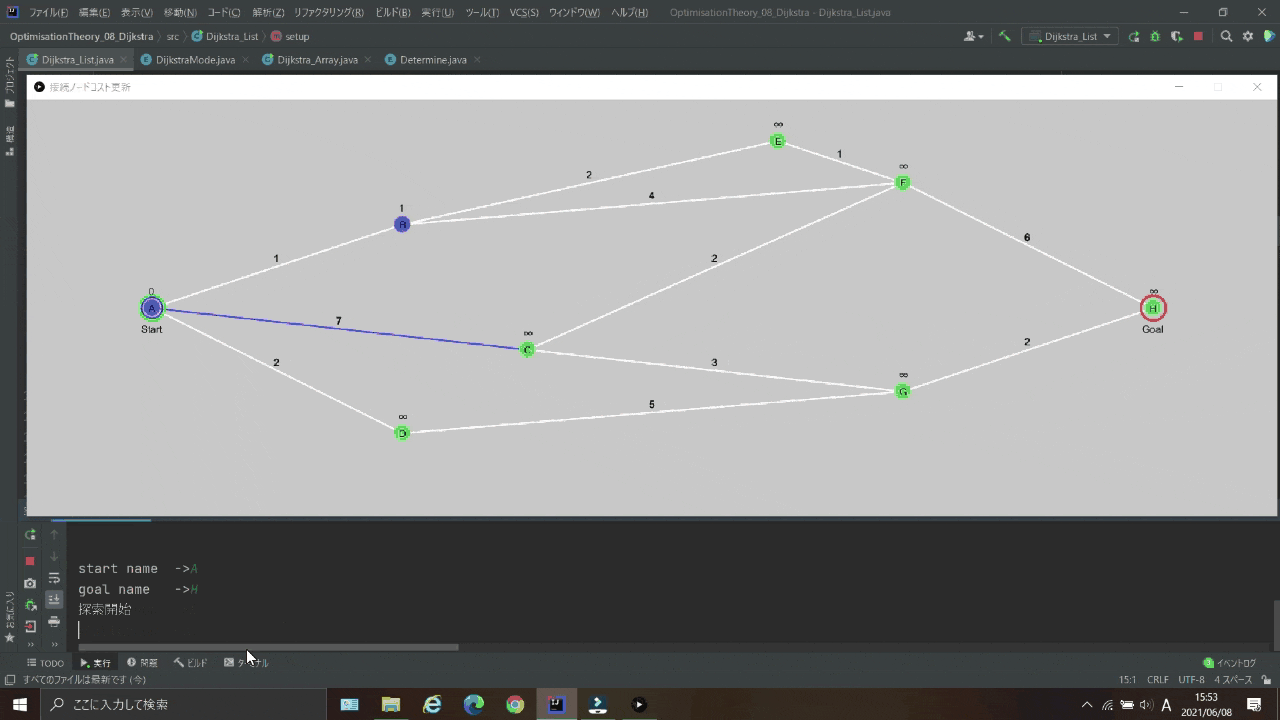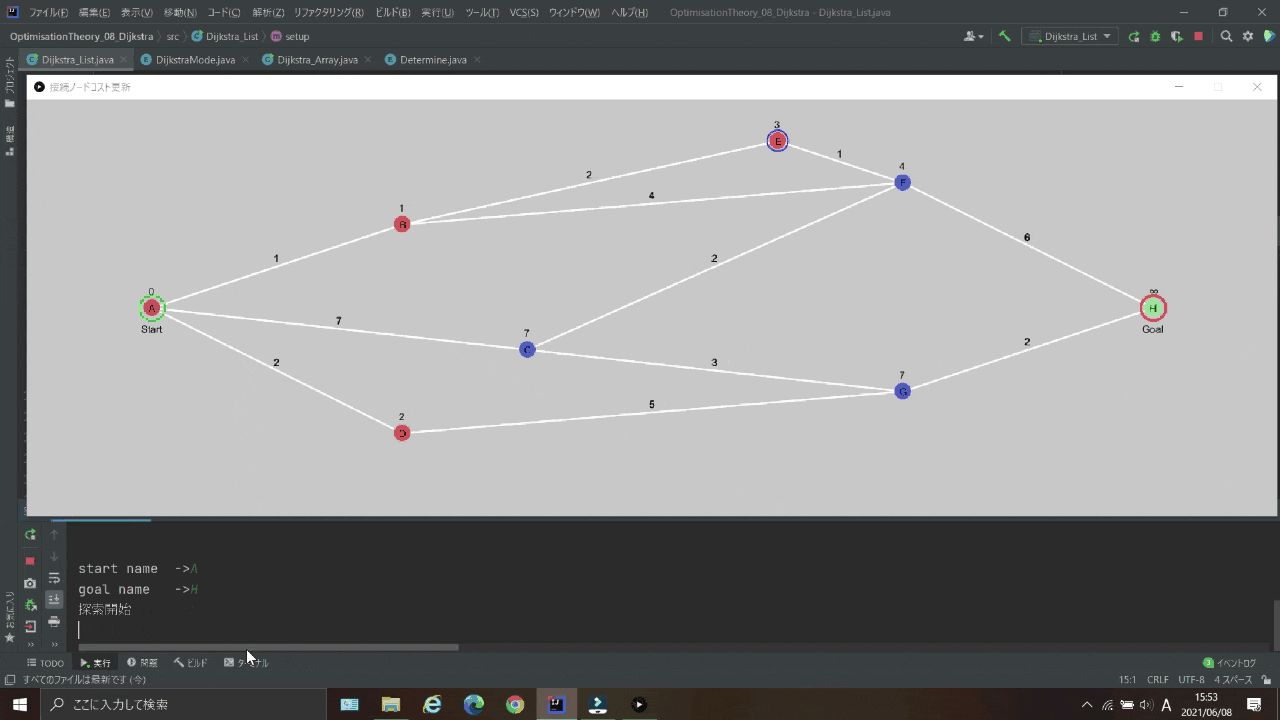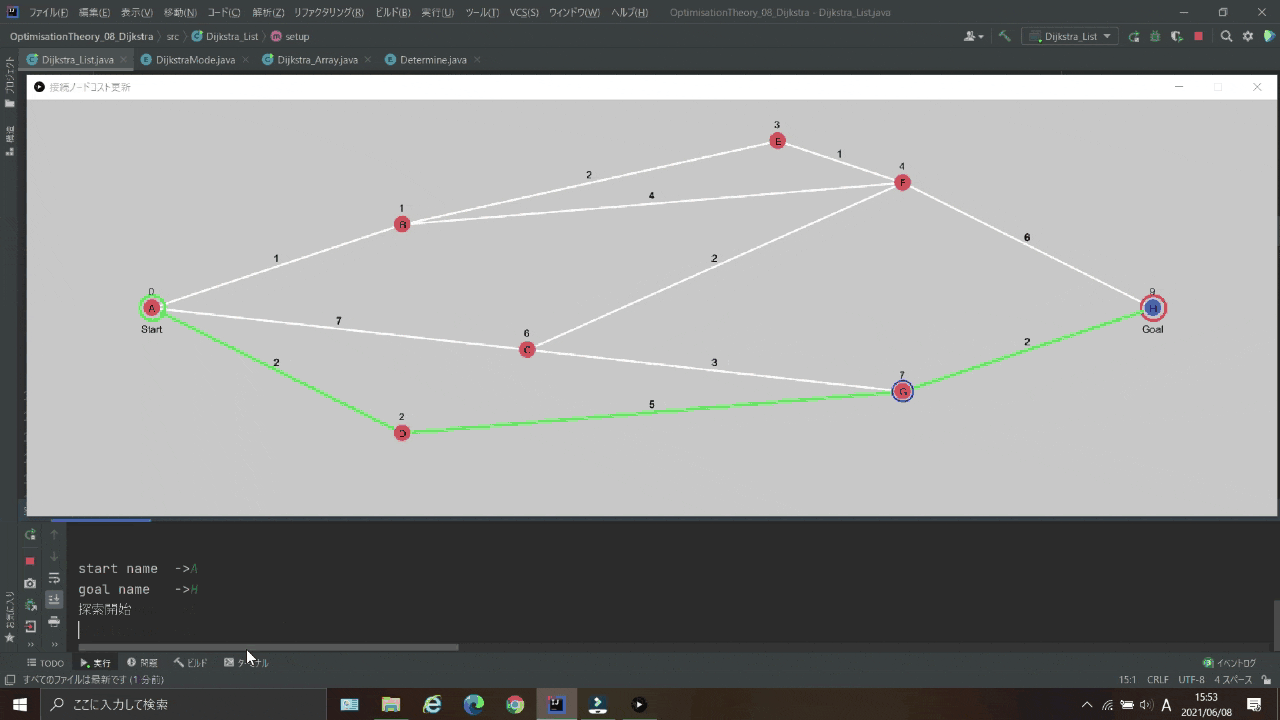
実行結果

解説

状況	画像
スタート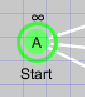
ゴール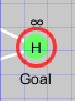
未探索のノード緑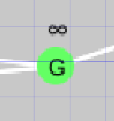
探索中のノード青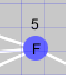
探索済のノード赤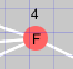
移動コスト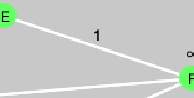
ノードまでの最小コスト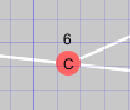
探索対象ノード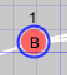
探索先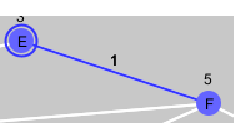
最小コスト経路

に変化させながら探索してます

入力

スタート地点、ゴール地点、探索終了後にもう1回探索するか(y or n)

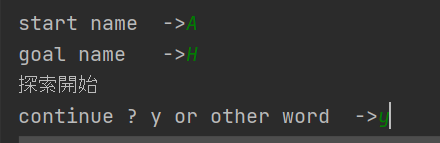
参考

processing導入の参考サイト

IntelliJ IDEAでProcessingを書く

グラフ（マップ）とダイクストラ法の手順の参考

ダイクストラ (Dijkstra) 法

ソースコード

内訳

Processingを実行する都合上、処理は1つのクラスに全部押込みました
内訳を説明すると

Nodeクラス
Edgeクラス
グローバル変数
メインメソッド（影薄い）
Processing
1. settting()
2. setup()
3. draw()ここでダイクストラ法を順々に実行
特に重要じゃないメソッド
マップの状況を描くメソッド

合計：258行
~~300行いってないのでセーフ~~

コード

Dijkstra_List

Dijkstra_List.java

import processing.core.*;

import java.util.ArrayList;
import java.util.Scanner;

//processing導入の参考サイト
//https://qiita.com/shion1118/items/49b803b3217e642cfbd1
//グラフの参考
//https://nw.tsuda.ac.jp/lec/dijkstra/
public class Dijkstra_List extends PApplet {
    private class Node {
        String name;//ノード名
        int cost;//最小コスト
        Node minFrom;//最短距離の来た道
        ArrayList<Edge> edge;//エッジのリスト
        Determine determine;//確定状況
        PVector pos;//位置

        Node(String name, PVector pos) {
            this.name = name;
            this.pos = new PVector(pos.x * width, pos.y * height);
            cost = Integer.MAX_VALUE;
            edge = new ArrayList<>();
            determine = Determine.未確定;
        }

        @Override
        public String toString() {
            return getColor() + name + "\u001b[00m";
        }

        public void draw() {
            fill(pColor());
            noStroke();
            ellipse(pos.x, pos.y, 20, 20);
            fill(0);
            text(name, pos.x, pos.y + 5);
            text((cost == Integer.MAX_VALUE ? "∞" : cost + ""), pos.x, pos.y - 15);
        }

        private String getColor() {
            StringBuilder str = new StringBuilder("\u001b[00;");
            switch (determine) {
                case 未確定 -> str.append("32");
                case 確定中 -> str.append("33");
                case 確定済 -> str.append("31");
            }
            return str.append("m").toString();
        }

        private int pColor() {
            return switch (determine) {
                case 未確定 -> color(100, 255, 100);
                case 確定中 -> color(100, 100, 255);
                case 確定済 -> color(255, 100, 100);
            };
        }
    }

    public class Edge {
        final Node TO;
        final int COST;
        Edge(int cost, Node to) {
            this.COST = cost;
            this.TO = to;
        }
    }

    Scanner sc;
    Node[] graph;
    int start = -1, goal = -1;
    Node currentNode;
    int searchEdgeIndex = -1;
    DijkstraMode flow = DijkstraMode.スタート設定;

    public static void main(String[] args) {
        PApplet.main("Dijkstra_List");
    }

    @Override
    public void settings() {
        size(1500, 500);//windowサイズ
    }

    @Override
    public void setup() {
        frameRate(2);
        getSurface().setAlwaysOnTop(true);//windowを常に前面にする
        textAlign(CENTER);
        sc = new Scanner(System.in);
        init();
    }

    void init() {
        setData();
        start = goal = searchEdgeIndex = -1;
        currentNode = null;
        flow = DijkstraMode.スタート設定;
        printMap();
    }

    @Override
    public void draw() {
        switch (flow) {
            case スタート設定 -> {
                while ((start = searchName(input("start name"))) == -1) {
                    for (Node n : graph) System.out.print(n.name + " ");
                    System.out.println("：の中から選んでください");
                }
                flow = DijkstraMode.ゴール設定;
            }
            case ゴール設定 -> {
                while ((goal = searchName(input("goal name"))) == -1) {
                    for (Node n : graph) System.out.print(n.name + " ");
                    System.out.println("：の中から選んでください");
                }
                System.out.println("探索開始");
                graph[start].cost = 0;
                flow = DijkstraMode.最短距離ノード設定;
            }
            case 最短距離ノード設定 -> {
                int minCostNode = minCost();
                if (minCostNode == -1) {
                    flow = DijkstraMode.ルート確定;
                    break;
                }
                currentNode = graph[minCostNode];
                currentNode.determine = Determine.確定中;
                searchEdgeIndex = 0;
                flow = DijkstraMode.接続ノードコスト更新;
            }
            case 接続ノードコスト更新 -> {
                Edge edge = currentNode.edge.get(searchEdgeIndex++);
                if (edge.TO.determine != Determine.確定済 && currentNode.cost + edge.COST < edge.TO.cost) {
                    edge.TO.determine = Determine.確定中;
                    edge.TO.cost = currentNode.cost + edge.COST;
                    edge.TO.minFrom = currentNode;
                    //System.out.println(currentNode + " to "+edge.TO +" cost"+ edge.TO.cost);
                }
                if (searchEdgeIndex >= currentNode.edge.size()) {
                    searchEdgeIndex = -1;
                    flow = DijkstraMode.ノードを確定;
                }
            }
            case ノードを確定 -> {
                currentNode.determine = Determine.確定済;
                flow = DijkstraMode.最短距離ノード設定;
            }
            case ルート確定 -> {
                if (input("continue ? y or other word").equals("y")) {
                    init();
                    return;
                } else exit();
            }
        }
        printMap();
    }

    int minCost() {
        int index = -1, min = Integer.MAX_VALUE;
        for (int i = 0; i < graph.length; i++) {
            if (graph[i].determine == Determine.確定済) continue;
            if (graph[i].cost >= min) continue;
            min = graph[i].cost;
            index = i;
        }
        return index;
    }

    void setData() {
        graph = new Node[8];
        graph[0] = new Node("A", new PVector(0.1f, 0.5f));
        graph[1] = new Node("B", new PVector(0.3f, 0.3f));
        graph[2] = new Node("C", new PVector(0.4f, 0.6f));
        graph[3] = new Node("D", new PVector(0.3f, 0.8f));
        graph[4] = new Node("E", new PVector(0.6f, 0.1f));
        graph[5] = new Node("F", new PVector(0.7f, 0.2f));
        graph[6] = new Node("G", new PVector(0.7f, 0.7f));
        graph[7] = new Node("H", new PVector(0.9f, 0.5f));
        setBranch(0, 1, 1);
        setBranch(0, 2, 7);
        setBranch(0, 3, 2);
        setBranch(1, 4, 2);
        setBranch(1, 5, 4);
        setBranch(2, 5, 2);
        setBranch(2, 6, 3);
        setBranch(3, 6, 5);
        setBranch(4, 5, 1);
        setBranch(5, 7, 6);
        setBranch(6, 7, 2);
    }

    void setBranch(int from, int to, int cost) {
        graph[from].edge.add(new Edge(cost, graph[to]));
        graph[to].edge.add(new Edge(cost, graph[from]));
    }

    int searchName(String name) {
        for (int i = 0; i < graph.length; i++) if (graph[i].name.equals(name)) return i;
        return -1;
    }

    String input(String name) {
        System.out.print(name + "\t->");
        return sc.next();
    }

    void printMap() {
        background(200);
        for (Node node : graph) for (Edge edge : node.edge) edgeLine(node, edge, color(255));//エッジを描画
        if (searchEdgeIndex != -1) { //接続してるノードのコストを更新する様子の線
            edgeLine(currentNode, currentNode.edge.get(searchEdgeIndex), color(50, 50, 255));
        }
        if (start != -1) {//スタート地点をマーク
            noFill();
            stroke(50, 255, 50);
            strokeWeight(3);
            ellipse(graph[start].pos.x, graph[start].pos.y, 30, 30);
            text("Start", graph[start].pos.x, graph[start].pos.y + 30);
        }
        if (goal != -1) {
            noFill();
            stroke(255, 50, 50);
            strokeWeight(3);//ゴール地点をマーク
            ellipse(graph[goal].pos.x, graph[goal].pos.y, 30, 30);
            text("Goal", graph[goal].pos.x, graph[goal].pos.y + 30);

            if (graph[goal].minFrom != null) {//ゴールへのルートがある場合は表示
                stroke(color(100, 255, 100));
                strokeWeight(4);
                for (Node n = graph[goal]; n.minFrom != null; n = n.minFrom)
                    line(n.pos.x, n.pos.y, n.minFrom.pos.x, n.minFrom.pos.y);
            }
        }
        if (currentNode != null) {//最短距離を確定させるノードをマーク
            noFill();
            stroke(50, 50, 255);
            strokeWeight(2);
            ellipse(currentNode.pos.x, currentNode.pos.y, 25, 25);
        }
        //各ノードを表示
        for (Node node : graph) node.draw();
        //進行モードを表示
        getSurface().setTitle(flow.name());
    }

    void edgeLine(Node node, Edge edge, int color) {
        PVector center = node.pos.copy().add(edge.TO.pos).mult(0.5f);
        stroke(color);
        line(node.pos.x, node.pos.y, edge.TO.pos.x, edge.TO.pos.y);
        fill(0);
        text(edge.COST, center.x, center.y - 5);
    }

}

DijkstraMode

DijkstraMode.java

public enum DijkstraMode {
    スタート設定, ゴール設定, 最短距離ノード設定, 接続ノードコスト更新, ノードを確定, ルート確定
}

Determine

Determine.java

public enum Determine {
    未確定, 確定中, 確定済
}

まとめ

結果だけ得るよりも、途中経過を得る方がアルゴリズムがよく理解できるような気がします

苦労した点

ダイクストラ法をアニメーションするために処理を分割する
文字サイズや色

アルゴリズムに関係ない所で苦労します。本当にありがとうございました。

[Processing]ダイクストラ法の探索を可視化

導入