誤差逆伝播法とは
どうもNegimaruです。今回は誤差逆伝播法について整理していきます。誤差逆伝播法とは、ニューラルネットワークの学習において勾配を求めるのに使われる手法のことです。コスト関数を各パラメータで偏微分した値を求めるために、出力側のノードから連鎖率を用いて勾配を計算していきます。基本的な仕組みが簡単なニューラルネットワークですが、誤差逆伝播法の計算は行列やベクトルの微分が登場するためハードルが高く感じる人が多いと思います。そこで、一度きちんと整理しておいて後から見直せるようにしておこうと思い、この投稿を書いています。この記事では分母レイアウトに沿って行列やベクトルの微分を表記します。文献によっては分子レイアウトと分母レイアウトを混同しているものもありますが、今回は混同しないように気を付けて書いていこうと思います。
分母レイアウト
分母レイアウトは行列微分学における2つの記法の1つです。誤差逆伝播法の数式を扱う前に、そこで用いられる分母レイアウトの記法の定義と公式について整理しておきます。ポイントは、「分母」レイアウトの名前の通り、演算の結果は微分の分母と同じ形になることです。ベクトルで微分するならそのベクトルの形、行列で微分するならその行列の形になります。
スカラー関数をベクトルで微分する
スカラー関数$f$を$n$次元ベクトル$x$で微分するときの表記の定義は次のようになります。
\frac{\partial f}{\partial x} = \begin{pmatrix} \frac{\partial f}{\partial x_{1}}\\\ \vdots\\\ \frac{\partial f}{\partial x_{n}}\end{pmatrix}
つまり$\frac{\partial f}{\partial x}$の形は$x$の形と同じになります。
スカラー関数を行列で微分する
スカラー関数$f$を$m \times n$行列$A$で微分するときの表記の定義は次のようになります。
$$\frac{\partial f}{\partial A} = \begin{pmatrix} \frac{\partial f}{\partial A_{11}} & \cdots & \frac{\partial f}{\partial A_{1n}} \\ \vdots & \ddots & \vdots \\ \frac{\partial f}{\partial A_{m1}} & \cdots & \frac{\partial f}{\partial A_{mn}} \end{pmatrix}$$
つまり、$\frac{\partial f}{\partial A}$の$(i, j)$成分は$f$を$A_{ij}$で微分したものとなり、$\frac{\partial f}{\partial A}$の形は$A$の形と同じになります。
誤差逆伝播法の演算
では、いよいよ誤差逆伝播法の演算を説明します。ニューラルネットワークを数式で表す際、入力行列$X$の各行を1つのデータとする場合と、各列を1つのデータとする場合があります。自分がこの記事を書く際に参考にした教材では各列を1つのデータとしていたので、その場合の演算について書いていきます。ですが、各行を1つのデータとしていると教材もあると思います。そこで、各行を1つのデータとする場合も今後追記するかもしれません(まだ未定ですが)。さて、データを列とする入力行列は次のような形になります。$x_{i}$は$n$次元の列ベクトルであり、$X$は$n \times m$行列となります。
X = \begin{pmatrix} x_{1} & x_{2} & \cdots & x_{m}\end{pmatrix}
隠れ層の演算
隠れ層では順方向の伝播の時は次のような演算が行われます。
Z = WX + b
A = g(Z)
$X$は前の層からの入力であり、 データ数を$m$、前の層の出力の次元(前の層のノードの数)を$n$とすれば$n \times m$行列になります。各データが各列に対応しているからです。$W$は重み行列です。この層の出力の次元(この層のノードの数)を$l$とすれば$l \times n$行列になります。$b$は$l \times 1$行列です。ただし、全ての入力に対して足されるので、Pythonにおけるブロードキャストのようなことが行われて$l \times m$となって$WX$に足されます。gは活性化関数であり、シグモイド関数やReLU関数を表します。$A$はこの層の出力であり、$l \times m$行列です。$Z = WX + b$の次元がわかりやすいように図を描くと次のような感じです。
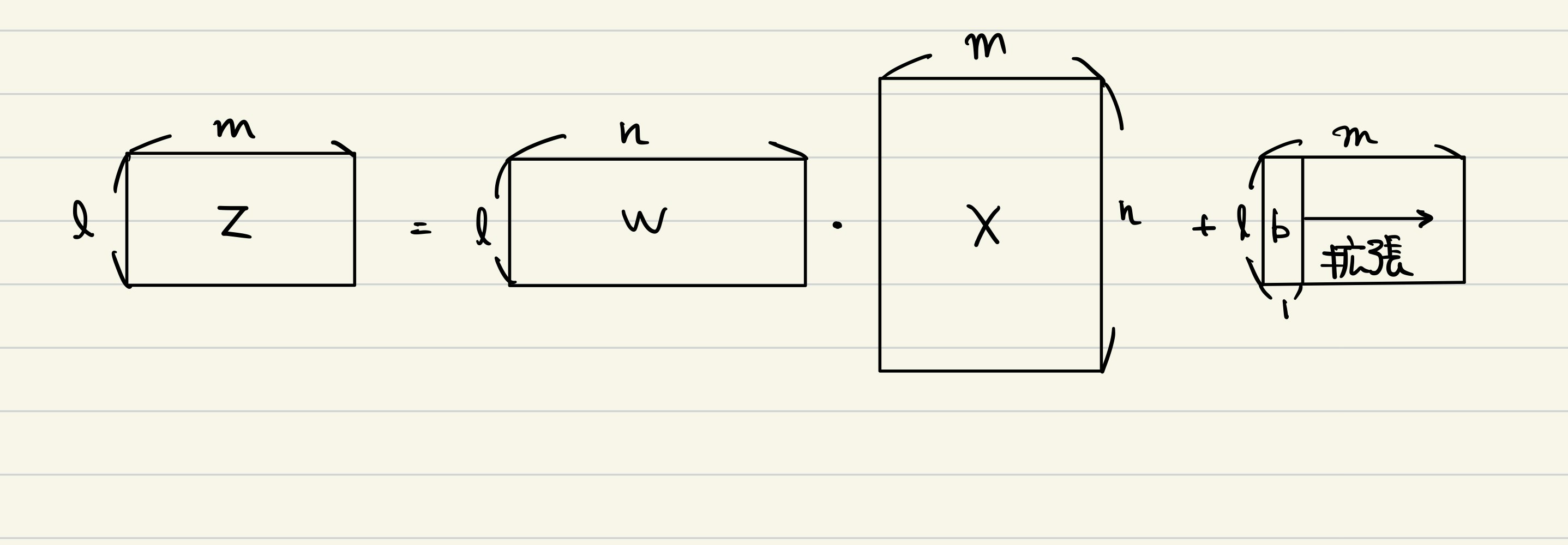
それでは、逆伝播について考えていきます。コスト関数の値を$J$として、$\frac{\partial J}{\partial A}$が既に求まっているとし、$\frac{\partial J}{\partial Z}$、$\frac{\partial J}{\partial W}$、$\frac{\partial J}{\partial b}$、$\frac{\partial J}{\partial X}$を計算します。
$$\begin{align*} \frac{\partial J}{\partial Z} &= \begin{pmatrix} \frac{\partial J}{\partial Z_{ij}} \end{pmatrix}
\\ &= \begin{pmatrix} \frac{\partial J}{\partial A_{ij}}\frac{\partial A_{ij}}{\partial Z_{ij}} \end{pmatrix}
\\ &= \begin{pmatrix} \frac{\partial J}{\partial A_{ij}}g'(Z_{ij}) \end{pmatrix}
\\ &= \frac{\partial J}{\partial A} * g'(Z)
\end{align*}$$
活性化関数$g$は$Z$の各要素に対して例えばシグモイド関数やReLU関数を適用します。したがって、$Z_{ij}$を変化させたときに$A$は$A_{ij}$しか変化しません。よって上の式のようにして$\frac{\partial J}{\partial Z}$は計算できます。$*$は要素ごとの積を表しています。さて、両辺の次元を確認してみましょう。$\frac{\partial J}{\partial Z}$は$Z$の次元と等しく、$(l, m)$です。$\frac{\partial J}{\partial A}$は$A$の次元と等しく$(l, m)$であり、$g'(Z)$は$(l, m)$なので両辺の次元が一致していることがわかります。この$\frac{\partial J}{\partial Z}$を用いて残りの勾配を計算します。
$$\begin{align*} \frac{\partial J}{\partial W} &= \begin{pmatrix} \frac{\partial J}{\partial W_{ij}} \end{pmatrix}
\\ &= \begin{pmatrix} \sum_{k=1}^m \frac{\partial J}{\partial Z_{ik}}\frac{\partial Z_{ik}}{\partial W_{ij}} \end{pmatrix}
\\ &= \frac{\partial J}{\partial Z}X^T
\end{align*}$$
$W_{ij}$を変化させると$Z_{ik}(1\le k\le m)$が変化することに注意すると、$\frac{\partial J}{\partial W}$は上式のように計算できます。$\frac{\partial J}{\partial W}$は$W$の次元と等しく、$(l, n)$です。$\frac{\partial J}{\partial Z}$は$Z$の次元と等しく$(l, m)$であり、$X^T$は$(m, n)$なので両辺の次元が一致していることが確認できます。
$$\begin{align*} \frac{\partial J}{\partial b} &= \begin{pmatrix} \frac{\partial J}{\partial b_{i1}} \end{pmatrix}
\\ &= \begin{pmatrix} \sum_{k=1}^m \frac{\partial J}{\partial Z_{ik}}\frac{\partial Z_{ik}}{\partial b_{i1}} \end{pmatrix}
\\ &= sum(\frac{\partial J}{\partial Z}, axis=1)
\end{align*}$$
$b_{i1}$を変化させると$Z_{ik}(1\le k\le m)$が変化することに注意すると、$\frac{\partial J}{\partial b}$は上式のように計算できます。ただし、$sum(\frac{\partial J}{\partial Z}, axis=1)$はNumPyの記法に従っていて、$\frac{\partial J}{\partial Z}$を行方向に足し合わせることで生成される$l \times 1$行列を表しています。$\frac{\partial J}{\partial b}$は$b$の次元と等しく、$(l, 1)$です。$sum(\frac{\partial J}{\partial Z}, axis=1)$の次元も$(l, 1)$なので両辺の次元は一致します。
$$\begin{align*} \frac{\partial J}{\partial X} &= \begin{pmatrix} \frac{\partial J}{\partial X_{ij}} \end{pmatrix}
\\ &= \begin{pmatrix} \sum_{k=1}^l \frac{\partial J}{\partial Z_{kj}}\frac{\partial Z_{kj}}{\partial X_{ij}} \end{pmatrix}
\\ &= \begin{pmatrix} \sum_{k=1}^l \frac{\partial J}{\partial Z_{kj}} W_{ki} \end{pmatrix}
\\ &= W^T\frac{\partial J}{\partial Z}
\end{align*}$$
$X_{ij}$を変化させると$Z_{kj}(1\le k\le l)$が変化することに注意すると、$\frac{\partial J}{\partial X}$は上式のように計算できます。$\frac{\partial J}{\partial X}$は$X$の次元と等しく、$(n, m)$です。$W^T$の次元は$(n, l)$であり、$\frac{\partial J}{\partial Z}$は$(l, m)$なので両辺の次元が一致していることが確認できます。これで、隠れ層の演算はおしまいです。演算が正しいことを確認するために等式の両辺の次元をチェックすることは大切です。慣れてくると次元から逆算して計算することもできます。
出力層の演算
続いて、隠れ層から出力層の演算について説明します。ここでは、二値分類において最後にシグモイド関数を使う場合について記述します。多値分類や回帰における演算については後日追記予定です。多値分類について2022/3/31に追記しました。
二値分類でシグモイド関数を用いる場合
このとき、順伝播では出力層において次のような演算が行われます。
$$\begin{align*}Z &= WX + b
\\ \hat{Y} &= Sigmoid(Z)
\\J &= \frac{1}{m}\sum_{i=1}^m L(\hat{y}^{(i)}, y^{(i)})
\\ &= \frac{1}{m}\sum_{i=1}^m -y^{(i)}log(\hat{y}^{(i)}) -(1-y^{(i)})log(1-\hat{y}^{(i)})
\end{align*}$$
$X$は前の層の出力です。データの数を$m$、前の層の次元を$n$とすれば、$X$の次元は$(n, m)$になります。$W$は重みです。出力層なのでその次元は$(1, n)$です。$b$の次元は$(1, 1)$ですが、隠れ層の時と同様にブロードキャストされて、$(1, m)$として計算されます。そして、$Z$と$\hat{Y}$は$(1, m)$となります。$\hat{Y}$の各要素は、i番目の入力データが1である確率の予測値に対応します。そして、コスト関数$J$は各データのLogistic lossの平均として定義されます。それでは、$\frac{\partial J}{\partial \hat{Y}}$、$\frac{\partial J}{\partial Z}$を計算していきましょう。$W$、$X$、$b$による偏微分の計算は隠れ層の時と同様なので省略します。
$$\begin{align*} \frac{\partial J}{\partial \hat{Y}} &= \begin{pmatrix} \frac{\partial J}{\partial Y_{1i}} \end{pmatrix}
\\ &= \begin{pmatrix} \frac{1}{m}( -\frac{y^{(i)}}{\hat{y}^{(i)}} + \frac{1 - y^{(i)}}{1 - \hat{y}^{(i)}}) \end{pmatrix}
\end{align*}$$
$\frac{\partial J}{\partial \hat{Y}}$はこのように計算できます。要素ごとの微分を考えれば普通に求まります。これを用いて$\frac{\partial J}{\partial Z}$を計算します。
\begin{align*} \frac{\partial J}{\partial Z} &= \begin{pmatrix} \frac{\partial J}{\partial Z_{1i}} \end{pmatrix}
\\\ &= \begin{pmatrix} \frac{\partial J}{\partial \hat{Y}_{1i}}\frac{\partial \hat{Y}_{1i}}{\partial Z_{1i}} \end{pmatrix}
\\\ &= \begin{pmatrix} \frac{1}{m}( -\frac{y^{(i)}}{\hat{y}^{(i)}} + \frac{1 - y^{(i)}}{1 - \hat{y}^{(i)}})\times \hat{y}^{(i)}(1 - \hat{y}^{(i)}) \end{pmatrix}
\\\ &= \frac{1}{m}(\hat{Y} - Y)
\end{align*}
とても綺麗な形になりました。ラベルが1である確率の予測値である$\hat{Y}$と正解ラベル$Y$が離れているほど勾配の絶対値が大きくなることもわかります。これは直感通りの結果であり、計算結果が正しそうだと確認できます。二値分類において二乗和誤差ではなく交差エントロピーを用いることが多い理由の1つはこのように綺麗に計算ができるからかもしれません。(主な理由は、おそらく、予測値と教師データが離れているときに交差エントロピーのほうが勾配が大きくなり学習が速く進むからです)。
多値分類でソフトマックス関数を用いる場合
ソフトマックス関数を出力層で用いるとき、順伝播は次のようになります。
$$\begin{align*}Z &= WX + b
\\ \hat{Y} &= Softmax(Z)
\\J &= \frac{1}{m}\sum_{i=1}^m L(\hat{y}^{(i)}, y^{(i)})
\\ &= \frac{1}{m}\sum_{i=1}^m (-\sum_{j=1}^C y_{j}^{(i)}log(\hat{y}_{j}^{(i)}))
\end{align*}$$
ただし、
Y = \begin{pmatrix} y^{(1)} & y^{(2)} & \cdots & y^{(m)}\end{pmatrix} \\
\hat{Y} = \begin{pmatrix} \hat{y}^{(1)} & \hat{y}^{(2)} & \cdots & \hat{y}^{(m)}\end{pmatrix}
とします。$X$は前の層の出力です。データの数を$m$、前の層の次元を$n$とすれば$X$の次元は$(n, m)$になります。$W$は重みです。クラスの数を$C$とすると、その次元は$(C, n)$となります。$b$の次元は$(C, 1)$ですが、ブロードキャストされて$(C, m)$になります。そして、$Z$と$\hat{Y}$は$(C, m)$になります。$\hat{Y}_{ji}$は$i$番目の入力データが$j$番目のクラスである確率の予測値となります。そしてコスト関数$J$は各データのSoftmax cross entropy lossの平均となります。それでは、$\frac{\partial J}{\partial \hat{Y}}$、$\frac{\partial J}{\partial Z}$を計算していきましょう。$W$、$X$、$b$による偏微分の計算は隠れ層の時と同様なので省略します。
$$\begin{align*} \frac{\partial J}{\partial \hat{Y}} &= \begin{pmatrix} \frac{\partial J}{\partial Y_{ij}} \end{pmatrix}
\\ &= \begin{pmatrix} \frac{1}{m}( -\frac{Y_{ij}}{\hat{Y}_{ij}}) \end{pmatrix}
\end{align*}$$
$\frac{\partial J}{\partial \hat{Y}}$は要素ごとの微分でなんなく求まりました。続いて、$\frac{\partial J}{\partial Z}$です。
\begin{align*} \frac{\partial J}{\partial Z} &= \begin{pmatrix} \frac{\partial J}{\partial Z_{ij}} \end{pmatrix}
\\\ &= \begin{pmatrix}\sum_{k=1}^{C} \frac{\partial J}{\partial \hat{Y}_{kj}}\frac{\partial \hat{Y}_{kj}}{\partial Z_{ij}} \end{pmatrix}
\\\ &= \begin{pmatrix} \sum_{k=1}^{C} (\frac{1}{m}(-\frac{Y_{kj}}{\hat{Y}_{kj}})(-\hat{Y}_{kj} \hat{Y}_{ij})) + \frac{1}{m}(-\frac{Y_{ij}}{\hat{Y}_{ij}}) \hat{Y}_{ij} \end{pmatrix}
\\\ &= \frac{1}{m}(\hat{Y} - Y)
\end{align*}
シグモイド関数を用いた二値分類のときと同じ形の結果が得られました。Softmax関数がSigmoid関数の拡張版であることを考えれば、自然な結果といえます。