概要
実数区間上の実数値関数に対して, 平均的な誤差を最小にする近似直線を求める方法を与える.
いくつかの適用例についても触れる.
Keywords: 最小二乗法, 残差平方和, 回帰直線
命題
実数区間 $[\alpha, \beta] \subset \mathbb{R} \quad (\alpha < \beta)$ 上で定義される性質の良い 1 実関数$f: [\alpha, \beta] \rightarrow \mathbb{R}$ に対して, 直線$ax+b$との残差平方和(の積分版)2
E(a,b) := \int_{\alpha}^{\beta}(f(x) - (ax+b))^2 dx
を最小化する$a, b$は以下の行列計算で求められる：
\begin{pmatrix}
a \\
b
\end{pmatrix}
=
\dfrac{12}{(\beta - \alpha)^3}
\begin{pmatrix}
-\dfrac{\alpha + \beta}{2} && 1 \\
\dfrac{\alpha^2 + \alpha \beta + \beta^2}{3} && -\dfrac{\alpha + \beta}{2}
\end{pmatrix}
\begin{pmatrix}
\int_{\alpha}^{\beta} f(x)dx \\
\int_{\alpha}^{\beta} x f(x)dx
\end{pmatrix}.
証明の概要
最小二乗法の導出と同じ発想で, $E(a,b)$の偏微分のゼロ点の方程式
\displaylines{
\dfrac{\partial E(a, b)}{\partial a} = \int_{\alpha}^{\beta} 2(f(x)-(ax+b))(-x)dx = 0 \\
\dfrac{\partial E(a, b)}{\partial b} = \int_{\alpha}^{\beta} 2(f(x)-(ax+b))dx = 0
}
を立て, $a, b$ について解く. ここで, 偏微分と積分とが交換可能である必要がある.
\displaylines{
\int_{\alpha}^{\beta}x f(x)dx = \int_{\alpha}^{\beta} x(ax+b)dx \\
\int_{\alpha}^{\beta}f(x)dx = \int_{\alpha}^{\beta}(ax+b) dx
}
より, 右辺をそれぞれ積分すると$a, b$ に関する連立一次方程式となり, $\alpha \neq \beta$であれば逆行列を求めることができて, 命題の式が導出される.
具体例
例1 二次関数
$f(x) = x^2$, $[\alpha, \beta] = [0, 1]$ とすると, $\int_0^1x^2dx = \frac{1}{3}, \int_0^1x x^2dx = \frac{1}{4}$ より,
\begin{pmatrix}
a \\
b
\end{pmatrix}
=
12
\begin{pmatrix}
-\dfrac{1}{2} && 1 \\
\dfrac{1}{3} && -\dfrac{1}{2}
\end{pmatrix}
\begin{pmatrix}
\dfrac{1}{3} \\
\dfrac{1}{4}
\end{pmatrix}
= \begin{pmatrix}
1 \\
-\dfrac{1}{6}
\end{pmatrix}
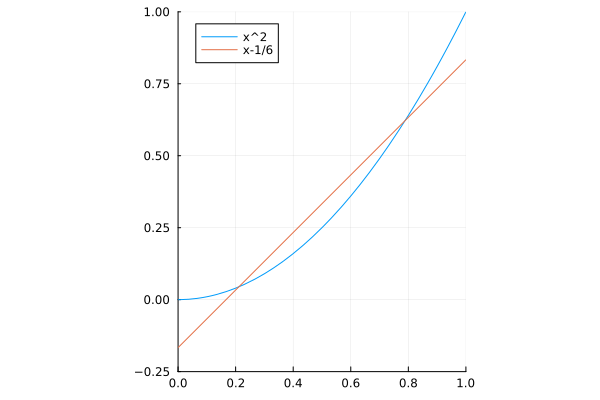
と計算される. $y = x^2$ と $y = x - \frac{1}{6}$ をプロットすると以下のようになり, 区間上で誤差を平均的に小さくするような直線が与えられていそうなことが分かる.
using Plots
plot([x->x^2, x->x-1//6], xlim=(0, 1), ylim=(-1//4, 1), aspect_ratio=:equal, label = ["x^2" "x-1/6"])
savefig("./graph.png")
Julia v1.8.3 (Windows 64bit), Plots v1.38.1 にて出力.
例2 音速の方程式
本記事の元々の動機としては空気中の音速の式が興味の出発点で, 温度$t$ [℃] における$1$気圧の空気中の音速$v$ [m/s]が $v = 20.055 \sqrt{t + 273.15}$ で与えられるらしいので, その直線近似を分析したかった.
適当な点($t=0$ とか$t=15$とか)でテイラー展開を行って1次で打ち切れば直線近似は得られるが, 凸な関数の接線だと「展開点では最良近似だが離れると近似が悪くなる」ため, 興味のある区間中で平均的に良い近似を与える直線を求めたくなり, それで冒頭の命題のステートメントに繋がる.
計算の詳細は省略するが, たとえば $[0, 30]$ [℃]の温度区間での近似を導出すると$v = 0.59 t + 331.5$ くらいになり, リンクのWikipedia 記事中の近似式よりちょっと(最大$0.5$ [m/s]くらい…)近似の良くなる区間が増える.
所感
多分何かしらの本には記載がある話だろうと思いつつ, ちょっと検索した限りではそれらしい話題や用語を見つけられず, 自分で導出してまとめた.
$a, b$ の線形方程式の係数行列は行列式がかなり綺麗に因数分解でき($-\frac{(\beta -\alpha)^4}{12}$), うまいこと出来てるなあと思った.
冷静に考えると, 関数$f$が陽的に与えられている状況で近似直線が欲しくなる状況はあんまり考えにくいかもしれない…
よっぽど計算資源が限られていて, 正確さを犠牲にしてでも$f(x)$の計算負荷を減らしたい, とか？
数学っぽい文章(命題とか)をちゃんと書くのが久々なため, 色々と勘所を忘れている…