1を並べるだけで見える数の神秘～レピュニット数と不思議な性質～

はじめに

$1$ をひたすら並べてみましょう.
1, 11, 111, 1111, 11111, 111111, 11111111, 111111111, 1111111111, …
このように $1$ を $n$ 個並べてできる自然数 $R_n$ は Repunit 数 (レピュニット数) と呼ばれています.¹

高校数学レベルで理解できる内容ですので, 是非肩の力を抜いてお楽しみください！

Repunit数の一般項

数列を与えられるとその一般項を求めたくなるのが全人類の悲しき性です.
なので, まずはRepunit数の一般項を求めていきましょう.
$n$ 番目の Repunit 数を $R_n = \underbrace{1111 \dots 11}_{\text{$n$ 桁}}$ と書くことにします.
このとき $R_n$ は次のように見れば等比数列の和とみなせます.

\begin{align}
R_n &= \underbrace{1111 \dots 11}_{\text{$n$ 桁}} \\
&= 1 + 10 + 100 + \dotsb + \underbrace{1000…00}_{\text{$n$ 桁}} = \sum_{k = 0}^{n - 1}10^k
\end{align}

従って等比数列の和の公式から,

\begin{align}
R_n = \frac{10^n - 1}{9}
\end{align}

となり, 一般項を求めることができました.

Repunit数にまつわる美しい定理

筆者が本記事で一番書きたかった内容です.
Repunit 数について以下に述べる定理が成り立ちます².

$n$ を $2, 5$ を素因数に持たない自然数とする.
このとき, $n$ で割り切れる Repunit 数が必ず存在する.

例えば…
$n$ として $3$ をとると, $3$ で割り切れる Repunit 数として $R_3 = 111$ がとれます.
$n$ として $21$ をとると, $21$ で割り切れる Repunit 数として $R_6 = 111111$ がとれます.
$n$ として $877$ をとると, $877$ で割り切れる Repunit 数として $R_{438} = \underbrace{1111…11}_{\text{438桁}}$ がとれます.

いやあ美しい.
あのシンプルな定義からは想像もできないほどうっとりする定理です.

本章ではこの定理を証明しましょう.
高校数学の美しい物語さんでは Fermat の小定理を用いた証明が掲載されていますが, ここでは別のアプローチを採用してみます.

鳩舎論法

ここでは鳩舎論法について説明します.
主張はとても簡単です.

今, $M$ 羽の鳩がいて $N (< M)$ 個の鳥小屋があるとします.

そして, 鳩達を各鳥小屋に入れていきます.
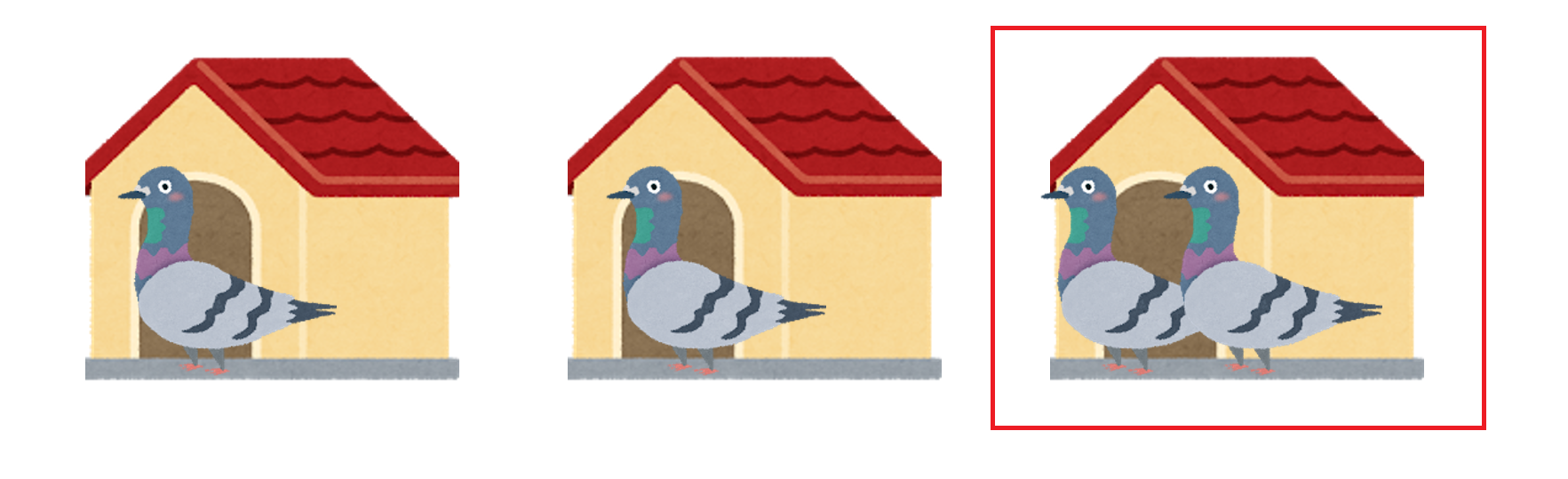
このとき__少なくとも $2$ 羽以上の鳩が入っている鳥小屋が存在する__, というのがステートメントです.

当たり前に感じますが実はとても強力で, 数学の様々な分野でその効果を発揮します.

本記事でもこの鳩舎論法を用いて上述した定理を証明します.

証明

$n$ を $2, 5$ を素因数に持たない自然数とする.
ここで $n + 1$ 個の Repunit 数 $R_1, R_2, …, R_{n}, R_{n + 1}$ を考える.
鳩舎論法より $R_j \equiv R_i\ \ \ (\mathrm{mod}. n)$ となる $1 \leq i < j \leq n + 1$ が存在する.
つまり,

R_j - R_i \equiv 0 \ \ \ (\mathrm{mod}. n) 

である.
このとき,

\begin{align}
R_j - R_i &= \frac{10^j - 1}{9} - \frac{10^i - 1}{9} \\
&= \frac{10^j - 10^i}{9} \\
&= 10^i \cdot \frac{10^{j - i} - 1}{9} \\
&= 10^i R_{j - i}
\end{align}

と計算できるので,

10^i R_{j - i} \equiv 0 \ \ \ (\mathrm{mod}. n)

となる.
今, $n$ は $2, 5$ を素因数に持たないので $10$ と互いに素だから,

R_{j - i} \equiv 0 \ \ \ (\mathrm{mod}. n)

とできる.
従って, $n$ で割り切ることができる Repunit 数 を得ることができた.

(おまけ)コード

コマンドライン引数に数値を渡したときに, その数値で割り切ることができる最小の Repunit 数 を求めるコードを記載しておきます.³

get_repunit_length.py

import sys

def get_repunit_length(number):
    if (number <= 0):
        return -1
    elif ((number % 2 == 0) or (number % 5 == 0)):
        return 0
    else:
        repunit = 1
        length = 0
        while(True):
            length += 1
            if (repunit % number == 0):
                return length
            else:
                repunit = repunit + 10 ** length


if __name__ == "__main__":
    args = sys.argv
    input = int(args[1])

    result = get_repunit_length(input)

    if (result == -1):
        print("自然数を入力してください。")
    elif (result == 0):
        print(f'{input} で割り切れるRepunit数は存在しません。')
    else:
        print(f'{input} で割り切れる最小のRepunit数は R_{result} です。')

Repunit素数

ここからはおまけです.

Repunit 数でありかつ素数であるものを Repunit 素数 といいます.
例えば $R_2 = 11$ は Repunit 素数 です.
また $R_{19} = 1111111111111111111$ も Repunit 素数です.
他に Repunit 素数 にはどのようなものがあるでしょうか？
Wikipediaには以下の表が掲載されています.
ここで, $n$ というのは $n$ 番目の Repunit 数 を意味しています.

$n$	発見年	発見者
$2$	-	-
$19$	-	-
$23$	-	-
$317$	1978	Williams
$1031$	1986	Williams, Dubner
$49081$	1999	Dubner
$86453$	2000	Baxter
$109297$	2007	Dubner
$270343$	2007	Voznyy

現在分かっている Repunit 素数 はこの $9$ つだけです.
Repunit 素数が無数にあるかどうかは未解決問題となっています.

いつ Repunit 数が素数になるかはわかっていませんが, 部分的に調べることもできます.
例えば, $n$ が合成数のときは $R_n$ も合成数となります.⁴

自然数 $n, m$ に対して, $m$ が $n$ を割り切るのであれば $R_m$ は $R_n$ を割り切る.

上記性質の証明は是非皆さんも考えてみてください.
一応ここにも書いておきますので, 答え合わせにどうぞ.

証明

$m$ は $n$ を割り切るので, ある自然数 $k$ を用いて $n = km$ とかける. このとき,

\begin{align}
R_{n} &= \frac{10^n - 1}{9} \\
&= \frac{10^{km} - 1}{9} \\
&= \frac{(10^m)^k - 1}{9} \\
&= \frac{(10^m - 1)(10^{m(k - 1)} + 10^{m(k - 2)} + \cdots + 1)}{9} \\
&= (10^{m(k - 1)} + 10^{m(k - 2)} + \cdots + 1)R_{m}
\end{align}

となり, $(10^{m(k - 1)} + 10^{m(k - 2)} + \cdots + 1)$ は自然数だから $R_m$ は $R_n$ を割り切る.

おわりに

数学って本当に面白いんですよ.
もちろんゴリゴリの解析学や代数学, 位相数学を駆使して挑むような分野であったり, 問題設定自体がかなり高度なものがほとんどです.
けどそれだけじゃない.
例えば今回みたいに適当に数を並べたり, 数を入れ替えたりしてみるだけでもそこには華々しい珠玉の数学達が眠っています.⁵

1. Repunitという名前の由来は「Repeated(繰り返す)」 + 「Unit(1)」からきています
   つまり,
   $R_1 = 1$,
   $R_2 = 11$,
   $R_3 = 111$,
   $R_4 = 1111$,
   $R_5 = 11111$,
   ………
   といった具合です.
   とてもシンプルな定義の Repunit 数ですが, 実はいくつかの不思議な性質を持っています.
   本記事ではその性質達について紐解いていきましょう. ↩

2. AtCoder ABC174 C.Repsept ではこの定理が背景にある問題が出題されています
   問題名は Repsept で, これは「Repeated(繰り返す)」 + 「sept(7)」からきているようですね ↩

3. このコードを $777…77$ 用に修正してもAtCoder ABC174 C.Repseptでは TLE となり通りません
   もう一工夫が必要となります ↩

4. $n$ が素数のときに $R_n$ が素数になるとは主張していないので注意してください
   これは, Repunit 数に関する次の性質から直ちに分かります. ↩

5. 三角関数に隠された組み合わせの秘密でも数をジグザグ並べただけでしたよね (宣伝)
   これってすごいことだと思うんです.
   たまには数遊びでもしてみて, あなただけの数学と戯れてみるのもいいのではないでしょうか。
   もし面白そうなテーマや発見があったら是非教えてください！ ↩