『非平衡統計力学 基本法則から読み解く物理学最前線』(沙川, 2022) 第2章を参考に、非平衡での熱力学的法則をまとめる。
一部の式番号は文献と一致させている。
ゆらぐ熱力学系 と 熱力学第1法則の微分形
先に非平衡な状態を一般に定義してから、その特殊な状態として平衡状態（普通の統計力学）を求める
（これは文献と逆順の説明方法だがその方がわかりやすかった）
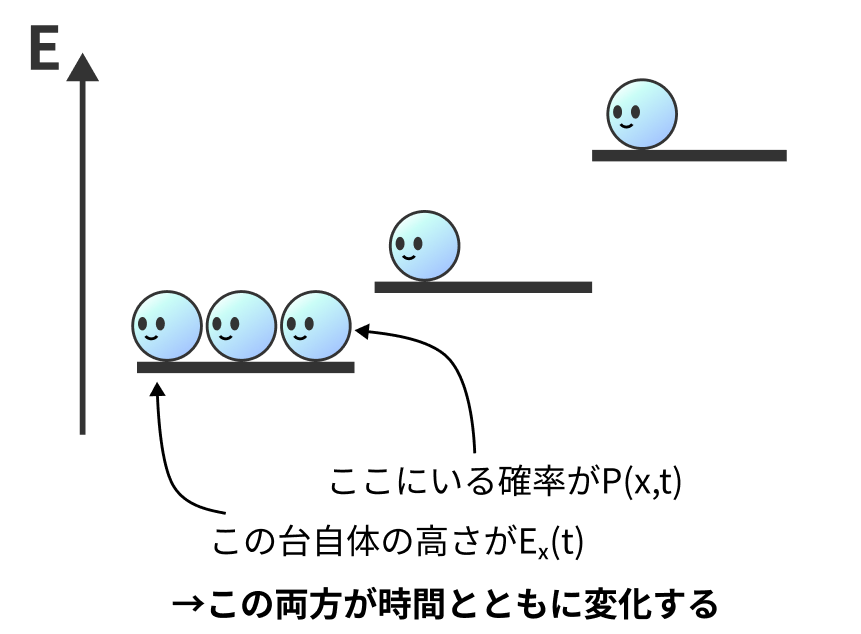
システム$X$の取りうる状態を$x$とする。
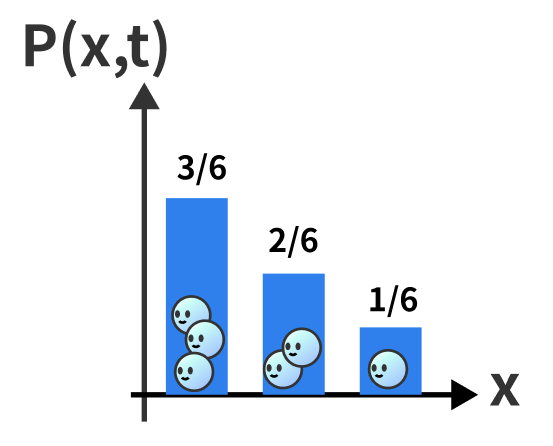
それらの確率を$P(x,t)$とする（時間発展するので時間tへの依存性がある）。
状態が$x$の時のエネルギーを$E_x$とする。
各エネルギー$E_x$が時間によって変わる場合、$E_x(t)$と書いておく。
平均エネルギー$E(t)$は、
$$ E(t) := \sum_x P(x,t) E_x(t) $$
と定義される。
$P(x,t)$と$E_x(t)$が両方動くというのが最初はイメージしづらかったが、下図のように考えると良い。
粒子がそれぞれのエネルギーの高さ$E_x$を持つ状態$x$の台の上にいると考える。
その状態$x$にいる確率が$P(x,t)$。その台の高さが$E_x(t)$。
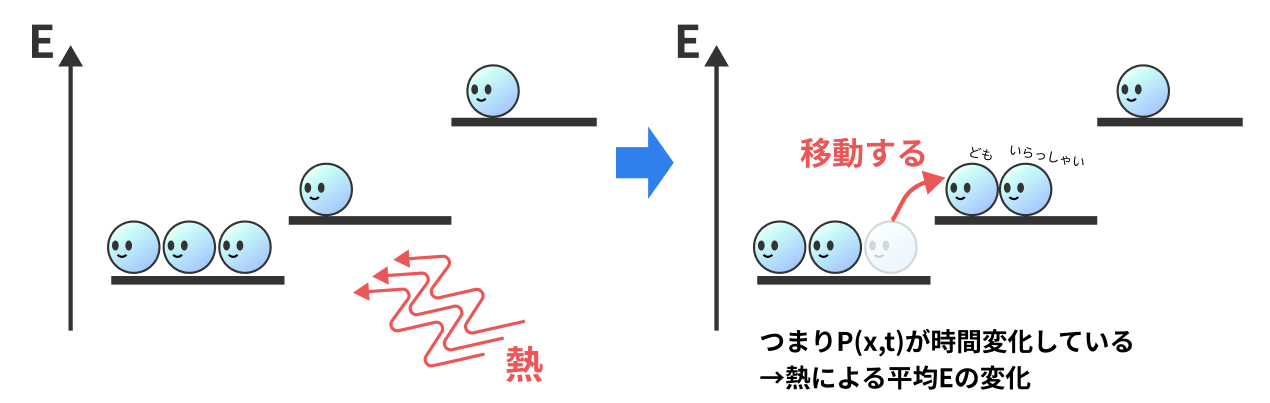
ケース1：仕事を与えずに、熱を与える場合
時刻τからtまでの間に吸収した熱量Q(τ)は、
$$Q(τ) = E(τ)-E(0) = \sum_x(P(x,τ)-P(x,0))E_x$$
時間微分をすると、
$$\dot{Q}(t)=\frac{dE(t)}{dt} = \sum_x \frac{∂P(x,t)}{∂t}E_x$$
熱浴からの熱によって、$P(x,t)$が変化して、平均$E$が変わる。
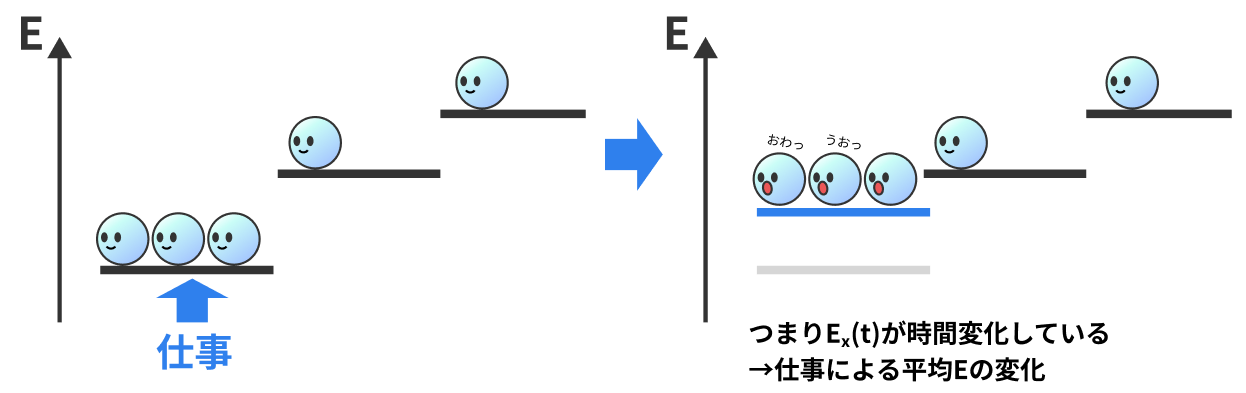
ケース2：熱を与えずに、仕事を与える場合
時刻$t$に、エネルギー準位自体の高さを$E_x$から$E_x'$に瞬間的に変える。
瞬間的な変化の場合は、熱の吸収はゼロとみなせる。
仕事がエネルギー変化と一致する。
$$W = \sum_x P(x,t)(E_x' - E_x)$$
$E_x(t)$の高さ自体を一瞬で変えることで（クエンチ）、平均$E$が変わる
一般化してWとQが変わる場合
平均エネルギーの式
$$ E(t) := \sum_x P(x,t) E_x(t) $$
を時間微分すると、
$$\frac{dE(t)}{dt} = \sum_x \frac{∂P(x,t)}{∂t} E_x(t) + \sum_x P(x,t) \frac{∂E_x(t)}{∂t}$$
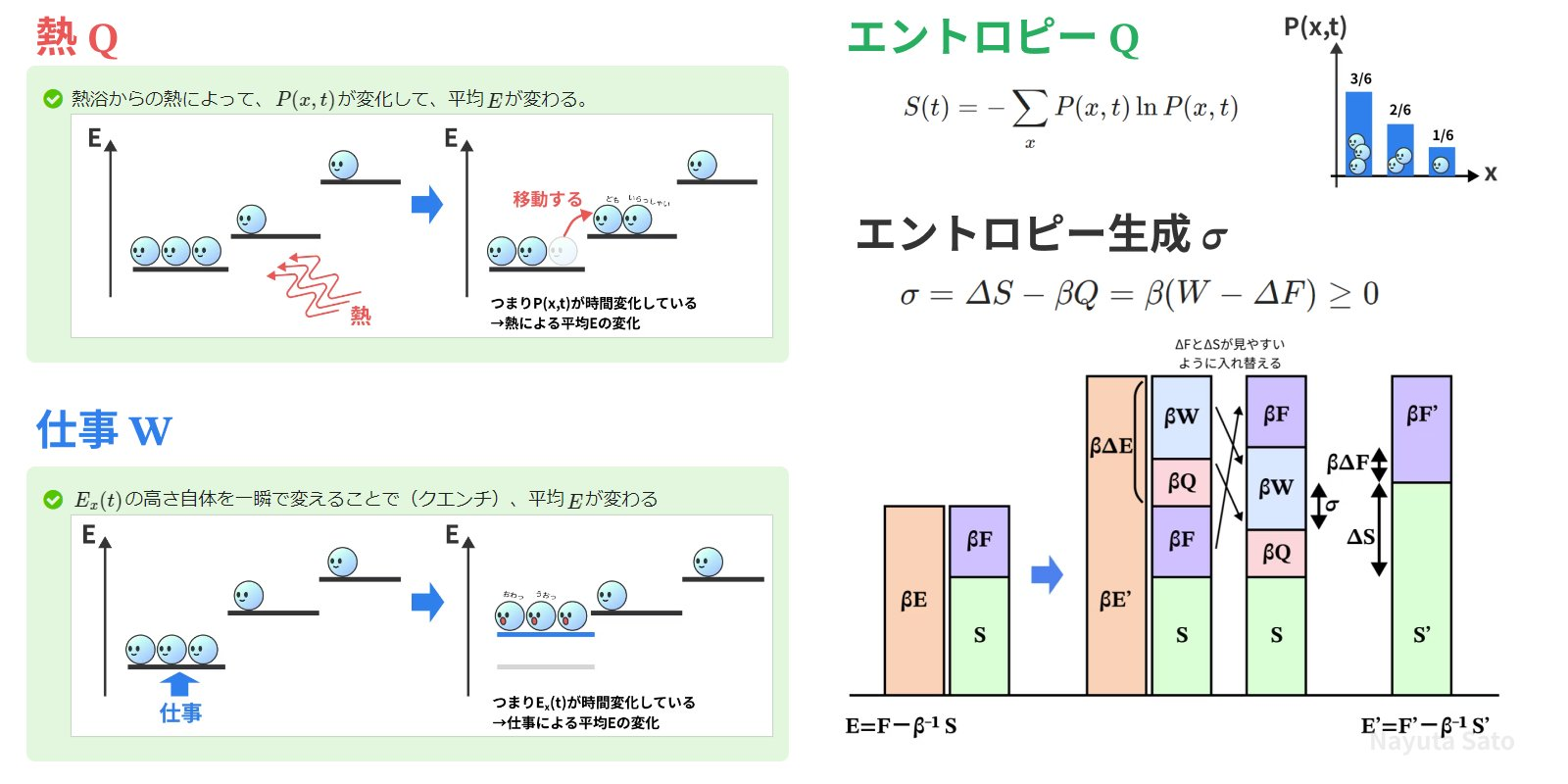
この第1項は、熱浴の影響でxが変動することによるエネルギーの変化なので、熱である。
$$\dot{Q}(t) = \sum_x \frac{∂P(x,t)}{∂t} E_x(t)$$
第2項は、エネルギー準位自体の変化によるエネルギーの変化なので、仕事である。
$$\dot{W}(t) = \sum_x P(x,t) \frac{∂E_x(t)}{∂t}$$
よって、
$$\frac{dE(t)}{dt} = \dot{Q}(t) + \dot{W}(t)$$
これは熱力学第1法則の微分形になっている。
エントロピー
エントロピーは、一般の分布に対して、シャノン・エントロピーとして定義できる。
$$S(t) = -\sum_x P(x,t) \ln P(x,t)$$
例えばこのような確率分布であれば、
$S(t) = -\frac{3}{6}\ln(\frac{3}{6}) - \frac{2}{6}\ln(\frac{2}{6}) - \frac{1}{6}\ln(\frac{1}{6})≒1.01$
となる。
エントロピーSは、一様分布に近いほど大きくなる。
例えば、[1/3,1/3,1/3]という分布なら、$S=1.10$
一方、あるxだけが突出して他が0の分布ほど小さくなる。
例えば、[1,0,0]という分布なら、$S=0$となる。
（※$\lim_{p→0} p \ln p = 0$ を使った）
$P(x,t)$についてすべての$t$について$\sum_x P(x,t) = 1$であることから、
$$\sum_x \frac{∂P(x,t)}{∂t} = 0$$
これを使って、エントロピーSの時間微分は、
$$\frac{dS(t)}{dt} = - \sum_x \frac{∂P(x,t)}{∂t} \ln P(x,t)$$
となる。
平衡系の場合
特殊な場合として、平衡系の場合を考える。
（その場合だけを考えればよくて時間依存は考えなくてよいので$t$をなくしている）
エネルギー期待値は、
$$E=\sum_x P(x)E_x$$
このエネルギー準位の下での平衡分布は、カノニカル分布で与えられる。
$$P_{can}(x) = \frac{e^{-βE_x}}{\sum_x e^{-βE_x}}$$
見覚えがある形だが、これは機械学習でよく使うsoftmaxと同じ形。高い$E_x$を持つ状態ほど確率が低いような分布になっている。
分母は規格化定数で、すべての$x$について確率の和を取ったときに1になるようにするためのもの。分布の形は分子によって決まっている。
分母を分配関数$Z = \sum_x e^{-βE_x}$と置くと、
$$P_{can}(x) = \frac{e^{-βE_x}}{Z}$$
平衡自由エネルギーは、
$$F_{eq} = -k_B T \ln Z = -β \ln Z$$
と定義される。
カノニカル分布は、$F_{eq}$を使って書き直すと、
$$P_{can} (x) = e^{β(F_{eq} - E_x)}$$
イメージのしかた：
平均エネルギーが$E$となるように、各$E_x$の大きさに沿って、$E_x$が低いほど確率が多く、高いほど確率が低くなるように、完全に粒子の分布が定まったとき平衡状態に達して、カノニカル分布になる。
カノニカル分布以外はすべて非平衡状態である。
エントロピーは、前述の通り、$S = -\sum_x P(x) \ln P(x)$で求まる。
（ここでいうエントロピーは一般の分布に定義できる情報理論的なシャノン・エントロピー。まだカノニカル分布のシャノン・エントロピーが熱力学のエントロピーと同じかどうかは言えていないが、一致することをここで示す。）
$P_{can}$をSの式に代入すると、
$$\begin{align}
S &= -\sum_x P(x)β(F_{eq} - E_x) = β(E-F_{eq}) \\
E &= F_{eq} + k_B TS
\end{align}$$
これは平衡熱力学エントロピーが満たす関係式（$F_{eq} = E-k_b TS_{eq}$）と同じになっていて、そのことから、カノニカル分布では$S = S_{eq}$となる。
カノニカル分布のエントロピー$S_{eq}$は、平均エネルギーが$E$となる分布の中で最大のエントロピー$S$を持つ（証明略）。
ここまでで、非平衡状態を一般の場合として定義し、その特殊な状態として平衡状態を定義した。
まだ定義していないものとして、平衡状態の$F_{eq}$に対応する一般の非平衡な$F$が何なのかが残っている。
熱力学第二法則
まず平衡状態の熱力学第二法則から出発する。
クラウジウスの不等式：
$$ΔS_{eq} - βQ ≥ 0 \tag{2.23}$$
（Qは吸収した熱量、βは熱浴の逆温度）
いわゆるエントロピー増大則は、断熱過程で$Q=0$の時には$ΔS_{eq} - βQ ≥ 0$ となることを言っている。
断熱過程でなければ、Qを負にすればエントロピーは増やせる。
これを非平衡に置き換えた式も多くの系で普遍的に成り立つことが示せる（証明略1）。
非平衡の熱力学第二法則
$$ΔS - βQ ≥ 0 \tag{2.25}$$
式(2.25)の左辺をエントロピー生成
$$σ=ΔS - βQ \tag{2.26}$$
と定義する。
（これは系のエントロピー変化$ΔS$と、熱浴のエントロピー変化$-βQ$の和になっている。）
熱力学第二法則は、「エントロピー生成が非負」と言い換えられる。
非平衡自由エネルギーを
$$F = E-β^{-1}S$$
と定義する。平衡自由エネルギー$F_{eq} = E-k_b TS_{eq}$をそのままの形で非平衡の$S$（シャノンエントロピー）に置き換えたものになっている。
(2.26)から変形する。
$$\begin{align}
σ &= ΔS - βQ \quad = Δ(βE-βF) - βQ \\
&= βΔE-βΔF - βQ \quad = β(W+Q) - βΔF - βQ \\
&= β(W-ΔF) \\
&≥0
\end{align}$$
よって、
$$W≥ΔF \tag{2.29}$$
これはクラウジウスの不等式の別の表現になっている。
された仕事が、自由エネルギー変化量の上限であることを示している。
（※逆に$W_{out} = -W ≤ ΔF$ であるから、取り出せる仕事の上限は自由エネルギー変化量で決まることがわかる。）
カノニカル分布での$F = E-β^{-1}S$は、$F_{eq}$に一致する（←そう定義した）。
また、一般の非平衡分布の中で最もFが小さいものがカノニカル分布であり、
$$F≥F_{eq}$$
となる（証明略）。
エネルギーの変化を図で理解する
（この章は記事筆者の補足）
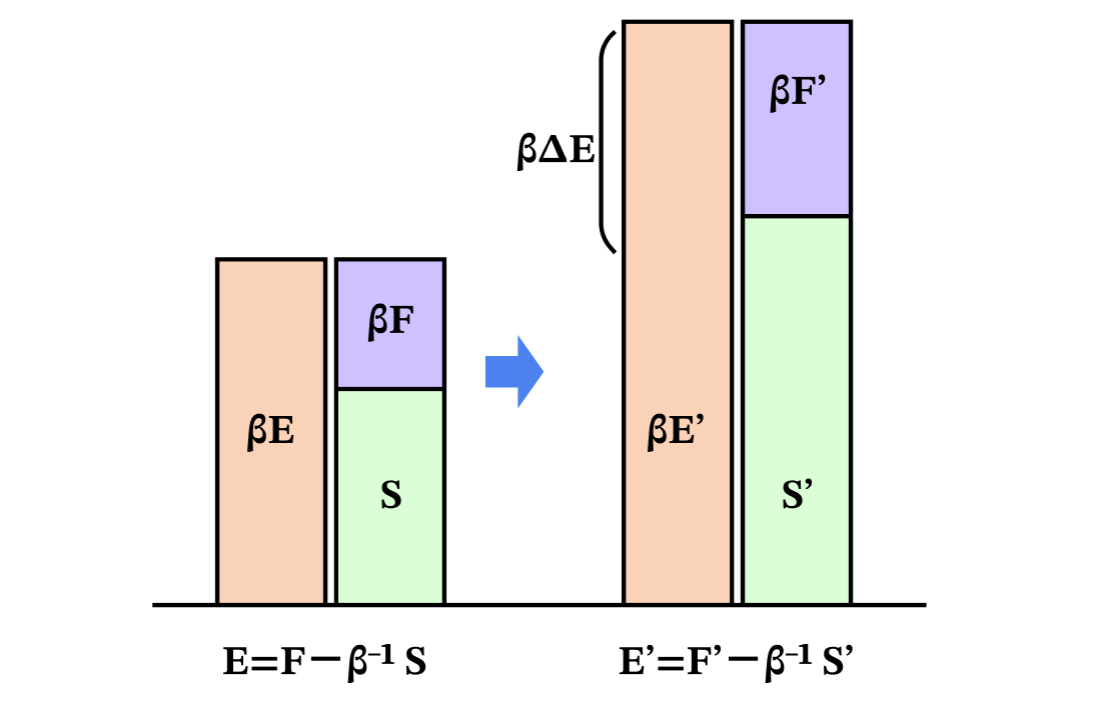
非平衡状態でも$E$, $S$は定義できて、それらから非平衡自由エネルギー$F=E-β^{-1}S$ が求まる。
両辺にβをかけて整理すると、$βE = S + βF$ である。
今ある非平衡状態（$E,S,F$）から別の非平衡状態（$E',S',F'$）に移ったとする。
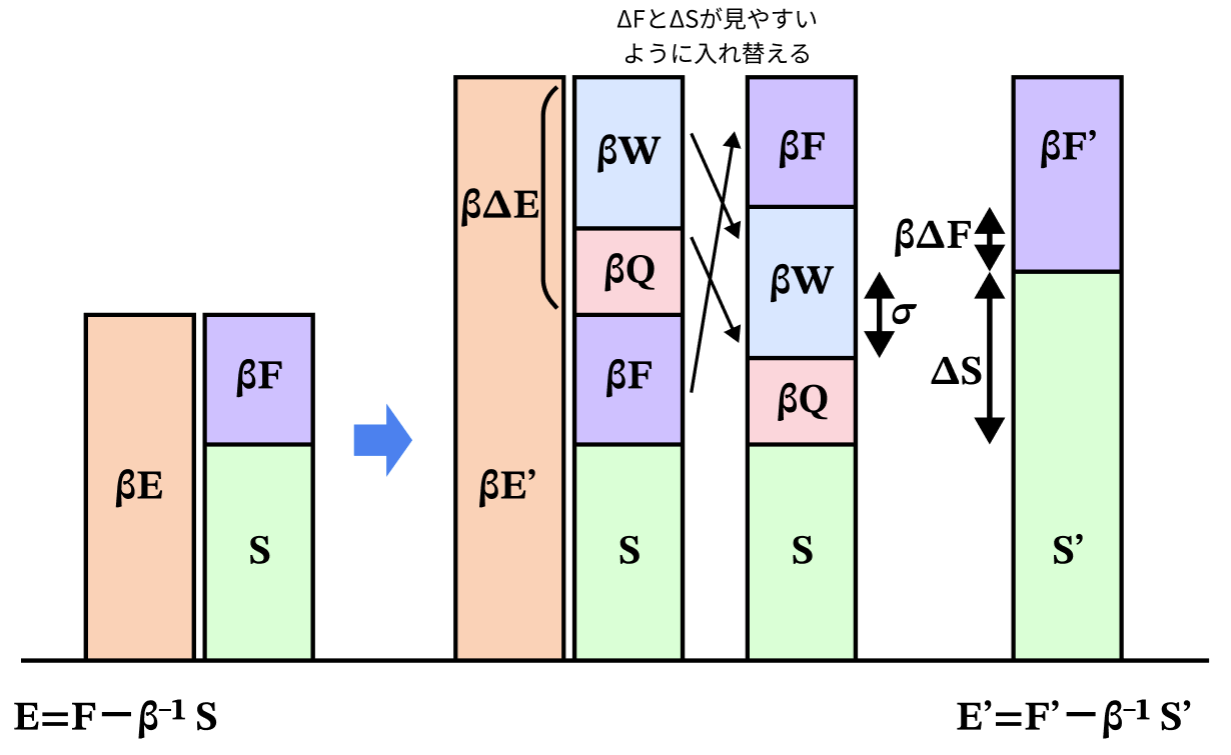
この図の中に、さらに$Q$と$W$を書き込んでいく。
エネルギーの増加分は$ΔE=W+Q$であるので、これを$β$倍して図に書き込む。
$ΔF$と$ΔS$が見やすいように順番を入れ替えると、図の中にエントロピー生成$σ$が出てくる。
（※復習：エントロピー生成は$σ = ΔS - βQ = β(W-ΔF) ≥0$なる量だった）
今までに登場したものがこの図の中にきれいに整理できる。
外から与えられた仕事$W$と熱$Q$は、$F'$と$S'$の一部に変わっていく、といえる。
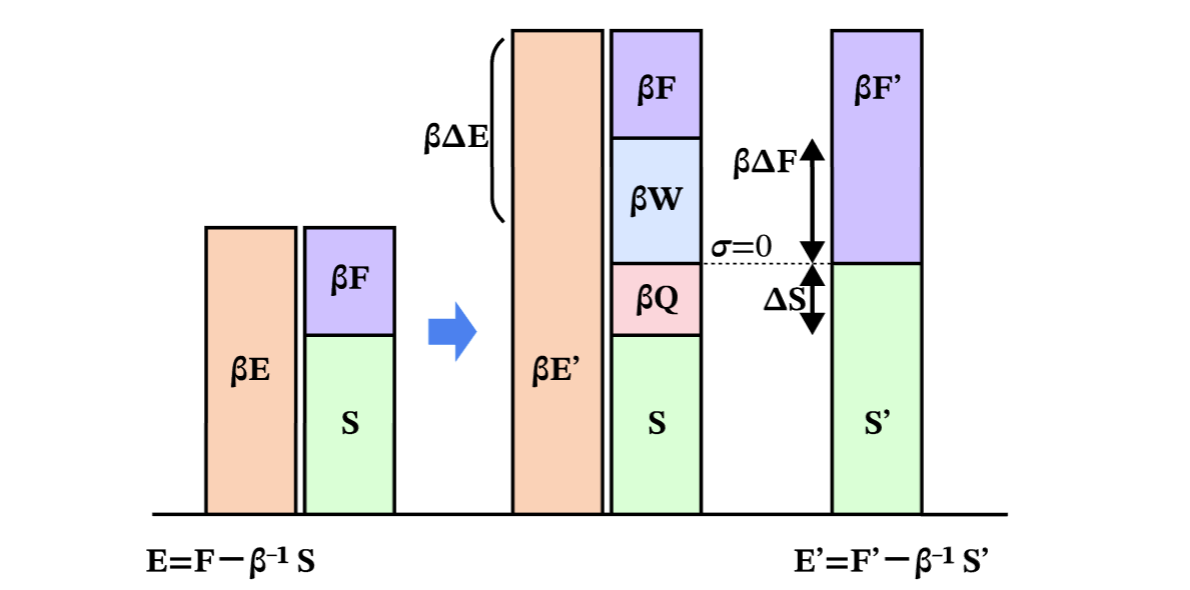
さて、$σ≥0$ だったが、この等号成立の時にはどうなるか？
上の図にある$σ$の幅がぎゅーっと押しつぶされて0になったとき図は下のようになる。
（等号が成立するときは、準静的過程のときであり、系がずっと熱平衡状態にある場合。2）
仕事$W$と熱$Q$の和は、一般に$F'$と$S'$の一部に変わっていくが、特別に統合成立の場合（準静的過程で熱平衡を保った場合）のみ
外から与えた仕事$W$が全て自由エネルギーの増分$ΔF$になり、
外から与えた熱$Q$が全てエントロピーの増分$ΔS$になるような過程となる。
（筆者はこの図を描いて、今までのわからなさがすーっきりと解決したので、理解の助けになれば幸いです。）
まとめ図
おまけ：記事筆者の展望
予測符号化を行うニューロン群の系に対して、非平衡統計力学的なマクロ量（$F,E,S,Q,W$）を計算して、その時間発展をモデル化しようとしている。
ニューロン群によって作る分布$q$の形を変えながら、正解の分布$p$に近づけていく。
この時、分布$q$の形を変えることは、確率分布自体の変化なので、$\dot{Q}$の式に相当する。つまり熱の単位時間変化。
また、正解の分布$p$が瞬時に変わることは、クエンチをすることに相当する。つまり仕事$W$。
エネルギーベースモデルで考えれば、エネルギーを変数で微分した値に応じて分布が変わる。つまり、分布$q$の変化（ひいては熱の変化）を陽に記述できる。
※エネルギーベースモデルの例（Modern Hopfield Model）
https://amhn.vizhub.ai/demo/
エントロピー$S$は予測分布$q$のシャノン・エントロピーであり、これも分布から求められる。
正解の分布$p$が変わった瞬間に一瞬で$W$が入り、エネルギーが増加する。
その後、予測分布$q$の形を変えることで緩やかにエネルギーを下げていく（この時、$Q$の排出と$S$の増減が起こる）。
これを使って、音楽に対する予測を連続時間ステップで生み出すモデルを作り、それに対する自由エネルギー$F$の変化を連続時間で検討しているところ。
このあたりに詳しい方いらしたらコメントくださいませ🙇