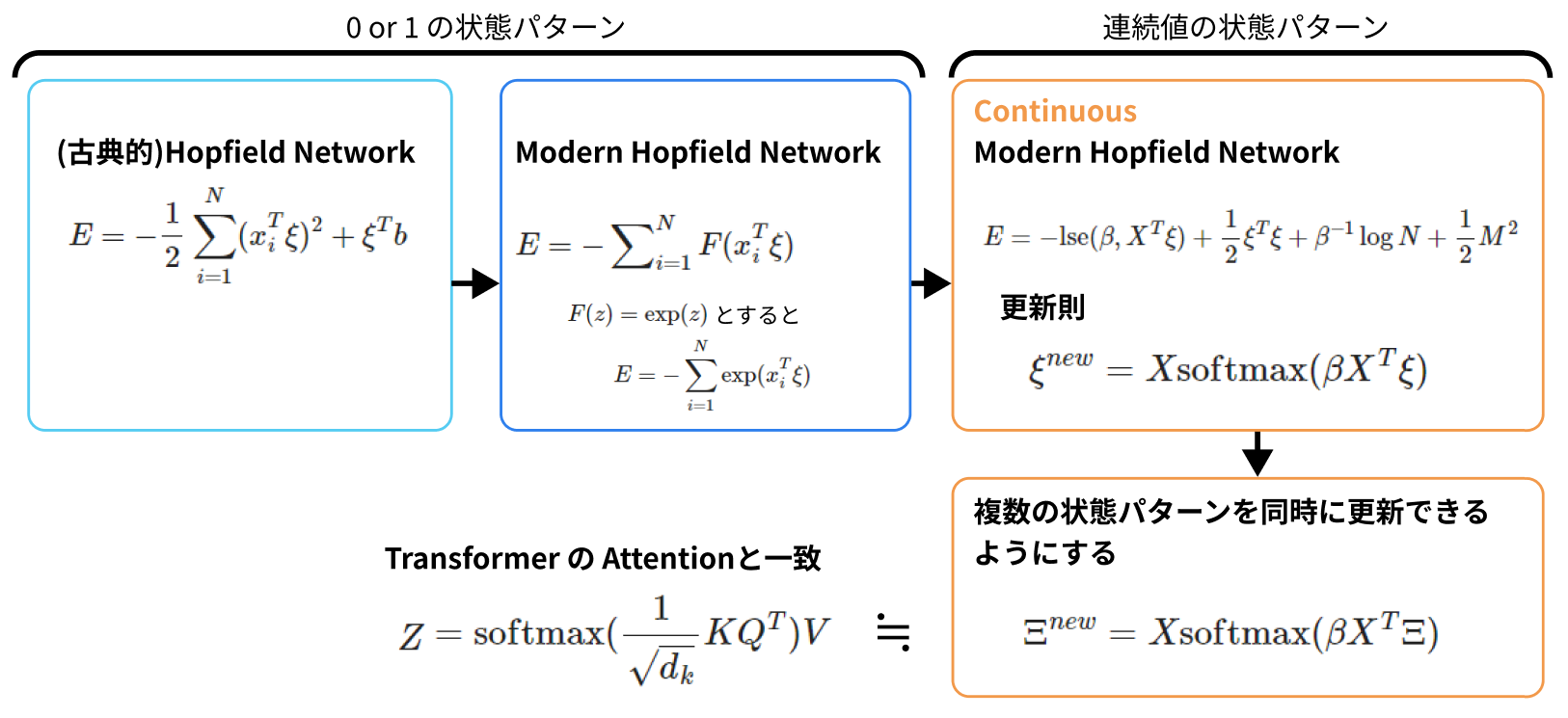
本記事では、下記リンクの記事の解説を行う。
"Hopfield Networks is All You Need"
https://ml-jku.github.io/hopfield-layers/ 1
※なお、本記事は解説を目的としたもののため、原文に忠実な翻訳ではない。
記事の解説
かんたんな説明
Q. 何を実現するためのネットワーク?
→ネットワークにパターンを覚えこませて、入力したものを連想記憶的に引き出すことができる。
例えば、10枚の絵を覚えさせて、今画像の一部分だけをネットワークに入力したときに、元はどの絵だったのかを復元することができる。
Q. 何がうれしいかというと?
→1ステップの演算で結果が収束し、連想記憶が引き出せる。
Transformerのattentionとの関連性が示されていて、ニューラルネットワークの1レイヤーとしても導入できる。
連続値に拡張したModern Hopfield Networkでは、指数関数的な容量を持つことができ、復元精度も高くなる。
この記事では、Transformerのattentionの計算とModern Hopfield Networkの計算が一致することを示す。
章立て
- (古典的)Hopfield Networkの基礎
- 拡張その1:Modern Hopfield Network
- 拡張その2:連続値のパターン・状態
- 拡張その3:複数の状態パターンへの拡張 →self-attentionになる
という順番で拡張を進めていく。重要なのは「3.拡張その2」。
最初に離散的な2値状態を取るモデルから始めて(1節)、次にエネルギー関数を改良して容量の拡張を行い(2節)、さらに連続値の状態を取れるように拡張する(3節)。
そして、状態パターン(入力に該当する)を複数入れて一気に更新するように拡張を行う(4節)。これはTransformerに使われるself-attention機構と同じものになることを示す。
1.(古典的)Hopfield Networkの基礎
※この章は、「単純な2値モデルを作ってもうまくいかないね」という話なので読み飛ばして後から戻ってきてもよい。後に拡張のために使うので詳細に書いている。
| ネットワーク | 値 | 容量 | 更新則 |
|---|---|---|---|
| (古典的)Hopfield Network | 2値(+1か-1) | 0.14d | ヘブ則 |
直積 (outer product) で定義される最もシンプルな連想記憶モデル。
N個のパターン $\lbrace x_i \rbrace (i=1,...,N)$ を記憶させることができる。
それぞれの値は、$ x_i∈ \lbrace −1,1 \rbrace ^d$ のように正負の2値を持つ。 (d次縦ベクトル)
それぞれが全結合するので、重み行列は、
$$ W = \sum_i^N x_i x_i^T $$
となる。
状態パターン (state pattern) $ξ$ から始めて検索されるパターンを、この重み行列は保存することができる。
基本的な同期更新則 (synchronuous update rule) は、次のような更新式。
$$ ξ^{t+1}=\mathrm{sgn} (Wξ^t−b) \tag{2}$$
sgnは符号。bはバイアス項であり、各コンポーネントの閾値として解釈できる。
つまり、各コンポーネントについて、重み$W$を$ξ^t$にかけたものが$b$を超えたかどうかを判断して、その値を次の状態にするということになる。
非同期的更新則 (asynchronous update rule)は、$ξ$ のある1つのコンポーネントについて次のコンポーネントを選択して更新する。
$ξ^{t+1}=ξ^t$ の時に収束する。
この非同期的バージョンの更新則(2)は、エネルギー関数Eを最小化する。
$$
\begin{align}
E&=−\frac{1}{2}ξ^TWξ+ξ^Tb \\
&=−\frac{1}{2}∑_{i=1}^d ∑_{j=1}^d w_{ij}ξ_iξ_j+∑_{i=1}^d b_iξ_i \tag{3}
\end{align}
$$
導出の補足
やっていることは、$x_iξ$の2乗を取るような処理だ。
$$\begin{align}
ξ^TWξ &= ξ^T x_i x_i^T ξ \\
&= \sum_{i=1}^N (x_i^T ξ)^T (x_i^T ξ) \\
&= \sum_{i=1}^N (x_i^T ξ)^2
\end{align}
$$
ということだ。
つまり、
$$ E = -\frac{1}{2} \sum_{i=1}^N (x_i^T ξ)^2 + ξ^T b$$
という形だと言える。
後で出てくるDiscrete Hopfield Networkモデルはこの「2乗」の部分を、$(x_i^T ξ)^a$や、$\exp(x_i^T ξ)$に拡張したものだということが後から分かる。
(補足ここまで)
同期的・非同期的更新則ともに、$E(ξ^{t+1})≤E(ξ^t)$は満たされる。そして、$E(ξ^{t+1})=E(ξ^t)$ となった時に、$ξ^t$は$E$の局所最小値に達する。
全てのパターン $\lbrace x_i \rbrace$ はHopfield Networkのfixed pointにある。つまり、
$$ x_i = \mathrm{sgn} (Wx_i - b)$$
このモデルでは、記憶容量$C$の限界が
$$C \cong \frac{d}{2\log(d)}$$
となっている。
エラー割合を小さく検索できる容量の限界は、
$$C \cong 0.14 d$$
とされている。
この結果を見ると、パターンが適切に検索できていない。このモデルでは精度が出ず容量も小さいので、類似しているパターンを区別できるように「類似したものを引き離す」ようなモデルが必要となる。
拡張その1:Modern Hopfield Network
| ネットワーク | 値 | 容量 | 更新則 |
|---|---|---|---|
| Discrete Modern Hopfield Network | 2値(+1か-1) | $α_ad^{a−1}$ | エネルギー差による符号反転(式(16)) |
$$E=−∑_{i=1}^N F(x_i^T ξ) \tag{9}$$
Fは相互作用の関数。Krotov & Hopfield (2016) では、$F(z)=z^α$としている。
このモデルだと、小さい誤差割合に押さえられるパターン容量は$α_ad^{a−1}$に増える($α_a$はエラー確率のスレッショルド)。
ここで$a=2$とすると、古典的Hopfield modelになる。
$F(z)$には別の関数を取ることもでき、$F(z)=\exp(z)$を取るモデルも作れる(Demircigil et al.)。
| ネットワーク | 値 | 容量 | 更新則 |
|---|---|---|---|
| Model in Demircigil et al. | 2値(+1か-1) | $$2^{\frac{d}{2}}$$ | エネルギー差による符号反転(式(16)) |
$F(z)=\exp(z)$ を取る場合には、エネルギー関数は、
$$ E= - \sum_{i=1}^N \exp (x_i^T ξ) \tag{12}$$
となる。log-sum-exp 関数 (lse) を導入して適用すると、
$$ E= - \exp(\mathrm{lse} (1, X^T ξ)) \tag{13}$$
$$
\mathrm{lse} (β, z) = β^{-1} \log (\sum_{l=1}^N \exp(βz_l)) \tag{14}
$$
と書き直せる。
※ここではlseの1項目が1なので効果が薄いが、後から一般の逆温度βに拡張するので、その時に効果が分かる。
ここから式(9)と(12)ともに有効な更新則を見ていく。
ξは-1 or 1を持つd次元のベクトルであり、この$l$番目を$ξ[l]$と表すことにする。
更新後のξは、今のエネルギーと、$l$番目の値$ξ[l]$の符号を反転させたときのエネルギーとの差で表される。
$$ ξ^{new}[l]=\mathrm{sgn} [−E (ξ^{(l+)}) + E(ξ^{(l−)})] \tag{16}$$
sgnは符号関数であり、その中身の値が正か負かによって-1 or 1を取る(中身が0の時は0になる)。
古典的Hopfield Networkとは異なり、modern Hopfield Networkは、重みの行列を持たない。その代わりに、式(9)や式(12)のように、保存されたパターン$x_i$ と状態パターン $ξ$の内積の関数の和を、エネルギー関数として持つ。
このモデルを使った実験。ちゃんと検索できている。24パターンに増やしてもできている。

古典的Hopfield Networkと比べて、容量が増えたことで、似た(強く相関する)パターンを区別することができるようになり、1つのパターンを検索することができるようになった。
拡張その2:連続値のパターン・状態
| ネットワーク | 値 | 容量 | 更新則 |
|---|---|---|---|
| Continuous Modern Hopfield Network | 連続値 | (指数的な容量) | $$X \mathrm{softmax} (βX^Tξ)$$ |
これを連続値に拡張する。式(13)から出発する。
$$ E= - \exp(\mathrm{lse} (1, X^T ξ)) \tag{13}$$
式(13)の負のエネルギーの対数と、2次の項を入れる($ξ$が有限になるようにするため)。
$$ E=− \mathrm{lse} (β,X^T ξ)+ \frac{1}{2}ξ^Tξ+β^{−1} \log N+\frac{1}{2}M^2 \tag{18}$$
N:パターンの個数、Mはパターンの最大のノルム。
ここから導出していく。
Eの凸項(convex)と凹項(concave)に分ける。
凸項$E_1(ξ)$ は $\frac{1}{2}ξ^T ξ + C$
凹項$E_2(ξ)$ は $-lse(β,X^Tξ)$
$$\begin{align}
∇_ξE_1(ξ^{t+1}) &= −∇_ξE_2(ξ^t) \\
∇_ξ(\frac{1}{2}ξ^Tξ+C)(ξ^{t+1})&=∇_ξ \mathrm {lse}(β,X^Tξ^t) \\
ξ^{t+1} &= X \mathrm{softmax} (β X^T ξ^t) \tag{21}
\end{align}
$$
よって、更新式はこうなる。
$$ ξ^{new} = X \mathrm{softmax} (βX^Tξ) \tag{22}$$
(補足)ここで、lseの微分をsoftmaxに変えるところがやや難しいので解説を補う。
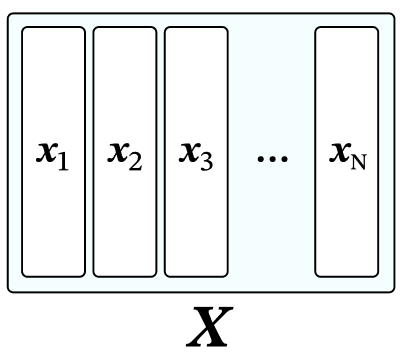
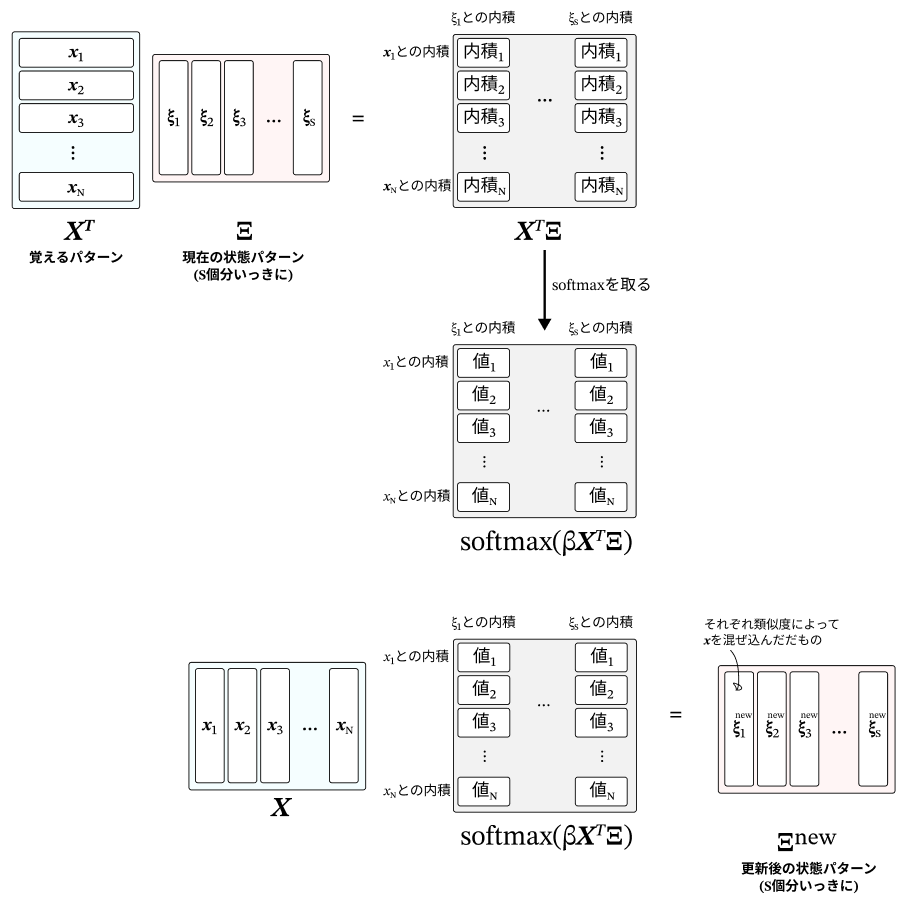
$X^T ξ$は下図のようにそれぞれの$x_i$と$ξ$の内積を縦に並べた縦ベクトルの形になる。
$$\begin{align}
∇_ξ \mathrm{lse}(β,X^Tξ)
&= ∇_ξ β^{-1} \log (\sum_{l=1}^N \exp(β X^Tξ_{[l成分]})) \\
&= β^{-1} (\frac{∂}{∂ξ}β X^Tξ)
\frac{\exp(β X^Tξ)}{\sum_{l=1}^N \exp(β X^Tξ_{[l成分]}) }\\
&= β^{-1} β X \frac{\exp(β X^Tξ)}{\sum_{l=1}^N \exp(β X^Tξ_{[l成分]}) }
\\
&= X \mathrm{softmax}(βX^Tξ)
\end{align}
$$
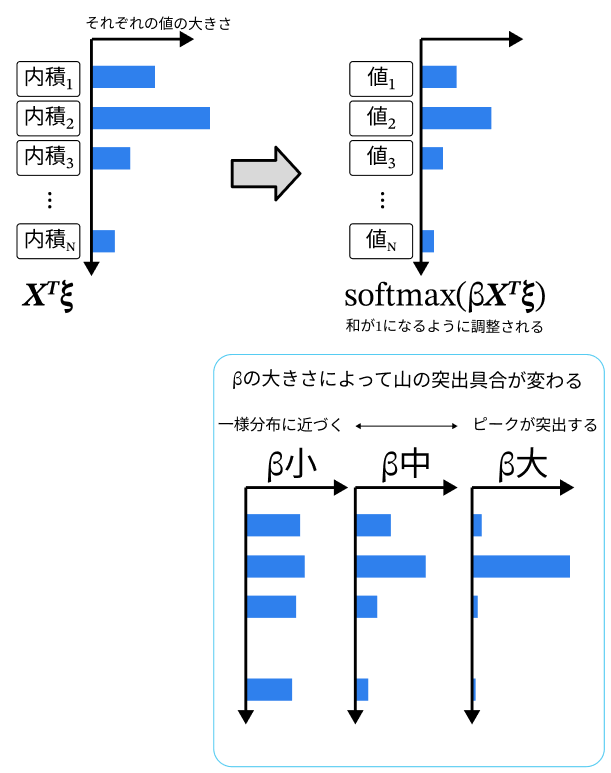
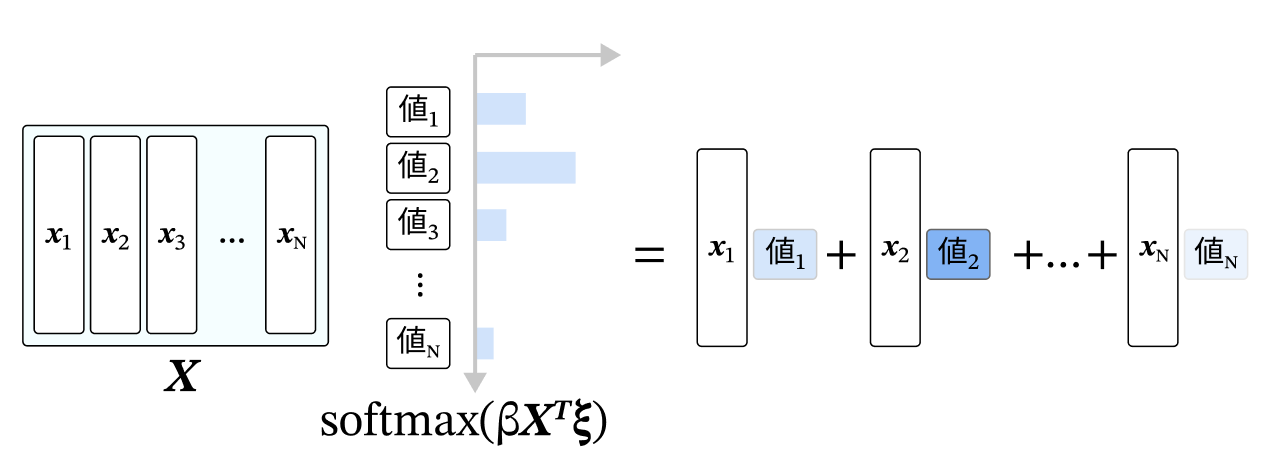
softmaxの中身は、覚えさせたいパターンと、現在の状態の内積(に逆温度βをかけたもの)なので、
この値は類似度を表すことになる。
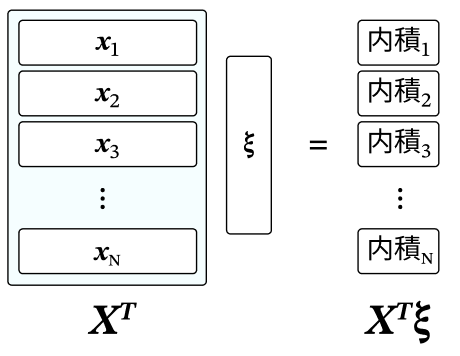
Xとこのsoftmax値との積を取ると考えると、今の状態と類似しているものをたくさん混ぜ込んで、類似していないものを少なく混ぜ込むという操作をしていることになる(下図)。
(※類似度については、原文にない筆者の補足)
与えた顔上半分の状態パターン(state pattern)から連想させる実験を行うと、このように画像を混合したものが得られる。
$β$の値を大きくしていくと、類似度のピーク値のものをほぼ1で混ぜ込み、他をほぼ0で混ぜ込むようになっていく。そのため、最も似ているパターンが優勢となって検索されるようになる。
下図は$β$を変えた時のそれぞれの状態パターン($ξ^{new}$に相当)を示したものである。
(※なお、$ξ^{new}$の更新則 式(22)は1更新ステップで収束する)
4. 拡張その3:複数の状態パターンへの拡張→self-attentionになる
- 複数のパターンを一度に更新できるようにする
- associative spaceにパターンをマッピングする
- 結果を射影する
の3ステップで拡張をする。これを行うことで、Transformerに使われるself-attentionと同じものを得ることができる。
補足(トグル開く): ここが何を言っているかがわかりづらいので補足する。
今まではX自体を更新していたが、Xはあくまで生のパターンではなくて、生のパターンYに対して変換をして隠れ状態Xを得るというような方法を使う。
これはself-attentionの式と表記を合わせるためではないかと思われる。
式の上では $X^T = Y W_K$ という対応関係がある。つまり、$Y$を重み$W_K$で変換したものが$X^T$であるというような捉え方をする。
このことを、$Y$を「associative spaceにマッピングする」と呼んでいる。
また、最後に得られたパターンを$Y$と同じ次元に戻して出力を得る必要があるので、
出てきた結果を$W_V$という行列で変換してあげることになる。
後述の出力$Z$は、$Z = $(associative spaceの出力値)×$W_V$ という形をしている。
これで元のYの生のパターンの次元に戻せたことになる。
まずは、パターンを複数同時に更新できるようにする。
S個の状態パターン $ξ$ が並んだものを $\rm Ξ$ (※大文字のξ) として定義する。
式を順当に拡張すると下図のようになる。
(※補足:この拡張はTransformerに帰着させることを見据えてトークン列を一気に更新できるようにするためのものとなっている)
更新式(21)はこのように拡張される。
$$\mathrm{Ξ}^{new}=X \mathrm {softmax} (βX^T \mathrm Ξ) \tag{23}$$
やっていることは同じで、記憶させたパターンと状態パターンの内積を取って、その類似度に応じて$x$を重みづけた和を取ることで、想起したパターン $\rm Ξ^{new}$ を作り出している。
次に、$X$は記憶したい生のパターン$Y$を変換したもの、$\rm Ξ$は生の状態パターン$R$を変換したものだった、ということにする。
$$\begin{align}
\mathrm Ξ^T &= RW_Q (= Q) \tag{24} \\
X^T &= YW_K (= K) \tag{25}
\end{align}
$$
つまり、$X$や$\rm Ξ$は隠れ層の状態に該当するというようなことになる(現記事ではassociative spaceと呼んでいる)。
(※ここが分かりづらい場合は、上の補足のトグルが参考になる)
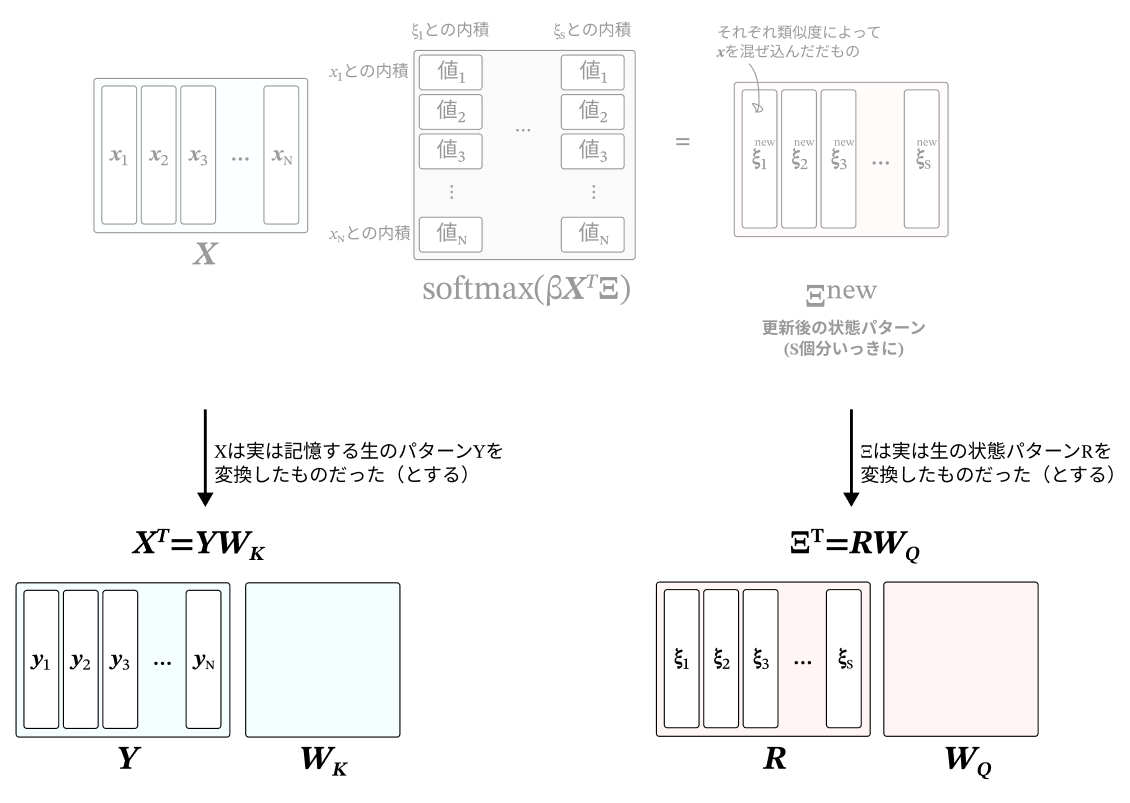
一度associative spaceの空間に射影してしまっているので、出てきた出力を再度入力と同じ空間に戻すために、
softmaxの値に対して行列 $K_V$ をかける。
ここまでを式変形の形で説明する。式(23)から出発して、
$$\mathrm{Ξ}^{new}=X \mathrm {softmax} (βX^T \mathrm Ξ) \tag{23}$$
これをRとYを使った式に変えて、
$$\mathrm{Ξ}^{new}=(YW_K)^T \mathrm {softmax} (β YW_K (RW_Q)^T) \tag{23'}$$
元の空間に戻すために$W_V$をかける。得られた出力を$Z$と呼んでおく。
$$Z^T=W_V^T (YW_K)^T \mathrm {softmax} (β YW_K (RW_Q)^T) \tag{23''}$$
(全体を転置すると原文の式(30)と一致する)
$$Z = \mathrm{softmax} (β \cdot R W_Q W_K^T Y^T)YW_KW_V \tag{30}$$
これで式自体としては完成している。
ここからは、この式がTransformerのself-attentionと対応しているということを示しに行く。
式(24)、式(25)に加えて、$β=\frac{1}{\sqrt{d_k}}$ の仮定を置く。
式(23')を置き換えると、
$$(Q^{new})^T=K^T softmax(\frac{1}{\sqrt{d_k}}KQ^T)$$
全体を転置して
$$Q^{new} = softmax(\frac{1}{\sqrt{d_k}}QK^T)K$$
$W_V$をかけて$Z$を得る。途中で$V=KW_V$と定義した$V$に置き換える。
$$ \begin{align}
Z &= Q^{new} W_V \\
&= \mathrm{softmax}(\frac{1}{\sqrt{d_k}}KQ^T)KW_V \\
&= \mathrm{softmax}(\frac{1}{\sqrt{d_k}}KQ^T)V
\end{align} \tag{29}$$
これでTransformerのself-attentionと完全に一致する。
記事内容への補足
- この記事のEnergyと $ξ$ の更新式については、Krotov et al. (2020) ではさらに2層のニューラルネットワークで表せることが示されている。
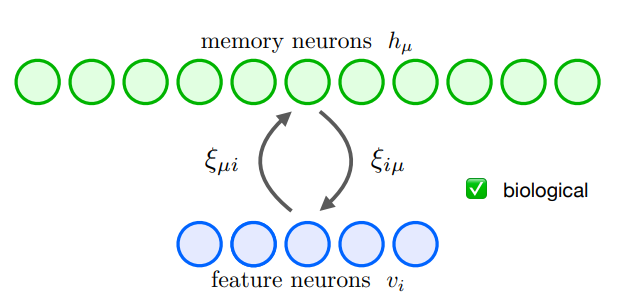
変数名がこの記事と異なるので、読み替え表を下に付す。
| 変数 | 本記事 | Krotov+ (2020) |
|---|---|---|
| 状態パターン | $ξ$ | $v_i$ |
| 記憶させるパターン列 | $X$ | $ξ_{iμ}$ |
-
Lu & Wu (2023)ではさらに時系列のシーケンスをパターンとして学習させられることが示されている。
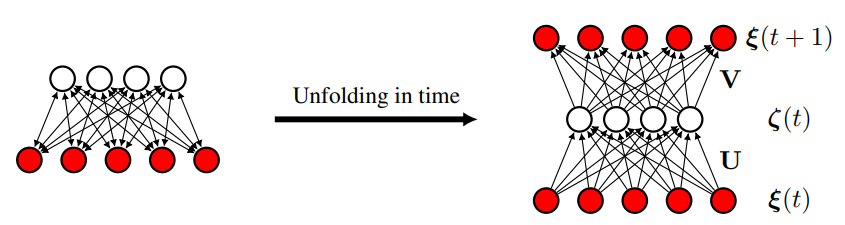

Krotov+ (2020) ではフィードフォワードとフィードバックワードが同じ行列(の転置)になっていたのに対して、シーケンス学習では、UとVの2つの行列を学習している。
今のパターンがUのどれと似ているかを計算したうえで、別の行列Vで展開することによって、1次の遷移が学習させられているということになる。 -
$ξ$とパターンそれぞれとの内積を取りsoftmaxで類似度にしたうえで、再度パターンで掛け算して予測を作るというのは、結構当たり前なことをしている。これだけでも2値の値なら連想記憶を作ることはできる。
Continuous Modern Hopfield Networkでは、$\frac{1}{2} ξ^T ξ$の項が入っていることで$ξ$が有限の範囲でパターンの検索ができるようになっている
($ξ$のノルムを大きくすることにペナルティが入っていると言える)。
本記事筆者の疑問点 (分かる方いらっしゃればコメント欄にください)
- パターン $X$ を丸覚えするのでなく、各パターン $x_i$ をオンライン学習的に提示しながら、$X$ (Krotov+(2020)でのシナプス重みξ) を学習させる方法はあるだろうか?
- 統計力学、変分ベイズの自由エネルギーとの関連について。
エネルギーの第1項は、$-lse(β,X^T ξ) = -\frac{1}{β} \log (\sum_l e^{β X^T ξ}_{[l成分]}) $
という形をしていて、
$\sum_l e^{β X^T ξ}_{[l]}$の部分は統計力学の分配関数(Z)と同じ形だ。
すなわち $-\log Z$ という形をしている。
変分ベイズ法では、$-\frac{1}{β} \log Z$ の部分が自由エネルギーの最小値(変分下界, ELBO)を与える。
($- \log p(o)$ ($o$: 観測) に当たる)
Modern Hopfield Networkにおいても、ここの値が最適化によってエネルギーを下げたときの下限になるのだろうか?
そうだとすると自由エネルギーとここでのエネルギーEはどのような関係になるのだろうか?
-
この元記事は、Ramsauer et al. (2021)が元となっている。 https://arxiv.org/abs/2008.02217 ↩