※この記事は書きかけです
初めに
粒子法というのは、天文学などで多く使われる数値計算手法の一つで、
世の中の運動量保存則などは全て粒子間相互作用にコンバートされる。
粒子法は、馬鹿正直に計算を行うと、自分の周りの粒子全てとの相互作用を計算することになるため、
粒子数を$N$とすると、$N^2$の計算コストがかかる事になる。
そこで、一般的にはTree法と呼ばれる手法(Barnes & Hut, 1986)と、並列計算(e.g., OpenMP, MPI)などを組み合わせて、高速な計算を行う。
とは行っても、並列Tree法で性能を出そうと思うと、結構難しいコーディングを強いられる事になる。
そこで、これを何とか解決するために開発されたソフトウェアが、以上の事を自動で行ってくれるソフトウェアFramework for Developing Particle Simulator、略してFDPSである( http://www.jmlab.jp/?p=503&lang=ja )。
というか僕も頑張って開発のお手伝いをしましたとも。
で、悲しいかなこれでど偉いコア数のCPU買ってくれば早くなるんでしょヒャッホイとは行かない。
というのも、
(1)Tree法は粒子数の少ないところでは普通に計算するより遅くなる。
(2)OpenMPはコア数をつぎ込んでも単純に早くなるとは限らない。
という事があるからである。
今回はそれを実際に見てみよう。
計算する方程式
今回はシンプルに重力を解くことにする。
即ち、
\frac{\mathrm{d}^2 \vec{r}_i}{\mathrm{d} t^2} = - \sum_j \frac{m_j}{|\vec{r}_{ij}|^2} \hat{{r}}_{ij}
である。
これは明らかに$N^2$の計算量が必要な計算である。
これを、Tree法を用いて$N \log_8(N)$の計算コストにしてくる。
計測
以下、FDPSの使い方は特に説明しない。
とにかく、$[0, 1]^3$の計算boxに、$N$個の粒子をランダムにばらまき、1回の相互作用計算にかかった計算時間を見る。
計測は$N$を$2$からスタートして、2倍ずつ上昇させていく。
また、同時に並列計算に用いたコア数も$1$から順番に2倍にしていく。
計測に用いたのはIntel(R) Xeon(R) CPU E5-2670 v3 @ 2.30GHzで、これは12コア24スレッドである。
時間の計測にはCの関数gettimeofdayを用いた。
また、ばらつきを抑えるために以上の測定を何回か行って13回ほど行った。
コード
省略…そのうちgithubとかにあげるかも
結果
まずは横軸を粒子数、縦軸を計算時間に取る。
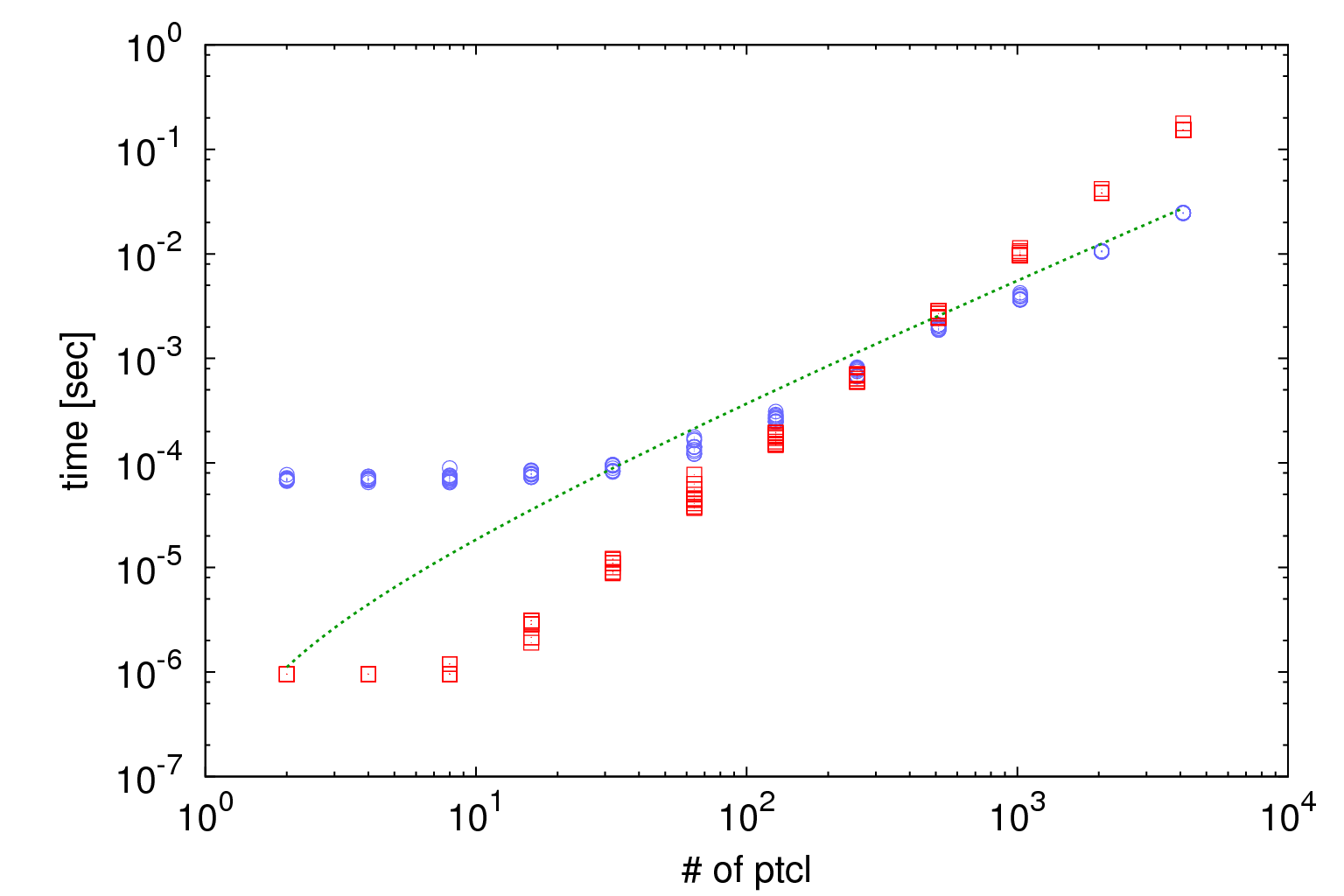
青の点がTree法を用いた際の計測点、赤が$N^2$計算の計測展で、緑のカーブが$N log_8(N)$である。
使用コア数は1コアのみとした。
これから見て分かる通り、粒子数が少ないところ($N < 2048$)では、ダイレクト計算の方が早い。
これは、そもそもTree構造の生成に時間がかかるからであり、粒子数が少ない部分ではTreeを作らず正直に$N^2$するほうが早いという事である。
次に、横軸をコア数、縦軸を計算時間に取った物を表示した。
粒子数は65536である。
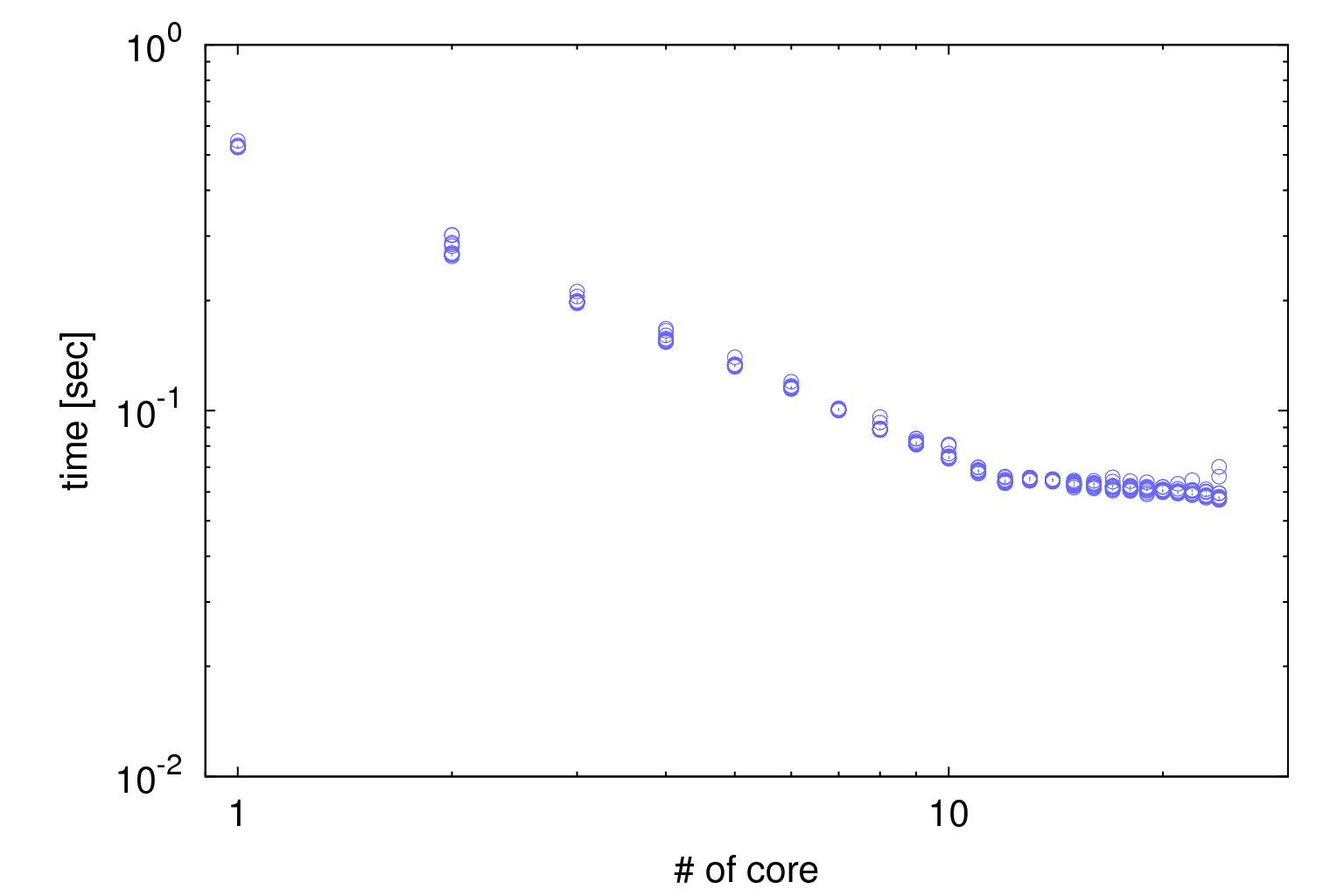
これから、12スレッドのところまでは順調に計算時間が落ちていくが、そこから先は少し落ち悩む。
(コレなんでなんだっけ?同期?キャッシュ?)
多分HTのせいで物理的な演算装置が増えてないので、ここで一旦折れ曲がる。
また、24スレッドフルに使うと、たまに計算時間が跳ね上がる点がある。
多分これはOS jitterか何かだと思われるため、安全をきすなら24スレッド全部使うのではなく、
23とか22とかあたりにしておくと防げる。
あるいは、12スレッドの計算を2本流すとか。
結論
というわけで、Tree vs. Directの計算時間比較をしてみたり、コア数依存性を見てみたり。
「早くなる」と伝え聞いたからそれを使う、のではなく、自分がやりたい計算にとって最も効率的なconfigurationを選んできましょう。