matplotlibで3DのScatter plotを使ってみようと思ったらサーバーに入ってるversionが古かった記事、はぁじまーるよー(ゆっくりボイス)
初めに
粒子的数値計算の可視化を3Dでかっこ良くやりたいなと思いまして、
具体的には
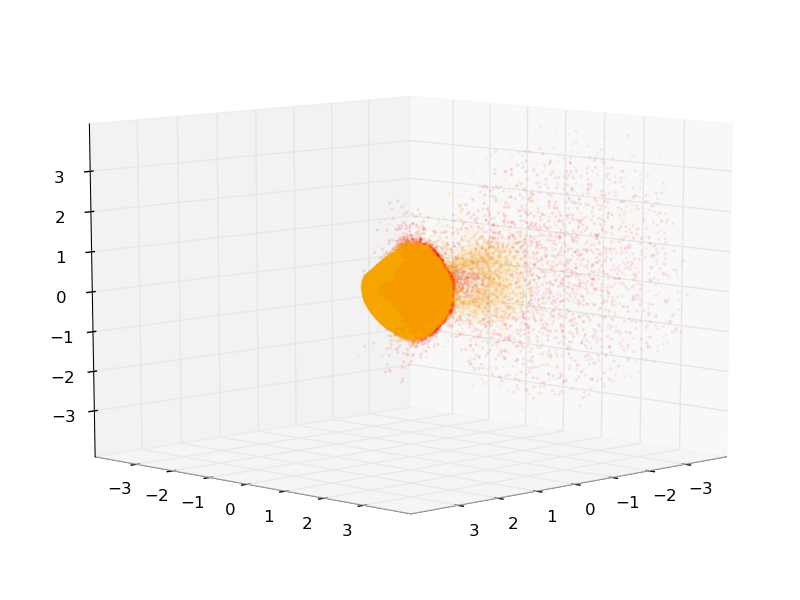
↑こういうのを作りたいなと思ったわけです。
一級gnuplot師のわたくしと致しましてもgnuplotでやりたいなぁと思ったわけですが、
一方でたまには違うplotter使いたいなぁと思ったので、頑張ってmatplotlibで作ってみました。
matplotlib
matplotlibはPythonで動く可視化ライブラリです。
scriptはこちら。
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
box_size = 4.0
R = 6400.0e+3
print mpl.__version__
fig = plt.figure()
# if version > 1.0.0
# ax = plt.add_subplot(111, projection='3d')
start = 0
stop = 1
step = 1
Nnode = 4
for step in range(start, stop, step):
print step
tag = []
x = []
y = []
z = []
for n in range(Nnode):
data = np.loadtxt("./result/%05d_%05d_%05d.dat" % (step, Nnode, n), skiprows=2, delimiter="\t");
tag.extend(data[:,1])
x.extend(data[:,3])
y.extend(data[:,4])
z.extend(data[:,5])
x_tag = [[], [], [], []]
y_tag = [[], [], [], []]
z_tag = [[], [], [], []]
size_tag = [[], [], [], []]
for i in range(len(x)):
x[i] = x[i]/R
y[i] = y[i]/R
z[i] = z[i]/R
x_tag[int(tag[i])].append(x[i])
y_tag[int(tag[i])].append(y[i])
z_tag[int(tag[i])].append(z[i])
size_tag[int(tag[i])].append(1.0)
clr = ["orange", "gray", "red", "black"]
ax = Axes3D(fig)
for tag in range(4):
ax.scatter(x_tag[tag], y_tag[tag], z_tag[tag], s=size_tag[tag], c=clr[tag], edgecolor=clr[tag], alpha=0.1)
ax.set_aspect('equal')
ax.set_xlim3d(-box_size, box_size)
ax.set_ylim3d(-box_size, box_size)
ax.set_zlim3d(-box_size, box_size)
ax.view_init(9.0, 45.0)
#plt.show()
plt.savefig("./img/%05d.png" % step)
解説
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
まずはimport。
box_size = 4.0
R = 6400.0e+3
定数の宣言。
print mpl.__version__
fig = plt.figure()
# if version > 1.0.0
# ax = plt.add_subplot(111, projection='3d')
matplotlibのversionを出力しときました。
matplotlibはversionによって3D plotのやり方が違うので…。
start = 0
stop = 1
step = 1
start から stop まで、stepずつインクリメントしながらグラフを作る。
tag = []
x = []
y = []
z = []
配列の初期化。
for n in range(Nnode):
data = np.loadtxt("./result/%05d_%05d_%05d.dat" % (step, Nnode, n), skiprows=2, delimiter="\t");
tag.extend(data[:,1])
x.extend(data[:,3])
y.extend(data[:,4])
z.extend(data[:,5])
計算結果がNnode個のファイルに分散しているので、一個ずつdataにloadtxtで読み込み、
先に定義しておいた配列にextendメソッドで突っ込んでいく。
今回の場合は1列目がtag, 3列目がx座標、4列目がy座標、5列目がz座標。
x_tag = [[], [], [], []]
y_tag = [[], [], [], []]
z_tag = [[], [], [], []]
size_tag = [[], [], [], []]
tag別に色を変えてplotするため、2次元配列を作る。
for i in range(len(x)):
x[i] = x[i]/R
y[i] = y[i]/R
z[i] = z[i]/R
x_tag[int(tag[i])].append(x[i])
y_tag[int(tag[i])].append(y[i])
z_tag[int(tag[i])].append(z[i])
size_tag[int(tag[i])].append(1.0)
clr = ["orange", "gray", "red", "black"]
規格化定数で座標を割った後、データを対応するtagの配列に突っ込んでいく。
それが終わったらtagに対応する色を定義する。
ax = Axes3D(fig)
for tag in range(4):
ax.scatter(x_tag[tag], y_tag[tag], z_tag[tag], s=size_tag[tag], c=clr[tag], edgecolor=clr[tag], alpha=0.1)
Axes3Dクラスを作り、scatterにデータを流し込む。
これはtag毎に行う必要がある。
今回size_tagは固定にしておく。
edgecolorはclr[tag]にしておく。
これによりフチのない粒子で描ける。
透過率alphaは一貫して0.1。
ax.set_aspect('equal')
ax.set_xlim3d(-box_size, box_size)
ax.set_ylim3d(-box_size, box_size)
ax.set_zlim3d(-box_size, box_size)
ax.view_init(9.0, 45.0)
今回はアスペクト比が全て等しくする。
また、各軸のrangeを設定する。
view_initで、カメラの角度を設定。
#plt.show()
plt.savefig("./img/%05d.png" % step)
出力する。普通にshow()してもいいんだけど今回はsavefigでpngにしてあとでアニメgifにする。
ね?簡単でしょう?