はじめに
我々の太陽には、活発な磁気活動があります。磁気活動が穏やかな時は太陽表面ものっぺりしており平和なのですが、磁気活動が活発になると黒点が多く出現しフレアと呼ばれる高エネルギー爆発現象が引き起こされたりします。太陽の磁気活動は周期性を持っていることが知られており、太陽内部のダイナモ機構によって周期的な磁場生成が維持されていると考えられています。
David Hathaway 氏のウェブサイト
NASA の Marshall Space Flight Center の David Hathway 博士のウェブサイトには、太陽の磁気活動や流れ場に関する様々な観測データが公開されています。
http://solarcyclescience.com/index.html
今回は、主にこれらの公開データをダウンロードして実際にプロットしながら遊んでみたいと思います。
太陽黒点面積データ
まずはじめに太陽黒点面積データをダウンロードしてきます。
wget http://solarcyclescience.com/AR_Database/sunspot_area.txt
テキストファイルで列データはそれぞれ(#1)年(#2)月(#3)黒点面積となっています。Python を使ってこのデータを読み込んで図示してみます。
import numpy as np
import matplotlib.pyplot as plt
#read data
data = np.loadtxt("sunspot_area.txt",skiprows=1)
year = data[:,0]
month = data[:,1]
ssa = data[:,2]
#time format
time = year+month/12.0
#total area of visible hemisphere
Rsun = 696 #[Mm]
Stot = 0.5*np.pi*(Rsun**2)
#--- figure ---#
fig = plt.figure(figsize=(10,3))
plt.rcParams["font.size"] = 12
ax = fig.add_subplot(111)
ax.plot(time,ssa/Stot*100,'-k',linewidth=0.5)
ax.set_xlabel('Year')
ax.set_ylabel('Sunspot area [%]')
ax.set_xlim(time[0],time[-1])
ax.set_ylim(0,0.6)
plt.subplots_adjust(top=0.9,bottom=0.2)
plt.show()
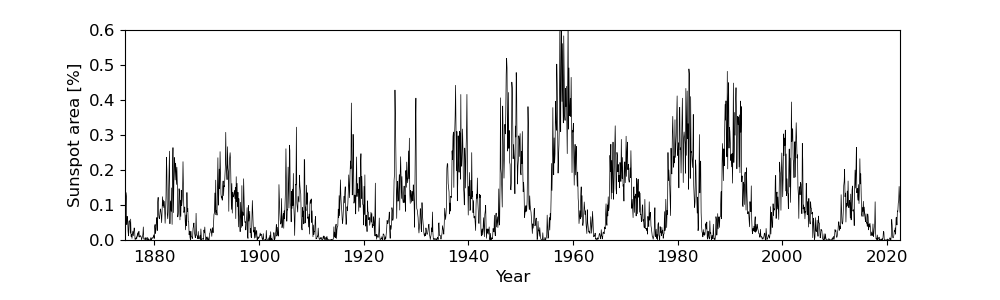
ここで、黒点面積は [Mm$^{2}$] として与えられているので、太陽半面(片方の半球)における全体の面積で割ったパーセント表示しています。
約 11 年周期で増減を繰り返していることがわかります。フーリエ変換してみたら面白そうです。
太陽黒点数データ
せっかくなので、ついでに太陽黒点数データとも比較してみましょう。これはベルギー王立天文台 SILSO が公開しているデータをとってきます。
wget https://www.sidc.be/silso/DATA/SN_m_tot_V2.0.txt
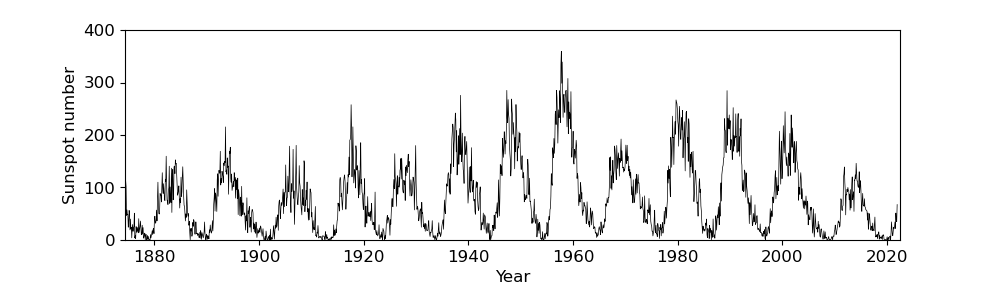
同様のプロットしてみたのが下図です。基本的に黒点面積データとほぼ同じ振る舞いをしていることがわかります。つまり個々の黒点の大きさは大体いつも決まっていて、単純に黒点数が多い時に黒点面積が増えるということを示しています。
太陽黒点面積の蝶形図(バタフライ・ダイアグラム)
続いて、緯度毎に経度平均した黒点面積データを見てみましょう。公開データを拾ってきて、
wget http://solarcyclescience.com/AR_Database/bflydata.txt
以下の Python スクリプトで読み込み・プロットを行います。
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
#read file
f = open('bflydata.txt')
data = f.readlines()
f.close()
#number of temporal points
Nt = round(len(data)/6)
yr_start = 1874.31935 #carrington rotation 275
yr_end = 2022.47773 #carrington rotation 2258+1
year = np.linspace(yr_start,yr_end,Nt)
#number of latitudinal points
Ntheta = 50
latsin = np.linspace(1,-1,Ntheta)
latdeg = np.arccos(latsin)*180/np.pi-90
#substitute corresponding data
Crot = np.zeros(Nt)
Bfly = np.zeros([Nt,Ntheta])
for i in range(Nt):
n = i*6
Crot[i] = float(data[n])
for j in range(n+1,n+6):
list = data[j].split(',')[0:10]
for k in range(10):
Bfly[i,k+10*(j-n-1)] = float(list[k])
#from sunspot area [Mm^2] to % per latitude
Rsun=696.0
for j in range(Ntheta):
Atot = (4.0/50)*np.cos(np.arcsin(abs(latsin[j])))
Bfly[:,j]=Bfly[:,j]/Atot/(Rsun**2)*100.0
Bfly_new = np.where(Bfly<1.0e-3,-1,Bfly)
#--- figure ---#
fig = plt.figure(figsize=(10,3))
plt.rcParams["font.size"] = 12
cmap = plt.cm.viridis
cmap.set_under('w')
ax = plt.subplot(111)
#plot data
im = ax.pcolormesh(year,latdeg,np.transpose(Bfly_new),cmap=cmap,vmin=0.0,vmax=0.6)
ax.set_xlabel('Time [yr]')
ax.set_ylabel('Latitude [deg]')
ax.set_xlim(year[0],year[-1])
ax.set_ylim(-60,60)
#set axis
ax.xaxis.set_minor_locator(mpl.ticker.MultipleLocator(10))
ax.yaxis.set_major_locator(mpl.ticker.MultipleLocator(30))
ax.grid(which='both',axis='both',alpha=0.5)
#add colorbar
cb=plt.colorbar(im,aspect=30,extend='both',shrink=0.9,pad=0.02,orientation='vertical',extendfrac=[0.05,0.05])
cb.set_label("Sunspot area [%]")
plt.subplots_adjust(top=0.9,bottom=0.2,left=0.1,right=0.99)
plt.show()
このデータでは、黒点面積は各太陽自転(キャリントン回転数)ごとに計算されているので、この表に従ってこれを年に変換しています。このデータファイルは David Hathaway氏によって随時更新されているので、適宜 year_end パラメータを最新のキャリントン回転数に対応させる必要があります。
また、経度平均した各緯度での黒点面積は [Mm$^{2}$]で与えられているので、これも各緯度におけるストライプの面積で割ったパーセントに変換しました。
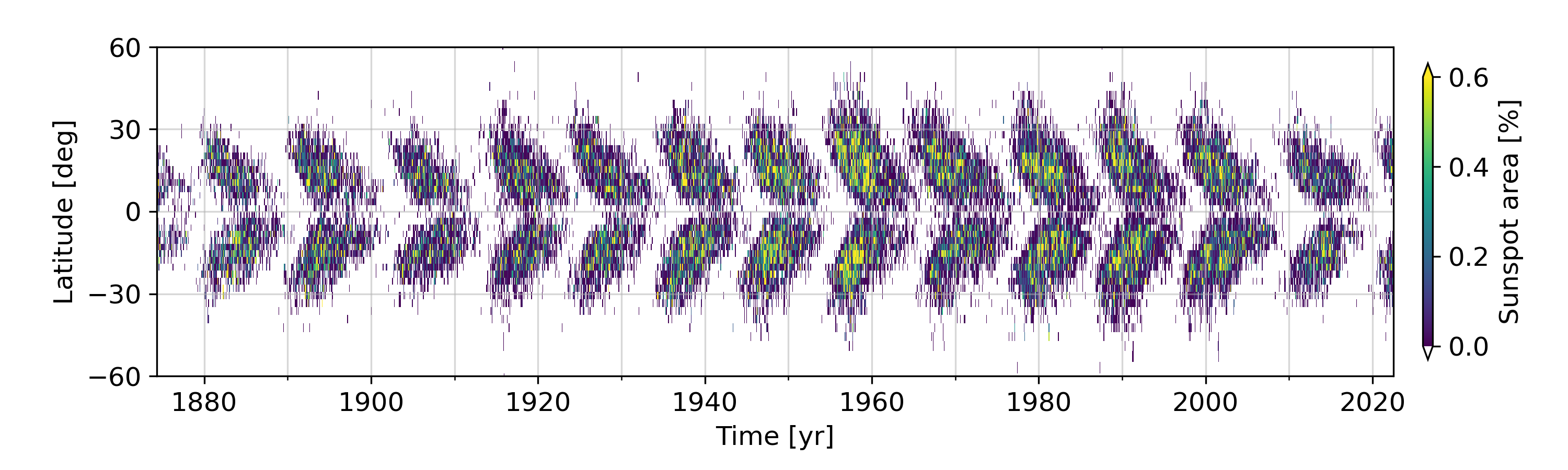
横軸を時間・縦軸を緯度として、黒点面積をプロットしたものが上図です。これは、まるで蝶々が羽を広げたような模様をしているので「蝶形図(バタフライ・ダイアグラム)」と呼ばれています。
約 11年周期で、黒点は最初中緯度(30度くらい)に出現し、その後時間の経過とともに出現緯度が赤道方向に移動していく様子が示されています。この観測事実は Spörer(シュペーラー)の法則として知られています。
太陽表面磁場の蝶形図(バタフライ・ダイアグラム)
せっかくなので、太陽表面磁場データでも同様の蝶形図を作成して、比較してみましょう。
ちなみに、実は太陽黒点観測に歴史は古く、1600年代初頭のガリレオ・ガリレイの黒点スケッチまで遡ります。しかしながら、「黒点は非常に強い磁場の断面である」ことが判明したのは、ゼーマン効果が発見された後 1900年代初頭でした。1950年代になると、現在でも使われている マグネトグラフと呼ばれる装置で精度良く太陽表面磁場の定常観測ができるようになりました。
今回使用する磁場データはアメリカ国立太陽天文台(NSO)のキット・ピーク真空望遠鏡(KPVT)データなのですが、1975年に観測が始まり現在までに約4太陽サイクル分をカバーしています。以下の python スクリプトを用います。
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
from matplotlib.colors import LinearSegmentedColormap
#read data
npz = np.load('bfly_mag.npz')
time = npz['arr_0']
sinlat = npz['arr_1']
data = npz['arr_2']
#use original colormap
vals = [0.0,0.15,0.4,0.48,0.5,0.52,0.6,0.85,1.0]
cols = ['darkblue','blue','cyan','white','lightgrey','white','yellow','red','darkred']
color_list=[]
for v,c in zip(vals,cols):
color_list.append((v,c))
my_cmap = LinearSegmentedColormap.from_list('my_cmap', color_list)
#--- figure ---#
fig = plt.figure(figsize=(13,3.6))
plt.rcParams["font.size"] = 13
ax = fig.add_subplot(111)
#plot data
im = ax.pcolormesh(time,sinlat,np.transpose(data),cmap=my_cmap,vmin=-8,vmax=8)
ax.set_xlim(time[0],time[-1])
ax.set_ylim(-1,1)
ax.set_xlabel('Time [yr]')
ax.set_ylabel('Latitude [deg]')
#grid axes
ax.xaxis.set_minor_locator(mpl.ticker.MultipleLocator(5))
ax.xaxis.set_major_locator(mpl.ticker.MultipleLocator(10))
ax.yaxis.set_major_locator(mpl.ticker.MultipleLocator(0.5))
ax.set_yticks(ticks=[-1,-0.5,0,0.5,1],labels=['-90','30','0','30','90'])
#add colorbar
cb = fig.colorbar(im,ax=ax,aspect=25,pad=0.015,shrink=1,orientation='vertical'
,ticks=[-8,-4,0,4,8],extendrect='True',extendfrac=0)
cb.set_label(r"Radial field $B_{r}$ [G]")
plt.subplots_adjust(top=0.92,bottom=0.18,left=0.15,right=1)
plt.show()
LinearSegmentedColormap 機能を使って独自のカラーマップ(基本的には [青/白/赤]だが 値が0の時だけグレー)を作成しプロットに使用しています。また、縦軸は緯度のサインで与えています。
プロットした結果が下図になります。ここから色々な面白いことが分かります。
まず、はっきりとした南北反対称性が挙げられます。特に、太陽活動が穏やかな期間は磁場は極域に局在化しており双極型の磁場形状であることが分かります。そして、そのような双極磁場は約 22 年の周期で反転を繰り返していることも確かめられます。つまり、黒点数の 11年周期は本来の磁場周期の半分だったんですね。
一方、低緯度帯に注目すると、黒点出現緯度に対応した蝶々模様が確認できます。極域磁場の極性反転現象は、この低緯度帯における黒点出現が関係しているのではないかということも予想されます。
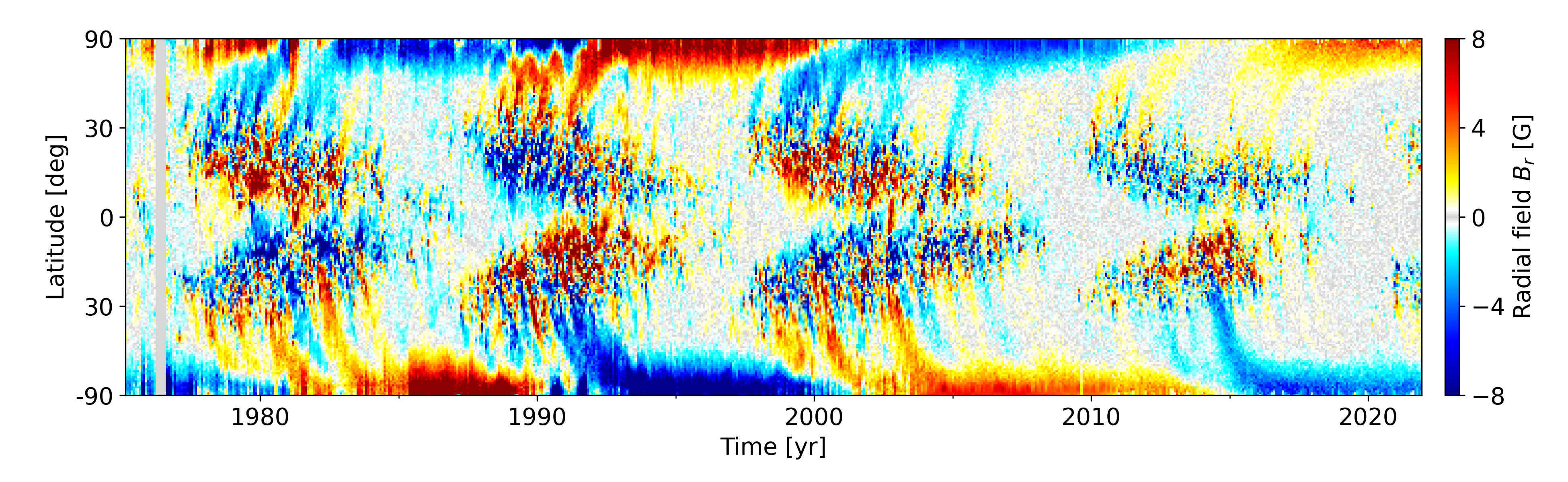
あと気になるのは、近年は太陽の磁気活動が 20年前と比較して俄然弱くなっていることです。このまま行くと数十年後には太陽の磁気活動がストップしてしまいそうな勢いですが、大丈夫でしょうか。何はともあれ、2020年からまた新たな太陽サイクルが始まったので、今後の磁気活動がどうなるのか是非とも注目していきましょう。
まとめ
このように、様々な面白いことが観測データから読み取れるのですが、実は理論的にはまだまだ分かっていないことが多いようです。特に、太陽黒点の起源・11年周期の謎に関しては現在も決着がついておらず、盛んに研究が進められているようです。一説によれば、もしこの太陽磁場の謎が解明されればノーベル賞級だとか。