はじめに
動的計画法について学んだことを初心者視点でなるべく簡潔にまとめる
”Educational DP contest/DPまとめコンテスト(EDPC)”の問題を解くことを目標に進めていく
今回は簡単な問題を解きながら動的計画法の基礎を学ぶ
※※※ 参考にさせていただいた記事
動的計画法超入門! Educational DP Contest の A ~ E 問題の解説と類題集
典型的な DP (動的計画法) のパターンを整理 Part 1 ~ ナップサック DP 編 ~
具体的に学ぶ
問題
n個の整数 a[0],a[1],…,a[n−1]が与えられる。これらの整数から何個かの整数を選んで総和をとったときの、総和の最大値を求めよ。また、何も選ばない場合の総和は 0 であるものとする。
仮に3個の整数 1,-2,3が与えられたとする
n = 3
a[0] = 1
a[1] = -2
a[2] = 3
(a = [1 -2 3])
まず、全探索で考える
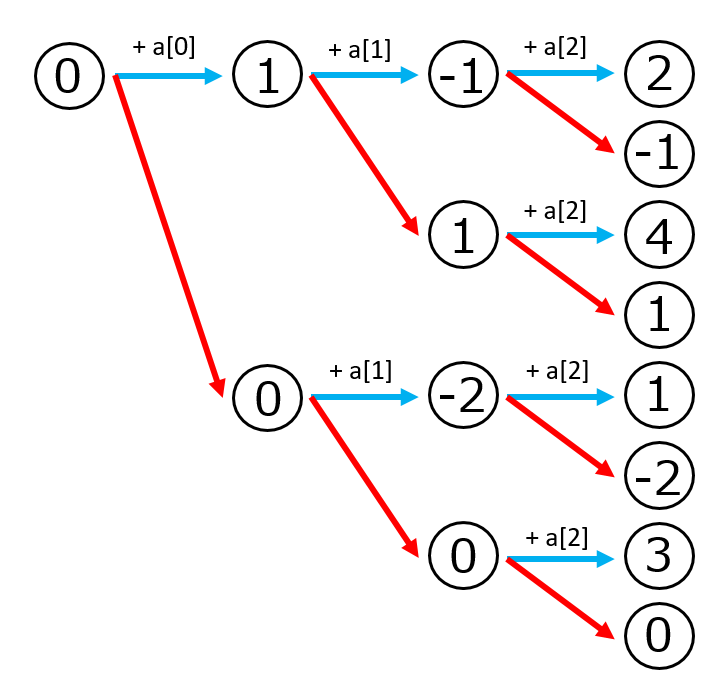
(青線はa[0~3]を足す操作、赤線は足さない操作)
右端の列の8個の数字が得られる
つまり、最大の値は4
このとき計算量はO(2^n)となり、nが大きくなると計算に時間がかかる
そこで、不必要な計算を除いていく
矢印を一つ進めるごとに出現する2つの数字を比較し、大きい方の数字だけ生かしていけばよい
小さい方の数字以降の計算は除外するように考える
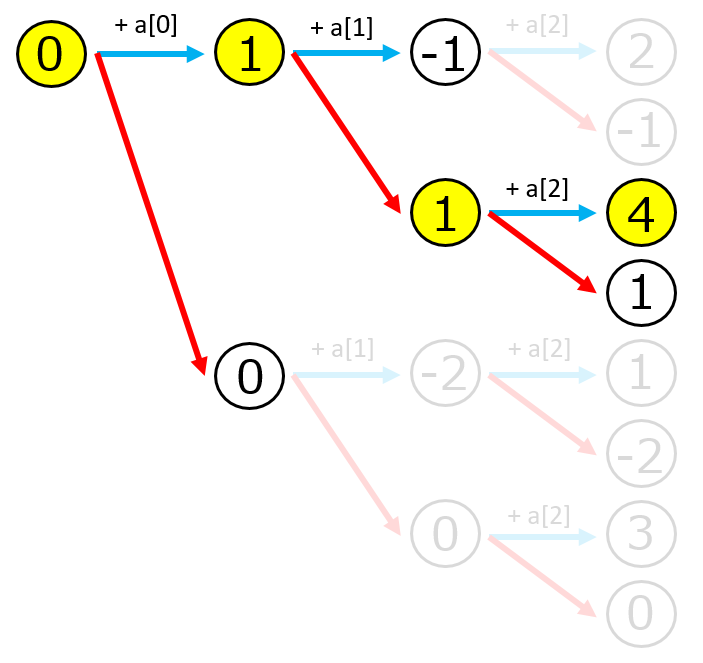
このとき、上図の黄色のマスを辿っていくことで最終的に最大値を得られることが分かる
この黄色マスのリスト(名前をdpとする)を作成することを目標とする
以下、実装手順
①黄色マスの数字を順番に保存するリスト(長さは4(=n+1)となる)を作成する
(※初期状態(dp[0]のこと)を0とする)
dp = [0]*4
②黄色マス2マス目 (dp[1]) への移動において、最大値をとるためには初期状態 (dp[0]) に a[0] を足した方が良いのかを判定する
dp[1] = max(dp[0],dp[0]+a[0])
③黄色マス3マス目 (dp[2]) への移動において、最大値をとるためには2マス目 (dp[1]) に a[1] を足した方が良いのかを判定する
dp[2] = max(dp[1],dp[1]+a[1])
④黄色マス4マス目 (dp[3]) への移動において、最大値をとるためには3マス目 (dp[2]) に a[2] を足した方が良いのかを判定する
dp[3] = max(dp[2],dp[2]+a[2])
⑤完成した黄色マスの数字リストから答えを出力する
(今回はリストの一番最後の数字のため dp[-1])
print(dp[-1])
まとめると
dp = [0]*4
dp[1] = max(dp[0],dp[0]+a[0])
dp[2] = max(dp[1],dp[1]+a[1])
dp[3] = max(dp[2],dp[2]+a[2])
print(dp[-1])
となる
これを拡張して、nがどんな値をとっても対応できるようにする
dp = [0]*(n+1)
dp[1] = max(dp[0],dp[0]+a[0])
dp[2] = max(dp[1],dp[1]+a[1])
dp[3] = max(dp[2],dp[2]+a[2])
...
...
...
dp[n-1] = max(dp[n-2],dp[n-2]+a[n-2])
dp[n] = max(dp[n-1],dp[n-1]+a[n-1])
print(dp[-1])
これをfor文を用いて表現する
dp = [0]*(n+1)
for i in range(n):
dp[i+1] = max(dp[i],dp[i]+a[i])
print(dp[-1])
これで完成
おわりに
動的計画法を簡単な具体例を用いて考えた
今後は実際の問題に対して応用していくことを考える
次回、EDPC_A,Bを解く