LoginSignup
29
22

More than 5 years have passed since last update.

@NariseT(T Narise)

遺伝子発現データを使用した機械学習

Last updated at Posted at 2017-02-02

遺伝子発現データを使用した機械学習

(2017.02.02 OSX El Capitan)

様々なヒト組織から取られた遺伝子発現データを使用して、遺伝子発現プロファイルから、
各々のサンプルが、どのヒト組織由来であるかを学習＆推論してみます。
Python 機械学習プログラミング を参考に実行してみました。

機械学習用遺伝子発現データの準備

GTEx Portal からデータを取得

GTEx Portal では、ヒトの様々な組織由来の遺伝子発現データが公開されています。
最新の GTEx Analysis V6p Release では、53 のヒト組織、544 のドナーから、
合計 8555 サンプルの遺伝子発現データが取得できます。

サイトにアカウント登録をすることで、遺伝子発現データをダウンロードできるようになります。
サイトのナビゲーションバーの Datasets -> Download から行けるページにダウンロードリンクがあります。

RPKM (Reads Per Kilobase of transcript per Million mapped reads) 補正された
遺伝子発現データのファイルには、以下のファイル名が付けられています。

  • GTEx_Analysis_v6p_RNA-seq_RNA-SeQCv1.1.8_gene_rpkm.gct.gz

GCT (Gene Cluster Text file format) フォーマットで提供されており、
列がサンプル（列名がサンプル名）、行が特徴量（行名が遺伝子名）となっています。

各サンプルのアノテーション（ラベル情報）は、
GTEx Analysis V6 Release で提供されており、以下のファイル名が付けられています。

  • GTEx_Data_V6_Annotations_SampleAttributesDS.txt

1列目にサンプルIDがあり、6列目と 7列目にどの組織由来かが記述されています。

GTEx_Analysis_v6p_RNA-seq_RNA-SeQCv1.1.8_gene_rpkm.gct.gz と GTEx_Data_V6_Annotations_SampleAttributesDS.txt
各ファイルのダウンロードリンクをクリックしてダウンロードをします。
続いて、.gz ファイルをダブルクリックして解凍します。

Unix / Linux コマンドでチェック

Linux コマンドを使用して、遺伝子発現データファイルの最初の 10行、3列を見てみます。
先頭 2行より、56238 遺伝子の発現量（特徴量）、8555 サンプルであることがわかります。
また、１列目の遺伝子名から Ensembl Gene ID が使用されていることがわかります。
発現量のデータ自体は、4行目の3列目からスタートしています。

cut -f1,2,3 GTEx_Analysis_v6p_RNA-seq_RNA-SeQCv1.1.8_gene_rpkm.gct | head
#1.2
56238   8555
Name    Description GTEX-111CU-1826-SM-5GZYN
ENSG00000223972.4   DDX11L1 0
ENSG00000227232.4   WASH7P  6.50895977020264
ENSG00000243485.2   MIR1302-11  0
ENSG00000237613.2   FAM138A 0
ENSG00000268020.2   OR4G4P  0
ENSG00000240361.1   OR4G11P 0
ENSG00000186092.4   OR4F5   0

遺伝子発現データの読み込み

python の pandas パッケージ read_csv を使用してデータを読み込みます。

タブ区切りなので、sep='\t'、最初の2行を skip したいため skiprows=2 としています。
最初に読み込まれる1行目がヘッダー（列名）となります。

2列目の Description を除いて、8555 サンプルのデータ（8557列目まで）を読み込みたいため、
usecols = [0] + list(range(2,8557)) としています。
そして、index_clo=0 として、1列目を行名に指定しています。

import pandas as pd

usecols = [0] + list(range(2,8557))
df1 = pd.read_csv('GTEx_Analysis_v6p_RNA-seq_RNA-SeQCv1.1.8_gene_rpkm.gct', sep='\t', skiprows=2, usecols=usecols, index_col=0)

>>> df1.index
Index(['ENSG00000223972.4', 'ENSG00000227232.4', 'ENSG00000243485.2',
       'ENSG00000237613.2', 'ENSG00000268020.2', 'ENSG00000240361.1',
       'ENSG00000186092.4', 'ENSG00000238009.2', 'ENSG00000233750.3',
       'ENSG00000237683.5',
       ...
       'ENSG00000198886.2', 'ENSG00000210176.1', 'ENSG00000210184.1',
       'ENSG00000210191.1', 'ENSG00000198786.2', 'ENSG00000198695.2',
       'ENSG00000210194.1', 'ENSG00000198727.2', 'ENSG00000210195.2',
       'ENSG00000210196.2'],
      dtype='object', name='Name', length=56238)
>>> df1.columns
Index(['GTEX-111CU-1826-SM-5GZYN', 'GTEX-111FC-0226-SM-5N9B8',
       'GTEX-111VG-2326-SM-5N9BK', 'GTEX-111YS-2426-SM-5GZZQ',
       'GTEX-1122O-2026-SM-5NQ91', 'GTEX-1128S-2126-SM-5H12U',
       'GTEX-113IC-0226-SM-5HL5C', 'GTEX-117YX-2226-SM-5EGJJ',
       'GTEX-11DXW-0326-SM-5H11W', 'GTEX-11DXX-2326-SM-5Q5A2',
       ...
       'GTEX-ZVE2-0006-SM-51MRW', 'GTEX-ZVP2-0005-SM-51MRK',
       'GTEX-ZVT2-0005-SM-57WBW', 'GTEX-ZVT3-0006-SM-51MT9',
       'GTEX-ZVT4-0006-SM-57WB8', 'GTEX-ZVTK-0006-SM-57WBK',
       'GTEX-ZVZP-0006-SM-51MSW', 'GTEX-ZVZQ-0006-SM-51MR8',
       'GTEX-ZXES-0005-SM-57WCB', 'GTEX-ZXG5-0005-SM-57WCN'],
      dtype='object', length=8555)

log変換、密度分布のプロット

読み込んだ 遺伝子発現量(RPKM) に pseudo count 1 を加えて log2 変換します。

import numpy as np

df1pc = df1 + 1
df1log = np.log2(df1pc)

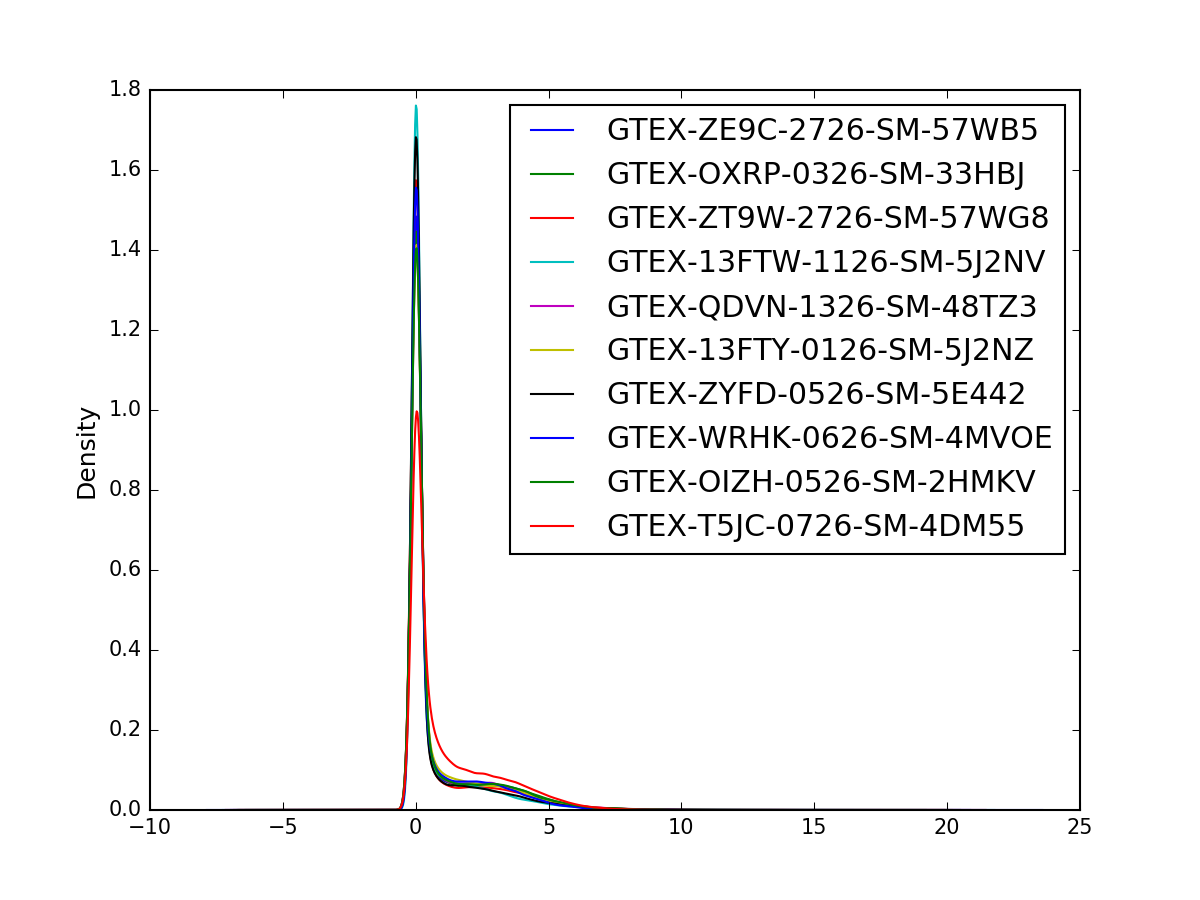
ランダムに 10 サンプルを選んで、遺伝子発現量の密度分布をプロットしてみます。
プロットには、pandas の DataFrame.plot.density を使用します。

import matplotlib.pyplot as plt

random_cols = np.random.choice(8555, 10)
df1log.iloc[:, random_cols].plot.density(fontsize=10)
plt.savefig('gtex_log_rpkm_density_random10sample.png', dpi=150)
plt.show()

gtex_log_rpkm_density_random10sample.png

サンプルごとに分布にかなり違いがあるため、トレーニングデータセットからリファレンスとなる分布を求めて
quantile 補正などを行った方が良いかもしれません。

サンプルの組織情報（クラスラベル）の読み込み

サンプルの組織情報が記載された GTEx_Data_V6_Annotations_SampleAttributesDS.txt から、
1列目のサンプルID、7列目の組織情報を読み込みます。

usecols = [0, 6]
df2 = pd.read_csv('GTEx_Data_V6_Annotations_SampleAttributesDS.txt', sep='\t', usecols=usecols, index_col=0)

遺伝子発現データの行と列を転置して、サンプルの組織情報のデータフレームと結合することで、
組織情報を付与します。pandas の concat を使用します。

df = pd.concat([df1log.T, df2], axis=1, join_axes=[df1log.T.index])

Python 機械学習プログラミング 4.2.2 (P99) より、
組織情報が文字列のままだと扱いづらいため、文字列を整数に変換して置き換えます。
遺伝子発現データを転置して結合したため、行がサンプル、列が特徴量と組織情報となります。

from sklearn.preprocessing import LabelEncoder

class_le = LabelEncoder()
label = class_le.fit_transform(df['SMTSD'].values)
label_r = class_le.inverse_transform(label)
df['SMTSD'] = label

トレーニングデータとテストデータに分割

Python 機械学習プログラミング 4.3 (P102) より、
ラベルを付けした遺伝子発現データを特徴量（X）とクラスラベル（y）に分割します。

smtsd_index = len(df.columns) - 1
X, y = df.iloc[:, :smtsd_index].values, df.iloc[:, smtsd_index].values

続いて、トレーニングデータとテストデータに分割します。

from sklearn.cross_validation import train_test_split

X_train, X_test, y_train, y_test = \
   train_test_split(X, y, test_size=0.3, random_state=0)

学習と推論

k近傍法 による学習と推論を行ってみます。
sklearn.neighbors.KNeighborsClassifier を使用します。

そろそろ不要な変数を削除して、メモリに余裕を持たせます。

del df
del df1
del df1pc
del df1log
del df2

k = 3、4並列で実行します。4GHz Intel Core i7 で 10分ほど計算時間がかかりました。

from sklearn.neighbors import KNeighborsClassifier

knn = KNeighborsClassifier(n_neighbors=3, n_jobs=4)
knn.fit(X_train, y_train)
print('Training accuracy: ', knn.score(X_train, y_train))
print('Test accuracy: ', knn.score(X_test, y_test))

以下のように、テストデータでの正解率は、約91% となりました。

>>> print('Training accuracy: ', knn.score(X_train, y_train))
Training accuracy: 0.95641282565130259
>>> print('Test accuracy: ', knn.score(X_test, y_test))
Test accuracy: 0.90962212699649392

遺伝子発現量による特徴量の選択

特徴量の選択を行います。遺伝子発現量の合計が 500 を超えない遺伝子は取り除いてしまいます。
Python 機械学習プログラミング 4.5.2 (P113) の逐次（ちくじ）特徴選択や
scikit-learn のソースコード を参考に、特徴選択するクラスを作成します。

from sklearn.base import TransformerMixin
import numpy as np

class GexSumFS(TransformerMixin):
    """
    Feature selection based on the sum of gene expression values
    """

    def __init__(self, sum):
        self.sum = sum

    def fit(self, X, y=None):
        self.indices_ = np.where(np.sum(X, axis=0) > self.sum)[0]
        return self

    def transform(self, X, y=None):
        return X[:, self.indices_]

上記のクラスを利用して、発現量の合計でフィルタリングをします。

sumfs = GexSumFS(sum = 500)
X_train_sumfs = sumfs.fit_transform(X_train)
X_test_sumfs = sumfs.transform(X_test)

遺伝子数（特徴量数）が 27754 まで減少しました.

>>> X_train_sumfs.shape[1]
27754

特徴選択したデータで学習＆推論してみます。

knn.fit(X_train_sumfs, y_train)
print('Training accuracy: ', knn.score(X_train_sumfs, y_train))
print('Test accuracy: ', knn.score(X_test_sumfs, y_test))

特徴選択前とほぼ同様、約91% の正解率となりました。
わずかに正解率が減少してしまいましたが、
特徴選択により、計算時間が少し減少するというメリットがありました。

>>> print('Training accuracy: ', knn.score(X_train_sumfs, y_train))
Training accuracy:  0.955577822311
>>> print('Test accuracy: ', knn.score(X_test_sumfs, y_test))
Test accuracy:  0.908843007402

遺伝子発現量を標準化（平均0、分散1）した場合だと、発現量の低い遺伝子はノイズとなりやすいため、
発現量による特徴選択がより効果的になるはずです。

Quantile normalization

密度分布のプロットから、サンプルごとに発現量の分布がかなり異なっていたため、
quantile 補正 を行ってから学習&推論をしてみます。
以下のように quantile 補正を行うクラスを作成します。

class QuantileNormalization(TransformerMixin):
    """
    Quantile normalization
    """

    def __init__(self):
        pass

    def fit(self, X, y=None):
        self.ref_dist_ = np.zeros(X.shape[1])
        X_rank = pd.DataFrame(X).rank(axis=1, method='min').astype(int)
        for i in range(X.shape[1]):
            indices = np.where(X_rank == i+1)
            if len(indices[0]) > 0:
                self.ref_dist_[i] = np.mean(X[indices])
            else:
                self.ref_dist_[i] = self.ref_dist_[i-1]
        return self

    def transform(self, X, y=None):
        X_norm = pd.DataFrame(X).rank(axis=1, method='min').values
        for i in range(X.shape[1]):
            X_norm[X_norm == i+1] = self.ref_dist_[i]
        return X_norm

上記のクラスを使用して quantile 補正を行います。
実装方法が悪かったためか、計算に丸一日かかりました。

q_norm = QuantileNormalization()
X_train_sumfs_qnorm = q_norm.fit_transform(X_train_sumfs)
X_test_sumfs_qnorm = q_norm.transform(X_test_sumfs)

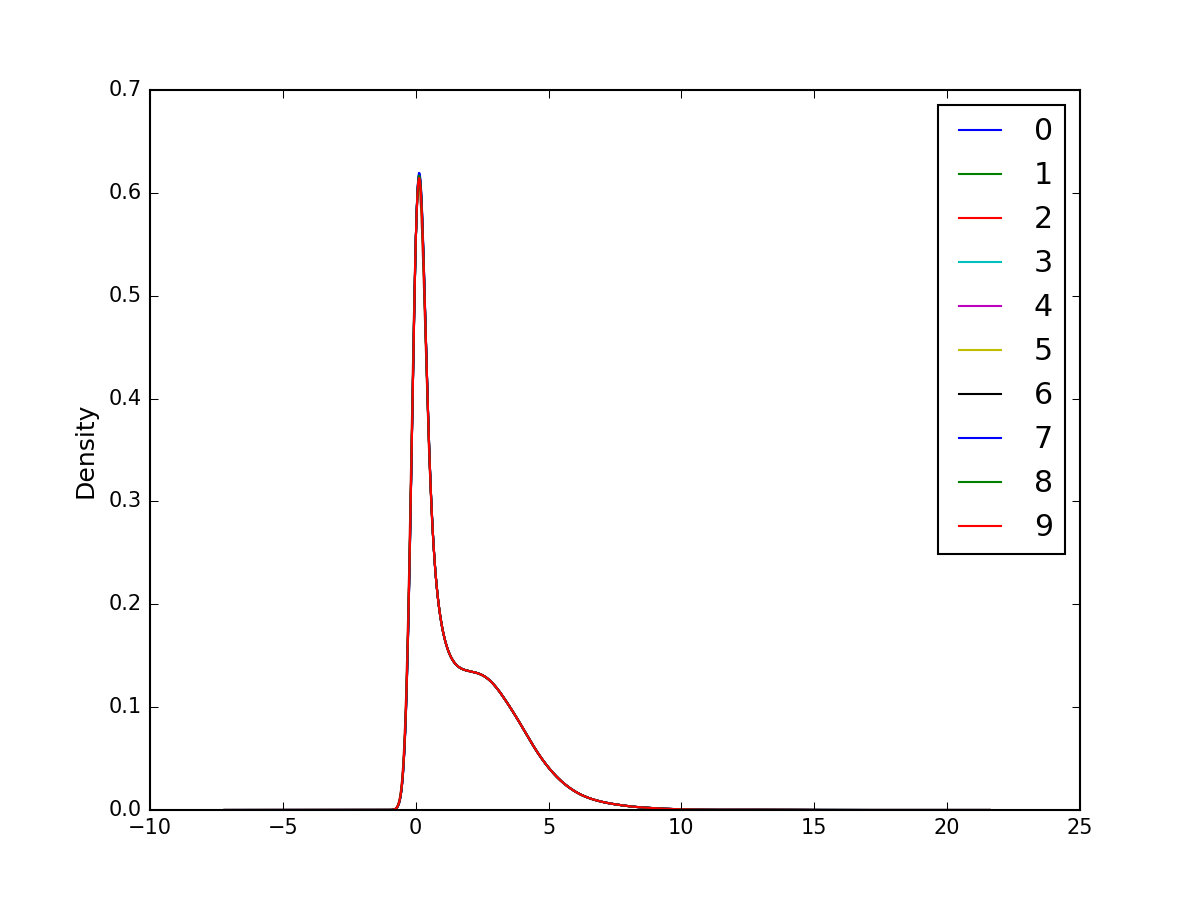
補正後の遺伝子発現プロファイルの密度分布を見て、密度分布が揃っていることを確認します。

random_rows = np.random.choice(range(X_train_sumfs_qnorm.shape[0]), 10)
pd.DataFrame(X_train_sumfs_qnorm[random_rows, :]).T.plot.density(fontsize=10)
plt.savefig('gtex_qnorm_density_random10sample.png', dpi=150)
plt.show()

gtex_qnorm_density_random10sample.png

quantile 補正をしたデータで学習＆推論してみます。

knn.fit(X_train_sumfs_qnorm, y_train)
print('Training accuracy: ', knn.score(X_train_sumfs_qnorm, y_train))
print('Test accuracy: ', knn.score(X_test_sumfs_qnorm, y_test))

推論の正解率が、0.6% ほど上昇しました。

>>> print('Training accuracy: ', knn.score(X_train_sumfs_qnorm, y_train))
Training accuracy:  0.956078824315
>>> print('Test accuracy: ', knn.score(X_test_sumfs_qnorm, y_test))
Test accuracy:  0.915855083755

標準化

Quantile 補正により分布を揃えたデータの標準化を行ってから学習＆推論を行ってみます。
Python 機械学習プログラミング 4.4 特徴量の尺度を揃える (P106) を参考にします。

from sklearn.preprocessing import StandardScaler

stdsc = StandardScaler()
X_train_sumfs_qnorm_std = stdsc.fit_transform(X_train_sumfs_qnorm)
X_test_sumfs_qnorm_std = stdsc.transform(X_test_sumfs_qnorm)

knn.fit(X_train_sumfs_qnorm_std, y_train)
print('Training accuracy: ', knn.score(X_train_sumfs_qnorm_std, y_train))
print('Test accuracy: ', knn.score(X_test_sumfs_qnorm_std, y_test))

>>> print('Training accuracy: ', knn.score(X_train_sumfs_qnorm_std, y_train))
Training accuracy:  0.951736806947
>>> print('Test accuracy: ', knn.score(X_test_sumfs_qnorm_std, y_test))
Test accuracy:  0.906505648617

今回の場合、標準化は、正解率を下げてしまうようでした。
非常に小さい分散を持つ遺伝子を標準化をすると、大きな値となってしまうことがあります。
正解率の低下は、このためかもしれません。

正規化

標準化ではなく、正規化（0〜1 にスケーリング）を行ってから学習＆推論を行ってみます。
Python 機械学習プログラミング 4.4 特徴量の尺度を揃える (P105) を参考にします。

from sklearn.preprocessing import MinMaxScaler

mms = MinMaxScaler()
X_train_sumfs_qnorm_norm = mms.fit_transform(X_train_sumfs_qnorm)
X_test_sumfs_qnorm_norm = mms.transform(X_test_sumfs_qnorm)

knn.fit(X_train_sumfs_qnorm_norm, y_train)
print('Training accuracy: ', knn.score(X_train_sumfs_qnorm_norm, y_train))
print('Test accuracy: ', knn.score(X_test_sumfs_qnorm_norm, y_test))

>>> print('Training accuracy: ', knn.score(X_train_sumfs_qnorm_norm, y_train))
Training accuracy:  0.952571810287
>>> print('Test accuracy: ', knn.score(X_test_sumfs_qnorm_norm, y_test))
Test accuracy:  0.910011686794

今回の場合、正規化も正解率を下げてしまうようでした。
正規化により、変動の少ない遺伝子の影響が大きくなってしまうためかもしれません。

分散の大きさによる特徴選択

分散の少ない遺伝子を事前に取り除くことで、標準化が効果的になるかもしれません。
以下のように分散の小さい特徴量を乗り除くクラスを作成します。

from sklearn.base import TransformerMixin
import numpy as np

class GexVarFS(TransformerMixin):
    """
    Feature selection based on the variance of gene expression values
    """

    def __init__(self, var):
        self.var = var

    def fit(self, X, y=None):
        self.indices_ = np.where(np.var(X, axis=0) > self.var)[0]
        return self

    def transform(self, X, y=None):
        return X[:, self.indices_]

上記のクラスを使用して、特徴選択（分散1 以下は削除）をした後に学習＆推論してみます。

varfs = GexVarFS(var = 1)
X_train_sumfs_qnorm_varfs = varfs.fit_transform(X_train_sumfs_qnorm)
X_test_sumfs_qnorm_varfs = varfs.transform(X_test_sumfs_qnorm)

knn.fit(X_train_sumfs_qnorm_varfs, y_train)
print('Training accuracy: ', knn.score(X_train_sumfs_qnorm_varfs, y_train))
print('Test accuracy: ', knn.score(X_test_sumfs_qnorm_varfs, y_test))

遺伝子数が減り、計算時間は大きく減少しましたが、
以下のように特徴選択により少しだけ正解率が低下してしまいました。

>>> print('Training accuracy: ', knn.score(X_train_sumfs_qnorm_varfs, y_train))
Training accuracy:  0.957915831663
>>> print('Test accuracy: ', knn.score(X_test_sumfs_qnorm_varfs, y_test))
Test accuracy:  0.913128165173

続いて、分散の大きさで特徴選択したデータの標準化を行い、学習＆推論します。

X_train_sumfs_qnorm_varfs_std = stdsc.fit_transform(X_train_sumfs_qnorm_varfs)
X_test_sumfs_qnorm_varfs_std = stdsc.transform(X_test_sumfs_qnorm_varfs)

knn.fit(X_train_sumfs_qnorm_varfs_std, y_train)
print('Training accuracy: ', knn.score(X_train_sumfs_qnorm_varfs_std, y_train))
print('Test accuracy: ', knn.score(X_test_sumfs_qnorm_varfs_std, y_test))

今回の場合は、標準化により、正解率が上昇しました。
また、特徴選択前と比べても、特徴選択＆標準化によって、若干正解率が上昇しました。

>>> print('Training accuracy: ', knn.score(X_train_sumfs_qnorm_varfs_std, y_train))
Training accuracy:  0.958750835003
>>> print('Test accuracy: ', knn.score(X_test_sumfs_qnorm_varfs_std, y_test))
Test accuracy:  0.918971562135

まとめ

最終的に推論の正解率は 約92% となり、log変換した RPKM値をそのまま使用した場合に比べて
1% ほど改善されました。主成分分析による次元削減や、
機械学習の手法を SVM などに変更することで、より良い結果が得られるかもしれません。

最後に組織ごとの正解率を調べてみます。

y_pred = knn.predict(X_test_sumfs_qnorm_varfs_std)
inv_dict = dict(zip(y, class_le.inverse_transform(y)))
for i in np.unique(label):
    accuracy_score = np.sum((y_pred[y_test == i] == i).astype(int)) / len(y_pred[y_test == i])
    print(inv_dict[i] + ': ' + str(accuracy_score))

Adipose - Subcutaneous: 1.0
Adipose - Visceral (Omentum): 0.984126984127
Adrenal Gland: 1.0
Artery - Aorta: 0.985294117647
Artery - Coronary: 0.911764705882
Artery - Tibial: 0.988636363636
Bladder: 1.0
Brain - Amygdala: 0.95
Brain - Anterior cingulate cortex (BA24): 0.76
Brain - Caudate (basal ganglia): 0.709677419355
Brain - Cerebellar Hemisphere: 0.838709677419
Brain - Cerebellum: 0.883720930233
Brain - Cortex: 0.864864864865
Brain - Frontal Cortex (BA9): 0.53125
Brain - Hippocampus: 0.8
Brain - Hypothalamus: 0.964285714286
Brain - Nucleus accumbens (basal ganglia): 0.705882352941
Brain - Putamen (basal ganglia): 0.344827586207
Brain - Spinal cord (cervical c-1): 0.928571428571
Brain - Substantia nigra: 0.666666666667
Breast - Mammary Tissue: 0.823529411765
Cells - EBV-transformed lymphocytes: 1.0
Cells - Transformed fibroblasts: 1.0
Cervix - Ectocervix: 1.0
Cervix - Endocervix: 0.0
Colon - Sigmoid: 0.725
Colon - Transverse: 0.796875
Esophagus - Gastroesophageal Junction: 0.509803921569
Esophagus - Mucosa: 1.0
Esophagus - Muscularis: 0.876543209877
Fallopian Tube: 0.5
Heart - Atrial Appendage: 0.98275862069
Heart - Left Ventricle: 1.0
Kidney - Cortex: 1.0
Liver: 1.0
Lung: 1.0
Minor Salivary Gland: 1.0
Muscle - Skeletal: 1.0
Nerve - Tibial: 1.0
Ovary: 1.0
Pancreas: 1.0
Pituitary: 1.0
Prostate: 1.0
Skin - Not Sun Exposed (Suprapubic): 0.807692307692
Skin - Sun Exposed (Lower leg): 0.925619834711
Small Intestine - Terminal Ileum: 0.96
Spleen: 1.0
Stomach: 0.903225806452
Testis: 1.0
Thyroid: 1.0
Uterus: 0.95
Vagina: 0.909090909091
Whole Blood: 1.0

コードまとめ

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import LabelEncoder
from sklearn.cross_validation import train_test_split
from sklearn.base import TransformerMixin
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier

### read gene expression matrix
usecols = [0] + list(range(2,8557))
df1 = pd.read_csv('GTEx_Analysis_v6p_RNA-seq_RNA-SeQCv1.1.8_gene_rpkm.gct', sep='\t', skiprows=2, usecols=usecols, index_col=0)
df1pc = df1 + 1
df1log = np.log2(df1pc)

### plot gene expression profiles
random_cols = np.random.choice(8555, 10)
df1log.iloc[:, random_cols].plot.density(fontsize=10)
plt.savefig('gtex_log_rpkm_density_random10sample.png', dpi=150)
#plt.show()

### read class labels
usecols = [0, 6]
df2 = pd.read_csv('GTEx_Data_V6_Annotations_SampleAttributesDS.txt', sep='\t', usecols=usecols, index_col=0)

### attach class labels
df = pd.concat([df1log.T, df2], axis=1, join_axes=[df1log.T.index])

### convert string labels
class_le = LabelEncoder()
label = class_le.fit_transform(df['SMTSD'].values)
label_r = class_le.inverse_transform(label)
df['SMTSD'] = label

### split into training and test data
smtsd_index = len(df.columns) - 1
X, y = df.iloc[:, :smtsd_index].values, df.iloc[:, smtsd_index].values
X_train, X_test, y_train, y_test = \
   train_test_split(X, y, test_size=0.3, random_state=0)

### save memory usage
del df
del df1
del df1pc
del df1log
del df2

### feature selection based on gene expression values
class GexSumFS(TransformerMixin):
    """
    Feature selection based on the sum of gene expression values
    """

    def __init__(self, sum):
        self.sum = sum

    def fit(self, X, y=None):
        self.indices_ = np.where(np.sum(X, axis=0) > self.sum)[0]
        return self

    def transform(self, X, y=None):
        return X[:, self.indices_]

sumfs = GexSumFS(sum = 500)
X_train_sumfs = sumfs.fit_transform(X_train)
X_test_sumfs = sumfs.transform(X_test)

### quantile normalization
class QuantileNormalization(TransformerMixin):
    """
    Quantile normalization
    """

    def __init__(self):
        pass

    def fit(self, X, y=None):
        self.ref_dist_ = np.zeros(X.shape[1])
        X_rank = pd.DataFrame(X).rank(axis=1, method='min').astype(int)
        for i in range(X.shape[1]):
            indices = np.where(X_rank == i+1)
            if len(indices[0]) > 0:
                self.ref_dist_[i] = np.mean(X[indices])
            else:
                self.ref_dist_[i] = self.ref_dist_[i-1]
        return self

    def transform(self, X, y=None):
        X_norm = pd.DataFrame(X).rank(axis=1, method='min').values
        for i in range(X.shape[1]):
            X_norm[X_norm == i+1] = self.ref_dist_[i]
        return X_norm

q_norm = QuantileNormalization()
X_train_sumfs_qnorm = q_norm.fit_transform(X_train_sumfs)
X_test_sumfs_qnorm = q_norm.transform(X_test_sumfs)

random_rows = np.random.choice(range(X_train_sumfs_qnorm.shape[0]), 10)
pd.DataFrame(X_train_sumfs_qnorm[random_rows, :]).T.plot.density(fontsize=10)
plt.savefig('gtex_qnorm_density_random10sample.png', dpi=150)
#plt.show()

### feature selection based on gene expression variance
from sklearn.base import TransformerMixin
import numpy as np

class GexVarFS(TransformerMixin):
    """
    Feature selection based on the variance of gene expression values
    """

    def __init__(self, var):
        self.var = var

    def fit(self, X, y=None):
        self.indices_ = np.where(np.var(X, axis=0) > self.var)[0]
        return self

    def transform(self, X, y=None):
        return X[:, self.indices_]

varfs = GexVarFS(var = 1)
X_train_sumfs_qnorm_varfs = varfs.fit_transform(X_train_sumfs_qnorm)
X_test_sumfs_qnorm_varfs = varfs.transform(X_test_sumfs_qnorm)

### standardization
stdsc = StandardScaler()
X_train_sumfs_qnorm_varfs_std = stdsc.fit_transform(X_train_sumfs_qnorm_varfs)
X_test_sumfs_qnorm_varfs_std = stdsc.transform(X_test_sumfs_qnorm_varfs)

### learning and prediction
knn = KNeighborsClassifier(n_neighbors=3, n_jobs=4)
knn.fit(X_train_sumfs_qnorm_varfs_std, y_train)
print('Training accuracy: ', knn.score(X_train_sumfs_qnorm_varfs_std, y_train))
print('Test accuracy: ', knn.score(X_test_sumfs_qnorm_varfs_std, y_test))

### accuracy score for each class
y_pred = knn.predict(X_test_sumfs_qnorm_varfs_std)
inv_dict = dict(zip(y, class_le.inverse_transform(y)))
for i in np.unique(label):
    accuracy_score = np.sum((y_pred[y_test == i] == i).astype(int)) / len(y_pred[y_test == i])
    print(inv_dict[i] + ': ' + str(accuracy_score))
29
22
1

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
29
22