#集合ってなに？#
基本情報でも出題があるのでせっかくだからまとめてみました。
ここやほかの解説サイトで学んで、試験の過去問等で演習をするといいと思います。
##集合の定義から##
集合はモノの集まりである。実はそれだけなんです。
ただし、いくつか約束があります。
####約束####
1 何も入っていない集合もあり。（空集合っていわれます。よく、$\phi$という記号で書かれます。）
2 入っているとか入っていないとかははっきりします。(入るかどうか微妙なものは扱わないです。)
この2つは約束してください。
###集合の例###
集合の例をここで考えてみましょう。
####例1. 偶数の集合####
{2, 4, 6, 8, 10, .... }
この集合には2や4といった偶数が入っています。偶数はすべてはいっています。22222222みたいな大きな数字でも、偶数なので入っています。
####例2. アルファベット文字列の集合####
{a, adg, ekls, sspkt, c, dh, lls,...}
次の例は数字ではありません。アルファベットの文字列の集合です。ちなみに、なぜアルファベットに限定したかというと、約束の2がはっきりとするからです。たとえば、"a,b,c"はアルファベットなので集合に入ります。しかし、"あ、か、せ"はアルファベットじゃないので入りません。
####例3. アルファベット3文字列####
{apk, ukg, adg, lls, usg,...}
つぎは例2の限定的な場合です。例2は何文字の列でも集合に入ります。例3は3文字のみしか集合に入りません。なので、例2で出てきた、"a, sspkt, c"とかは入りません。
####例4. 平均気温が20℃以上の日####
{過去の年月日とその日の平均気温T| T > 20℃}
つぎの例は集合を条件で書いています。Tは小数点まで考えたらきりがなく、こうやって条件で書いた方がいいです。
ちなみに例1を条件で書くと
{アルファベットn文字列 | n > 0}
です。ただ、これは文字列の数なので小数点とかはないですが。
ここで、書き方について追加の説明です。いちいち、上の例で出てきたような集合の中身を{}で囲って書くのは面倒くさいので、大文字のアルファベットで集合を表します。
だから、例1の場合は
A = {2, 4, 6, 8, 10, .... }
と約束したら、Aはその例1の集合を表します。もちろん、文字のダブりとかはないようにしていきます。数学の世界ではつぎの暗黙の了解があります。(本で書くときはたいてい断っていますが、やくそくなしに通じると思います。)なので、ここでは使わないようにします。
##集合の包含関係##
集合には包まれるとか堤とか考えることが出来ます。それを包含関係といいます。
2つの集合A,Bを考えます。Aの中身はすべてBの中身になっているとき、AはBに包まれるといいます。
数式で書くと
A\subset{B}
です。
イメージは上の図ですね。
ちなみに、例3の集合は例2の集合に包まれることがいえます。
##集合の共通部分と和と排他的論理和##
つぎは集合の和と共通部分ともう一つ、高校数学では扱っていない排他的論理和を考えます。
###共通部分###
式で書くと
A\cap{B}
とか
$$A\cdot B$$
って書きます。
イメージは上の図の赤い部分ですね。
例えば基本情報技術者試験は午前試験と午後試験があります。(非公式には0次試験という早起きをして会場にたどり着くというものもありますが。。。)
午前試験の合格者の集合がAとしましょう。午後試験の合格者をBとしましょう。両方の合格者が上の赤い部分に入ります。
###和###
式で書くと
A\cup{B}
とか
$$A+B$$
です。
例えば、基本情報を持っている人の集合をAとしましょう。そして、ファイナンシャルプランナーを持っている人の集合をBとしましょう。和はどちらか一方でも持っている人ということになります。ここで重要なのは、両方持っているひともカウントしています。そして、2重にカウントしないことです。
##排他的論理和##
つぎは排他的論理和です。これは、情報処理の勉強をして初めてでてきました。高校数学でも見たことがありません。こんども基本情報を持っている人の集合をAとしましょう。そして、ファイナンシャルプランナーを持っている人の集合をBとしましょう。このとき、両方持っている人は考えません。片方だけ持っているひとの集合です。
式は
$$A\oplus B$$
です。
##否定##
次は否定です。
否定は集合の外側です。基本情報を持っているひとの集合の場合、否定は持っていない人の集合です。ちなみに、外側とはどこまで考えればいいのでしょうか？まあ、たいていは前提となる集合がはっきりしています。それを背景集合といいます。
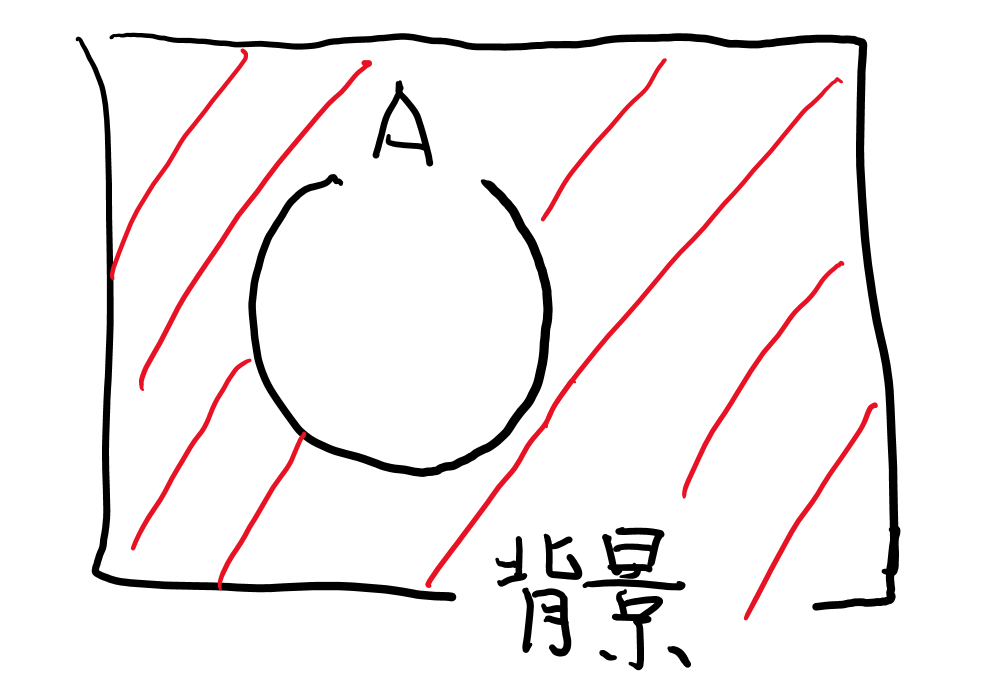基本情報の例の場合、国内の人とか会社の人とかが背景に当たります。
##ド・モルガンの法則##
```math
\overline{A\cup{B}}=\overline{A}\cap{\overline{B}}\\
\overline{A\cap{B}}=\overline{A}\cup{\overline{B}}
```
という公式が成立します。
ちなみに、たくさんの集合が並んでいてもOKです。
\overline{A_{1}\cup{A_{2}}\cup{A_{3}}\cup{A_{4}}...\cup{A_{100}}}=\overline{A_{1}}\cap{\overline{A_{2}}\cap{\overline{A_{3}}...\overline{\cap{A_{100}}}}}\\
\overline{A_{1}\cap{A_{2}}\cap{A_{3}}\cap{A_{4}}...\cap{A_{100}}}=\overline{A_{1}}\cup{\overline{A_{2}}\cup{\overline{A_{3}}...\overline{\cup{A_{100}}}}}
これは、集合と対で必要になる論理の部分で重要になります。
ちなみに数学的な解説はほかのサイトに譲ります。
次のサイトが丁寧でいいです。
高校数学の美しい物語
https://mathtrain.jp/de
#最後に#
##この記事はあくまで練習である##
内容に入るまえにこの記事を書く動機について説明をしていきたい。
多分、このジャンルの記事を書く人は少ないと思う。また、需要もそんなにないと思う。
しかし、この投稿は実は私の初投稿なのである。だから、投稿の要領を掴むためにこんなジャンルの記事を書いてみた。だから、あくまで、参考程度で読んでほしい。