動機
とある数値計算のコードを書いていた際に、二つの楕円同士の衝突、すなわち
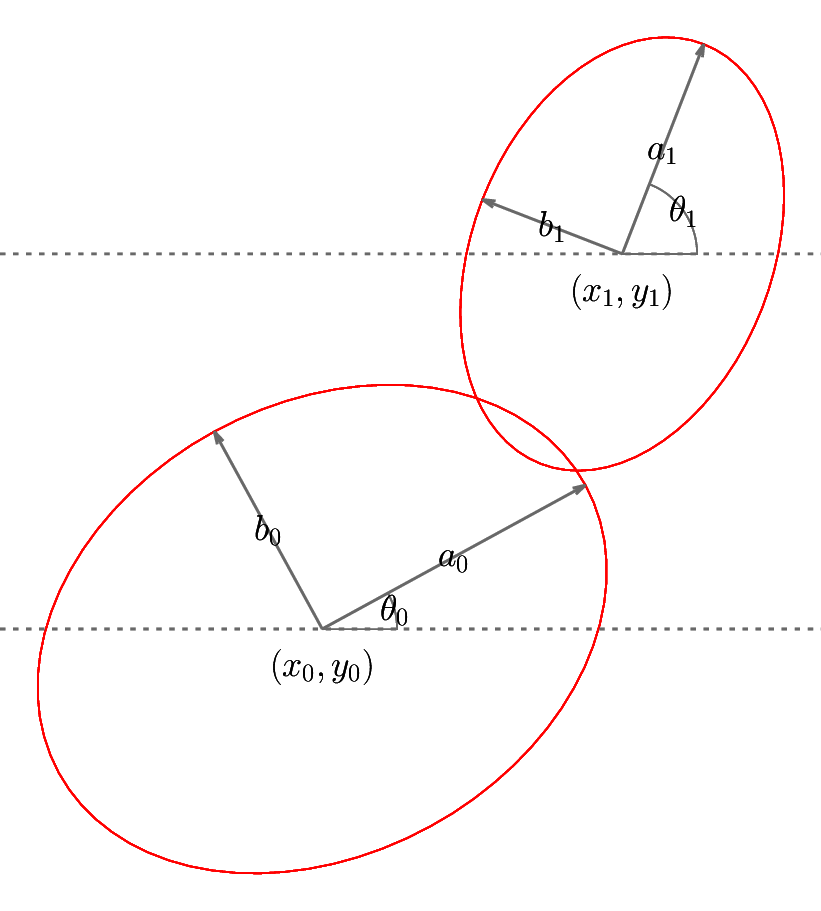
この図のような状況で、
- そもそも重なっているのか
- 重なっているならどの程度か(以下では便宜上衝突量と呼びます)
を調べる必要がありました。
変形は一切しないものとし、とある理由(最後に記述)で衝突量は楕円の大きさに比べて小さいと仮定します。
円同士の衝突判定に比べて情報が少なかったので自分なりに試行錯誤しましたが、まあこんなものかなと思った案の一つを書き残しておきます。
以下の話はとある数値計算において「それっぽい」結果を得るための近似解なので、数学的に厳密ではないこと、また適用範囲も限られることをご留意ください。
素人考えですがゲームなどでの衝突判定として一応適用可能だとおもいます。
TL;DR
楕円の一部を円で近似して円同士の衝突問題に変換することで、衝突の判定と定量化を簡単に扱います。
問題設定と課題
問題設定
中心点が原点で長軸$a$短軸$b$の傾いていない楕円上の点$(x_e, y_e)$(eはellipseのつもりです)は
\frac{x_e^2}{a^2}
+
\frac{y_e^2}{b^2}
=
1
で表されます。簡単のため媒介変数$t$を導入すると
\begin{pmatrix}
x_e \\
y_e
\end{pmatrix}
=
\begin{pmatrix}
a \cos t \\
b \sin t
\end{pmatrix}
となります。一般には楕円は傾いていて(角度を$\theta$とします)、中心$( x_0, y_0 )$も原点ではないので、
\begin{pmatrix}
x_e \\
y_e
\end{pmatrix}
=
\begin{pmatrix}
x_0 \\
y_0
\end{pmatrix}
+
\begin{pmatrix}
\cos \theta & - \sin \theta \\
\sin \theta & \cos \theta
\end{pmatrix}
\begin{pmatrix}
a \cos t \\
b \sin t
\end{pmatrix}
となるでしょう。もう一つの楕円に対しても全く同じ式が得られます。
普通に捉えれば楕円の衝突問題はこれら二つの楕円の交点を求める問題に帰着しますので、導いた二式を連立して解けば万事解決です。真面目に頑張って計算すると、円同士の場合$x_e$か$y_e$についての二次方程式に帰着するところ、楕円同士では一般的には四次方程式になります。四つ実数解があれば二つの楕円が四点で交わり、二つが実数解で残りが虚数解の場合二点で交わり、さらにはその実数解が重解であれば丁度一点で衝突、全て虚数解だと交点なし、などなどです。
課題
四次方程式には有名な解の公式が存在しますが、虚数や立方根が含まれていて結構大変です。数値的に扱うと数値誤差でNaNになる、といったことが頻発しますので、きちんと場合分けをする必要が出てきます。
また仮に厳密解(すなわち交点)が求まったとしても、衝突量は一意に定まりません。衝突している場合は一番はじめの図のようになりますが、どこからどこまでの長さをもって衝突量とするのかは結構曖昧です。
したがって今回は近似を許容してより簡便な方法を考えることにしました。
注意
上では傾いていたり中心が原点になかったりといった一般的なケースを考えましたが、そのまま扱うと議論が面倒ですので、任意の点$(x_p, y_p)$(pはpointのつもりです)と楕円との関係を考える場合は座標変換
\begin{pmatrix}
x_p \\
y_p
\end{pmatrix}
\leftarrow
\begin{pmatrix}
\cos ( -\theta) & - \sin ( -\theta) \\
\sin ( -\theta) & \cos ( -\theta)
\end{pmatrix}
\begin{pmatrix}
x_p-x_0 \\
y_p-y_0
\end{pmatrix}
しておく(原点へ並進移動の後$-\theta$だけ回転移動)こととし、この系の座標$( x_p, y_p )$を元の座標系に戻したい時には逆変換
\begin{pmatrix}
x_p \\
y_p
\end{pmatrix}
\leftarrow
\begin{pmatrix}
x_0 \\
y_0
\end{pmatrix}
+
\begin{pmatrix}
\cos \theta & - \sin \theta \\
\sin \theta & \cos \theta
\end{pmatrix}
\begin{pmatrix}
x_p \\
y_p
\end{pmatrix}
を行う($+\theta$だけ回転移動の後元の中心へ並進移動)こととします。
これにより以下の議論では楕円のうちの一つは原点中心にあって傾いていないと仮定できます。
円による近似
楕円同士の衝突は面倒ですが、円同士の衝突は比較的簡単に扱うことができ、二つの円(半径が$r_0$と$r_i$で中心間の距離が$d$)に対する衝突量$\delta$は例えば
\delta = r_0 + r_1 - d
と定義でき、この量が正なら二つの円は重なっている、負なら離れていると判断できます。
さらに今回ははじめに述べた通り、衝突量は楕円の大きさに比べて小さいことを仮定しています。
したがって一部分を円で近似して、円同士の衝突として扱ってしまおう、というのがここでの基本的な考え方です。
ありがたいことに楕円の一部を近似する円の中心と曲率には理論式が存在し、円の中心$( x_c, y_c )$は媒介変数$t$(これは楕円を表現したのと同じ媒介変数)を変数として
\left\{
\begin{matrix}
x_c = a \left( 1 - \frac{b^2}{a^2} \right) \cos^3 t, \\
y_c = b \left( 1 - \frac{a^2}{b^2} \right) \sin^3 t
\end{matrix}
\right.
で、その曲率は
\frac{
a b
}{
\sqrt{\left( a^2 \sin^2 t + b^2 \cos^2 t \right)^3}
}
で与えられます(半径はこの逆数)。
残る問題は、任意の点$(x_p, y_p)$から楕円を見た時にいい感じの近似円を与えてくれる$t$をどのようにして求めるか、です。
点と楕円の最短距離
上述の方法で楕円の一部を円で近似する場合、両者の法線(および接線)ベクトルは一致します。
直感的には微小部分に着目すると二本の曲線が重なるという意味です。
この法線ベクトル上に近似円の中心$(x_c, y_c)$、楕円との交点、任意の点$(x_p, y_p)$の三点が並ぶような状況というのは、実は点$(x_p, y_p)$から楕円への最短距離を求める問題に帰着します。
したがって上で提起した問題は、点$(x_p, y_p)$への最短距離を求める問題と捉えることができます。
点と楕円の最短距離を求める手法としては、こちらのページを大いに参考にさせていただきました、というか言語だけ変えてそのまま使用しています。
ざっくり言えば$t$をうまいこと調節して$( x_c, y_c )$と$( x_p, y_p )$を結んだ線分を近似円に直交させています。
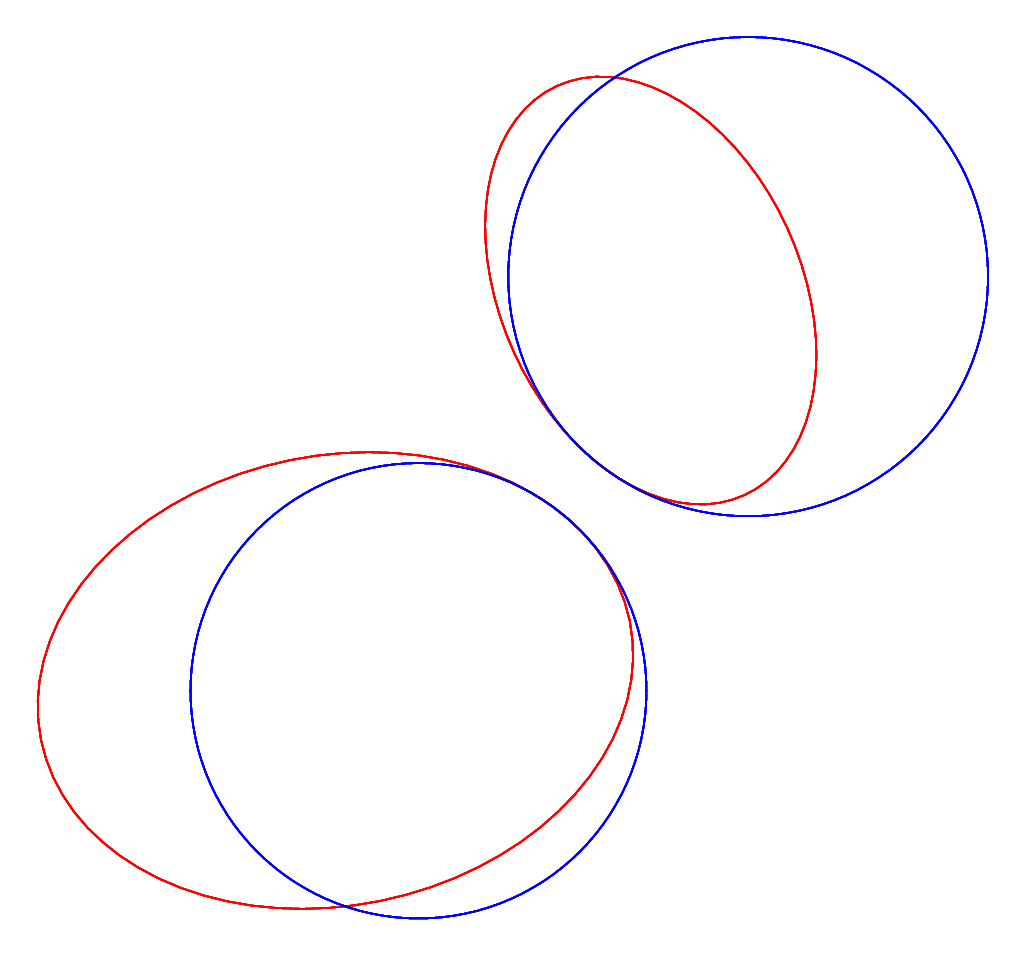
実際にフィッティングしてみると以下の図のようになります。点$(x_c, y_c)$と点$(x_p, y_p)$を結んだ黒矢印がおおよそ赤い楕円や青い円と直交している様子、および青い円が交点周辺で楕円の良い近似になっている様子が見てとれるかと思います。

直接解法ではなくiterativeな手法ですが、触ってみた感じ大体3から4回で収束しますし、何より安定しているのが好印象です。
極端に歪んだ楕円の内側の判定は若干挙動が怪しいことがありますが、幸い今回対象とする点は外側に存在するので問題ありません。
衝突判定
衝突判定にはこの手法を応用しています。
応用といっても非常に単純で、衝突相手の近似円の中心$(x_c, y_c)$を互いに$( x_p, y_p )$とみなし、最短距離を求めるプロセスを収束するまで繰り返しているだけです。
二物体が衝突していれば下の図のようになります。

衝突していない場合下の図のようになります。
最終的に得られる二つの近似円から衝突量$\delta$を上で述べたように定義し、衝突判定と定量化を行なっています。
Iterate(点と楕円の最短距離)の上からiterate(二つの近似円の調整)するのが少々気に入らないですが、流体計算では他の箇所のコストがもっと高いため目立ちません。
なお一方の楕円が他方に完全に含まれるようなケースでは明らかに破綻しますが、始めに述べた通り今回は割り切って考慮していません。
実装
コードはこちらにおいてあります。
応用例
埋め込み境界法と有限差分法を組み合わせた流体構造連成のシミュレーションへ応用した例です。
詳細は割愛しますが流体を考える上では一般的な手法を用いています。
表面は理想的に滑らかという仮定なので理論上粒子は接触し得ないのですが、現実的な解像度では適切な衝突モデルを用いないと物体同士がお互いに貫入し過ぎる非物理的な現象が発生します。
これを防いでそれっぽい解を得るために、粒子間に本記事で取り上げた衝突量$\delta$に比例した反発力を加えています。
流体や物体は時間方向に十分小さい刻み$\Delta t$で更新しているため、離散時間$n$において衝突処理がきちんと行われていれば次の離散時間$n+1$においての衝突量は非常に小さいことが予測されます。
これがはじめに衝突量が小さいことを仮定し、円での近似が妥当であると考えた理由です。
流体ソルバはこちらです。