TL;DR
- 勾配法はほとんどのケースで極小点に収束する(鞍点には収束しない)
- この事実は力学系や最適化の分野ではよく知られているが,機械学習では新しい?
- 数年前にバズった勾配法の比較動画は実際の学習現象を説明できていないかも
- 鞍点の近傍での振舞いで差がつく? いや,そもそも鞍点近傍に流れ込まないかも
- 比較動画に登場した鞍点は,実際にはまず生じないタイプかも
- 機械学習にも役立つモース理論
- ほとんどすべての関数はモース関数
- モース関数の臨界点のタイプはわずか $d+1$ 種類($d$ は定義域次元)
- 安定/不安定多様体とモース・スメール複体で勾配法の流れは分かる
- Monkey saddleはまず現れない(もし現れても簡単に消せる)
- 量的な問題に関しては,結局は実験するしかない
この記事を書いたきっかけ
昨夜,ある論文を見かけて,ふとこんなツイートをした.
深夜2:30のツイートなのでスルーされると思っていたら,TJOさんにリツイートされてバズった.有名ツイッタラー恐るべし…ML業界,「勾配法が鞍点に収束する確率はゼロ」という論文が2016年にトップ会議に通ってたりして,分野の壁は厚いなと感じることがある.
— はま (@hmkz_) 2018年2月10日
当該の論文はこれ.
「自分野では周知の知識が他分野では未知」というのはよくあることなので,別にそれ自体は悪いことではないし,本当に未知なら早く広まったほうがいい大切な知識だとは思うけど,MLerって最適化強い人多い印象だったから意外感はある.https://t.co/3nvnXNz06V
— はま (@hmkz_) 2018年2月10日
論文はCOLT2016に採録されている.非MLer向けに補足すると,COLTというのは機械学習の理論系国際会議.機械学習の国際会議というと世間的にはNIPS, ICML, AAAI, IJCAIあたりが有名だと思うけど,COLTはそれらに勝るとも劣らないトップ会議の1つである.そのわりに知名度が低い理由は,上記ML四天王に輪をかけて理論寄りなため,ビジネスパーソンには近寄り難いせいかもしれない(偏見).ちなみに僕は通したことがない(投稿したこともないけど).
論文は,以下のことを示している.
2階連続微分可能な関数 $f:\mathbb R^d \to \mathbb R$ の各臨界点($\nabla f(x)=0$ をみたす点 $x\in \mathbb R^d$)が極小点(近傍に自身より値が小さい点が存在しない)か狭義の鞍点($\nabla^2 f(x)$ が負の固有値をもつ)のいずれかであるならば,ランダムに選んだ初期点 $x_0 \in \mathbb R^d$ からスタートした勾配法$$x_{k+1} = x_k - \alpha \nabla f(x_k)$$は $\alpha$ を十分小さくとれば,ほとんど確実に極小点に収束する(言い換えれば,鞍点に収束する確率はゼロ).
証明には,安定多様体(後述)の概念が使われている.
さて,この定理や安定多様体を使った証明は,大学で力学系や最適化を専攻した人にとっては半世紀以上前から知られる常識的な話だと思う. [2018/02/13 訂正] 有限のステップサイズで解析した点は新規だと思う.無限小ステップサイズのときには現れない非自明な議論もされている.Stephen Smale. Differentiable dynamical systems. Bulletin of the American mathematical Society, 73(6): 747–817, 1967 などを引用しており,無限小ステップサイズでの議論が既知であることは著者も認識している. とはいえ,そういった細かい部分を無視すれば,大体はモース理論の周辺の話だ.もちろん,他分野ですでに常識だから価値がないとか,どちらの分野が優れているというつもりはない.全分野に精通した人はいないし,他分野の常識を知らないのはお互い様.むしろ,もし本当にこういう大切な知識が知れ渡っていないなら,周知のためにも積極的にトップ会議に採録されたほうがいいと思う.
僕は最適化(進化計算)の研究者なので,機械学習コミュニティにとってこの論文がどの程度新規性のある内容だったのか,細かい機微は分からない.しかし,もし知らない人が少なからずいるなら,このあたりの知識は機械学習にも役立つはずなので知っておいて損はないと思う.そこで昨晩の連ツイに絡めて,関連するモース理論の概念を紹介する.
ほとんどすべての関数はモース関数
以下,この記事で考える関数は2階連続微分可能,つまり各点において以下の勾配とヘッセ行列が存在して,それらは $y$ について連続関数であるとする.
(定義)
関数 $f:\mathbb R^d\to\mathbb R$ に対して,1階導関数を並べたベクトル
$$\nabla f(y):=\left(\frac{\partial f}{\partial x_1}(y),\dots,\frac{\partial f}{\partial x_d}(y)\right)^t$$を 勾配 (gradient) といい,2階導関数を並べた行列
\nabla^2f(y):=
\begin{pmatrix}
\dfrac{\partial^2 f}{\partial x_1 \partial x_1}(y) & \cdots & \dfrac{\partial^2 f}{\partial x_1 \partial x_d}(y)\\
\vdots & \ddots & \vdots\\
\dfrac{\partial^2 f}{\partial x_d \partial x_1}(y) & \cdots & \dfrac{\partial^2 f}{\partial x_d \partial x_d}(y)
\end{pmatrix}
を へッセ行列 (Hessian matrix) という.
勾配法が止まるのは,微分が消えるところ.そのような点を臨界点という.
(定義)
関数 $f:\mathbb R^d\to\mathbb R$ に対して,点 $x\in\mathbb R^d$ が $\nabla f(x)=0$ をみたすとき, $x$ を 臨界点 (critical point) といい, さもなければ 正則点 (regular point) という.点 $v\in\mathbb R$ の逆像 $f^{-1}(v):=\{x\in\mathbb R^d\mid f(x)=v\}$ が臨界点を含むとき, $v$ を 臨界値 (critical value) といい,さもなければ 正則値 (regular value) という.
モース理論では,臨界点の近傍の形状がヘッセ行列で表せるような関数を扱う.
(定義)
関数 $f:\mathbb R^d\to\mathbb R$ が モース関数 (Morse function) とは, $f$ のすべての臨界点が非退化であり,異なる臨界値をもつことをいう.ここで,臨界点 $x\in\mathbb R^d$ が 非退化 (nondegenerate) とは, ヘッセ行列 $\nabla^2f(x)$ が正則すなわち $\text{rank } \nabla^2f(x)=d$ であることをいう.
「ヘッセ行列が非退化」というのは一見強い仮定をおいたようにもみえるが,実際はほとんどすべての関数はモース関数になっている.
(定理)
2階連続微分可能な関数 $f:\mathbb R^d\to\mathbb R$ 全体の集合を $C^2(\mathbb R^d,\mathbb R)$ で表す.この空間の点(関数!) $f$ の開近傍を任意の $\varepsilon \in C^2(\mathbb R^d, \mathbb R_+)$ について
\begin{align}
N(f,\varepsilon)&=\left\{g\in C^2(\mathbb R^d,\mathbb R)\ \right|\\
&\qquad \left. \forall x\in \mathbb R^d: \|f(x)-g(x)\| + \|\nabla f(x)-\nabla g(x)\| + \|\nabla^2f(x)-\nabla^2g(x)\| < \varepsilon(x)\right\}
\end{align}
で定義する1.このとき,モース関数全体の集合は $C^2(\mathbb R^d,\mathbb R)$ の稠密開集合をなす.
「稠密開集合をなす」というのは,「ほとんど至る所」を一般化した概念と捉えてほしい.つまり,ほとんどすべての関数はモース関数だし,モース関数でない関数はモース関数によって任意の精度で近似できる.しかも単に関数値が近いというだけでなく,その勾配やヘッセ行列までが近いように近似できる.
モース関数の臨界点のタイプはわずか d+1 種類
次のモースの補題により,モース関数の臨界点の近傍の形状は,適切な座標変換を施せば簡単な標準形で表せることがわかる.
(定理)
モース関数 $f:\mathbb R^d\to\mathbb R$ の原点 0 が臨界点であるとする.このとき,ある座標変換(微分同相写像) $\phi:\mathbb R^d\to\mathbb R^d$ が存在して,以下のように表せる:
$$
f\circ\phi(x) = - x_1^2 - x_2^2 - \dots - x_{\lambda}^2 + x_{\lambda+1}^2 + \dots + x_d^2.
$$
この $\lambda$ は座標変換の取り方によらない.これを臨界点の 指数 (index) という.
証明は,ヘッセ行列を対角化したとき,負の固有値の重複度も込めた個数が指数に一致することを使って示すことができる.詳しくは松本 (1997)などを参照.
つまり,モース関数の臨界点の近傍での形状は,「ある方向には上に凸な関数で,別の方向には下に凸な関数」というものだ.指数はいくつの方向に対して上に凸であるかを決めている.指数は $\lambda=0,\dots,d$ までの $d+1$ 通りの値をとる.したがって,モース関数にはわずか $d+1$ 種類の臨界点しか生じないことがわかる. $\lambda=0$ は極小点, $\lambda=d$ は極大点,それ以外は鞍点とよばれる.
安定/不安定多様体とモース・スメール複体で勾配法の流れは分かる
さて,一般的な関数が以上のような性質をもつことをふまえて,連ツイの問題を考えてみる.
深層学習erも「深層学習では損失関数の臨界点の大半は鞍点.だから鞍点の近傍での学習の振舞いで差がつく」といって色々な勾配法を提案してる.いくら鞍点が多いといっても高々有限個だし,勾配法が鞍点の近傍に流れ込む確率なんてほとんど無視できる気がするんだけど,何か特別な理由があるんだろか?
— はま (@hmkz_) 2018年2月10日
勾配法の違いの説明でよく見るこの画像.すごく分かった気にさせてくれるんだけど,本当に実際の学習でこんなこと起こってるん?「実データを使った深層学習で,勾配法が実際にこういう挙動をしたことを観測した」という論文があったら教えてほしい.https://t.co/hChgL65HoK
— はま (@hmkz_) 2018年2月10日
様々な勾配法の鞍点近傍での挙動を比較する図が流行った.たしかに鞍点近傍ではかなり差がつくようだ.問題は,果たして勾配法が鞍点近傍に流れ込むことがそんなに頻繁にあるのかということだ.
ステップサイズ無限小での勾配法の軌跡を考える.
(定義)
曲線 $x:\mathbb R\to\mathbb R^d$ で $$\frac{\partial}{\partial t}x(t) = -\nabla f(x(t))$$ をみたすものを 積分曲線 (integral curve) という.
積分曲線の終点は勾配の消える点,すなわち臨界点になる.いろいろな初期点からスタートした積分曲線がどこに流れ込むかを考えてみる.
(定義)
積分曲線 $x:\mathbb R\to\mathbb R^d$ と臨界点 $p\in\mathbb R^d$ について,$$S(p)=\{p\}\cup\{x_0\in\mathbb R^d\ |\ x_0\in\text{Im } x,\ \lim_{t\to+\infty}x(t)=p\}$$を 安定多様体 (stable manifold) といい,$$U(p)=\{p\}\cup\{x_0\in\mathbb R^d\ |\ x_0\in\text{Im } x,\ \lim_{t\to-\infty}x(t)=p\}$$を 不安定多様体 (unstable manifold) という.
これらの多様体を使って,「どの初期点がどの臨界点に流れ込むか」を表した地図を作ることができる.
(定義)
任意の臨界点 $p,q\in\mathbb R^d$ について,安定多様体 $S(p)$ と不安定多様体 $U(q)$ は横断的に交わるとする(この仮定はほとんどの関数で成り立つ).このとき,$$C=\{S(p)\cap U(q)\ |\ p,q\in\mathbb R^d,\ p,q\text{ は臨界点}\}$$をモース・スメール複体という.この複体の要素を セル (cell) という.
 図: 2次元における (a) 不安定多様体,(b) 安定多様体,(c) モース・スメール複体,(d) 鞍点を繋いだ図(今回の議論には関係ない).臨界点は0次元セル,極大点から鞍点に向かうパスと鞍点から極小点に向かうパスが1次元セル,これらのパスに囲まれた極小点に収束する領域が2次元セルである.
出典: https://www.researchgate.net/figure/Morse-Smale-complex-a-Descending-manifolds-of-maxima-and-saddles-b-Ascending_fig10_6204492
図: 2次元における (a) 不安定多様体,(b) 安定多様体,(c) モース・スメール複体,(d) 鞍点を繋いだ図(今回の議論には関係ない).臨界点は0次元セル,極大点から鞍点に向かうパスと鞍点から極小点に向かうパスが1次元セル,これらのパスに囲まれた極小点に収束する領域が2次元セルである.
出典: https://www.researchgate.net/figure/Morse-Smale-complex-a-Descending-manifolds-of-maxima-and-saddles-b-Ascending_fig10_6204492
安定多様体と不安定多様体からモース・スメール複体が作られる様子は,このスライドの23ページからの図がわかりやすい.
このセル分割を用いて,以下のことが示せる(TODO:あとで出典追加).
(定理)
点 $p\in\mathbb R^d$ を指数 $\lambda$ の臨界点とする.積分曲線が $p$ に流れ込むセルは, $d-\lambda$ 次元である.
この定理からわかるように,鞍点に収束するような初期点を表すセルの次元は $d$ よりも真に小さい.したがって,それは測度 0 の領域で,つまり空間全体からみれば無視できるほど小さい.これを示していたのがCOLT論文だ.しかし積分曲線が「ピタリと鞍点に流れ着く」のではなく「鞍点近傍を通過する」ような初期点はならば,関数次第でそれなりにあるかもしれない.このあたりは量的な問題なので,モース理論だけからは分からない.臨界点がモース・スメール複体のセルの頂点に位置することを考えると,高次元の関数では,球面集中現象によってセルの体積の大半はカドに集中するはずだから,鞍点近傍を通過するケースというのも結構あるのかもしれないなと思った.
そんなわけで「ちょっとイキりすぎたかな」と反省していたところ,dhgrsさんにいいこと教えてもらった.
ちなみに,上記論文は[Blogにもなっている](http://www.offconvex.org/2017/07/19/saddle-efficiency/).こちらのほうが図が豊富で分かりやすいと思う.この論文によると,たとえ高次元になっても鞍点の近傍にはほとんど引き込まれないらしい.たしか鞍点近傍の振舞い比較が流行ったのが2014年頃だったと思うので,3年で認識が覆されたことになる.最近はAdamを鞍点近傍での停滞を避けるためではなく正則な領域での加速のために使うらしい.機械学習の進歩はすごい早さだ.少なくとも私が知っている範囲のDLだと、鞍点が原因で学習が停滞するというのは過去の考えで、最近はそれを否定する論文が多く出ている印象です。研究室slackで1番最近話題になったものだとこちら。https://t.co/J2zbCLlSvT https://t.co/Rc3nDA2naV
— dhgrs (@__dhgrs__) 2018年2月11日
「鞍点で学習が停滞」が過去のものになりつつある?例として、Adamはロス減少が早いが汎化能力が低いので、途中からSGDに変え汎化能力を上げるという論文があります。この背景には、「Adamは鞍点を避けるためではなく学習を早くするために使う」新常識があるかと思います。https://t.co/TwZxCkSdwh https://t.co/gws7sYeTiA
— dhgrs (@__dhgrs__) 2018年2月12日
Monkey saddleはまず現れない(もし現れても簡単に消せる)
モースの補題からわかるように,もう1つのツイートは正しいと思う.
3番目の画像というのはこれ.さっきのリンク先には3つの画像が上がってるんだけど,特に3番目の画像,これMonkey saddleじゃないの?
— はま (@hmkz_) 2018年2月10日
関数摂動したら消えるような臨界点が,実データを使った学習で生じるとは信じがたいんだけど…https://t.co/yjCDnImh0E
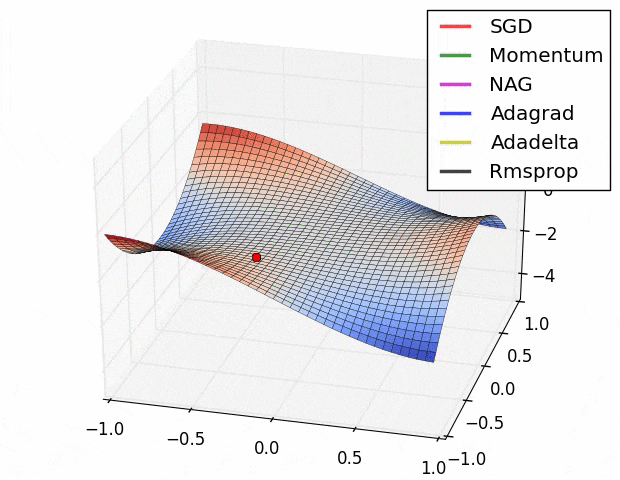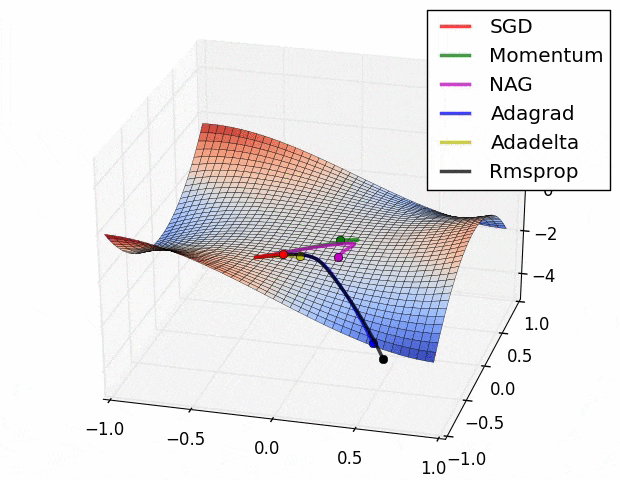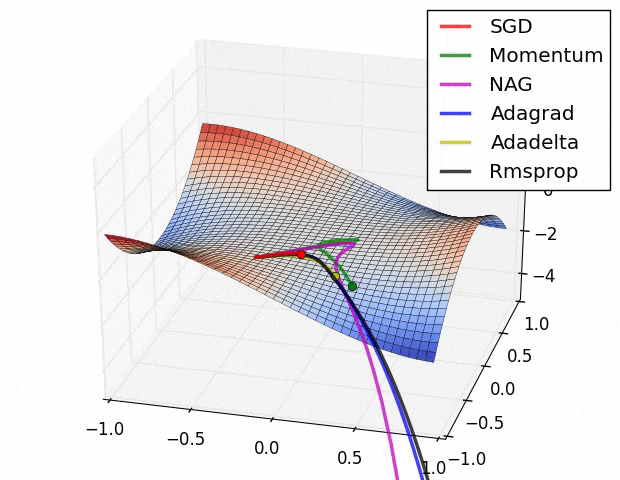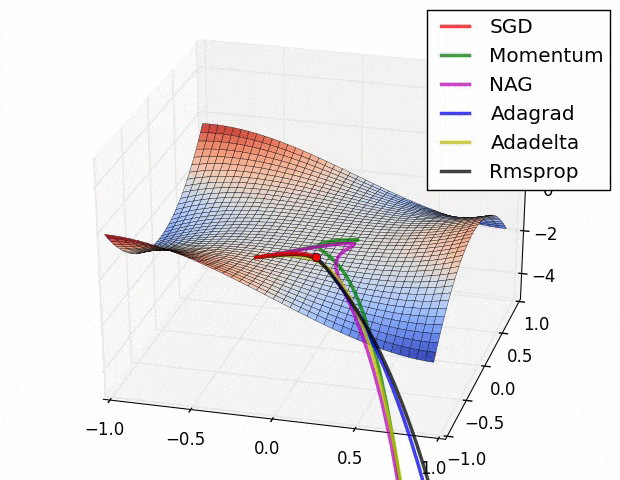 この図の原点 $(x,y,z)=(0,0,0)$ は[Monkey saddle](https://en.wikipedia.org/wiki/Monkey_saddle)という臨界点で,その周りでは関数は(適切な座標変換で標準形に直せば)
$$z=x^3-3xy^2$$
という形をしている.上式に2次の項が存在しないことからわかるように,この臨界点は退化している.退化した臨界点は関数を摂動すると消える.ちょうど3次関数 $f(x)=x^3$ の臨界点(変曲点) $x=0$ が摂動を加えて $f'(x)=x^3+\varepsilon x$ $(\varepsilon >0)$ とすると消えてしまうのと同様だ $(\nabla f'(x)=3x^2+\varepsilon \ne 0)$.
この図の原点 $(x,y,z)=(0,0,0)$ は[Monkey saddle](https://en.wikipedia.org/wiki/Monkey_saddle)という臨界点で,その周りでは関数は(適切な座標変換で標準形に直せば)
$$z=x^3-3xy^2$$
という形をしている.上式に2次の項が存在しないことからわかるように,この臨界点は退化している.退化した臨界点は関数を摂動すると消える.ちょうど3次関数 $f(x)=x^3$ の臨界点(変曲点) $x=0$ が摂動を加えて $f'(x)=x^3+\varepsilon x$ $(\varepsilon >0)$ とすると消えてしまうのと同様だ $(\nabla f'(x)=3x^2+\varepsilon \ne 0)$.
さて,上記ツイートの疑問は,このような退化臨界点が実データを使った学習において生じるのか?というもの.ないと言い切ることは難しい(悪魔の証明だ)が,現実的にはまずありえないだろうと思っている2.
ほかにも,学習プロセスにドロップアウトやモンテカルロ近似が含まれる場合など,損失関数は様々な理由で自然に摂動されている.だから,現実の問題で最適化することになる損失関数は,退化臨界点が消えたあとの関数(つまりモース関数)ではないかと思う.もし摂動が一切加わっていないと思われるケースに直面しても,なんなら小さな乱数を加えることで人為的に退化臨界点を消すこともできる.だからもし,退化した臨界点をもつ関数に出会ったら,何か特別なことがおこっているはず.実データにはノイズがつきものだし,そもそも学習時にミニバッチするしで,損失関数には必然的に摂動が加わっているはず.そういう状況でMonkey saddle(やその他の不安定特異点)が残るとは一般論としては思えない.逆に,もし残っているなら,何か特別な興味深い現象が起こっているはず.
— はま (@hmkz_) 2018年2月10日
量的問題に関しては,結局は実験するしかない
モース理論はかなり抽象的な理論なので,ある対象が存在するとかしないとか,質的な判断しかわからない.量的な問題は,具体的な式で解析するとか,実験するとかしないといけない.
もしこの記事に書いた内容が機械学習コミュニティで知られていないならインパクトはあるし,どちらに転んでも成果になるので,それなりにうまい話ではないかと思う.いずれにせよ,実データを使った学習で,先述の図のようなことが本当に観測できるのかどうかを確認することは大きな意義があると思う.観測できなければ迷信が取り払えるし,観測できれば新現象の発見につながる.誰かやってみませんか?
— はま (@hmkz_) 2018年2月10日
ちなみにシンギュラリティを広めるお仕事というのは例えば[これとか](https://qiita.com/NaokiHamada/items/020e18563c8616d4bb9a).今回の記事を多目的最適化に拡張した内容にあたるので,ぜひ読んでみてほしい.ちゃんとやればNIPS/ICML/COLTあたり狙えるネタだし,言い出しっぺの自分がやれという話だけど,いま僕はシンギュラリティを世に広めるお仕事に集中したいのであと5年は無理そうだ…
— はま (@hmkz_) 2018年2月10日