紹介する論文
論文の要約
- 機械学習(深層学習)を用いて自己位置推定の成功・失敗を学習して識別するが,機械学習による識別率が必ず100%になることはない
- 機械学習による成功・失敗の出力を新たな可観測変数として利用できると仮定し,自己位置推定とその推定結果の信頼度を同時推定する問題を定式化する
- 安直に機械学習の出力を用いて自己位置推定の正誤を判断するよりも,推定した「信頼度」が正しく自己位置推定の正誤を識別できる
はじめに
私自身が2018年に書いた論文です.
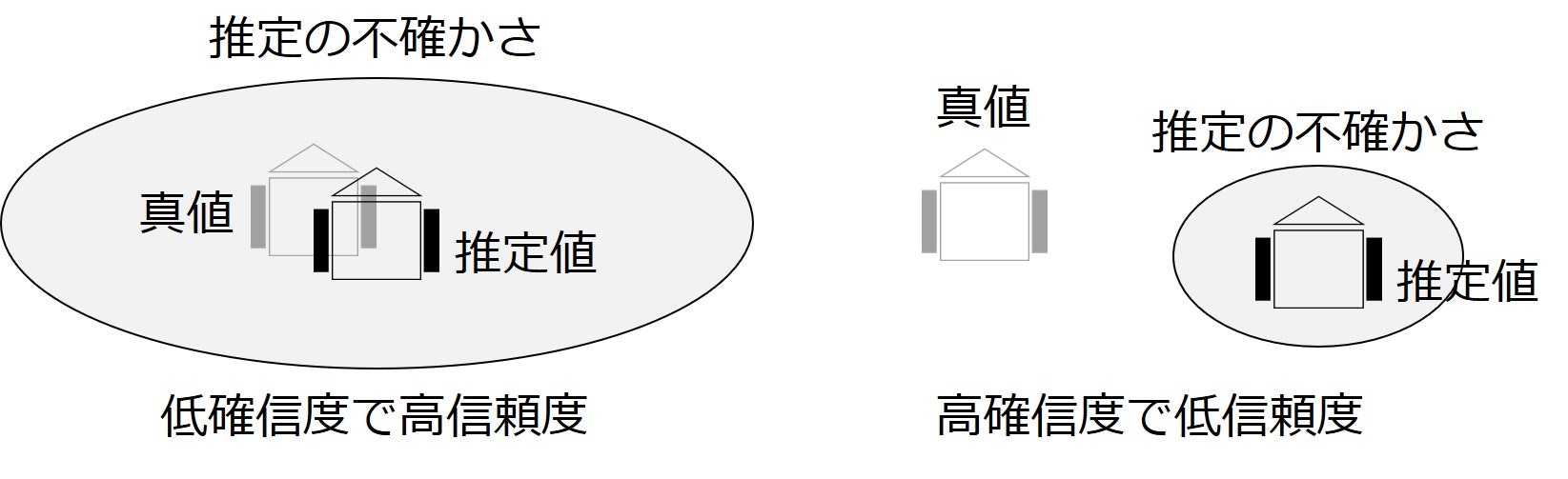
自己位置推定を確率的に解くと,自己位置に対する確率分布(例えばパーティクルフィルタを使えば,パーティクル群が確率分布を近似します)を得ることができます.確率分布を用いることで、推定結果の不確かさ(uncertainty)を得られます.この逆数を取った様な値が確信度(confidence)になります.すなわち,分布の裾が狭ければ推定結果に自信があり,裾が広ければ自身がないということになります.しかし確信度は,今回推定の目的とする信頼度(reliability)とは異なります.
例えば上図の左では,推定の不確かは大きいですが,推定値は真値に近い状態にあります.すなわち「確信度は低いが信頼度は高い」という状態になります.一方で右は,推定の不確かさは小さいが,推定値と真値が大きくずれている状態を表しています.すなわち「確信度は高いが信頼度は低い」という状態になります.この例からも,確信度と信頼度が違うものであることがわかると思います.
前述の通り,自己位置推定の問題を解いて得られるのは確信度のみなので,信頼度を得るためにはこれまでの方法論ではいけないことになります.そこで本研究では,新たに信頼度を推定するための問題の定式化を行います.
信頼度推定のモチベーション
自己位置推定は自動運転のためにも重要な技術であり,自己位置推定の失敗は自動運転の失敗にも直結し得ます.そして自動運転レベル3では,「機械が失敗しそうな場合には,機械は運転手に運転権限を委譲する」とあります.これはすなわち,「機械が自らの計算結果に対する信頼度を知る必要がある」ということを意味しています.しかし前述の通り,自己位置推定の問題を解いても,その推定結果に対する信頼度を得ることはできません.なので,「自己位置推定結果の信頼度を正しく予測したい」というモチベーションが出てきました.
深層学習を用いた自己位置推定の正誤判断
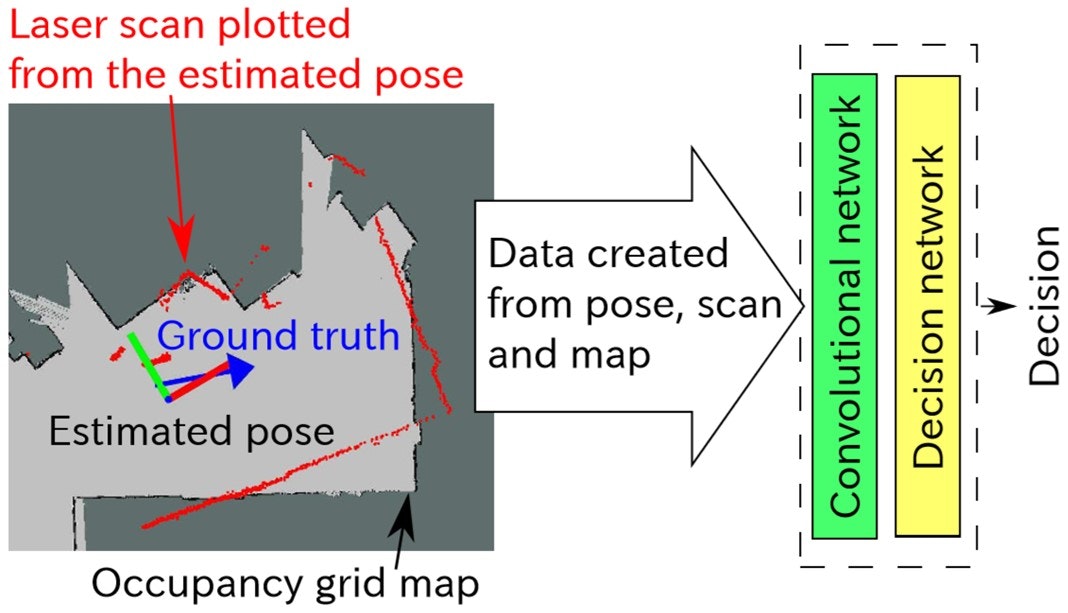
自己位置推定は,「センサ観測と地図照合する」ことで行われます.すなわち「自己位置推定の失敗」とは,「センサ観測と地図がミスマッチしている状態」となります.例えば下図左では,黒が占有格子地図に記録されている障害物,赤がレーザスキャン(センサ観測)となっています.これらがずれているため,人目で見ればすぐに,自己位置推定に失敗してと判断できます.そこで本研究ではまず,この様なデータを深層学習(畳込みニューられるネットワーク: CNN)に入力し,自己位置推定の正誤判断を行います.
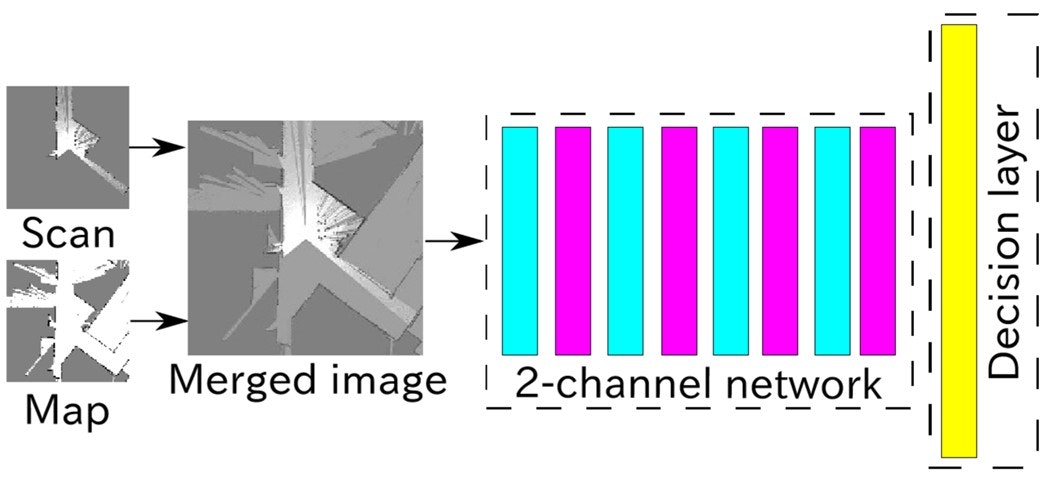
下図は,本研究で構築したCNNの概略です.まずスキャンのデータ,および推定値を中心とした地図データから,2枚のグレースケールの画像を生成します.そしてそれを重ね合わせ,CNNに入力します.この時,推定が成功している場合は1,そうでない場合は0のラベルを与え,CNNは0から1の値を回帰するように学習を行います.なお本研究で構築したCNNは,「2チャンネルモデル」というものを参考にしています(Zagoruyko ICCV2015).
本研究では,「真値と推定値の位置誤差が50㎝,もしくは3度を超えた場合」を位置推定失敗状態としています.また今回はシミュレーションを用いてデータ作成を行ったため,データに対するラベルは自動的に割り当てることができます.
CNN自体に対する検証結果の詳細は省きますが,**単純に構築したネットワークとデータセットを用いても,CNNは90%程度の精度で自己位置推定の正誤を判断できます.**画像分類などの問題と比較すると,この精度は高いといえますが,これは今回扱っている問題が比較的分類が簡単な問題であるからといえます.しかし重要なことは,**識別の精度は高いが100%にはなっていません.**すなわち,このCNNによる予測の結果をそのまま使えば,おおよそ10%は推定の正誤判断に間違えることになります.よって本研究では,CNNによる予測結果をそのまま信頼度としては使用せずに,違う方法を採用します.
位置と信頼度の同時推定問題としての定式化
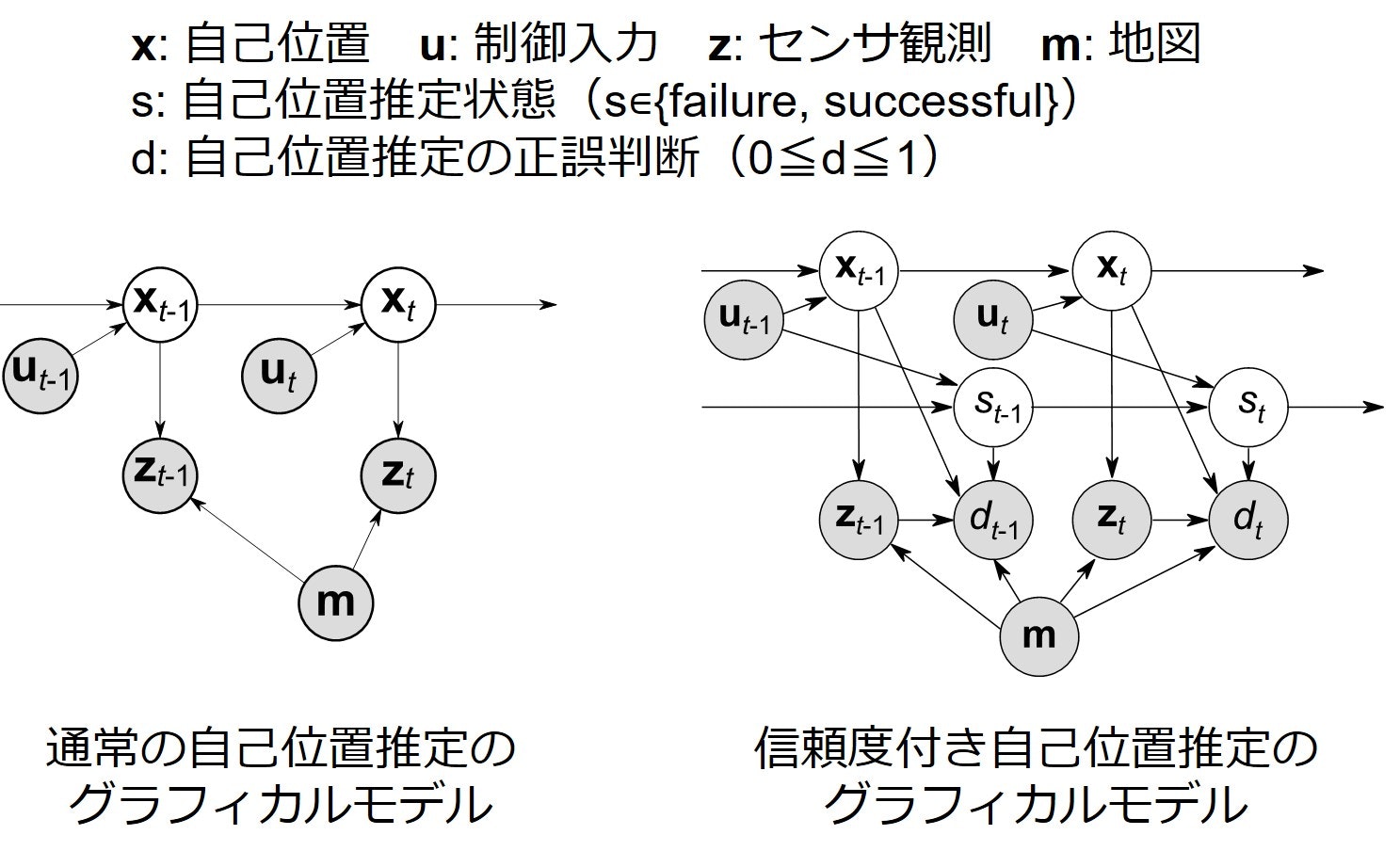
下図には,通常の自己位置推定のためのグラフィカルモデルと(左),本研究で提案している「信頼度付き自己位置推定」のためのグラフィカルモデルを示します.通常の自己位置推定のモデルは,位置${\bf x}$のみを隠れ変数(白色のノード)として扱います.一方で提案モデルでは,自己位置推定状態$s$も隠れ変数として扱います.この位置推定状態$s$は成功(successful)と失敗(failure)の2値を取ります.すなわち,$p(s={\rm successful})$が,推定に成功している確率を表すこととなり,これが推定結果の信頼度を表すことになります.そして,CNNによる自己位置推定の正誤判断$d$が可観測変数(灰色のノード)として扱われ,これが位置推定状態に依存しいてると仮定しています.これは,CNNによる出力をある種のセンサ観測の様な値として用いて信頼度を推定するというモデルとなっています.
比較のために,両者の事後分布を計算するための式を示します.通常の自己位置推定のモデルでは,時刻$t$の位置だけを求めることが問題となり,その事後分布は以下の様になります.
\begin{split}
p({\bf x}_{t}|{\bf u}_{1:t},{\bf z}_{1:t},{\bf m})=\eta p({\bf z}_{t}|{\bf x}_{t},{\bf m})\int p({\bf x}_{t}|{\bf x}_{t-1},{\bf u}_{t})p({\bf x}_{t-1}|{\bf u}_{1:t-1},{\bf z}_{1:t-1},{\bf m})d{\bf x}_{t-1}
\end{split}
ここで$\eta$は正規化係数,$p({\bf z}{t}|{\bf x}{t},{\bf m})$は観測モデル,$p({\bf x}{t}|{\bf x}{t-1},{\bf u}_{t})$が動作モデルとなります.
一方で提案モデルの事後分布は以下の様に展開されます.
\begin{split}
&p({\bf x}_{t},s_{t}|{\bf u}_{1:t},{\bf z}_{1:t},d_{1:t},{\bf m})\\
&=\eta p({\bf z}_{t}|{\bf x}_{t},{\bf m})\sum_{s_{t}}p(d_{t}|{\bf x}_{t},s_{t},{\bf u}_{t},{\bf m})p(s_{t}) \int p({\bf x}_{t}|{\bf x}_{t-1},{\bf u}_{t})p({\bf x}_{t-1}|{\bf u}_{1:t-1},{\bf z}_{1:t-1},d_{1:t-1}{\bf m})d{\bf x}_{t-1}\\
&\times p(d_{t}|{\bf x}_{t},s_{t},{\bf u}_{t},{\bf m})\int p(s_{t}|s_{t-1},{\bf u}_{t})p(s_{t}|{\bf u}_{1:t-1},{\bf z}_{1:t-1},d_{1:t-1},{\bf m})ds_{t-1}
\end{split}
1行目は推定する目的の事後分布です.通常の自己位置推定モデルと比較して,位置${\bf x}$と推定状態$s$の同時確率を求めていること,また,CNNによる自己位置推定正誤判断$d$が可観測変数として用いられているところが異なります.詳細は省きますが,この同時分布は乗法定理を用いることで,「位置に関する分布」と「推定状態に関する分布」に分解できます.
2行目は,「位置に関する分布」になります.通常の自己位置推定モデルもこの分布を求めていますが,**信頼度付き自己位置推定モデルでは,自己位置推定のために利用される尤度分布が2種類になります.**1つ目は,観測モデル$p({\bf z}|{\bf x},{\bf m})$で,2つ目は判断モデル$p(d|{\bf x},s,{\bf z},{\bf m})$になります.判断モデルは,CNNの出力が得られる尤度分布になります.これは,事前にCNNの判断の振る舞いをヒストグラムの様なものでモデル化することで構築できます.すなわち,CNNの出力が不安手になるということを事前にモデルに組み込むことができ,これによりCNNによる不安定な出力に対する影響を軽減できるようになります.
3行目は推定状態に関する分布になります.この部分に関する説明は割愛します.
論文中では,上式の確率分布をRao-Blackwellized Particle Filter (RBPF)を用いて解きます.これはFastSLAMなどでも使われているテクニックであり,これを簡単に言うと,「2つの分布を求める際に,1つの分布をサンプリングベース(例えばパーティクルフィルタ)の手法で求め,もう1つの分布をサンプルされた状態を基に解析的に求める」という方法です.信頼度付き自己位置推定では,位置に関する分布をパーティクルフィルタで求め,推定状態に関する分布を解析的に求めます.
信頼度付き位置推定の結果
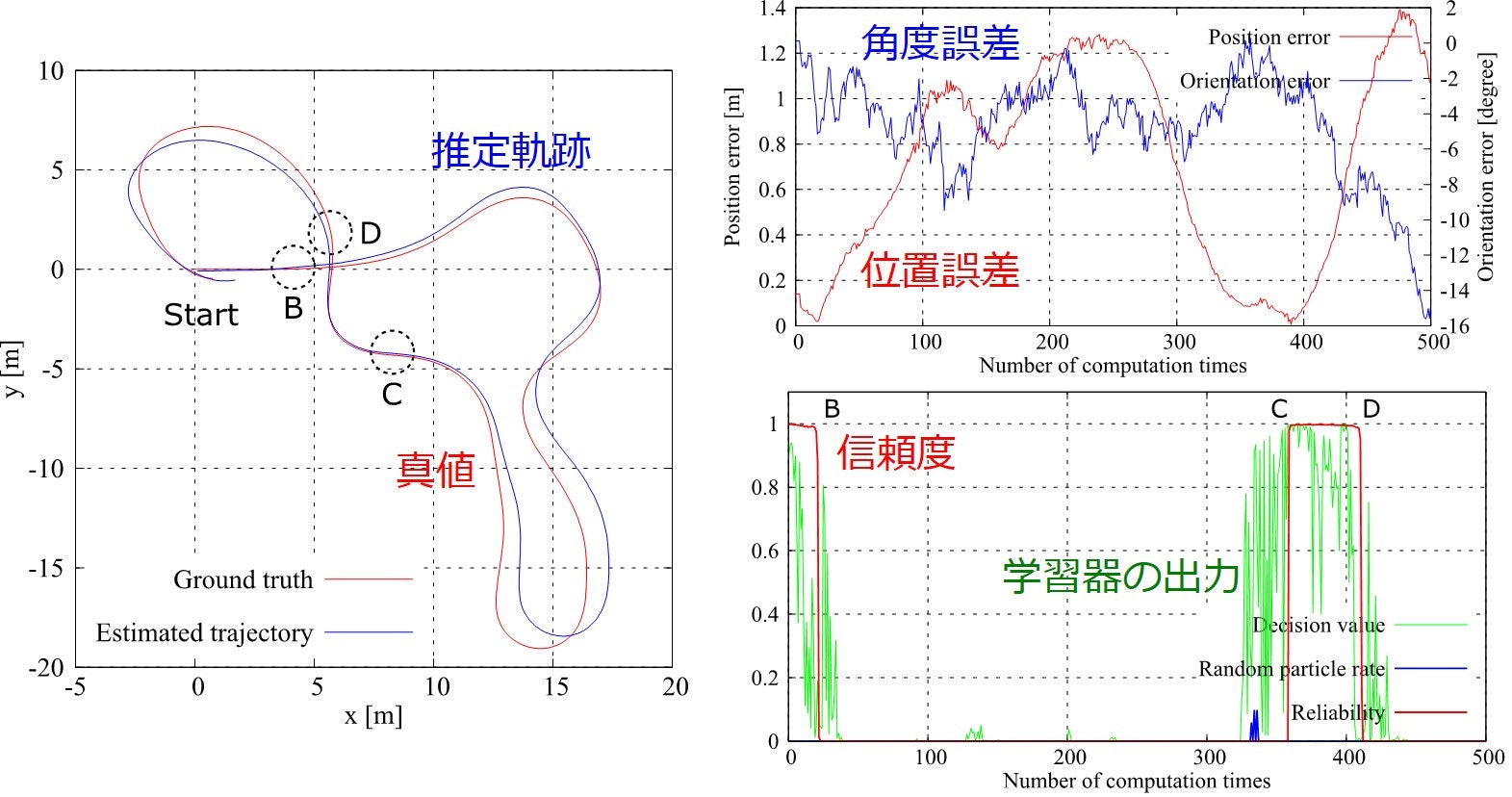
わざと位置推定に失敗する条件で実験した際の結果が下図になります.
左図は真値(赤)と推定軌跡(青)を示しています.右上図が位置(赤)と角度(青)の誤差になります.右下図が,推定された信頼度(赤)と,最尤パーティクルに対するCNNの出力(緑),比較手法として利用したAugmented MCL (AMCL)により推定された失敗かどうかの判断値(Random Particle Rate)(青)になります.なおAMCLの値は,0を超えた場合に失敗を検知したことになります.
位置誤差の増大に合わせて,信頼度が適切に増減していることが確認できます.一方で,CNNの出力が不安定に振動していることも確認できます.なおComputation timeの間隔は0.1秒となっています.この結果から,推定された信頼度が,CNNよりも安定して位置推定の正誤を説明できていることが確認できます.
以下に,シミュレーション実験に関する動画もアップしています.障害物が多数存在する動的な環境でも,安定して信頼度が推定できていることが確認できます.
Reliability estimation for mobile robot localization in highly dynamic environments
まとめ
私の論文を紹介しました.自己位置推定結果に対する信頼度を求めるための「信頼度付き自己位置推定モデル」に関するものです.
通常の自己位置推定を行ったとしても,推定結果に対する確信度しか得られず,これは信頼度とは異なります.信頼度付き自己位置推定モデルでは,自己位置${\bf x}$と同時に自己位置推定状態$s$を求め,この推定状態に関する確率を求めることで信頼度を推定します.また論文では,この推定状態を求めるためにCNNを活用しました(実際にはCNN以外の実装方法も考えられますが,今回は精度の点からCNNを採用しました).
結果として,CNNを用いて暗に自己位置推定の正誤を判断するより,信頼度を用いて安定して自己位置推定正誤を説明できることを示しました.