紹介する論文
論文の要約
- Localize(自己位置推定)とAbility(能力)を合わせた造語である「Localizeability」を点群地図上で予測する方法を提案している
- マッチングした点群の法線ベクトルを並べた行列に主成分分析を適用し,その最小の固有値をLocalizeabilityを表す値として利用する
- Localizeabilityが低い地点で,自己位置推定の誤差が増大することが確認されている
はじめに
「Localizeability」とはLocalize(自己位置推定)とAbility(能力)を合わせた造語です.すなわち「自己位置推定が成功する可能性」というような意味になります.本論文では,3D LiDAR(回転式2D LiDAR)を搭載したドローンが3次元点群地図を用いて自己位置推定を行う場合のLocalizabilityを予測・計算する方法を提案しています.
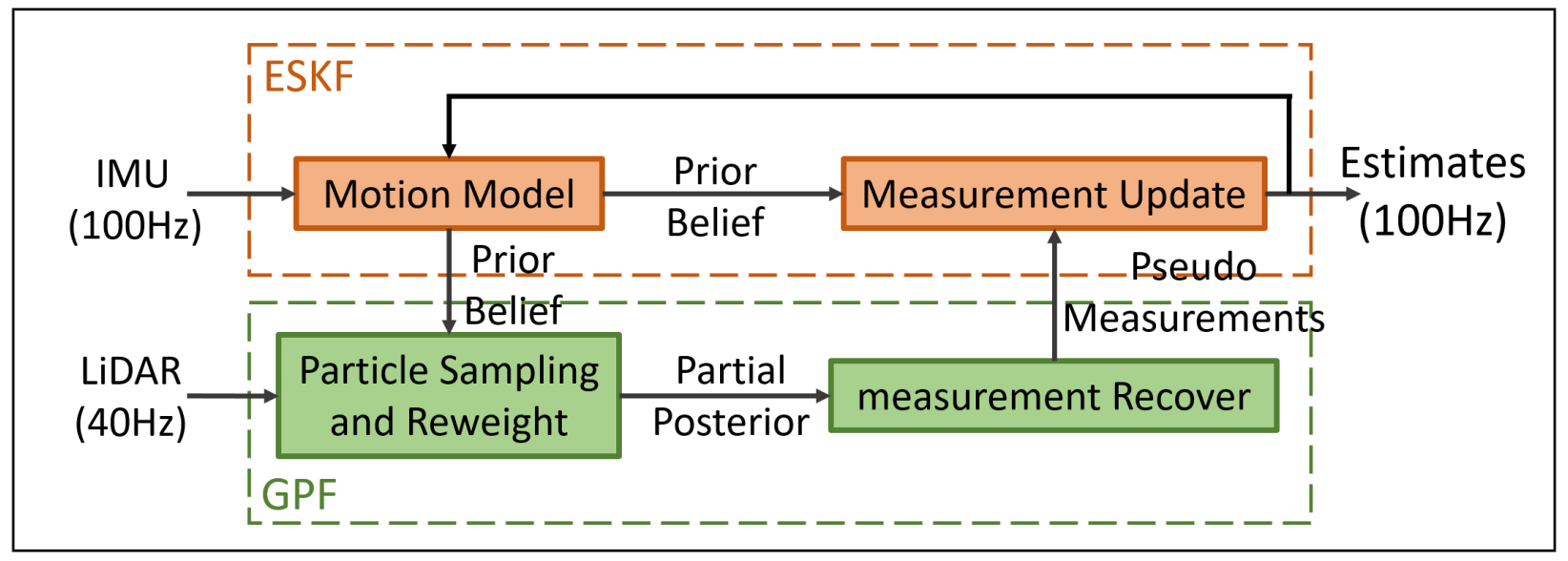
また自己位置推定法も少し変わったものを提案しており,Error State Kalman Filter(ESKF)とGaussian Particle Filter(GPF)を用いています.GPFを用いて擬似観測(pseudo measurements)を作りだし,それをESKFで統合して自己位置推定を行うという方法となっています.
自己位置推定手法
上図(論文中図2)に自己位置推定に関するブロック図が示されています.ESKF内において,IMUを用いて位置の予測が行われます(この処理はほぼ通常のKalman filter(KF)と同じといえます).この予測した誤差分散がGPFに渡され,この分布を基に,まずパーティクルのサンプリングが行われます.次に,パーティクルの尤度計算を尤度場モデル(確率ロボティクスを参考にして下さい)に従って行い,その尤度を用いた重み付き平均と分散を計算します.この平均と分散を基に,擬似観測を生成します(論文中の式(7)と(8)).この擬似観測の生成は,KFにおける観測による更新を逆にすることで達成できます.最終的に,この擬似観測がESKFに与えられることで,観測モデルによる更新が行われ,最終的な自己位置推定が結果が出力されます.
なお,一般によく使われるextended Kalman filuter(EKF)とESKFの違いは論文中の引用文献[11]で議論されているようです.
Localizabilityの計算
まず前提として,ある観測点$p_{i}$が地図にある平面とマッチングしているとき,その平面に属する点$p_{i,0}$と$p_{i}$により構成されるベクトルは,その面の法線ベクトル$n_{i}$と直行するので,その内積は0となります(論文中式(13)).
$$
n_{i}^{T}(p_{i}-p_{i,0})=0
$$
またセンサの観測値$r_{i}$は,ロボット位置$x$から点$p_{i}$までのオフセット量として考えることができ,$x+r_{i}=p_{i}$という関係が成り立ちます.なお,$x$は3次元空間場での位置のみを表し,姿勢の情報を含みません.この関係を上式に代入すると,次式(論文中式(14))を得ることができます.
$$
n_{i}^{T}(x+r_{i}-p_{i,0})=0 \rightarrow
n_{i}^{T}x=n_{i}^{T}(p_{i,0}-r_{i})=d_{i}
$$
ここで$d_{i}$は定数ベクトルとなります.そして,すべての観測を集約した行列を作成することで,次式(論文中式(15))を得ることができます.
\left[
\begin{matrix}
n_{1_{x}} & n_{1_{y}} & n_{1_{z}} \\
n_{2_{x}} & n_{2_{y}} & n_{2_{z}} \\
\vdots & \vdots & \vdots \\
n_{k_{x}} & n_{k_{y}} & n_{k_{z}}
\end{matrix}
\right]
=\left[
\begin{matrix}
d_{1} \\
d_{2} \\
\vdots \\
d_{k}
\end{matrix}
\right]
\rightarrow
Nx=D
上述した$N$は,観測によって得られた自己位置推定実行のための拘束を表した行列とも解釈できます.この$N$に対してPrincipal Component Analysis(PCA)を実行すると,平面の法線ベクトルに基づく制約により得られた正規直行基底が得られます(ここ良く意味がわからないですね...).なお論文では,
The matrix $N$ describes the set of observable constraints from the given pose. Preforming a principal component analysis (PCA) on the row vectors of $N$, provides an orthonormal basis spanning the space described by the constraints from the surface normals.
と述べられています.
さらに$N$に対して,特異値分解(Singular Value Decomposition)を適用し,$N=U\Sigma V^{T}$を得ます.ここで$\Sigma$は,制約の累積強度を表します(これも難しいですね...).本論文中では,この$\Sigma$の対角成分の最小値が,Localizabilityを表す値として用いられています.
このLocalizabilityの性能の一例として,下図(論文中図3)に例が示されています.左図が最大計測距離5m,右図が最大計測距離10mの例をそれぞれ示しており,青がLocalizability低い地点,赤がLocalizabilityが高い地点を示しています.前後左右の制約となるランドマークが観測できる地点では,確かにLocalizabilityが低くなっていることが確認できます.
また実験の章において,下図(論文中図11)が示されており,確かにLocalizabilityが低い地点で位置推定誤差が大きくなることが示されています.
個人的解釈
行列$N$に対するPCAの結果は,地図と観測により構成される法線ベクトルのバラつきのようなものと解釈できると思います.すなわちもしPCAの結果,第1主成分の累積寄与率が95%とかなってしまうと,95%の観測が1方向の拘束しか与えていないと解釈できるのだと思います.なので,理想的にはすべての成分の寄与率が30%程度となると,どの方向も拘束できるようになるのだと考えられるのだと思います.しかしこれだと,位置成分しか拘束できず,角度成分を拘束できないような気もします...
また,本論文で議論されている方法には,環境の動的変化に対する脆弱性があるのかと思います.そもそも,得られている制約が正しい制約,すなわち地図と観測の対応が正しいのか,という前提は考慮していないため,環境変化によるこれらの影響はかなり受けてしまうものと思います.
感想
Localizabilityという発想は面白いですね.しかし,Localizabilityの計算が環境の動的成分を考慮できるような方法論になっていないと考えられるので,このあたりは引き続き研究が必要だと思えました.そのためにも,結局地図と観測の対応が正しいのかという本質を扱わなければいけないなと強く感じます.