巡回セールスマン問題をPythonで考える

はじめに

あなたは巡回セールスマン問題、という最適化問題を知っていますか？

巡回セールスマン問題とは、複数の決められた地点をセールスマンが巡回して元に戻る際、どう回れば最も移動距離が少なく、効率が良いのか、を考える問題です。最近では、物流の2024年問題の解決の鍵にもなると言われ、注目されていますよね！

まあそんなこんなで、巡回セールスマン問題は、物事をどのように行うのが最も効率が良いのか考える、とっても身近なお話なわけです。使いこなせたら便利ですよね☆*:.｡. o(≧▽≦)o .｡.:*☆

ということで、今回は簡単に複数の目的地を効率よく回る方法を考えたいと思います、Pythonで。

参考：
物流の2024年問題
https://www.ntt.com/bizon/d/00492.html
巡回セールスマン問題(traveling salesman problem、TSP)
https://www.msi.co.jp/solution/nuopt/docs/examples/html/02-12-00.html

1. 前提

今回はPuLP（Pythonで数理最適化問題を解くためのライブラリ）を用いて5地点の最適な周り方を考えたいと思います。

参考：
最適化におけるPython（PuLP版）
https://qiita.com/SaitoTsutomu/items/070ca9cb37c6b2b492f0

2. コードを書く

以下、実行したコードを示しますが、何をしているのか簡単に説明すると、
・目的関数は総移動距離の最小化
・制約条件は各都市からの出発・到着が1回
・サブツアー（部分的に閉じたルート）除去の制約
これらを線形計画問題として定式化し、CBCソルバー（Coin-or Branch and Cut solver）で解きました。

import pulp
import math

# ５地点
points = [
    ("P1", 35.6804, 139.7690), 
    ("P2", 35.6916, 139.7003),  
    ("P3", 35.6586, 139.7454), 
    ("P4", 35.6897, 139.6921),
    ("P5", 35.6894, 139.6917), 
]

n = len(points)

# 距離をユークリッド距離で定義
def euclidean_distance(p1, p2):
    return math.sqrt((p1[1] - p2[1])**2 + (p1[2] - p2[2])**2)

# 距離を辞書形式で保持
dist = {}
for i in range(n):
    for j in range(n):
        if i != j:
            dist[(i, j)] = euclidean_distance(points[i], points[j])
x = pulp.LpVariable.dicts('x', (range(n), range(n)), cat=pulp.LpBinary)

problem = pulp.LpProblem('TSP', pulp.LpMinimize)

# 目的関数: 移動距離の合計最小化
problem += pulp.lpSum(dist[(i, j)] * x[i][j] 
                      for i in range(n) for j in range(n) if i != j)

# 各都市からの移動は一回
for i in range(n):
    problem += pulp.lpSum(x[i][j] for j in range(n) if i != j) == 1

# 各都市への移動も一回
for j in range(n):
    problem += pulp.lpSum(x[i][j] for i in range(n) if i != j) == 1

# サブツアー(部分巡回)除去用の変数 u[i]
# MTZ (Miller-Tucker-Zemlin)
u = pulp.LpVariable.dicts('u', range(n), lowBound=0, upBound=n-1, cat=pulp.LpInteger)

# i=0 を出発都市と仮定してサブツアー除去
# i!=0, j!=0 の i->j 移動に対して: u[i] - u[j] + n*x[i][j] <= n-1
for i in range(1, n):
    for j in range(1, n):
        if i != j:
            problem += u[i] - u[j] + n * x[i][j] <= n - 1

# CBCソルバーを使用
problem.solve(pulp.PULP_CBC_CMD(msg=0))  

print("Status:", pulp.LpStatus[problem.status])
print("Objective value (Total Distance) =", pulp.value(problem.objective))

# 解の取り出し
route = []
current_city = 0
route.append(current_city)
visited = set([current_city])

for _ in range(n-1):
    for j in range(n):
        if j not in visited and pulp.value(x[current_city][j]) == 1:
            route.append(j)
            visited.add(j)
            current_city = j
            break

# 最後に出発点に戻る
for j in range(n):
    if pulp.value(x[current_city][j]) == 1 and j == 0:
        route.append(0)
        break

print("Route (city indices):", route)
print("Route (city names):", [points[i][0] for i in route])

この結果を図示するために次のコードを実行します。

import folium
from folium.plugins import PolyLineTextPath

# route の順に (緯度, 経度) を並べ替えた配列
route_coords = [(points[i][1], points[i][2]) for i in route]
# 中心点 (平均座標)
center_lat = sum([p[1] for p in points]) / len(points)
center_lon = sum([p[2] for p in points]) / len(points)

# Foliumマップを生成
m = folium.Map(location=[center_lat, center_lon], zoom_start=13)

# 各都市をマーカーで表示
for i, (city, lat, lon) in enumerate(points):
    folium.Marker(
        location=[lat, lon],
        popup=f"{city} (index={i})",
        icon=folium.Icon(color="red", icon="info-sign")
    ).add_to(m)

# 青線
line = folium.PolyLine(
    locations=route_coords,
    color='blue',
    weight=4,
    opacity=0.7
).add_to(m)

# 矢印の描画
PolyLineTextPath(
    line,
    '  ➡  ',  
    repeat=True,
    offset=7, 
    attributes={
        'fill': 'blue', 
        'font-weight': 'bold',
        'font-size': '16'
    }
).add_to(m)

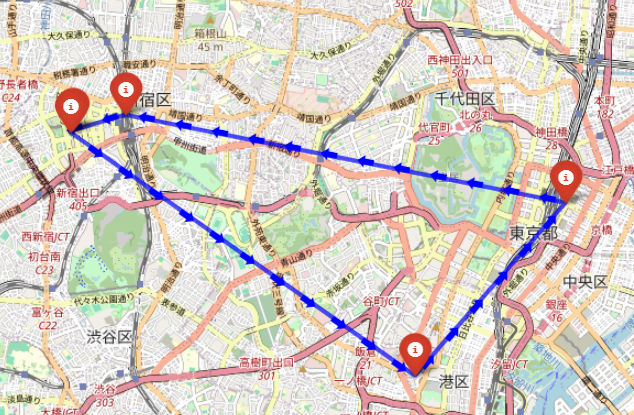
表示された地図は以下のようでした。

ちょっと地点の取り方が簡単すぎたかなとも思いますが。。。
今回はこのくらいで許してください。。。

おわりに

次のラボ旅行では、巡回セールスマン問題を使って最も効率よく観光したいですね！( ^^) _U~~