あなたは、最適輸送を知っていますか?
最適輸送とは、ある確率分布に従う質量(あるいは確率)を、別の確率分布に移動させるために必要なコストを最小化する輸送方法を求めることです。まあ最適輸送についての説明記事は世の中に五万とあるので、気になった方は調べてみてください。
ところで、最適輸送といえば、私の中で伝説の記事があります。
この記事では、披露宴の席決めを最適輸送を用いて行っています。
ちょうど、弊研究室は来年の春に居室のお引越しがあるので、上記の記事をオマージュして、我々も新しい席配置を最適輸送で決めたい、そんな気持ちでこの記事を書いてみます。
前提
学生16人と大人4人の最適配置を行う。
今回は適当に、以下のような配置にすることにした。また、小文字が学生の席、大文字が大人の席を想定している。
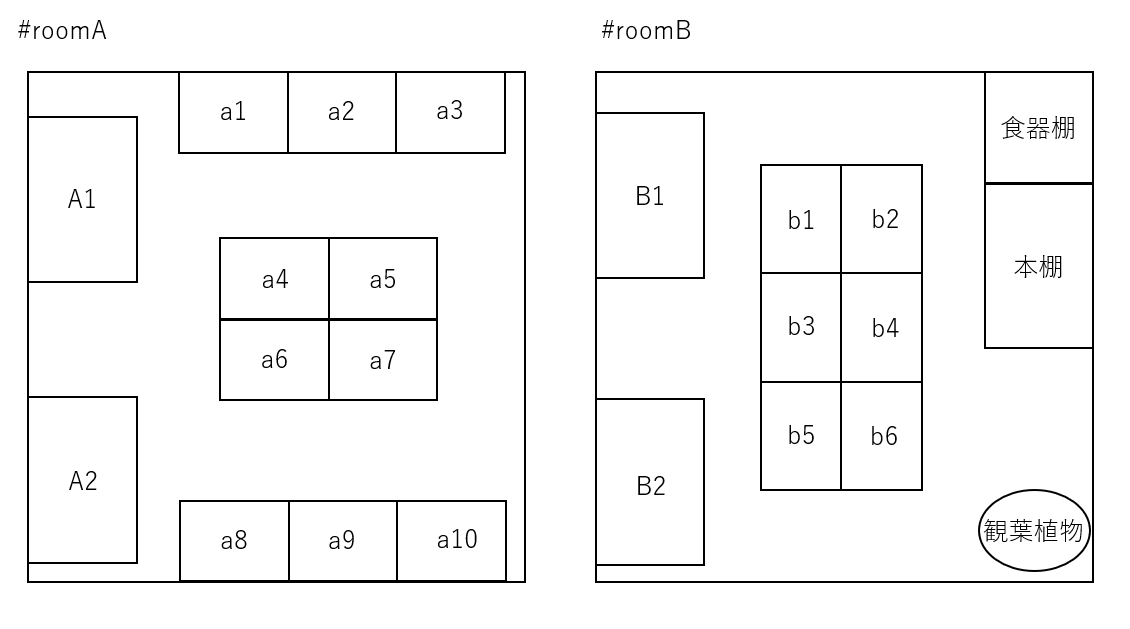
定義
まず、登場人物は次のように定義する。
学生:U1, U2, U3, U4, U5, M1, M2, M3, M4, M5, M6, M7, M8, D1, D2, D3
大人:O1, O2, O3, O4
座席の関係性については以下のように定義した。この状態をSとする。
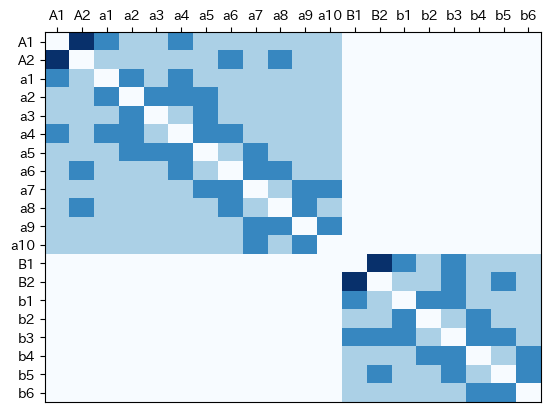
次に、個人間の関係性の定義のため、ひとまず10クラスターを定義した。
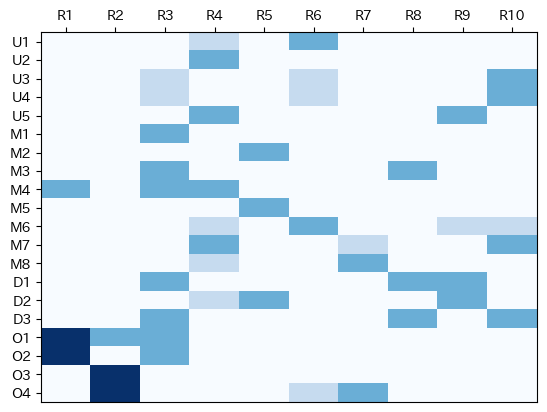
すると、個人間の距離は以下のように定まる。この状態をDとする。
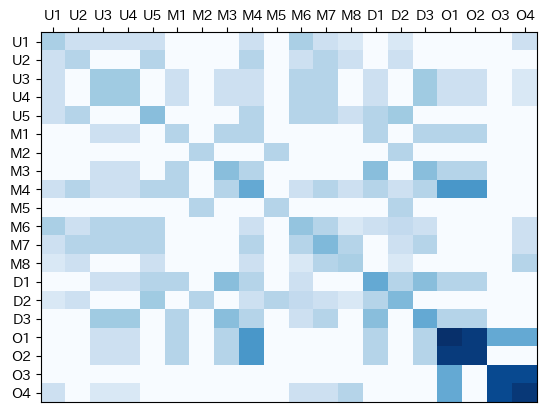
類似度行列を正規化された距離行列に変換し、対角要素を0に設定する。
#座席について
dist_S = (S.max()-S)/(S.max()-S.min())
np.fill_diagonal(dist_S, 0)
#個人間の距離について
dist_D = (D.max()-D)/(D.max()-D.min())
np.fill_diagonal(dist_D, 0)
POTよりgromov_wassersteinを用いてこの問題を解く。
今回は、大人を指定した席に座らせたかったので、その部分に重みを付けた。
G0 = np.ones([20, 20]) * 0.01
G0[17, 1] = 0.05
G0[19, 13] = 0.05
G0 /= G0.sum()
p=G0.sum(axis=1)
q=G0.sum(axis=0)
gw, log = ot.gromov.gromov_wasserstein(
dist_S, dist_D, p, q, 'square_loss', log=True, verbose=True, G0=G0)
ここまでを実行すると以下のような結果が得られた。
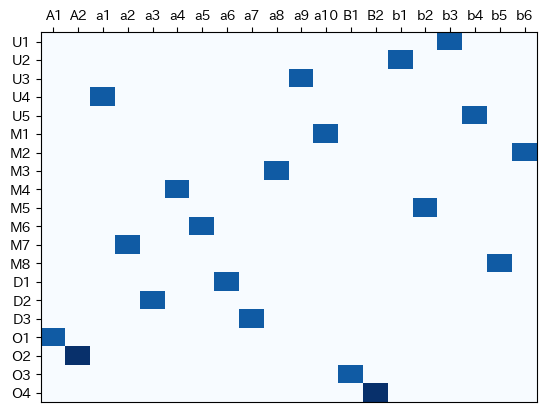
図面に起こしてみるとこんな感じらしいです。
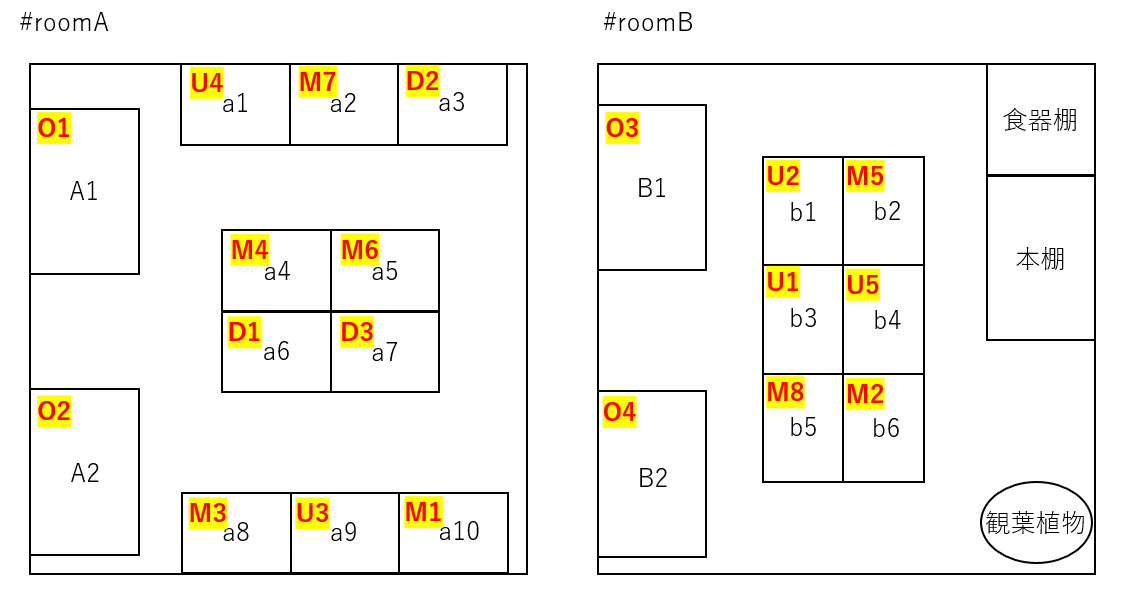
おわりに
わたし、壁際に座りたいので、この席順は却下でおねがします(^_-)-☆