Quaternion(unityの回転)について

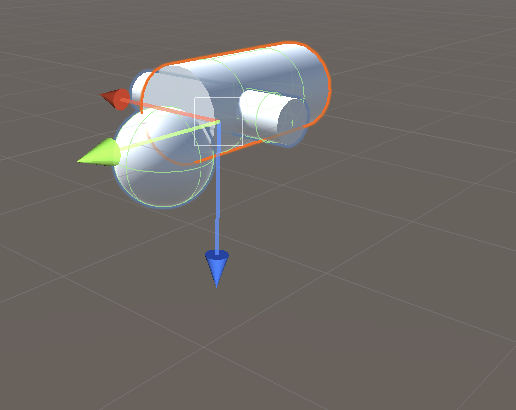
注意事項

ガバです。だいたいQuaternionクラスの使い方のような内容になっています。またUnityの回転の仕様を理解している方は読まなくて大丈夫です。

オイラー角

まず普段私たちがUnityのInspector上で見ている角度は私たちが直感的にわかるようにオイラー角という表現で作られています。これは自身の〜軸を中心にどれだけ回すということを軸分やるという手法で回転する考え方であり（本筋の考え方は違うが今回はこれで考える詳しくは他のサイトで）Unityではz→x→y軸の順番で回すようになっています。
なんでこんなことを書くかというとこの軸の順番によって回された結果というのは大きく変わって来るからです。言葉で見てもわからないので実際にエディター上で見て見ましょう。

using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class GimbalLock : MonoBehaviour
{
    [ContextMenu ("Experiment")]
    public void Experiment1()
    {
        transform.Rotate(new Vector3(90, 90, 0),Space.World);
    }

    [ContextMenu ("Experiment2")]
    public void Experiment2()
    {
        transform.localRotation *= Quaternion.Euler(90, -90, 0);
    }
}
 

[ContexrMenu("nantoka")]でコンポーネント上で右クリックするとその関数のみ実行できる様になります。

上のコードを実行する前に一度Experiment1,2の動きを考えてみてください。

Experiment1はワールド座標基準でオブジェクトを回転させています。なのでお辞儀した形でy軸方向に回るでしょう。

Experiment2はどうでしょうか。こちらはローカル座標中心に回転させていますのでお辞儀するまでは同じでも、その後は自分のy座標に従い横を見る様な形に回転するはずです。

しかし実際は

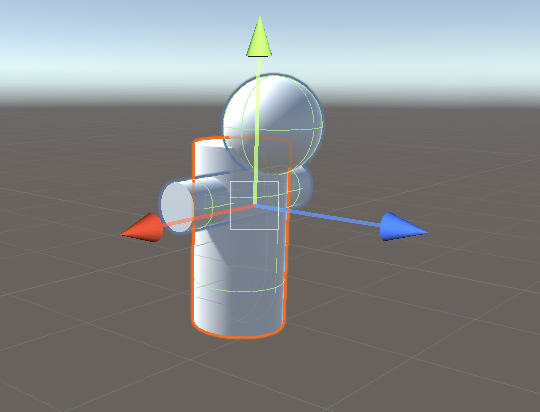
結果の画像を見ると明らかにz軸中心に回転しています。これはExperiment1,2どちらもこの結果になってしまうのです。Experiment2はおかしな結果なはずです。

しかしこの現象にはきちんと理由があります。それはジンバルロックという現象です。

Gimbal lock(ジンバルロック)

オイラー角の説明で三軸を〜度回すことで回転を実現させる考え方だと説明しました。これとジンバルという機器は同じ手法を用いています。そしてこの手法に付いて回って来るのがジンバルロックという現象です。
Unityのシーン上でオブジェクトを選択し，三軸を表示させてください。この回転させる軸が三つある状態を自由度が３と言ってようするに三つのパラメーターで今オブジェクトが操作できている状態ということになります。この時ジンバルロックが起こります。
ではジンバルロックというのはどのような現象かというとある回転軸が他の軸の方向に重なってしまった時に自由度が２になり，二つの成分しかいじれなくなってしまうという現象です。

試しにエディタ上でrotation.xを９０にしてからドラッグしてy，zを変えて見ましょう。すると同じ動きしかしません。これはx軸中心に９０度倒れたことで回転するy軸と通常のz軸が重なってしまったためにジンバルロックが起こってしまったせいで自由度が２になりz軸の回転のみ有効になってしまった為このような現象が起こってしまったのです

上記でいずれかの軸で９０度回転を起こした時にジンバルロックが起こるという数学的な証明がされています。興味のある方は読んでください。

ジンバルロックを視覚的に表した動画

Unity公式のリファレンスではいずれかの回転軸が第一，第二の回転により第三の回転軸に重なってしまったがために第三の回転軸特有の回転（独立した回転）にならなくなってしまうと書いてあります。これの方がわかりやすいかもしれません。

三軸で回転を表そうとするとこのような問題が出てしまいます。なので４つ目の要素を使った四元数（Quaternion）を使うわけです。

Quaternionとは

簡潔にいうと四次元のベクトルです。高校までの間で複素数平面を習ったと思いますが，これを回転に置き換えてみると平面上での回転を二要素x，yで表していたということになります。では三次元ではどうか複素数平面から複素数空間に拡張されたわけです。そこで出てきたのが四元数です。

上記サイトに細かいことは書かれていますが，正直いろいろなサイトを見た結果ほとんど理解できませんでした。わかったことを書いて行くと

• Quaternionのq１とq２は互いにベクトルでありながらも積をすることが可能。
• またQuaternionの第四成分を０にし積を出すと３次元ベクトルの外積を出したことと同じになる。
• q１で回転させそのあとq２で回転させた結果はq２q１と同じになる

ということでした。三つ目のおかげでUnityでは容易にQuaternionを用いた回転ができるそうです。よかったですね。

Quaternionの使い方

Quaternionの計算は乗算で行われます。感覚で（０，０，０）をy軸中心に回したいからといって＝（０，３０，０）としてはいけません。これはQuaternionがスカラー量ではなくベクトルであることから二次元ベクトルの回転の計算を思い出せばわかっていただけると思います。
Quaternion同士の計算をしなくてはいけない理由はUnityのTransform.rotationはQuaternion型だからということで解決します。

また後述のコードの中にはジンバルロックが起こる可能性があるものがいくつかあります。通常ジンバルロックが起こるということはないと思うのでそこまで気にする必要はないです。

以下のコードは

a*=b*c

という手法をとっていますがこれは正確ではない場合があります。なぜかというとこの計算方法でいくとc回転->b回転という処理になってしまうからです。前から順番に回転させたい場合はちゃんと

a=　a*b*c

と書きましょう。

Quaternion基本操作

Quaternion.AngleAxis(hogehoge,Vector.hoge)
これはhogehoge度Vector.hogeを中心に回転させたい場合に使います。

 void QuaternionAngleAxis()
    {
        transform.rotation*=Quaternion.AngleAxis(30, Vector3.up);
    }

Quaternion.Euler(x,y,z)
あれ？オイラー出てきたじゃんQuaternionじゃないよ！嘘つき！と思った方もいるかもしれませんがこれはQuaternionの回転をオイラー角表現にしているだけでQuaternionです。ただ上でやった例の通りジンバルロックが起こる可能性があります。

    void QuaternionEuler()
    {
        transform.localRotation *= Quaternion.Euler(0, 30, 0);
    }

Transform.LookAt(Target.transform,Vector3.up)
引数１に向かせたいオブジェクト，２に上方向のベクトルを設定します。通常２つ目は書く必要はありません。これは通常何かに対してずっと注視しててほしいカメラなどのオブジェクトにつけられますが，後述するコードによって追いかける緩急をつけられる高度なメソッドがあるので見て欲しいオブジェクトが決まっているときにのみ使えば良いと思います。

Transform.Rotate(x,y,z,Space.World)
Quaternionの項目ですが，オイラー角を用いたものです。これは自身のトランスフォームに角度を加算して方向を変えます。正直これは使わなくてもいけそうな気がしますが，現在の角度から何度回転というのが決まっているときはこれでも良いのかなと思ったり。ただしジンバルロックが起こるので注意。

    void TransformRotate()
    {
        transform.Rotate(0, 30, 0,Space.World);
    }

四つめの引数にはワールド座標で回転させるかローカル座標で回転させるかを指定できます。親子関係を持つオブジェクトの子のみを回転させたい場合はワールド座標を指定したほうが良いでしょう。

Quaternion応用編

Quaternion.Slerp(transform.rotation,targetRotation,speed（＜＝１）)
これを使うとある方向，角度へある一定のスピードで回転させることが可能になります。実際に挙動を見た方が良いと思います。

    public float t=0.1f;
    public void Update()
    {
        Quaternion from_qua = Quaternion.Euler(0f, 0f, 0f);
        Quaternion to_qua = Quaternion.Euler(0f, 0f, 180f);
        this.transform.rotation = Quaternion.Slerp(from_qua, to_qua, t);
    }

これを例えばPlayerにアタッチすると１８０度回転を10秒の間でやってくれます。speedは０から１までの範囲で入れることができ，初期値を設定し直すことで好きな速度で回転させることができます。ではカメラにこのメソッドを使ってPlayerを追いかけるスクリプトにするにはどうすれば良いでしょうか。

    public float t=0.1f;
    public GameObject target;
    public void Update()
    {
        Vector3 targetPos = target.transform.position - transform.position;
        Quaternion targetRotation = Quaternion.LookRotation(targetPos);
        transform.rotation=Quaternion.Slerp(transform.rotation, targetRotation, t);
    }

今回はこれをPlayerにアタッチしてターゲットをCubeにしました。するとCubeを見続けるPlayerを作ることができます。これをカメラに適用してターゲットをPlayerにすれば良いということです。
このコードの解説をするとまずターゲットに対しての自身からのベクトルを五行目で作りLookRotationというメソッドを用いてベクトルをその方向への回転へと変換しています。あとはSlerpに入れるだけです。

その他のQuaternion

他にもUnityのリファレンスに書いてあるQuaternionメソッドについて解説します。
Quaternion.Inverse（Quaternion hoge）
hoge方向への回転の逆回転を返します。つまりhogeとかければ無回転状態になります。

Quaternion.identity
無回転を取得します。Instantiateを使うときによく引数として用いられます。

Quaternion.FromToRotation(Vector3.hoge,transform.hoge)
transform.hogeを中心にしてVector3.hogeの方向へ向きます。ジンバルロックに注意してください。

Quaternion.RotateTowards(transform.rotation, targetRotation, step)
Quaternion.Slerpに似た動きをします。違うのが三つ目の引数は回る速さではなく，回る大きさの変化に関わってくることです。速さと変わりがないようにも思えますが，微妙な挙動の違いがあります。

public GameObject target;
    public float step;
    public void Update()
    { 
        Vector3 targetPos = target.transform.position - transform.position;
        Quaternion targetRotation = Quaternion.LookRotation(targetPos);
        transform.rotation = Quaternion.RotateTowards(transform.rotation, targetRotation, step);
    }

Quaternion.LookRotation（target.transform.position,Vector3.up）
オブジェクトの正面がz軸方向，頭上がy軸方向の時に働くスクリプトです。Slerpの時に解説しましたがこれ単体でも使えます。これは例えば正面を向いたまま上に何度か動かしたい時，つまり見せたい時にその対象へのベクトルを引数１に入れることで動作します。

終わり

今回の記事でQuaternionに詳しくなれれば幸いです。かなり専門的な分野も関わる話ですのでガバがあれば修正リクを出してくださるとありがたいです。

修正

今回の記事自体はだいぶ前に大学内のサークル用に書いたものだったのでどういう記事を参考にしていたのかが曖昧だったんですが、ソースコードを見るに恐らくこちらの記事の内容も参考にしていたので貼っておきます。