さいしょに
この記事ではRで実験計画法の応答曲面法で最適化を行う方法について紹介します。
実験計画法とは?
詳細はリンク先に任せますが、実験計画とは特に製造業や薬などの開発において、どのように実験を設計すると良いか、という考え方であり実践方法です。例えば、原材料の量・反応温度などが説明変数、収率が目的変数とする場合を想定します。このとき、総当たりでやるにはコストがかかりすぎるが、適当に行き当たりばったりでやっては見落としが発生してしまう、というので良い感じの組み合わせを考える必要があり、統計的に無駄なくやっていこうという思想です。
実験計画法とは、少ない実験(シミュレーション)回数から精度の良い結果の情報を、効率良く取り出すための実験配置が計画された手法です。
応答曲面法とは
応答曲面法というのは、その実験計画法の中のひとつです。簡単に言ってしまえば、応答値(目的変数:Y)を曲面、つまり二次関数でモデルを立てましょう、という手法です。それを等高線などで表現し、こういう条件であれば目的変数が規格を満たすことが出来そうだ、とかこの条件で最大値(最小値の場合もアリ)を取りそうだ、とかそんな感じで用います。
具体的には、上と同じ例ですが収率を最大化するため工場の製造条件(反応温度や原材料の量)を見直す、みたいなときに使います。
応答曲面法は、不連続なデータを連続的な曲面として近似したモデルを作成する手法です。
本記事のモチベーション
現在(2025年4月)においても、製造業での開発は結構勘や経験に頼っている面があります。このあたり、過去のデータを全部AIに渡せるような形式になっていればAIでの代替が可能なのでしょうが、実際はそうなっておらず、各々の頭の中にだけ残っているというのが現状です。
自分の肌感覚では、開発で経験を積んで来た人は比較的高齢で、プログラミングは全くダメという人も多く見られます。そのため、ベテラン開発者の勘を活かしつつ、実験計画法を用いて開発期間を短縮していく、というのは、少なくとも向こう数年間は需要があるのではないかな、と思い記事を作成しました。
Rでやっていこう
今回はrsmを用いてやってみます。rsm::ChemReactを追体験していくような形で進めてみましょう。
さいしょにrsmを読みこみます。
library(rsm)
実験計画を立てるまで
2因子の中心複合計画を作成します。いきなり訳わからない単語ですが、ここではまあいくつかある型の中のひとつという認識でお願いします。
# 2因子 (k=2) の中心複合計画を作成
ccd_plan <- ccd(
basis = 2, #因子数
n0 = c(3, 3), #センター点を各ブロックで何回取得するか
alpha = "rotatable", #star点をどう取得するか、ここは別のサイトで参照してもらうとして、、、
randomize = FALSE, #ランダム化を行うか、実際はランダム化して実験を進めた方が良いが、今回はお試しなのでFALSEを入れる
coding = list(x1 ~ (Time - 85) / 5, x2 ~ (Temp - 175) / 5) #時間を85±5, 温度を175度±5で条件振りすると設定
)
中身を確認するとこんな感じになっています。つまり、中心複合計画(rotatable)で実験計画を立て、そのパラメーターは時間を85±5秒, 温度を175±5度で条件を振って最適化しようとした場合、下の条件表に沿って実験をしましょうね、となります。(本来はrondomize = TRUEにして出てきた表に従った方が良いです)
> ccd_plan
run.order std.order Time Temp Block
1 1 1 80.00000 170.0000 1
2 2 2 90.00000 170.0000 1
3 3 3 80.00000 180.0000 1
4 4 4 90.00000 180.0000 1
5 5 5 85.00000 175.0000 1
6 6 6 85.00000 175.0000 1
7 7 7 85.00000 175.0000 1
8 1 1 77.92893 175.0000 2
9 2 2 92.07107 175.0000 2
10 3 3 85.00000 167.9289 2
11 4 4 85.00000 182.0711 2
12 5 5 85.00000 175.0000 2
13 6 6 85.00000 175.0000 2
14 7 7 85.00000 175.0000 2
Data are stored in coded form using these coding formulas ...
x1 ~ (Time - 85)/5
x2 ~ (Temp - 175)/5
結果の入力
下のように結果を入力していきます。本来は実際に実験を行ってyieldに値を手入力する必要がありますが、今回はrsm::ChemReactの値を手入力したらどうなるか、みたいな手順で進めています。
yield <- c(80.5, 82.0, 81.5, 83.5, 83.9, 84.3, 84.0, 75.6, 78.4, 77.0, 78.5, 79.7, 79.8, 79.5)
ccd_plan$yield <- yield
中身を確認すると、yieldという項目が追加されている事が確認できますね。
> ccd_plan
run.order std.order Time Temp Block yield
1 1 1 80.00000 170.0000 1 80.5
2 2 2 90.00000 170.0000 1 82.0
3 3 3 80.00000 180.0000 1 81.5
4 4 4 90.00000 180.0000 1 83.5
5 5 5 85.00000 175.0000 1 83.9
6 6 6 85.00000 175.0000 1 84.3
7 7 7 85.00000 175.0000 1 84.0
8 1 1 77.92893 175.0000 2 75.6
9 2 2 92.07107 175.0000 2 78.4
10 3 3 85.00000 167.9289 2 77.0
11 4 4 85.00000 182.0711 2 78.5
12 5 5 85.00000 175.0000 2 79.7
13 6 6 85.00000 175.0000 2 79.8
14 7 7 85.00000 175.0000 2 79.5
Data are stored in coded form using these coding formulas ...
x1 ~ (Time - 85)/5
x2 ~ (Temp - 175)/5
モデルの作成
rsm関数にデータを渡せば良いです。SOはSecond orderの略で、二次関数であてはめますよ、という意味です。ここをFOにするとFirst orderつまり一次関数であてはめる事になります。
res1 <- rsm(formula = yield ~ SO(x1, x2), data = ccd_plan)
summary関数で結果を確認します。
> summary(res1)
Call:
rsm(formula = yield ~ SO(x1, x2), data = ccd_plan)
Estimate Std. Error t value Pr(>|t|)
(Intercept) 81.86667 1.20518 67.9292 2.455e-12 ***
x1 0.93247 1.04371 0.8934 0.3977
x2 0.57767 1.04371 0.5535 0.5951
x1:x2 0.12500 1.47603 0.0847 0.9346
x1^2 -1.30833 1.08633 -1.2044 0.2629
x2^2 -0.93333 1.08633 -0.8592 0.4153
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Multiple R-squared: 0.2827, Adjusted R-squared: -0.1656
F-statistic: 0.6306 on 5 and 8 DF, p-value: 0.6827
Analysis of Variance Table
Response: yield
Df Sum Sq Mean Sq F value Pr(>F)
FO(x1, x2) 2 9.626 4.8128 0.5523 0.5961
TWI(x1, x2) 1 0.063 0.0625 0.0072 0.9346
PQ(x1, x2) 2 17.791 8.8957 1.0208 0.4029
Residuals 8 69.718 8.7147
Lack of fit 3 40.544 13.5148 2.3163 0.1928
Pure error 5 29.173 5.8347
Stationary point of response surface:
x1 x2
0.3723341 0.3343965
Stationary point in original units:
Time Temp
86.86167 176.67198
Eigenanalysis:
eigen() decomposition
$values
[1] -0.923191 -1.318476
$vectors
[,1] [,2]
x1 -0.1601822 -0.9870875
x2 -0.9870875 0.1601822
係数のPrが高いな、、、となりますね。Blockを入れて再度モデルを作成してみましょう。
res2 <- rsm(formula = yield ~ Block + SO(x1, x2), data = ccd_plan)
> summary(res2)
Call:
rsm(formula = yield ~ Block + SO(x1, x2), data = ccd_plan)
Estimate Std. Error t value Pr(>|t|)
(Intercept) 84.095238 0.079594 1056.5488 < 2.2e-16 ***
Block2 -4.457143 0.087191 -51.1192 2.871e-10 ***
x1 0.932475 0.057672 16.1687 8.420e-07 ***
x2 0.577665 0.057672 10.0165 2.116e-05 ***
x1:x2 0.125000 0.081560 1.5326 0.1692
x1^2 -1.308333 0.060026 -21.7960 1.080e-07 ***
x2^2 -0.933333 0.060026 -15.5487 1.100e-06 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Multiple R-squared: 0.9981, Adjusted R-squared: 0.9964
F-statistic: 607.7 on 6 and 7 DF, p-value: 3.801e-09
Analysis of Variance Table
Response: yield
Df Sum Sq Mean Sq F value Pr(>F)
Block 1 69.531 69.531 2613.1731 2.871e-10
FO(x1, x2) 2 9.626 4.813 180.8785 9.424e-07
TWI(x1, x2) 1 0.063 0.063 2.3489 0.1692
PQ(x1, x2) 2 17.791 8.896 334.3220 1.132e-07
Residuals 7 0.186 0.027
Lack of fit 3 0.053 0.018 0.5292 0.6859
Pure error 4 0.133 0.033
Stationary point of response surface:
x1 x2
0.3723341 0.3343965
Stationary point in original units:
Time Temp
86.86167 176.67198
Eigenanalysis:
eigen() decomposition
$values
[1] -0.923191 -1.318476
$vectors
[,1] [,2]
x1 -0.1601822 -0.9870875
x2 -0.9870875 0.1601822
Prがだいぶ下がりましたね。私はざっくり以下のことを確認します。
- 各係数とPrを確認を確認しどの係数が有効そうかを確認する。今回は
x1:x2以外はまあ有効そうだ、と考えて良いかと思います。 - 分散分析のテーブルから、有効そうな計算式を読み取ります。今回は
TWI(x1, x2)以外は有効そうかな、と考えてよいかと思います。TWI(x1, x2)は相互作用ですを示します。 - Stationary pointから最適値を見ます。この時、固有値が両方ともマイナスになっているので、各因子とも上に凸、つまりStationary pointで最大値を取ることが読み取れます。
eigen() decomposition
$values
[1] -0.923191 -1.318476
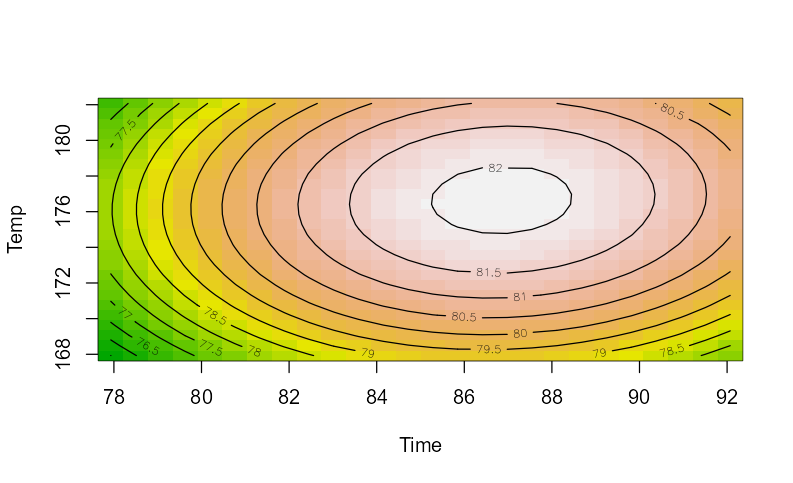
最後に等高線を確認してみましょう。
contour(res2,
~ x1 + x2,
image = TRUE,
at = summary(res2)$canonical$xs)
Timeが87, Tempが176あたりで最大を取っていることが確認できますね。あとは現場判断で、最大値が望める所で一度処理して様子を見るとか、そんな流れになっていくのかと思われます。
まとめ
Rで実験計画法、今回は特に応答曲面法でモデルを作成するやり方について見ていきました。
今回のモデルでは固有値が両方ともマイナスになっているので悩むことは少ないですが、片方がプラスで片方がマイナスになる場合もあります。この場合は鞍点と呼ばれ単純にStationary pointを選択すれば良いとはならず、等高線とにらめっこしながらどの条件を選択する必要があるかを考える必要があります。これについては、別の機会に整理したいと思います。
Rでの実験計画法については、様々なライブラリはあるのですが日本語で解説したものが少ないため、今後も頑張って書いていきたいところですね。