公平なあみだくじって何回横線を引けばいいの？

あみだくじの公平性

あみだくじは公平でないことで有名ですが，
できるだけ"公平らしく"行うにはどうすれば？ということで調査。

パラメータとしていじれるのは縦線数，横線数くらいですかね。
今回は横線の数であみだくじがどう変化するのか見る。

あみだくじの定義

あみだくじの中身の部分を定義する。
横線の数（N_vertical）分，要素をランダムに入れ替えるだけ。
行いたいシミュレーションの特性上，初期値を以下のように設定。

GL_start = np.arange(N_vertical) #あみだくじ初期値
#print(GL_start) #縦線8本の場合
#[1,2,3,4,5,6,7,8]

def GhostLeg(GL_start, N_horizontal):

    for i in range(N_horizontal):        
        attention = np.random.randint(N_vertical) #横線位置
        if attention == 0:
            GL_start[0], GL_start[1] = GL_start[1], GL_start[0]
        elif attention == N_vertical-1:
            GL_start[-1], GL_start[-2] = GL_start[-2], GL_start[-1]
        else:
            which = np.random.choice([-1, 1]) #左右どちらと交換するか選択
            GL_start[attention], GL_start[attention + which] = GL_start[attention + which], GL_start[attention]
    return GL_start

シミュレーション

今回は縦線8本で固定して，”横線何本あれば公平なの？”をシミュレーションしてみる。
どこのスタート地点を選んでも，移動距離（スタート地点からどれだけ離れた地点にゴールしたか）が同じになれば，ひとまず公平と言えるかもしれない。
したがって，横線の数を増やしていき，それぞれの移動距離の信頼区間をとることにする。

それぞれの横線数ごとに，10回試行の移動距離平均を100回出して，信頼区間を出す。
グラフ表示部分は割愛。

N_vertical = 8 #縦線の数
Ntrial = 10 #試行回数
Nsample = 100 #標本数
const = 0

for i in range(len(N_horizontal)): #横線の数を変化
    for sampleIte in range(Nsample): 
        for trialIte in range(Ntrial):

            GL_temp = copy.deepcopy(GL_start) #あみだくじ初期化
            GL_end = GhostLeg(GL_temp, N_horizontal[const])

            #移動距離の平均
            for moveIte in range(1, N_vertical+1):
                tmp = list(GL_end).index(moveIte)
                GL_goal[moveIte-1] = tmp + 1 #ゴール地点がどこか（引数+1）
            movements_mean = np.mean(abs(GL_goal - GL_start))

        GL_result[sampleIte, i] = movements_mean
    const = const + 1

結果

愚直なプログラムでしたが，結果はとりあえず出ました。

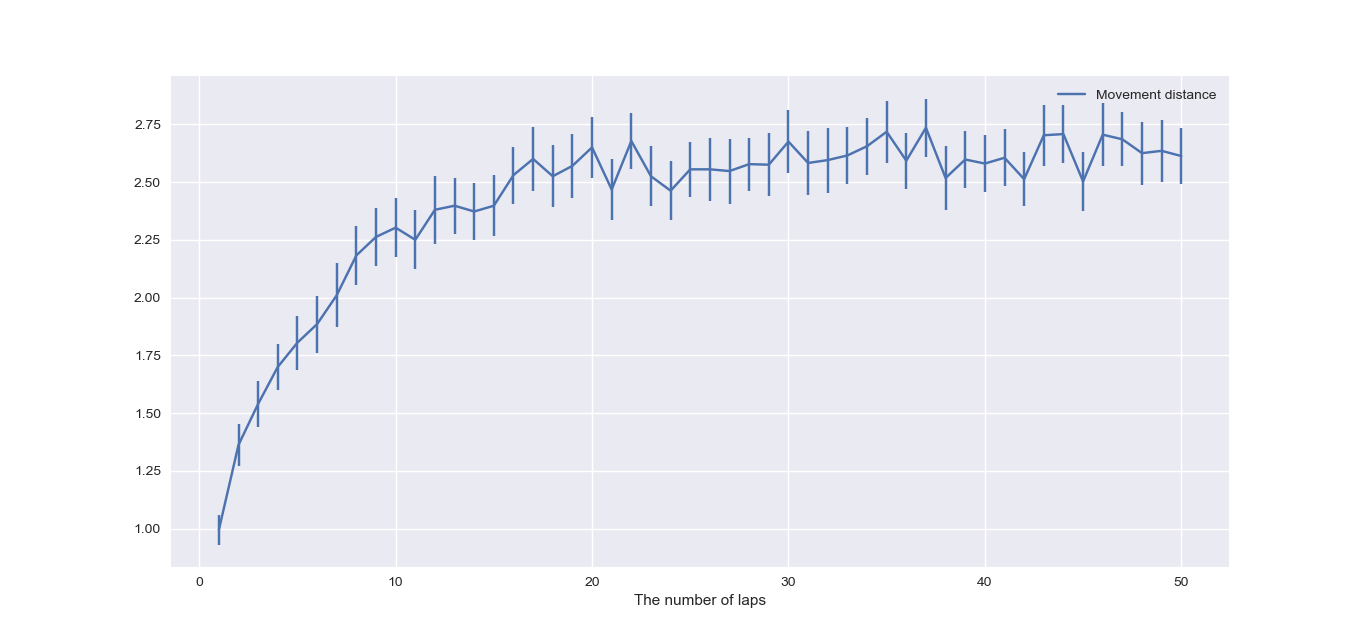
横軸は単純な横線数でなく，8人で1回ずつ線を引く動作を何周したかを表します。
これを見ると，およそ16周以降で移動距離が2.50~2.75に収束します。

8人のあみだくじを公平にするには，最低16周，128本の横線を引きましょう。
うーん，多いな！

しかし，選んだところから2,3本離れたところにしか行けないので
当たりから近い棒を選ぶのがやはり無難でした。