機械学習
0.事前準備
Google Colaboratoryとは?
•クラウドで実行されるJupyterノートブック環境
•設定不要
•無償利用が可能
•ブラウザからの利用
•コードの記述と実行
•解析の保存・共有
•強力なコンピューティングリソースへのアクセス
1.機械学習
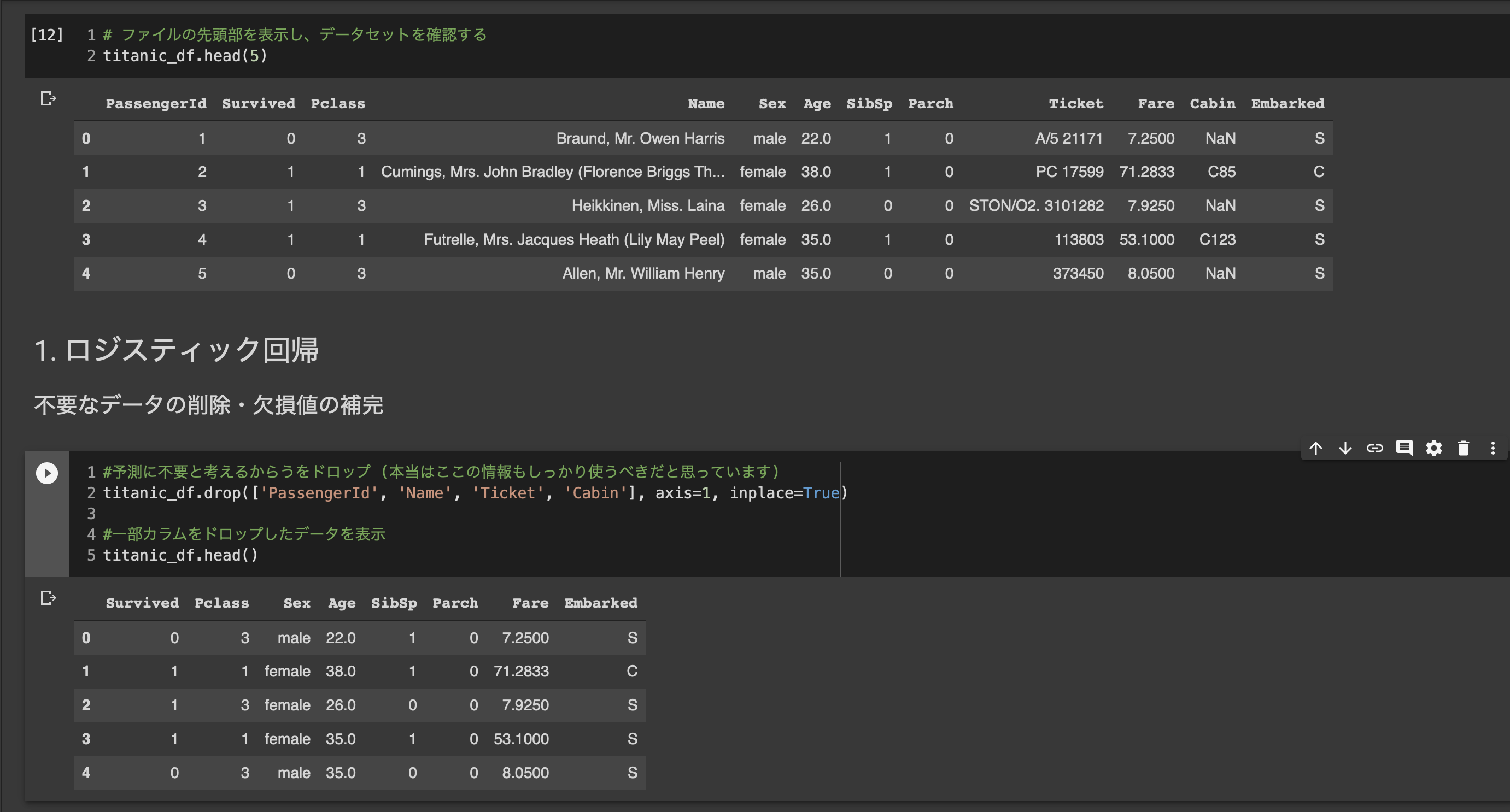
・機械学習モデリングプロセス
問題設定→データ選定→データの前処理→機械学習モデルの選定→モデルの学習→モデルの評価
・機械学習
コンピュータプログラムは、タスクT(アプリケーションにさせたいこと)を性能指標Pで測定し、その性能が経験E(データ)により改善される場合、タスクTおよび性能指標Pに関して経験Eから学習すると言われている(トム・ミッチェル1997)
$ $
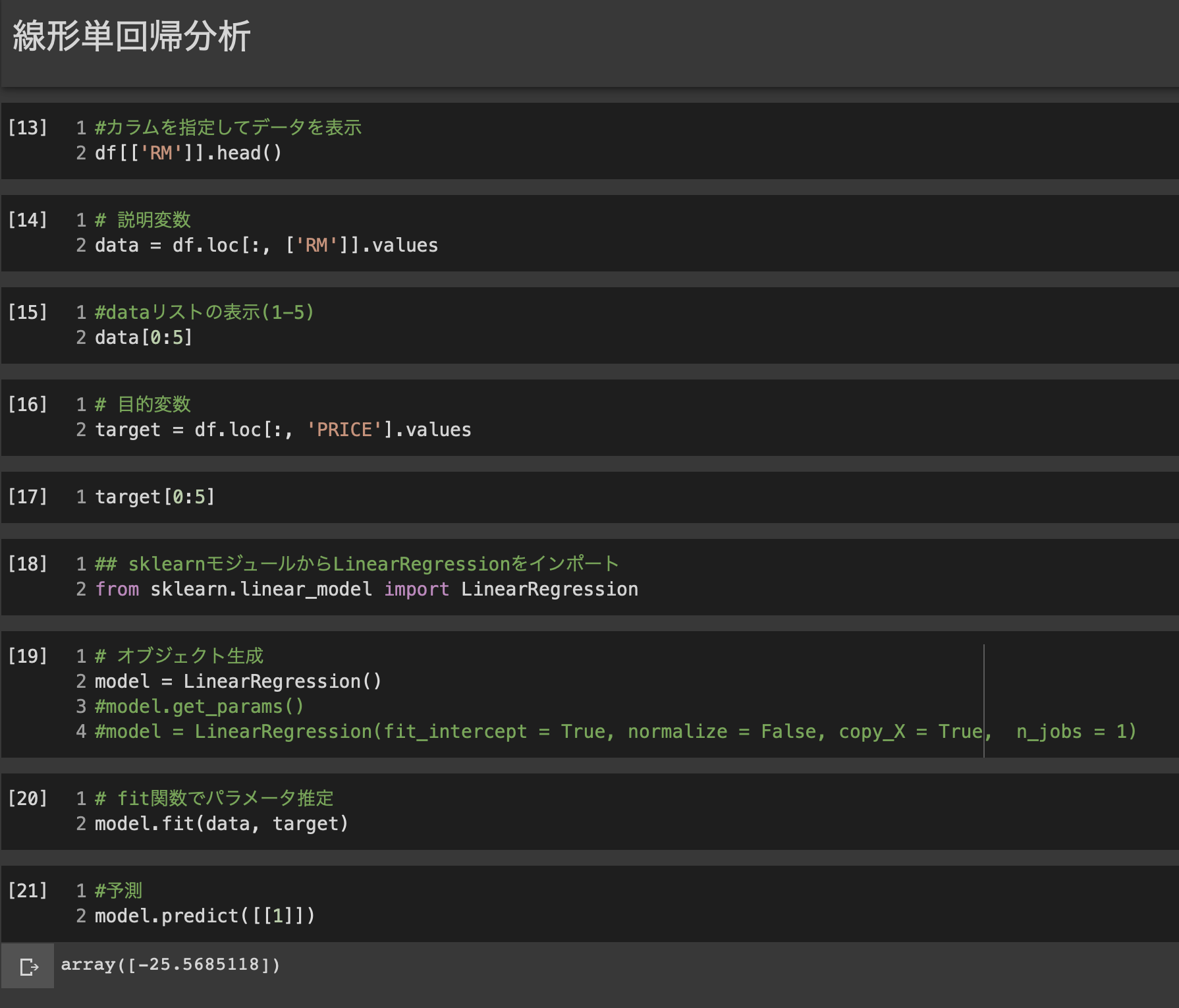
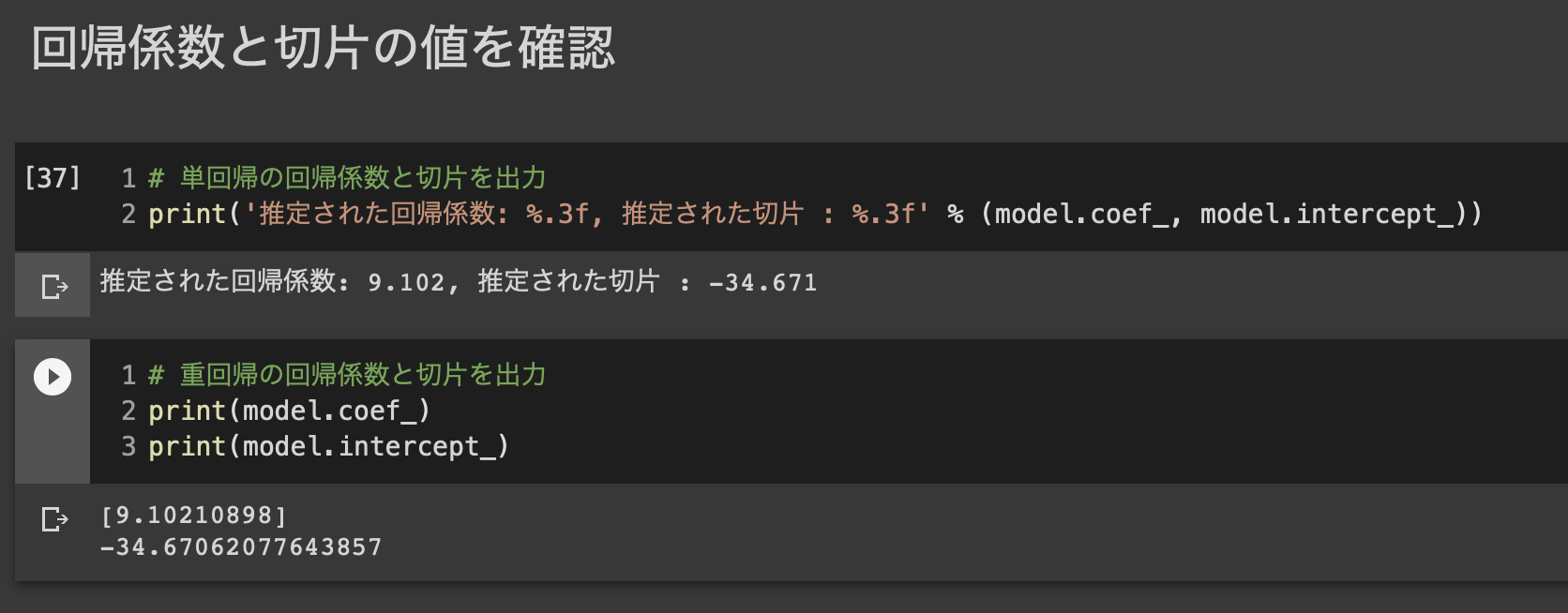
■線形回帰モデル
・入力とm次元パラメータの線形結合を出力するモデル
慣例として予測値にはハットを付ける(正解データとは異なる)
・パラメータwは最小二乗法により推定する。
$(W_0:切片、w^T:回帰係数)$
$・\hat{Y}とYの誤差はεを用いて表す。$
・m次元パラメータ
$\ w = (w_1,w_2,…w_m)^T ∈ R^m$
・線形結合
$\hat{Y} = w^Tx + w_0 =\sum_{j=1}^{m}w_jx_j + w_0$
①データの選定について
データは学習用と検証用に分割する必要がある。
理由:性能測定では未知のデータに対する精度の高さを測定するため
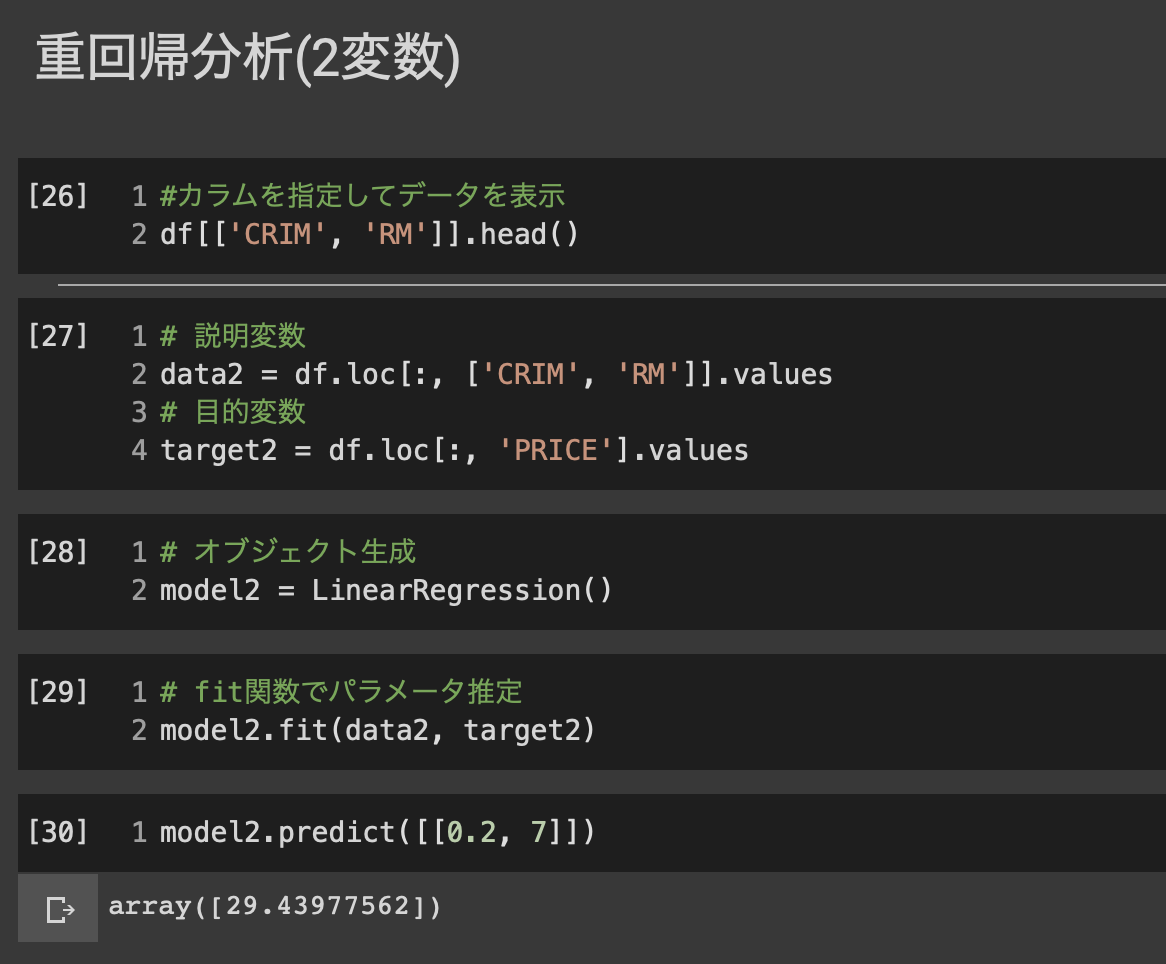
②最小二乗法
・学習データの平均二乗誤差を最小とするパラメータを探索する方法
・最小値を求めるには、平均二乗誤差を微分してその勾配が0になる点を求めれば良い
回帰係数
$\hat{w} = (X^{(train)T}X^{(train)})^{-1}X^{(train)T}y^{(train)}$
■非線形回帰モデル
データ構造を線形モデルでとらえる場面は限られるため、非線形で考える必要がある。
未知パラメータの求め方は線形回帰モデルと同じ(最小二乗法、最尤法)
回帰関数には基底関数と呼ばれる既知の非線形関数とパラメータベクトルの線型結合を使用
①主な基底関数
多項式関数(例:$φ_j=x^j$)
ガウス型基底関数
スプライン関数/ Bスプライン関数
②未学習と過学習
未学習:学習データに対して誤差が大きい。
過学習:学習データに対して誤差が小さい。検証や本番データを使用時に誤差が大きくなる。
③正則化法
モデルが複雑になりすぎないように罰則項を設けること
Ridge推定:パラメータを0に近づけるように推定
Lasso推定:いくつかのパラメータを正確に0に推定
④モデル選択
未学習や過学習を回避するためにはテスト誤差と小さくする必要がある
ホールドアウト法
データを学習用とテスト用に分割する方法。大量データ以外では性能評価が低い
クロスバリデーション(交差検証)法
データを5分割し都度検証データを変え、5回に分けて評価を行う。全データに使用可能
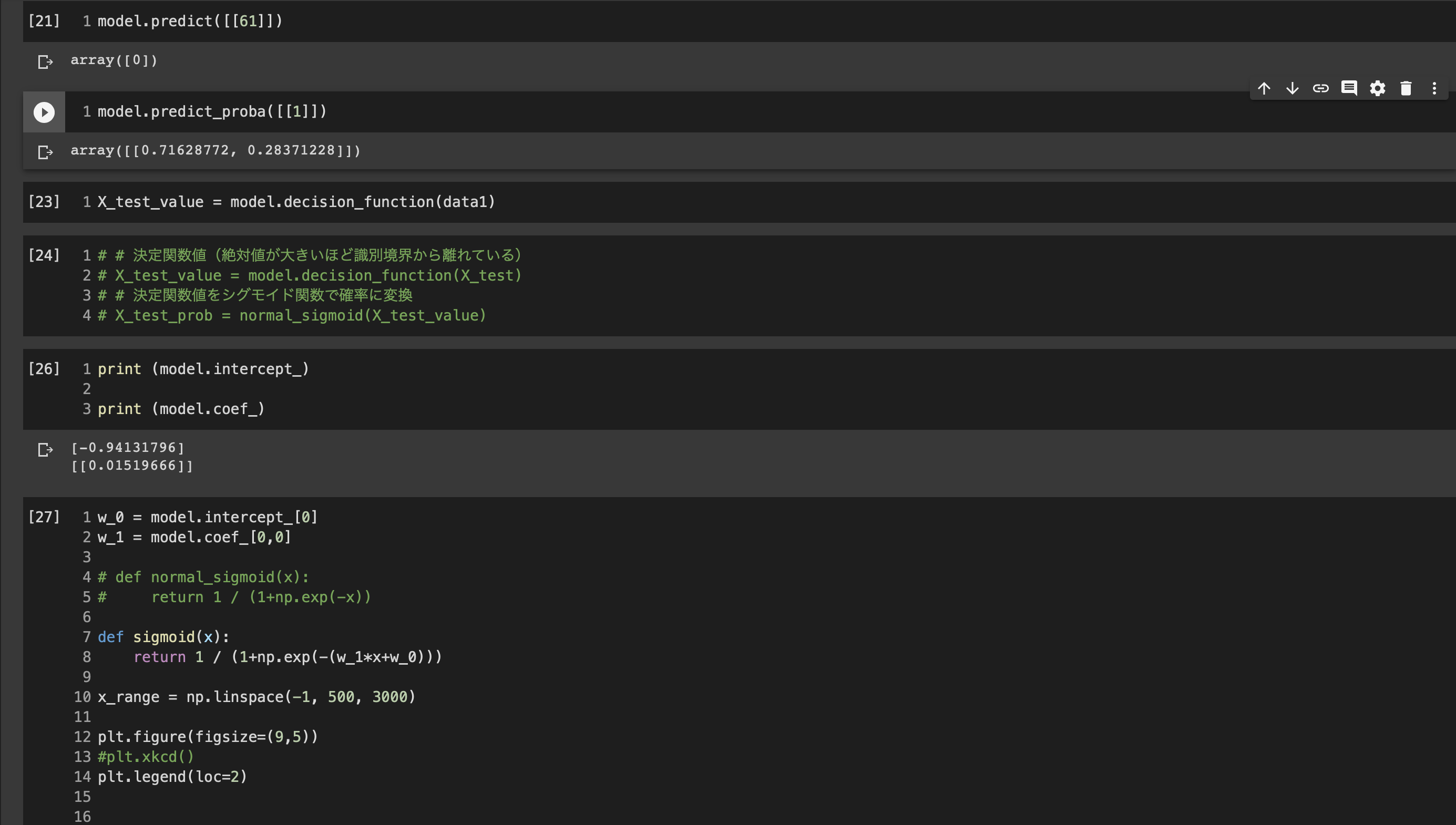
■ロジスティック回帰モデル
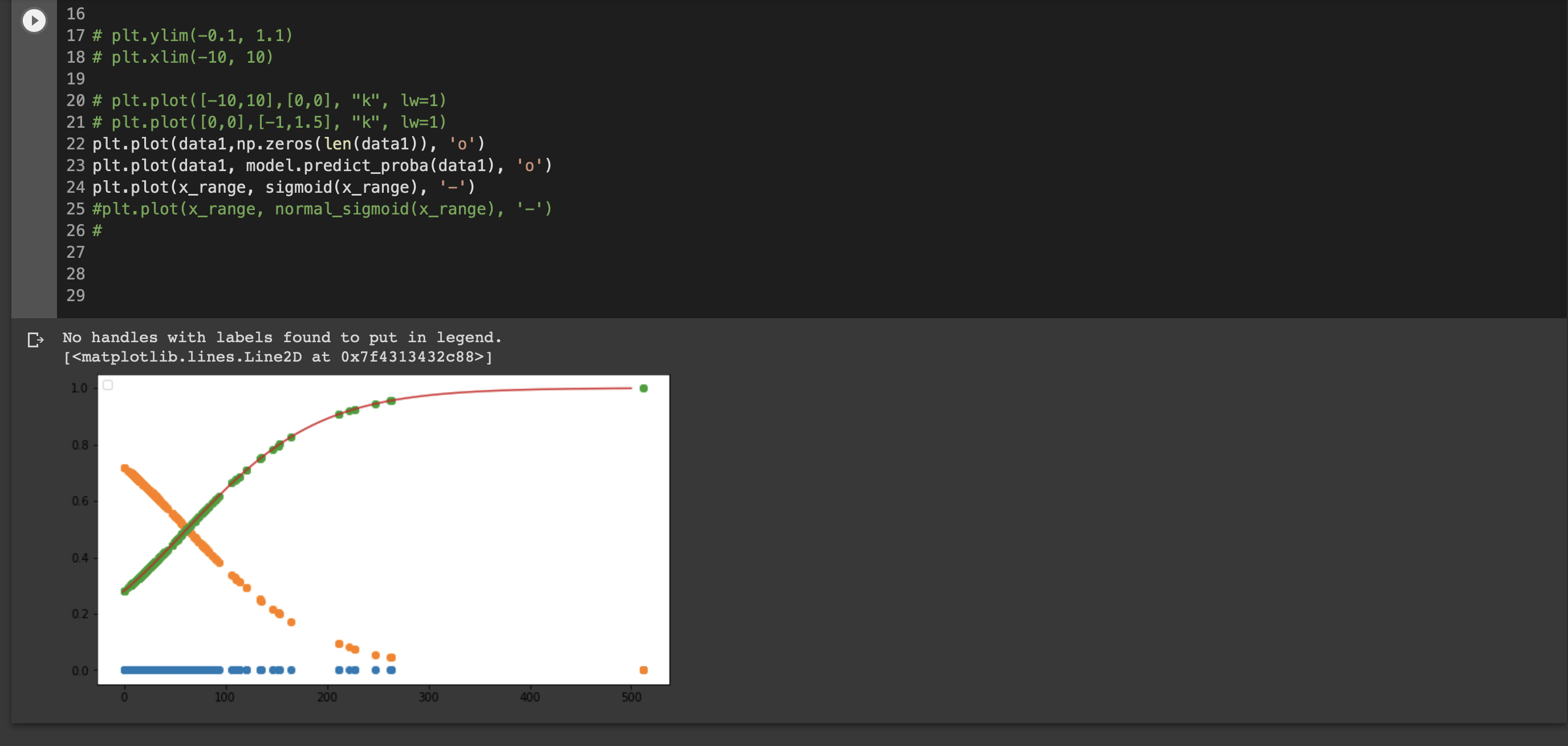
ロジスティック回帰はクラスに分類するための問題
ある値が0.5位受の場合は1、0.5未満の場合は0と判断する。
その際にシグモイド関数を使用する。
ベルヌーイ分布を使用する。
①シグモイド関数
単調増加の関数。実数を入力することで0~1の値を出力する。
②最尤推定
尤度関数が最大となるようなパラメータを探索する方法
計算を簡略化するため対数を利用する。(対数尤度関数)
③勾配降下法
反復学習によりおパラメータを逐次的に学習する方法の一つ
最尤推定では対数尤度関数をパラメータで微分して0になる値を求める必要があるが
解析的にこの値を求めることが困難であるためこの方法を用いる。
④確率勾配降下法
勾配降下法ではデータ更新時に全てのデータを更新する必要があるためメモリや時間を要する。
そのため更新するデータを確率的に選択するこの方法が用いる。
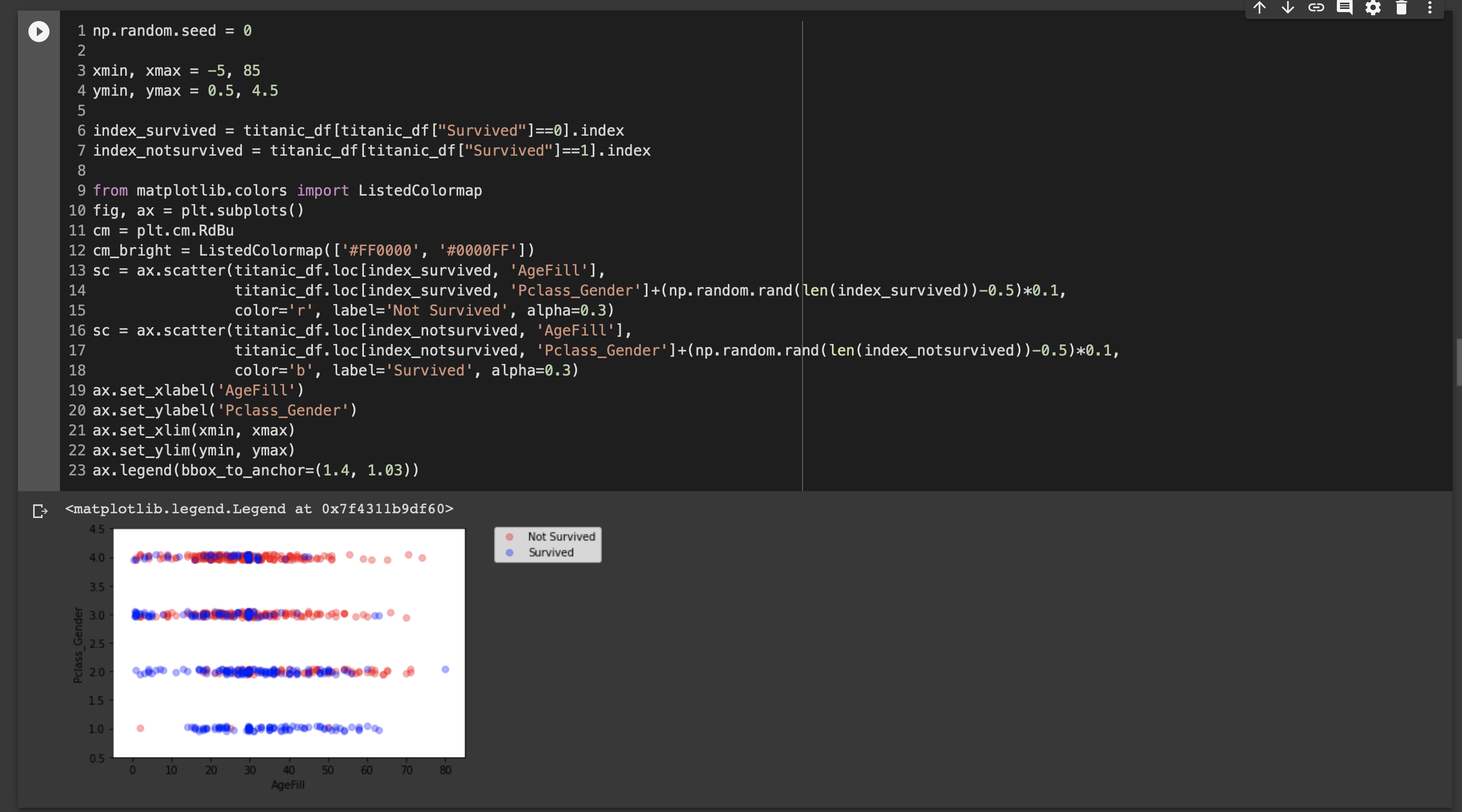
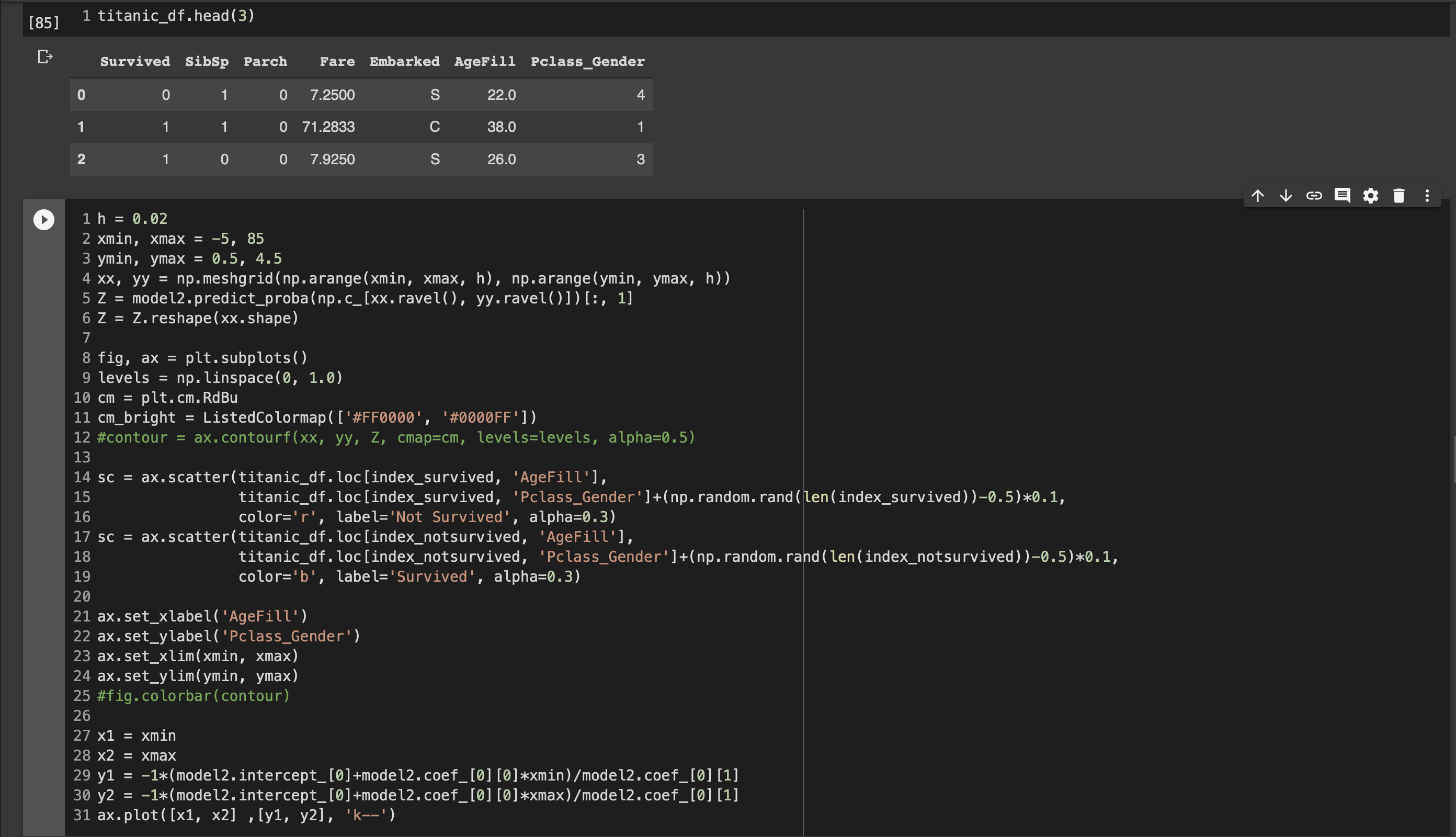
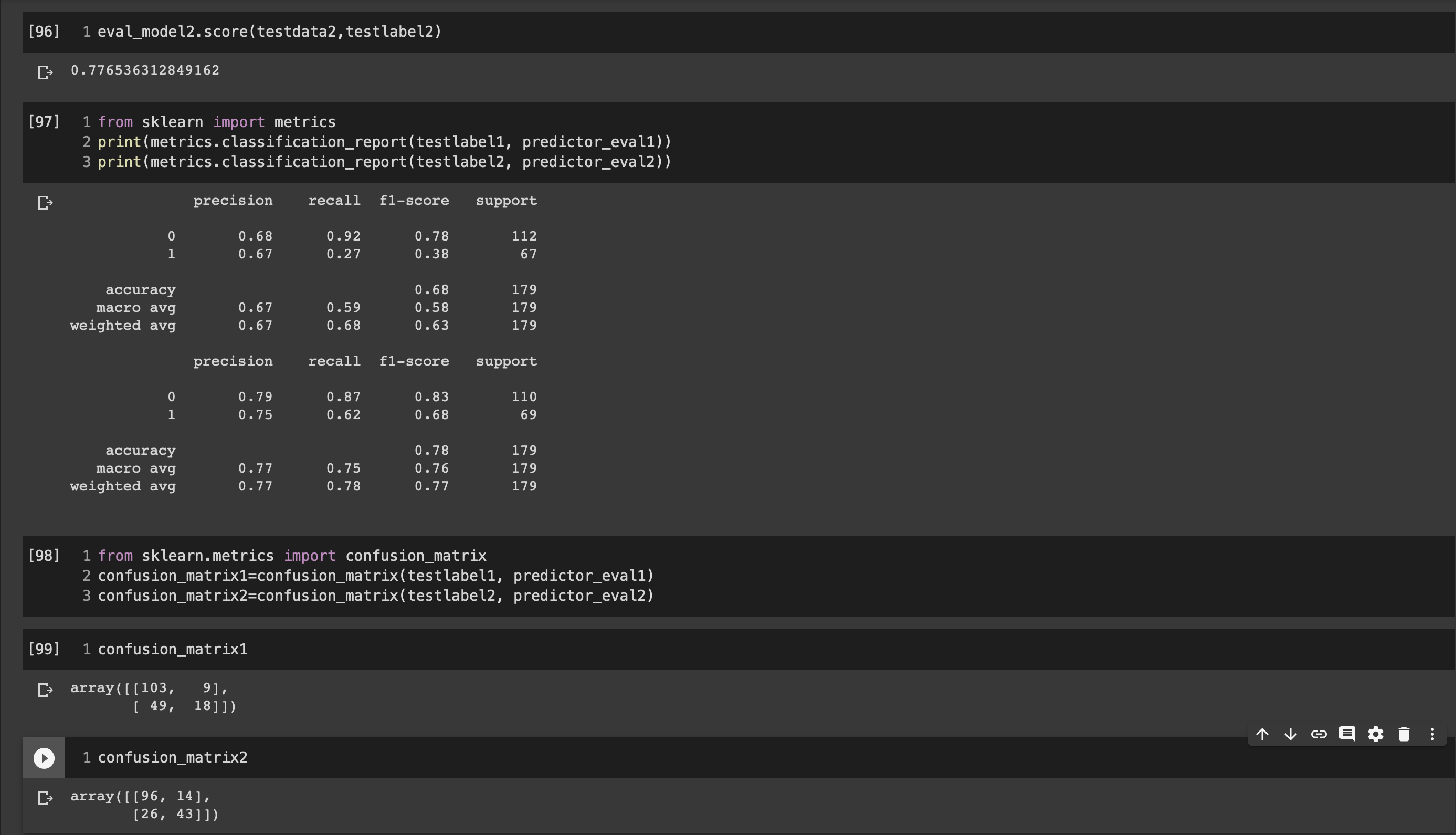
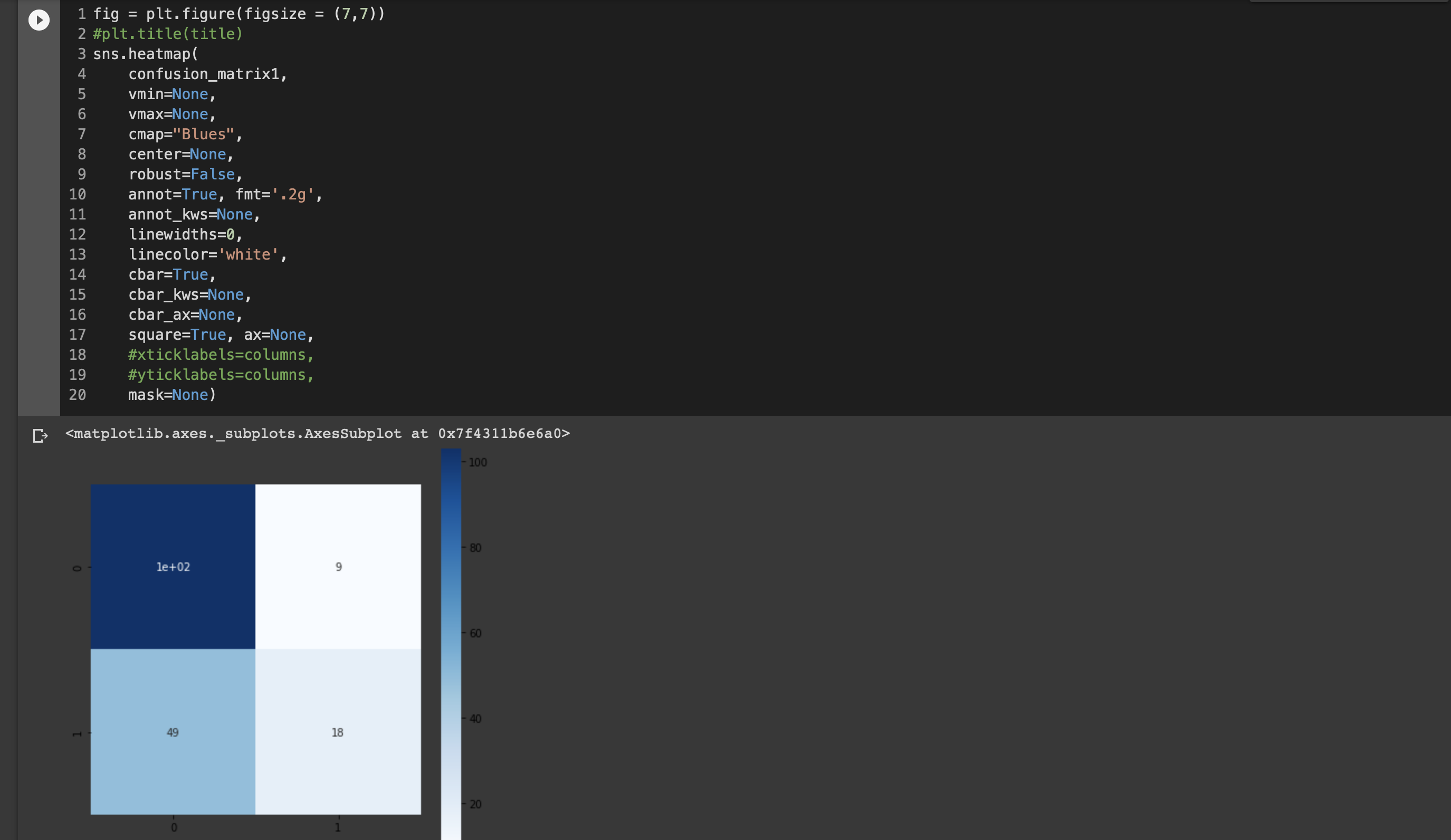
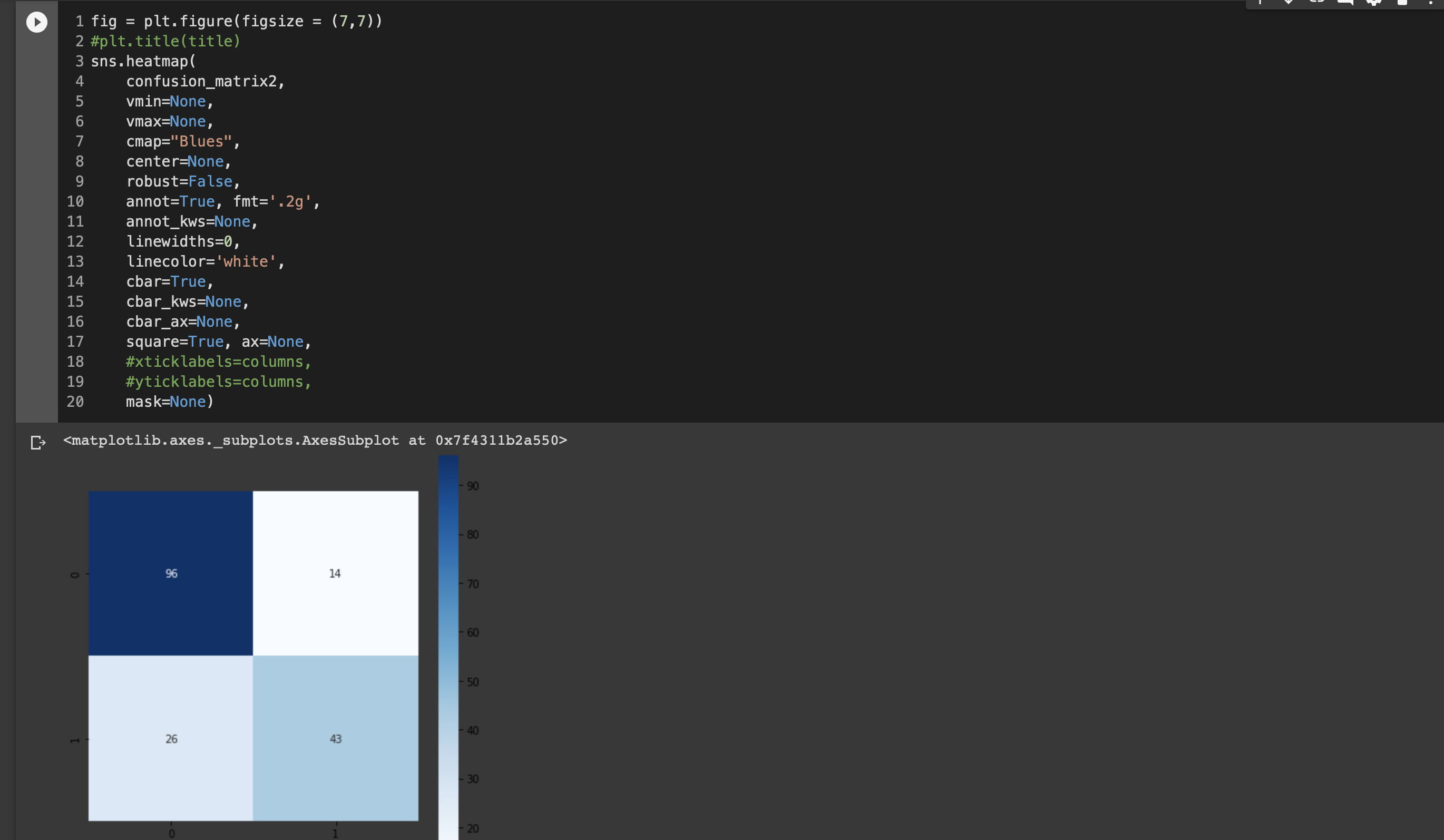
⑤モデルの評価
モデルの予測結果と検証ようデータの結果をそれぞれnegative/positiveで表す。
指標1;正解率 (それだけでは不足のため以下2つも重視する)
指標2:再現率 (例)癌検査
指標3:適合率 (例)スパムメール





■主成分分析
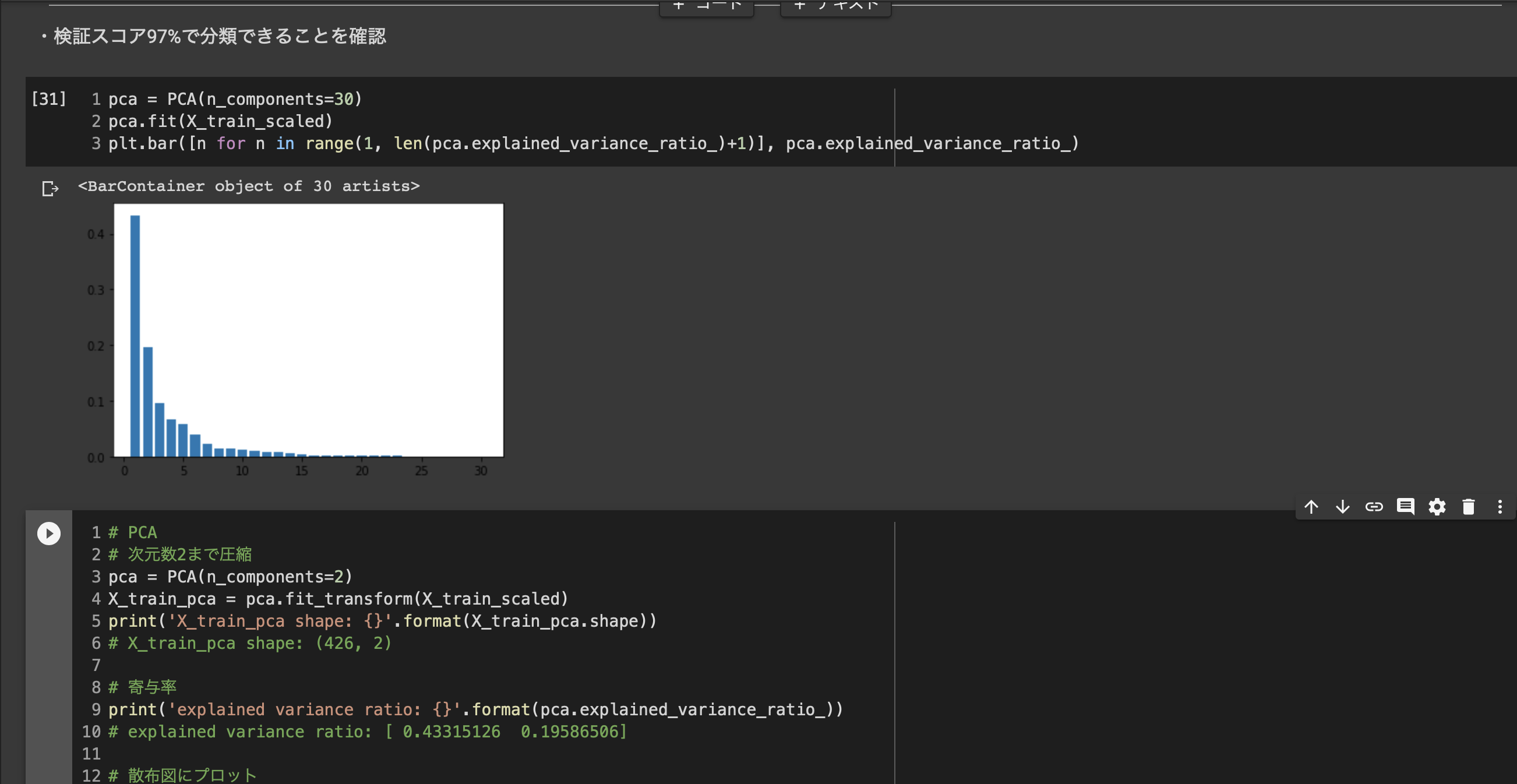
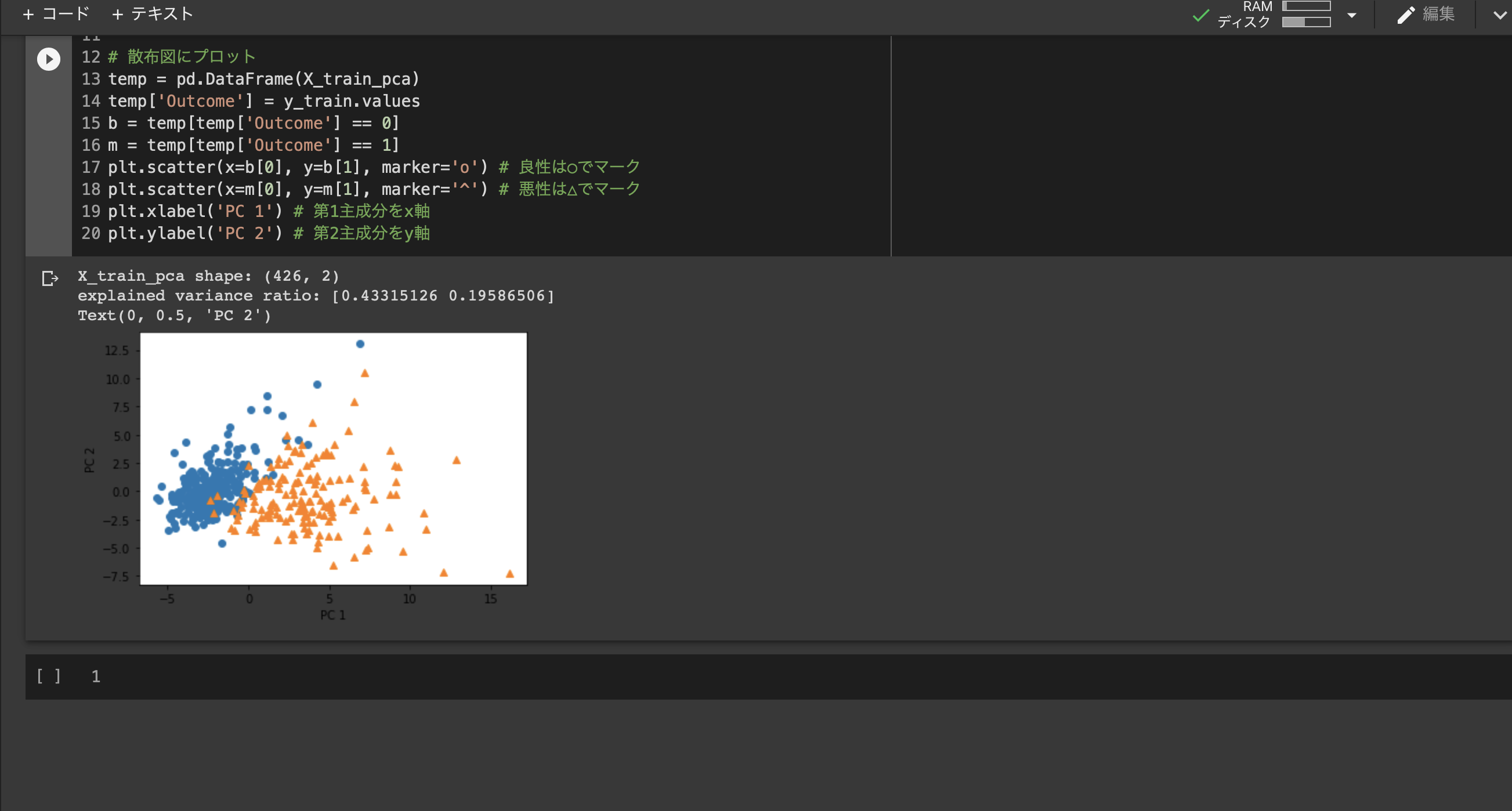
情報の損失を最小限にしたまま次元を圧縮する方法
→情報の損失を判断するには変換後の分散の値を確認すれば良い。(最大となる場合を求める)
■制約付き最適化問題の解き方
ラグランジュ関数を最大にするを探索する。(微分して0になる点)
解:$Var(\bar{X})a_j = λa_j$
■寄与率
第1~元次元分の主成分の分散は、元のデータの分散と一致
■ハンズオン3


■k近傍法
最近傍のデータをk個取得し、それらが最も多く所属するクラスに識別する。
kを大きくすると決定境界が滑らかになる。
■k-平均法
教師なし学習
クラスタリング手法
与えられたデータをkこのデータに分類する
以上