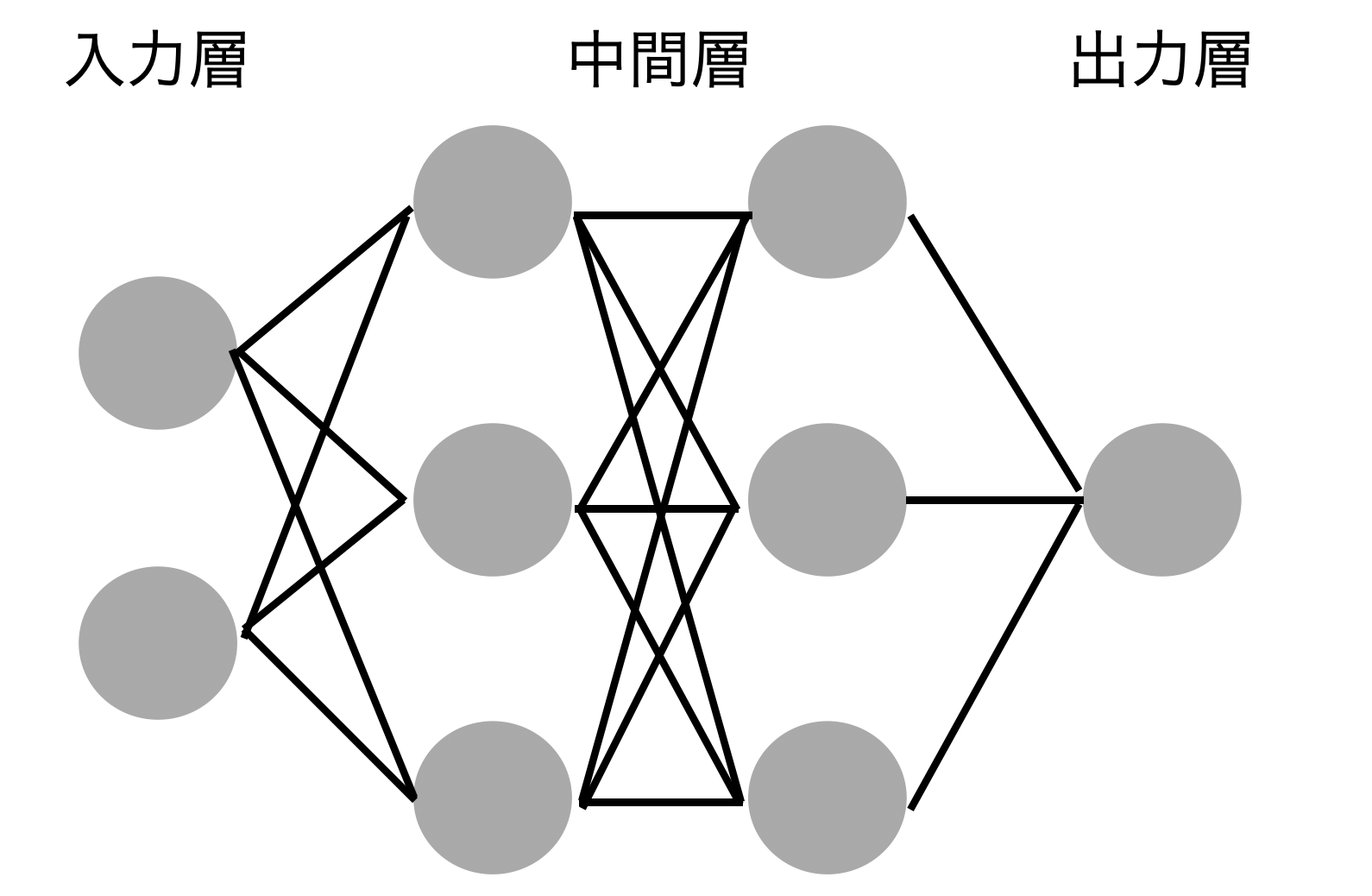
深層学習day1
本レポートでは講義のまとめと問題の解答を記載する。 問題とその解答については下記のように示す。 (問:問題、答:筆者の答案、解:教材の模範解答)0.全体像
■ニューラルネットワーク問:ディープラーニングは結局何をやろうとしているのか
答:人間の脳であるニューロンを真似ることで、機械にも画像や音声のデータを判別すること
解:誤差を最小化するパラメータを発見すること
問:どの値の最適化が最終目的か
答:バイアス
解:重み、バイアス
■ニューラルネットワーク(NN)でできること
回帰
連続する実数値をとる関数の近似
例:結果予想、ランキング
回帰分析の種類
・線形回帰
・回帰木 など
分類
性別(男あるいは女)や動物の種類など離散的な結果を予想するための分析
例:写真の判別、文字認識
分類分析の種類
・ベイズ分類
・ロジスティック回帰
・決定木 など
深層学習の実用例
自動売買(トレード)
チャットボット
翻訳 など
1.入力層〜中間層
入力:$x_i$ 重み:$w_i$ バイアス:b 総入力:u 出力:z 活性化関数:f 入力層のインデックス:i 数式:$u = w_1x_1 + w_2x_2 + ... + w_ix_i + b$ $= Wx + b$ ⇨(Pythonで記載する場合) u1 = np.dot(x, W1) + b1問:1-1のファイルから
中間層の出力を定義しているソースを抜き出せ
答、解:z = functions.relu(u)
2.活性化関数
■活性化関数 ニューラルネットワークにおいて次の層の出力の大きさを決める非線形の関数■中間層用の活性化関数
・ReLU関数
→現在最も使われている関数。勾配消失問題が回避できる。
・シグモイド(ロジスティック)関数
→0~1を緩やかに変化する関数。人間的。勾配消失問題がある。
・ステップ関数
→出力は常に1か0。機械的
■出力層用の活性化関数
ソフトマックス関数
恒等写像
シグモイド関数(ロジスティック関数)
入力:$x_i$
重み:$w_i$
バイアス:b
総入力:u
出力:z
活性化関数:f
入力層のインデックス:i
第二層のインデックス:j
u = Wx
z = f(u)
問:配布されているソースより z = f(u) に該当するソースを抜き出せ
答、解:z1 = functions.sigmoid(u)
3.勾配降下法
■深層学習の目的 学習を通して誤差を最小にするネットワークを作成すること →誤差E(x)を最小化するパラメータwwp発見すること →勾配降下法を利用してパラメータを最適化 $w^{(t+1)} = w^{t} - ε$▽$E$(ε:学習率)
・学習率が大きすぎた場合→発散してしまい、最初値が見つからない
・学習率画小さすぎた場合→発散することはないが、計算に時間がかかる
or 限られた範囲での最小値を算出してしまう可能性がある
勾配降下法の学習率の決定、収束性向上のためのアルゴリズムについては
複数の論文が公開されている。(詳しくはDay2)
■確率的勾配降下法(SGD)
式は勾配降下法と変わらないが、アプローチが異なる。
確率勾配降下法:ランダムに抽出したサンプルの誤差
勾配降下法:全サンプルの平均誤差
メリット
・データが冗長な場合の計算コストが軽減できる
・望まない局所極小会に収束するリスクの軽減
・オンライン学習ができる
問:オンライン学習とは何か
答、解:学習データが追加されるたび、追加分のデータを用いて学習を行うこと。
■ミニバッチ勾配降下法
式は勾配降下法と変わらないが、アプローチが異なる。
ミニバッチ勾配降下法:ランダムに分割したデータの集合に属するサンプルの平均誤差
勾配降下法:全サンプルの平均誤差
確率勾配降下法のメリットを損なわずに、計算機の計算資源を有効利用できる
→CPUを利用したスレッド並列化やGPUを利用したSIMD並列化
■誤差勾配の計算 - 数値微分
プログラムで微小な数値を生成し擬似的に微分を計算する一般的な手法
デメリット
・各パラメータ$W_m$それぞれについて$E(W_m+h)$と$E(W_m-h)$を
計算するために準伝播の計算を繰り返し行う必要があり負荷が大きい。
→誤差逆伝搬法を使用する。