はじめに
この記事は,某アドベントカレンダーの繋ぎ用にひねり出した記事ですが,それなりに参考になる事柄かもしれません.そのときは参考にしていただければ幸いです.
やること
以下のような,へこみが存在している多角形の全ての内角の角度をプログラムで算出する.
※座標の数字は適当です.特に意味はありません.
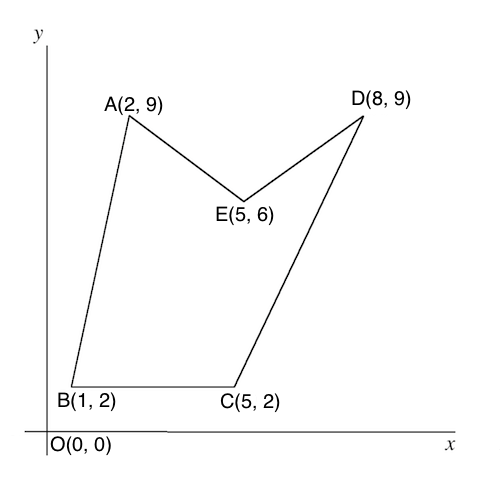
理論
角度計算式
座標平面上において,3点 $A(x_0, y_0), B(x_1, y_1), C(x_2, y_2)$ が与えられたとき,ベクトルの内積の式より,
$$ cos\theta = \frac{(x_0-x_1)(x_2-x_1)+(y_0-y_1)(y_2-y_1)}{\sqrt{(x_0-x_1)^2+(y_0-y_1)^2} \times \sqrt{(x_2-x_1)^2+(y_2-y_1)^2}}$$
と,$\angle ABC$による$cos\theta$を求めることができます.
この値よりアークコサインを計算すると,$\angle ABC$の角度$\theta$を求めることができます.
しかしそれは,角度が全て180度以下だった場合の話に限ります.例えば上の図のようなケースでは,$\angle DEA$を計算すると,算出される角度の値は外角のものとなります.人間ならば見ればわかりますが,プログラムに実装する場合は,当然なす角が180度以上か否かを判定する必要があります.
そこで使用されるのが,「三角形の符号付き面積」という概念です.
三角形の符号付き面積
3点$A(x_0, y_0), B(x_1, y_1), C(x_2, y_2)$で構成される三角形において,
$$S=\frac{1}{2}(x_0y_1+x_1y_2+x_2y_0-y_0x_1-y_1x_2-y_2x_0)$$
で与えられる値$S$を,三角形の符号付き面積と言います.
三点$A, B, C$を与えたとき,
- 求めたい内角が必ず2番目(この場合は$B$)にある.
- 点$A, B, C$が必ず反時計回りの順で与えられている.
これら二つの条件を満たしている場合,この符号付き面積$S$の値が正ならば180度以下,負ならば180度を超える角度となります.
実装
理論を踏まえてプログラム(C言語)に起こします.
なお,プログラム上でも三点$A(x_0, y_0), B(x_1, y_1), C(x_2, y_2)$を与えて角度を計算しますが,プログラム中では点$B(x_1, y_1)が(0, 0)$になるように三点の値を設定し直しています.理論での式で$x_1=0, y_1=0$となっているものが実装されています.
プログラムの解説に関しては,コメントを参照してください.
# include <stdio.h>
# include <math.h>
//x,y座標型
typedef struct point{
double x;
double y;
}Point;
//弧度法の角度から度数法へ
double rad2deg(double rad){
return rad * (180 / M_PI);
}
//角度計算関数
double angle(Point a, Point b, Point c){
int i;
double ang;
Point poly[3] = {a, b, c};
//2番目の点bを(0, 0)にし,両端点の値もそれに揃える
double tmpx = poly[1].x;
double tmpy = poly[1].y;
for(i = 0; i < 3; ++i){
poly[i].x -= tmpx;
poly[i].y -= tmpy;
}
//ベクトルの内積よりcosθを計算し,角度(0 < θ < 180)を算出
ang = acos((poly[0].x * poly[2].x + poly[0].y * poly[2].y)
/ (sqrt(pow(poly[0].x, 2) + pow(poly[0].y, 2)) * sqrt(pow(poly[2].x, 2) + pow(poly[2].y, 2))));
ang = rad2deg(ang);
//符号付き面積を計算し,符号により実際の角度が180度以下か以上かを判定
if(poly[2].x * poly[0].y - poly[0].x * poly[2].y < 0){
return 360 - ang;
}
else{
return ang;
}
}
例の図の多角形での実行結果は以下のようになりました.
∠ABC: 81.869898
∠BCD: 113.198591
∠CDE: 21.801409
∠DEA: 270.000000
∠EAB: 53.130102