feature neutralizationについて

1　この記事は

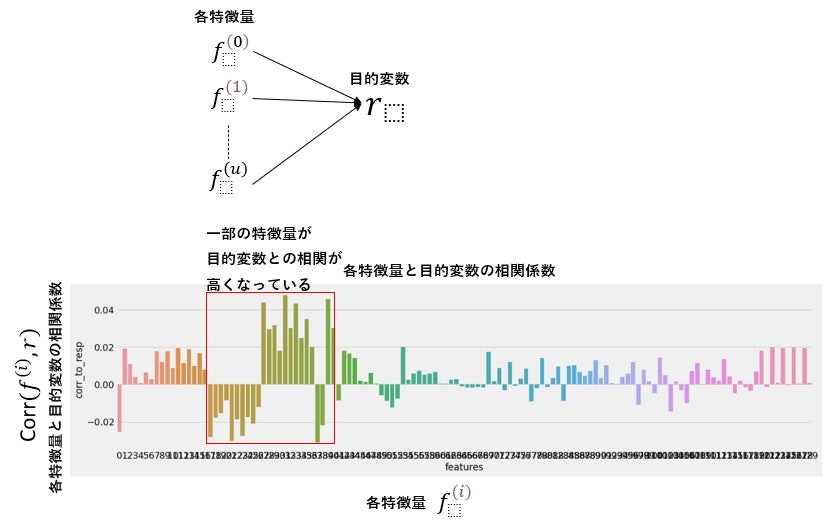
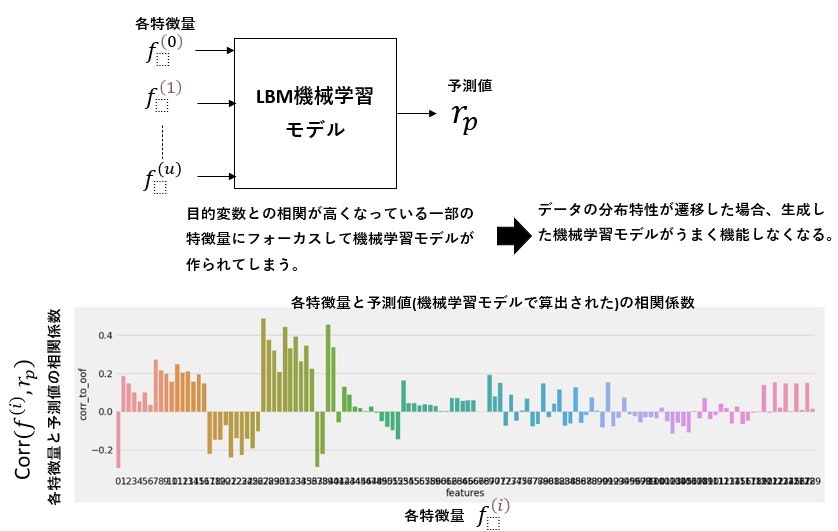
複数の特徴量を用いて目的変数を予想する機械学習モデルを構成すると、目的変数と相関係数が相対的に高い特徴量を優先して学習が行われる傾向があります。実際の運用においても前述特徴量が目的変数の予測に支配的であれば問題ないのですが、株価データのようにデータの分布特性が時期によっては遷移する場合、目的変数の予測に有効な特徴量が変化することがあります。前述現象が発生すると、生成した機械学習モデルがうまく機能しなくなります。よって、データの分布特性の変化に影響を受けない機械学習モデルを生成したく、特徴量と目的変数の相関係数を減少させるように各特徴量を変換する手法があります。前述手法は、feature neutralizationと呼ばれており、Numeraiでよく使われているとのことです。この記事では、feature neutralizationが何をやっているのか説明します。
つまり、特徴量と目的変数がどの程度相関しているか(feature exposure,特徴量が目的変数にどの程度露出しているのか)を評価し、feature exposureが小さい環境のもと、機械学習モデルを生成するという話になります)

(参照サイト)

(図1)

(図2)

2　feature neutralization

機械学習モデルの生成に使用する特徴量と目的変数の関係を下記に示します。
(図3)

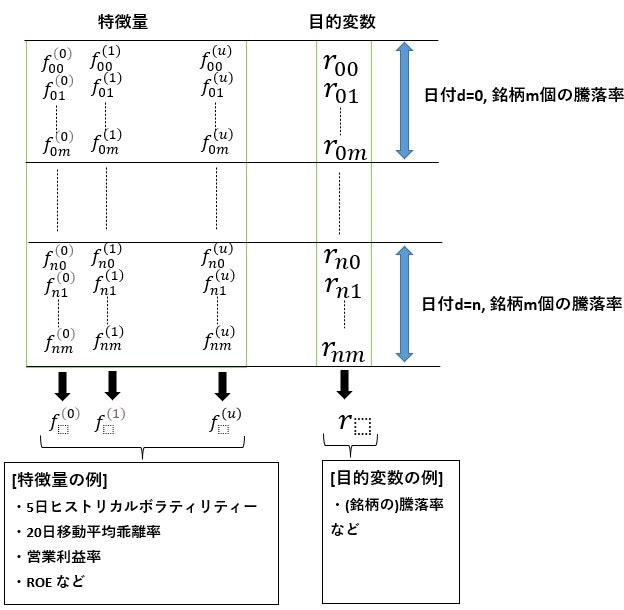
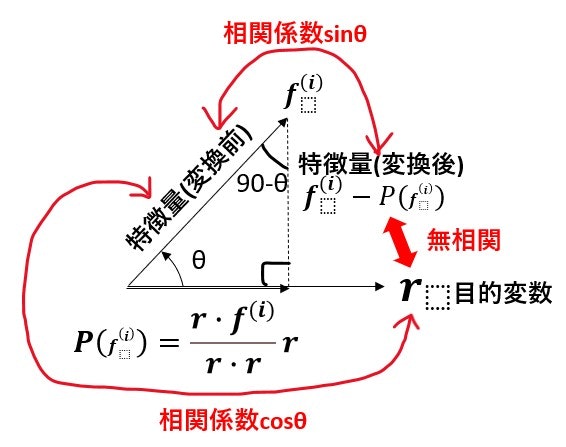
ここで、各特徴量ベクトル $\mathbf{f^{(i)}}$ を目的変数ベクトル $\mathbf{r}$に射影し、射影後のベクトルを$ P(\mathbf{f^{(i)}})$とします。
$\mathbf{f^{(i)}} - P(\mathbf{f^{(i)}})$ を新特徴量ベクトルとみなすと、新特徴量ベクトル $\mathbf{f^{(i)}} - P(\mathbf{f^{(i)}})$と 目的変数ベクトル $\mathbf{r}$は、直交する。互いのベクトルがなす角度をθとするとき2ベクトルの相関係数は、$cosθ$となる。各特徴量ベクトル $\mathbf{f^{(i)}}$と目的変数ベクトル $\mathbf{r}$の相関係数は、$cosθ$となるが、新特徴量ベクトル $\mathbf{f^{(i)}} - P(\mathbf{f^{(i)}})$と 目的変数ベクトル $\mathbf{r}$は、無相関となる。

(図4)

「変換前特徴量」と「変換後特徴量」の相関係数,「変換前特徴量」と「目的変数」　の相関係数,「変換後特徴量」と「目的変数」　の相関係数は下記の数式の通りになる。

つまり、「変換前特徴量」と「変換後特徴量」の相関係数が大きければ、「変換前特徴量」と「目的変数」　の相関係数は小さくなる。逆もしかり

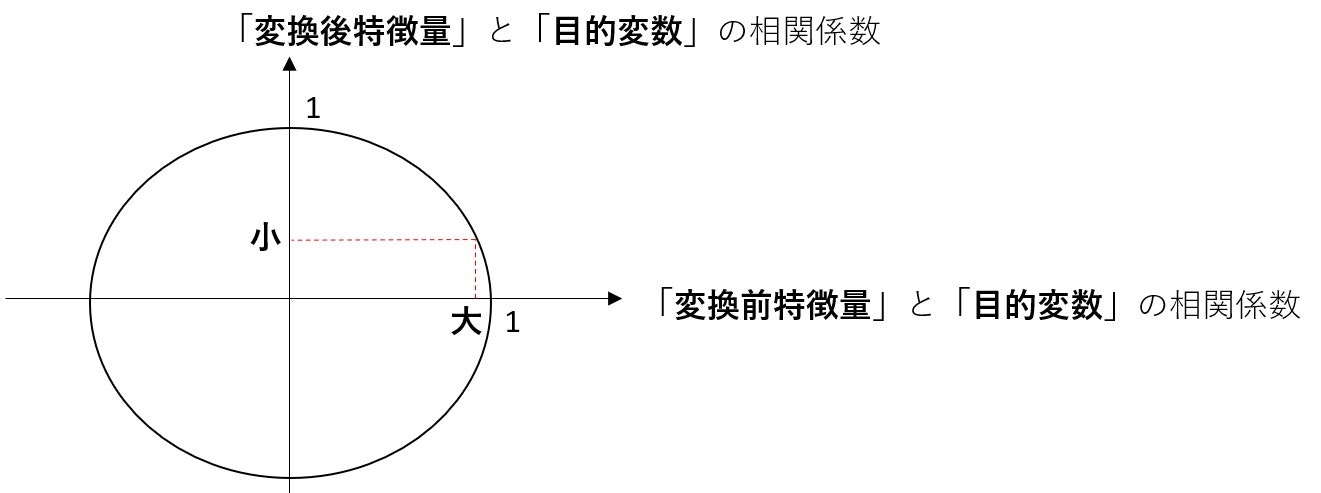
よって、「feature neutralization」を行うことにより、変換後特徴量と目的変数の相関係数を減少させられ、目的変数との相関係数が相対的に高い一部の特徴量に引っ張られる形で機械学習モデルが生成されてしまうという当初の課題であった当初の課題をクリアすることができ、より頑健性の高いモデルを作ることができる。

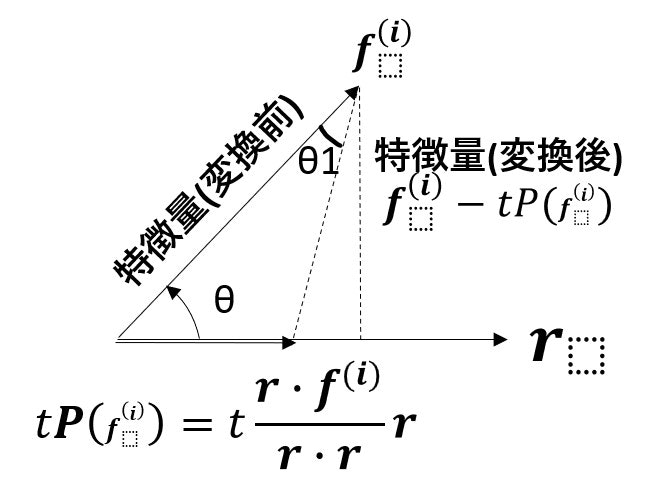
ここで、「feature neutralization」を行うと、変換前特徴量と変換後特徴量の相関係数が低くなり、変換後特徴量は、変換前特徴量が持っている情報を欠落させてしまうということも起きかねない。よって、変換前）特徴量を目的変数に射影させるとき、その射影ベクトルの大きさを小さくする(大きさの調整は変数tで行う)。変換前特徴量ベクトルと変換後特徴量ベクトルの角度θ1が小さくなることにより、変換前特徴量ベクトルと変換後特徴量ベクトルの相関係数を上げることができ、変換後特徴量に変換前特徴量の情報を入れ込むことができる。

[JaneStreet] Avoid Overfit: Feature Neutralizationには、上記で説明した「feature neutralization」を行うpythonコードが記載されています。

feature neutralize

# code to feature neutralize

import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
from tqdm.auto import tqdm

def neutralize_series(series : pd.Series, by : pd.Series, proportion=1.0):
    """
    neutralize pandas series (originally from the Numerai Tournament)
    ＊series:変換前特徴量ベクトル
    ＊by:目的変数ベクトル
    """
    scores = series.values.reshape(-1, 1)
    exposures = by.values.reshape(-1, 1)
    exposures = np.hstack((exposures, np.array([np.mean(series)] * len(exposures)).reshape(-1, 1)))
    correction = proportion * (exposures.dot(np.linalg.lstsq(exposures, scores)[0]))
    corrected_scores = scores - correction
    neutralized = pd.Series(corrected_scores.ravel(), index=series.index)
    return neutralized