#1 この記事は
ジャックベラ検定をPythonで行う方法を説明します。
#2 内容
##2-1 ジャックベラ検定とは
ジャックベラ検定とは、標本が正規分布に従うかどうかを判定する手法です。
検定統計量JBは、下記式のとおりになります。by Wikipedia
検定統計量JBはχ二乗分布に従います。検定統計量JBで下記に記載された仮設の検定を行う。(有意水準 p%)
H0(帰無仮説) : 標本は正規分布に従う。 H1(対立仮設) : 標本は正規分布に従わない。Pythonでは、 stats.jarque_bera(x)で標本xの検定統計量JBを計算できます。stats.jarque_beraの返却値は、[JB計算値, p値]です。
有意水準p=0.05に設定した場合、stats.jarque_beraの返却値p値>0.05であれば、帰無仮説が採択されるため標本は正規分布に従うと判断できます。逆に算出されたp値<=0.05の場合は、標本は正規分布に従わないと判断されます。
##2-2 Pythonでのジャックベラ検定の実行例
###例1
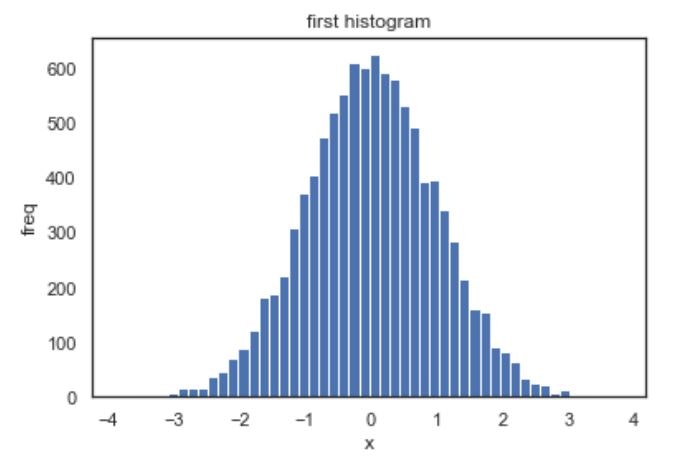
平均0,分散1の正規分布に従う乱数を10000個発生させ、標本を作製します。その標本に対してジャックベラ検定を行い、標本が正規分布に従うかを検定します。
sample.py
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
#正規分布に従う乱数を発生させる。
x = np.random.normal(0, 1, 10000)
#標本のヒストグラムを描写する。
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
ax.hist(x, bins=50)
ax.set_title('first histogram')
ax.set_xlabel('x')
ax.set_ylabel('freq')
fig.show()
#ジャックベラ検定を行う。
jarque_bera_test = stats.jarque_bera(x)
print('Jack Bera:', '\t', jarque_bera_test)
(実行結果)ジャックベラ検定の結果、p-value>0.05と算出されているので標本は正規分布に従っているという帰無仮説を採択できます。
test.txt
Jack Bera: (JB=0.3352314362400006, p-value=0.8456787512712962)
###例2
自由度1のχ二乗分布に従う乱数を10000個発生させ、標本を作製します。その標本に対してジャックベラ検定を行い、標本が正規分布に従うかを検定します。
sample.py
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
#正規分布に従う乱数を発生させる。
x = np.random.normal(0, 1, 10000)
kai=x*x #kaiはχ二乗分布に従う
#標本のヒストグラムを描写する。
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
ax.hist(kai, bins=50)
ax.set_title('first histogram')
ax.set_xlabel('kai')
ax.set_ylabel('freq')
fig.show()
#ジャックベラ検定を行う。
jarque_bera_test = stats.jarque_bera(kai)
print('Jack Bera:', '\t', jarque_bera_test)
(実行結果)ジャックベラ検定の結果、p-value<0.05と算出されているので、帰無仮説は棄却され標本は正規分布には従っていないという対立仮設が採用されます。
test.txt
Jack Bera: (JB=89946.17232671285, p-value=0.0)
