この記事はStan Advent Calender 2017_12月18日の記事として作成した資料です。Krone et al. (in press) によるA multivariate statistical model for emotion dynamics の内容を紹介することで、Rstanを用いた情動ダイナミクスのモデリングについて解説させていただきます。より詳しい内容に関しては当該論文を適宜ご参照ください。
本資料の目的は、Stanを用いた情動の時系列データの解析に関する理解となります。
動作環境:Windows, R3.4.2, rstan 2.16.2
情動
情動とは何か。いろいろな議論はありますが、今回は情動を"特定のEventに対する反応(心拍などの生理反応、表情などの行動反応、「悲しい」などの主観的情動体験)を包括的に含んだもの"としましょう。詳しい議論はここでは割愛します。今回の記事ではそのうちの一つである主観的情動体験を主に想定しています
情動は重要な出来事や変化に対して注意を向け、適切に対処する機能を有すると考えられています (e.g., Scherer, 2009)。その情動が、内・外的な環境の時間的な変動の中で生じていくことは想像に難くありません。
つまり、情動を理解していくうえではその動的な情報についても注目する必要があるでしょう。

情動の話とは何の関係もないが動的情報がいかに重要かを示す参考GIF画像
かわいすぎでは?(迫真)
Emotion Dynamic Features (EFD)
Kuppens and Verduran (2015) は時系列上で展開していく主観的情動体験の特徴 (Emotion Dynamic Features: EDF) として以下の4要素を提案しました:Emotional variability, Emotional inertia, Emotional cross-lag, Emotional granularity.
それぞれの要素についてとてもシンプルに紹介します。関連する文献などについては本家の論文をご確認ください。
Emotional variability
個人の時間内に経験した情動の変動 (Variability) を示す
+個人内分散で定量化されがち
Emotional inertia
今の情動状態を次の時点まで持ち越す (慣性:Inertia) 傾向を示す
+自己回帰で定量化されがち
Emotional cross-lag
ある情動が別の情動に及ぼす影響の度合い
+Cross-lag回帰によって定量化されがち
Emotional granularity
様々な情動を区別する (粒度:Granularity) 能力
語彙と考えればわかりやすい、かも(例:やばい ⇔ 悲しい、嬉しい、つらい)
+情動得点の共分散として定量化されがち
これらに加えてAverage Emotional Intensity および状態の変動を示す Innovation variability も重要と考えられる。
Average Emotional Intensity
まんま。情動強度の平均。
Innovation variablity
特定測定時の状態から次の時点までの状態変動性を示す
+状態空間モデル (後述) における状態の変動性によって定量化
これらの6つの要素を単一のモデルで全て取り出すことのできる夢のようなモデルがあり、
それこそがVector Auto-Regressive Bayesian Dynamic Model (VAR-BDM) なのです。
Vector Auto-Regressive Bayesian Dynamic Model (VAR-BDM)
VAR-BDMとはなにか
VARはベクトル自己回帰モデル (Vector Auto-Regressive model) のことを指しています。一変量の話もしてないのにいきなり多変量の時系列データのモデルを紹介するのもどうかと思うのですが、詳しいことはこちらやこちらの資料および参考文献をご参照ください。
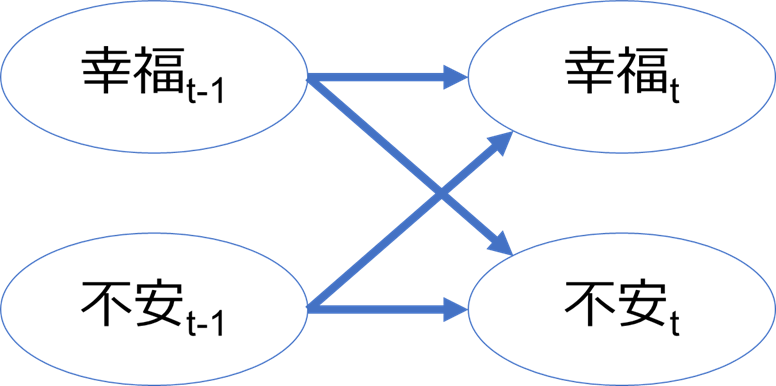
ここで簡単なVARの例を説明しておくと、二種類の情動時系列データ (幸福、不安) があるとします。ある時点tでの幸福が過去の時点 (t-1) の幸福によって予測されるとします。VARモデルでは、ある時点tでの幸福がさらに過去の時点 (t-1) の不安によっても予測されるというモデルです。不安も同様に一つ前の不安だけでなく、一つ前の幸福による影響をうけます。図にすると下図のような感じです。
このVARモデルをベイズ推定による状態空間モデル (Bayesian Dynamic Model;West & Harrison, 1997) として拡張したのがVAR-BDMです。ちなみに状態空間モデルは今年のStanアドカレの一日目から複数回紹介されているモデルです。重要なポイントは目に見えない状態の遷移を表現する状態方程式と、目に見える状態で観測誤差を含む観測方程式によってデータから誤差を分離して真の状態を推定するモデルです。図にすると下図のような感じです。
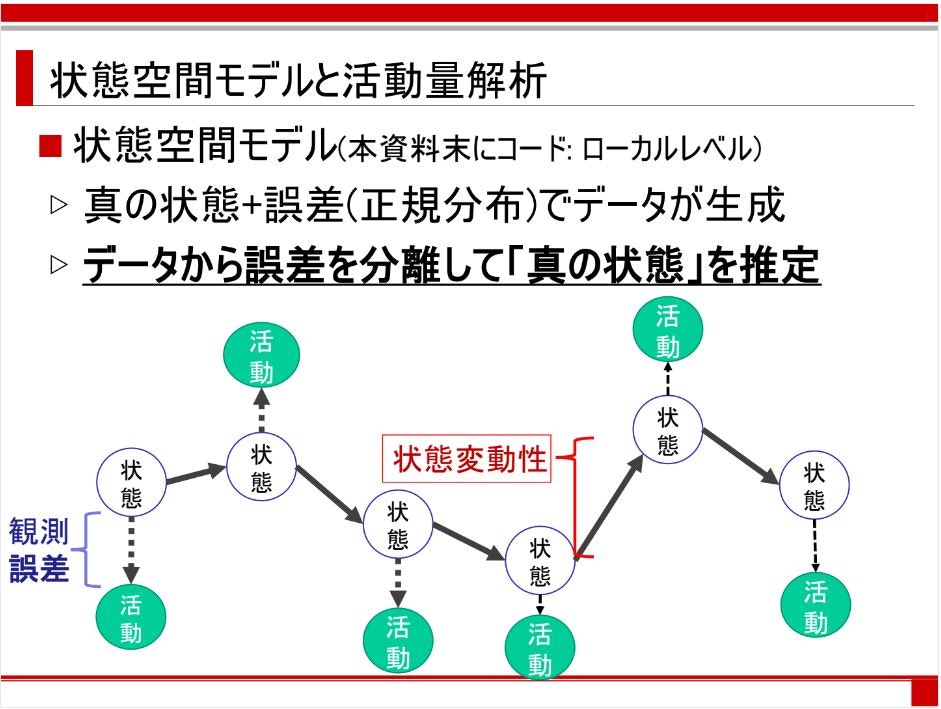
日本心理学会第81回大会シンポジウム「心理学におけるベイズ統計モデリングの可能性」での坂本さんによる発表資料p13
状態空間モデルについてはStanアドカレ内の記事はもちろん、こちらやこちら、そしてこちらの資料などが参考になります(最近はネット上の資料が本当に充実してますよね)。
今回扱うVAR-BDMは、上述の通り「観測方程式」と「状態方程式」の二つによって記述されます。
実測値 $y_{i,t}$ の「観測方程式」は以下の通りです。なお $i$ は情動の種類、$t$ は時点を意味します。
※ややこしいので個人 $n$ については記述しません。
y_t = \mu + \theta_t + \epsilon_t\qquad \qquad \epsilon_t ~ Normal(0, H) \qquad (1)
ここで, $\mu (I \times 1)$ は情動 $i$ の平均ベクトルを、$\theta (I \times 1)$ は潜在変数ベクトルを、$\epsilon_t (I \times 1)$ はホワイトノイズを、$H (I \times I)$ はホワイトノイズの共分散行列を意味しています。
さらに潜在変数 $\theta_t$ の「状態方程式」は以下の通りです。
\theta_t = \Phi \times \theta_{t-1} + \eta_t\qquad \qquad \eta_t ~ Normal(0, Q) \qquad (2)
ここで, $\Phi (I \times I)$ は自己回帰およびCross-Lag回帰行列を、$\eta_t (I \times 1)$ は状態変動誤差ベクトルを、$Q(I \times I)$ はその共分散行列を意味しています。また、$\epsilon$ と $\eta$ は相互に独立すると仮定します。
図として表現すると以下の通りになります(i = 2の場合)
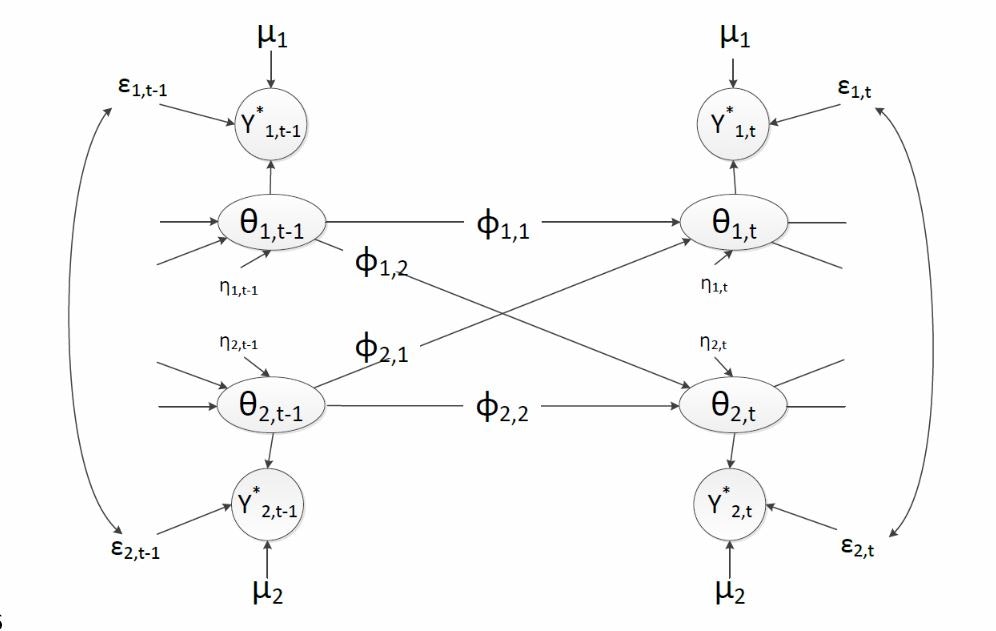
Krone et al. (in press) Figure. 1 より拝借
また、わたしの勉強不足のために十分理解していないまま記述することをここに謝罪させていただきますが、観測された分散共分散行列 $\Sigma (I \times I)$ の計算式は以下の通りです(勉強します…)。
vec(\Sigma) = (I - \Phi' ⊗ \Phi')^{-1} vec(Q+H) \qquad (3)
⊗はクロネッカー積を意味しており、これは一つの誤差項のみを持つVARモデルで用いられたリアプノフ方程式の応用らしいです (Hamilton, 1994, p.265)。ふえぇぇ。
VAR-BDM × EDF
さて、必要なパーツがそろったところで改めて先ほどまでの方程式を再掲し、EDFとして解釈する予定の各パラメータをまとめたTableを作成してみました。
y_t = \mu + \theta_t + \epsilon_t\qquad \qquad \qquad \epsilon_t ~ Normal(0, H) \quad (1)\\
\theta_t = \Phi \times \theta_{t-1} + \eta_t\qquad \qquad \quad \eta_t ~ Normal(0, Q) \quad (2)\\
vec(\Sigma) = (I - \Phi' ⊗ \Phi')^{-1} vec(Q+H) \qquad \qquad \qquad (3)
| 概念 | 定量化方法 | パラメータ |
|---|---|---|
| Emotional variability | $Y_i$の分散 | $\Sigma_{ii}$ |
| Emotional inertia | 自己回帰 | $\Phi_{ii}$ |
| Emotional cross-lag | Cross-Lag回帰 | $\Phi_{ij}$ |
| Emotional granularity | $y_i$の共分散 | $\Sigma_{ij}$ |
| Average Emotional Intensity | 平均推定得点 | $\mu_i$ |
| Innovation variability | $Y_i$のInnovation | $Q_{ii}$ |
| Krone et al. (in press) Table. 1 より一部改変 |
Stanコード
Stanコードは以下のようになります(本家で公開されているコードを適宜修正したもの)。ちなみに $\Phi$ の事前分布は時系列データ専用の無情報事前分布であり、詳しく知りたい人は Berg & Yang (1994) を参照してください。 わたしは呪文として理解しました。また、コードを見ればわかる通り原著論文によって公開されているコードにはΣを出す方法はのっておらず、方程式(3)が自分ではモデリングできなかったため、$\Sigma$ に関するパラメータが出ないことをお詫び申し上げます (後日アップデートするかも)。
data{
int<lower=2> T; //時点数
int<lower=1> I; //情動の種類
int<lower=1> N; //人数
matrix[T,I] Y [N]; //T*Iの実測値 [人数]
int M[N,T,I]; //m==1 欠損値, m==0 ならおk
int T_N[N]; //時系列の長さ
}
parameters{
matrix<lower=-1, upper=1> [I,I] phi [N]; // cross-lag 行列
corr_matrix[I] omega [N]; // H の相関行列
vector<lower=0>[I] tau [N]; // H のSDベクトル
row_vector [I] mu [N]; // 平均ベクトル
matrix[T, I] Z[N]; // 潜在得点 θ
matrix<upper=0> [I,I] X [N]; // Phiの事前分布用
vector<lower=0>[I] lambda[N]; // Q のベクトル行列
}
transformed parameters{
matrix[I,I] H[N]; // white noiseの共分散行列
matrix[I,I] Q[N]; // innovationの共分散行列
for(n in 1:N){
//quad_form_diag = SDベクトル*相関行列*SDベクトルの行列計算により共分散行列を生成する
//diag_matrix = 引数を対角項に並べた対角行列を生成する
H[n] = quad_form_diag(omega[n], tau[n]);
Q[n] = diag_matrix(lambda[n]);
}
}
model{
for(n in 1:N){
for(t in 2:T_N[n]){
// 状態方程式: 潜在得点θの推定
Z[n,t] ~ multi_normal(Z[n,t-1]*phi[n],Q[n]);
if (sum(M[n,t])==0){
// 観測方程式: y の推定
Y[n,t] ~ multi_normal(mu[n]+Z[n,t],H[n]);
}
}
}
for(n in 1:N){
mu[n] ~ normal(0,2);
tau[n] ~ cauchy(0,2.5);
omega[n] ~ lkj_corr(2);
lambda[n] ~ gamma(3,3);
for(i in 1:I){
for(j in 1:I){
//symmetrized reference prior for phi (Berger & Yang, 1994)
target += X[n,i,j] - log(1-(phi[n,j,i]*phi[n,i,j]))/2;
}
}
}
}
とりあえず手っ取り早く体験してみたい場合は、以下のサンプルデータを用いたRコードで遊んでみてください。
library(rstan)
# データ作成
data <- list()
data$N <- 1 #参加者
data$T <- 20 #Max時系列
data$I <- 2 #情動の種類
data$T_N <- array(data=20, dim=1) #個人ごとの時系列
# 欠損値配列の生成
data$M <- array(data=c(1,0,0,0,0,0,0,0,0,0,1,1,0,0,0,0,0,0,1,0,
1,0,0,0,0,0,0,0,0,0,1,1,0,0,0,0,0,0,1,0),dim=c(1,20,2))
# 観測値
data$Y <- array(data=c(1,3,2,5,3,5,5,4,3,3,1,1,2,6,6,5,5,4,1,6,1,1,1,1,1,2,3,3,2,1,1,1,5,6,3,5,2,
4,1,5),dim=c(1,20,2))
Mod <- stan_model(file="VAR_BDM.stan")
fit <- sampling(
Mod,
data=data,
iter=3000,
chains=3,
cores=3,
control=list(adapt_delta=0.90,max_treedepth=12)
#control=list()がないとサンプルデータすら収束しないことがある。
)
summary(fit)
サンプルコードを回すと以下のような結果が得られます(見やすさのため、個人の要素は抜いたものを報告してます)。
- phi[1,1][2,2] = 情動1, 2 の自己回帰:Emotional inertia
- phi[1,2][2,1] = 情動1, 2 のCross-lag回帰:Emotional cross-lag
- mu[1][2] = 情動1, 2 の平均情動強度
- Q[1,1][2,2] = 情動1, 2 の状態変動性
> print(fit, pars=c("phi","mu","Q"))
Inference for Stan model: EDF.
3 chains, each with iter=3000; warmup=1500; thin=1;
post-warmup draws per chain=1500, total post-warmup draws=4500.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
phi[1,1] 0.15 0.02 0.33 -0.50 -0.04 0.11 0.35 0.88 359 1.00
phi[1,2] 0.23 0.02 0.38 -0.63 0.01 0.23 0.48 0.92 396 1.00
phi[2,1] 0.50 0.01 0.26 -0.03 0.33 0.51 0.69 0.95 658 1.00
phi[2,2] 0.70 0.01 0.29 0.00 0.54 0.79 0.94 1.00 461 1.00
mu[1] 2.48 0.11 1.54 -0.85 1.45 2.67 3.75 4.69 180 1.02
mu[2] 0.43 0.14 1.88 -3.20 -0.94 0.46 1.97 3.62 181 1.03
Q[1,1] 0.94 0.01 0.47 0.24 0.61 0.89 1.20 2.01 1247 1.00
Q[1,2] 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 4500 NaN
Q[2,1] 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 4500 NaN
Q[2,2] 1.14 0.02 0.55 0.30 0.75 1.07 1.47 2.39 745 1.00
Samples were drawn using NUTS(diag_e) at Mon Dec 18 01:44:50 2017.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at
convergence, Rhat=1).
情動1の方が情動2よりも平均値 (mu) は大きいですが、t-1からtへの影響力は自己・Cross-lag限らず情動2の方がどちらかといえば大きいことがわかります。あと状態変動も情動2の方が大きいですが、まぁそこまで違うわけでもなさげ、ということもわかります。まぁサンプルデータが小さいのでしゃあないっすね。
今後の課題
- $\Sigma$ を出す(だれか教えてください)
- VAR-BDMを拡張する(でも今のモデルでもT=600程度の実データだと収束するのが難しかったりする)
- 離散的な状態の変化を含めたモデリングを目指す (regime-switchingなど、実はこれをアドカレの記事用にがんばっていたが間に合わなかった)
まとめ
VAR-BDMを利用して情動間のDynamicsに思いを馳せましょう!
Enjoy Stan!