この記事はStan Advent Calender 2019_12月4日の記事として作成した資料です。Rstanを用いて合計値が1になるようなデータに適用可能なモデルについて解説させていただきます。
本資料の目的は、Stanを用いたディリクレ回帰分析の適用例紹介となります。
※ディリクレ過程ではないこと、ご留意くだせぇ。
動作環境:Windows, R3.6.1, rstan 2.19.2
ディリクレ分布
ディリクレ分布。この言葉を覚えたてのときはつい口に出したくなる単語ですね。
おーい、母ちゃん!おれ今ディリクレ分布の記事書いてるぞー!
日常生活では耳にしない単語ですが、潜在ディリクレ過程とかノンパラのモデリングとかで使われることで知られています。
ですが今回は、ディリクレ分布に従いそうなデータを対象としたモデルのお話をしていきます。
確率密度関数などはWikiを参照いただければと存じます。
ディリクレ分布は『サイコロの各出る目の出やすさの分布』と言われることもありますが、
この分布が有する合計値が1になるという特徴が、本記事においては重要となります。
合計値が1になるようなデータ
例えば機械に表情を推定させるケースを考えてみましょう。
最近は画像のような形で他者の表情から感情を推定するアルゴリズムが複数存在します。

参考記事:Microsoft's Emotion Recognition Software Quantifies Feelings Based on Expressions
このようなケースであれば合計が1になる(ディリクレ分布に従うと仮定可能な)データが収集可能です。
※人間の場合でも似たような測定方法は提案可能でしょう:例
今日はこのようなデータを持っていることと仮定して、ちょっと遊んでみましょう。
どんなデータ
いくつかの表情データに対して7つの情動Ratingを機械による計算で取得したと仮定します。**あくまで仮定です。**今回は幸福[1]、怒り[2]、驚き[3]、恐れ[4]、嫌悪[5]、悲しみ[6]、中立[7]の順でRatingを書いていきます。対象とするのは恐れ表情のみとします。先行研究では、人間は恐れと驚きを混同しやすいという結果が得られてますが今回抽出したデータについてはどうでしょうか。
さらに今回対象とした表情刺激は二つの種類があるとします。一つは意図によって作成された表情 (意図表情)、もう一つは体験によって生成された表情(自然表情)です。これらの表情刺激の種類もどのように影響するのかを考えていきましょう。
RQ1:恐れ表情に対する機械が行った情動判断にどのような特徴があるのか
RQ2:その特徴が表情刺激の種類によってどのように異なるか
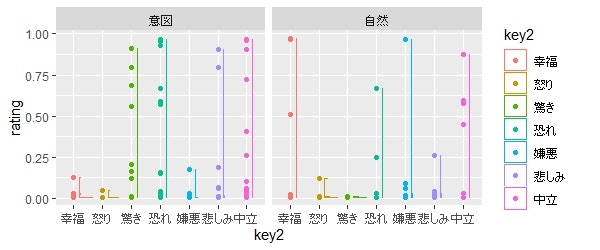
そのデータをPlotしたのが以下になります。データはまだ公開してません。ごめんね。
※なお、Dirichlet回帰に適用するために事前に合計値が1となるようないい感じの処理をDirichletRegパッケージのDR_data関数を使用しています。
library(tidyverse)
library(DirichletReg)
library(rstan)
# violin_flat用。意味なかったけど。
source("https://gist.githubusercontent.com/benmarwick/2a1bb0133ff568cbe28d/raw/fb53bd97121f7f9ce947837ef1a4c65a73bffb3f/geom_flat_violin.R")
gg_data <- gather(pl_data[,-8], key = Emo, value=rating, -Posed_Spon)
cyl_levels <- colnames(as.data.frame(data$Y[,1:7]))
gg_data$key2 <- factor(gg_data$Emo, levels=cyl_levels )
levels(gg_data$key2) <- c("幸福", "怒り", "驚き", "恐れ",
"嫌悪", "悲しみ", "中立")
labeli <- as_labeller(c(`0` = "意図",
`1` = "自然"))
p_3 <- ggplot(gg_data, aes(x = key2, y = rating, color = key2)) +
geom_flat_violin(position = position_nudge(x = .2, y = 0), alpha = .8) +
geom_point() + facet_grid(. ~ Posed_Spon, labeller = labeli)
# 出力
p_3
意図表情であれば、恐れは正しく認識可能ですが従来の研究と同じく驚きとの混合もしがちみたいですね。悲しみや中立と判断というミスもしがちです。一方、自然表情の場合は恐れよりもなんなら幸福とか嫌悪とか判断されるような自然恐れ表情刺激があるみたいですね(そしてviolin plotで浮き彫りになる深刻なデータ不足)。
もうこのPlotの確認で、この記事終わりでいいんじゃないか。という気持ちになってきましたがこの傾向がしっかり反映されているかどうか、Stanコード使ってみてみようじゃありませんか。ちなみに、今回は『中立表情』という判断をベースラインとして検討します。ソフトマックス回帰みたいなイメージでオナシャス。
Stanコード
Stanコードは以下のようになります。
data {
int<lower=1> N;
int<lower=2> ncolY; //カテゴリー数
int<lower=2> ncolX; //Predictorの数
matrix[N,ncolX] X; //説明変数の行列
matrix[N,ncolY] Y; //従属変数の行列
real sd_prior; //関連パラメータの事前分布の標準偏差。今回は5^2やってるけどいくつか試す感度分析が慣習っぽい(1~50^2)
}
parameters {
matrix[ncolY-1, ncolX] beta_raw;
real theta;
}
transformed parameters{
real exptheta = exp(theta);
matrix[ncolY, ncolX] beta;
for(l in 1:ncolX){
beta[ncolY,l] = 0.0; //基準にするための操作
}
for(k in 1:(ncolY-1)){
for(l in 1:ncolX){
beta[k,l] = beta_raw[k,l];
}
}
}
model {
theta ~ normal(0,sd_prior);
for (k in 1:(ncolY-1)){
for(l in 1:ncolX){
beta_raw[k,l] ~ normal(0,sd_prior);
}
}
for(n in 1:N){
vector[ncolY] logits;
for(m in 1:ncolY){
logits[m] = X[n,]*transpose(beta[m,]);
}
transpose(Y[n,]) ~ dirichlet(softmax(logits)*exptheta);
}
}
以下が解析+出力用Rコードです。
data <- list(N = nrow(Fear),
ncolY = 7,
ncolX = 2,
X = data.frame(Int = rep(1,nrow(Fear)), Type = Fear[,8]),
Y = DR_data(data.frame(Fear[, 1:7])),
sd_prior = 5^2)
modelD <- stan_model("Diri_reg.stan")
fitD <- sampling(modelD, data = data, iter = 10000)
# 意図
print(fitD, pars = c("beta[1,1]","beta[2,1]","beta[3,1]","beta[4,1]",
"beta[5,1]","beta[6,1]","beta[7,1]"),
digit = 2, probs = c(0.025,0.975))
plot(fitD, pars = c("beta[1,1]","beta[2,1]","beta[3,1]","beta[4,1]",
"beta[5,1]","beta[6,1]","beta[7,1]"), show_density =T)
# 自然
print(fitD, pars = c("beta[1,2]","beta[2,2]","beta[3,2]","beta[4,2]",
"beta[5,2]","beta[6,2]","beta[7,2]"),
digit = 2, probs = c(0.025,0.975))
plot(fitD, pars = c("beta[1,2]","beta[2,2]","beta[3,2]","beta[4,2]",
"beta[5,2]","beta[6,2]","beta[7,2]"), show_density =T)
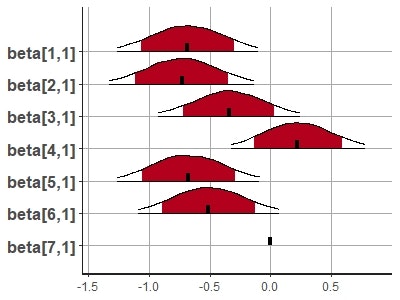
一個一個みていきましょうね。まずは意図表情。
※わかりやすさのため出力に情動単語を加えています。
> print(fitD, pars = c("beta[1,1]","beta[2,1]","beta[3,1]","beta[4,1]",
+ "beta[5,1]","beta[6,1]","beta[7,1]"),
+ digit = 2, probs = c(0.025,0.975))
Inference for Stan model: Dreg.
4 chains, each with iter=10000; warmup=5000; thin=1;
post-warmup draws per chain=5000, total post-warmup draws=20000.
mean se_mean sd 2.5% 97.5% n_eff Rhat
beta[1,1] -0.68 0 0.30 -1.26 -0.10 9785 1 <-幸福
beta[2,1] -0.73 0 0.30 -1.32 -0.14 11153 1 <-怒り
beta[3,1] -0.34 0 0.29 -0.92 0.24 11392 1 <-驚き
beta[4,1] 0.22 0 0.28 -0.33 0.78 10315 1 <-恐れ
beta[5,1] -0.68 0 0.30 -1.26 -0.09 11099 1 <-嫌悪
beta[6,1] -0.51 0 0.30 -1.09 0.07 10660 1 <-悲しみ
beta[7,1] 0.00 NaN 0.00 0.00 0.00 NaN NaN <-中立
Samples were drawn using NUTS(diag_e) at Wed Dec 04 09:54:33 2019.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at
convergence, Rhat=1).
> plot(fitD, pars = c("beta[1,1]","beta[2,1]","beta[3,1]","beta[4,1]",
+ "beta[5,1]","beta[6,1]","beta[7,1]"), show_density =T)
ベースラインを中立にしたために、恐れとは差を検出することはできませんが、それ以外の情動は大体ベースの0よりも左側に事後分布が付置していますね。驚きが健闘してますが、まだまだですね。次は自然表情です。
> print(fitD, pars = c("beta[1,2]","beta[2,2]","beta[3,2]","beta[4,2]",
+ "beta[5,2]","beta[6,2]","beta[7,2]"),
+ digit = 2, probs = c(0.025,0.975))
Inference for Stan model: Dreg.
4 chains, each with iter=10000; warmup=5000; thin=1;
post-warmup draws per chain=5000, total post-warmup draws=20000.
mean se_mean sd 2.5% 97.5% n_eff Rhat
beta[1,2] 0.56 0.01 0.56 -0.53 1.66 10371 1 <-幸福
beta[2,2] 0.08 0.01 0.56 -1.02 1.18 11549 1 <-怒り
beta[3,2] -0.38 0.01 0.56 -1.47 0.72 11507 1 <-驚き
beta[4,2] -0.50 0.01 0.55 -1.59 0.57 11150 1 <-恐れ
beta[5,2] 0.28 0.01 0.56 -0.82 1.36 11420 1 <-嫌悪
beta[6,2] 0.01 0.01 0.56 -1.09 1.11 11257 1 <-悲しみ
beta[7,2] 0.00 NaN 0.00 0.00 0.00 NaN NaN <-中立
Samples were drawn using NUTS(diag_e) at Wed Dec 04 09:54:33 2019.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at
convergence, Rhat=1).
> plot(fitD, pars = c("beta[1,2]","beta[2,2]","beta[3,2]","beta[4,2]",
+ "beta[5,2]","beta[6,2]","beta[7,2]"), show_density =T)
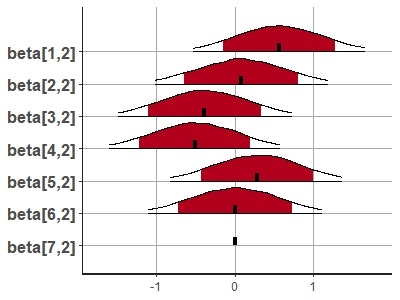
上記のデータに関するPlot見ればわかるんですが、幸福と嫌悪は100%と判断された外れ値に事後分布がかなり引っ張られてますね。それと同時に広がりが大きいのもわかると思います。もっとデータが必要なのでしょう。自然恐れ表情はもう恐れ表情を名乗るのはやめましょう、と機械がいっています(暴論)。
まとめ
RQ1:恐れ表情に対する機械が行った情動判断にどのような特徴があるのか
⇒中立と判断されがち。
RQ2:その特徴が表情刺激の種類によってどのように異なるか
⇒意図表情ならまだしも、自然表情は恐れ表情としてクソ。
Plot見ればわかることでしたが、それをDirichlet回帰分析を適用することで、推測統計の観点から色々と情報を取り出すことができました。ん?できたか?
まぁそんなことはええねん。とにかく、
Enjoy Stan!