LoginSignup
4
4

More than 5 years have passed since last update.

StanAdvent Calendar 2018Day 24
@NSushi

Bridge samplingでモデル比較実践：多項過程ツリーモデル

Last updated at Posted at 2018-12-23

どうも。この記事はStan Advent Calendar 2018の12月24日（クリスマスイブ）の記事として作成した資料です。あなたは今どこで何をしていますか？この空の続く場所にいますか？私は英国でのクリスマスイブを一人で過ごして暇を持て余しています。

ベイズ統計をはじめたての人が抱く悩みって「ええっ❣️😳💦もうすぐクリスマス🎄🎅なのにBayes Factor💏💑💕出せないってマジ❕❓😱💦💦😢⤵️このままだと平成最後👺❗のクリスマス🤶🎄もまた😦モデル比較できず😢💔😖⤵️そんなのヤダヤダぁ〜〜😭💔💦実は🙊💭Rパッケージに🌝✨Stan使ってBayes Factor😘👦💕計算できるのがあるみたいなんだけどDMでやり方💐💌💖教えてくれたら一発KO👊💥するのになぁ😳」ではないでしょうか。

そんな悩みにお答えするべく、今回はRstanとBridgesamplingと呼ばれるパッケージを使ってBayes Factorを算出してみましょう。Stanじゃなくていいよぉ、という人はBayes Factorパッケージでも簡単に計算できるのでそちらもよければどうぞ。ただしそのパッケージよりも複数の事前分布で感度を検討できるJASPやbrmsの方がいいだろう、ていうかもうStanで直に君の検討するモデルを書くのだ:muscle::muscle:というのが平成最後の私による個人的な感想です。まぁぼくはbrmsでいいです。

※brmsでBFを計算する実践例は同じくStanアドカレ16日目の紀の定さんによるbrms入門記事にて紹介されてるのでそちらもぜひ。

この記事の目的

  • 二つの仮想データを用いた実践例 (分布のあてはめ、多項過程ツリーモデル) を通して、Bridgesamplingパッケージを用いたモデル比較の仕方を知る

Bayes Factorってなに？

　Stan Advent Calendar 2017の21日目を担当した北條さんの記事にあるんでそれ見てください。そしてその資料の中に今回扱うパッケージ (Bridgesampling) の紹介も含めたBFの解説スライドがあるので、それを見てください。説明は以上です。

といいたいところですが、BFがメインの記事でそれで終わるのはさすがにアレなのでいくつか簡単な説明をします。

  1. Bayes Factor は二つのモデルに対してどちらをデータが支持するかの程度を数量化したもの
  2. Bayes Factor は比較対象となるモデル以外については語りえない＝モデル選択は慎重に
  3. 発展途上の技術なので「どんな複雑なモデルにも適用可能」と思わない

実践例1：満足度

ここでは、1000人の顧客にある商品に対する満足度を0-100％で回答させる課題を考えます。とある商品に対する満足度の平均は36.95, SDは43.28でした。これらの結果から、「まぁ1000人もいれば正規分布にそこそこ近似するだろう」と考え、このとある商品に対する満足度を要約すると「大体36.95％周辺で回答する人が多く、満足度の回答にはそこそこの散らばりがあるようだ。」という解釈をしてもよいでしょうか。

データ分析において重要なのは、視覚化です(私見です)。いったん、この満足度がどういった性質を持っていそうか確認するために、図示してみましょう。
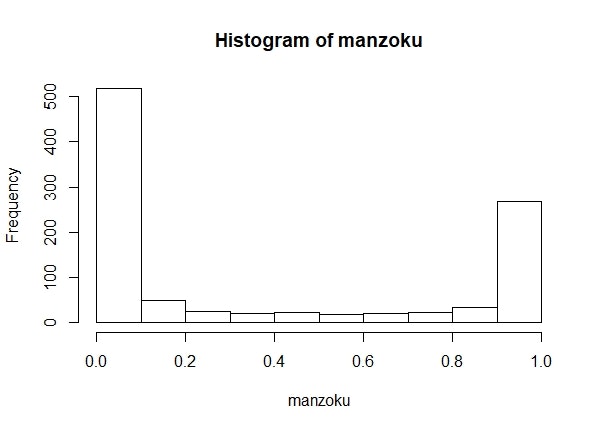
manzoku.jpeg

ふぁっ！？36％周辺で回答しとるやつなんてぜんぜんおらんやんけ！

まぁそういう風にデータを生成したから当たり前なんですけどね。むしろ、今回の満足度データは連続量でありながら、コインの裏表のように「めちゃくちゃドはまりする人と死ぬほどドはまりしない人」の二種類に分けるようなデータであるようですね。相当トガった商品のようです。
ほんとにそうでしょうか？いやまぁ「ヒストグラム見たら明らかだろ」というのはまぁその通りなんですがそんないけずなこと言わずに、ここはBayes Factorを用いたモデル比較で白黒はっきりさせましょうよ。コインの裏表を規定するような連続型の確率分布といえば、ベータ分布ですね。二項分布の事前分布としてお世話になった方も多いかと思います。

今回はこのデータを要約する推測統計量として、正規分布の μ (σ) がふさわしいのかベータ分布の α (β) が望ましいのかをBayes Factorを用いたモデル比較で明らかにしていきましょう。

モデルの書き方

まずは満足度の生成メカニズムに正規分布をあてはめるStanコードですね。ただ正規分布をあてはめるだけなのでモデルはシンプルです。今回はσの事前分布に尺度パラメータが2.5の半コーシー分布を仮定します。Bridgesamplingパッケージではmodelの書き方が通常の場合と異なり、target記法で記述する必要があります。

例えば y ~ normal(0,1)はtarget += normal_lpdf(y|0,1)というような書き方になります。連続型であればlpdf, 離散型であればlpmfです。コメントアウトした部分に通常の書き方を載せておきます。

norm.stan
data {
  int<lower=0> N;
  vector<lower=0,upper=1>[N] rating;
}
parameters { 
  real mu;
  real<lower=0> sigma;
}
model {
  target += cauchy_lpdf(sigma|0, 2.5)
    - 1 * cauchy_lccdf(0 | 0, 2.5);  // sigma ~ cauchy(0,2.5)
  target += normal_lpdf(rating|mu,sigma); // rating ~ normal(mu,sigma)
}

このコードにはワンポイント工夫がありまして、半コーシーのように負の値をとらないつもりの事前分布をtarget記法で記述する場合はcauchy_lpdf(hoge|0, 2.5)に加えて-1*cauchy_lccdf(0|0, 2.5)というのを加えてください。詳しくはこちらのFAQを参照してください。

さて、次はベータ分布をあてはめるStanコードです。ここではφとλのパラメータを用いた再パラメータ化を実装したコードを載せています。詳しくはStan reference manualの21章あたり(日本語版：翻訳者の皆様に感謝！)を参照してください。

beta.stan
data {
  int<lower=0> N;
  vector<lower=0,upper=1>[N] rating;
}
parameters { 
  real<lower=0,upper=1> phi;
  real<lower=0.1> lambda;
}
transformed parameters{
  real<lower=0> a;
  real<lower=0> b;
  a = lambda*phi;
  b = lambda*(1-phi);
}
model {
  target += pareto_lpdf(lambda|0.1,1.5); // lambda ~ pareto(0.1,1.5);
  target += beta_lpdf(rating|a,b); // rating ~ beta(a,b);
}

さて、それではMCMCしていっちゃいましょう。ちなみにこのとき、近似対数周辺尤度(Bayes Factor)の計算で用いるのでIterationの数は大きめにとっておいてください。
※ベータ分布へのあてはめを行うために、0と1のデータは事前に処理を行っています。

manzoku1.R
# データ作成
set.seed(2521)
manzoku <- rbeta(1000,0.10,0.15)
mean(manzoku)
sd(manzoku)
![Rplot01.jpeg](https://qiita-image-store.s3.amazonaws.com/0/151882/70f3711d-bbf0-4f35-f7d1-0b177c0478bf.jpeg)

hist(manzoku)

# ベータ分布で収束させるための処理
for(i in 1:1000){
  if(manzoku[i] == 1){
    manzoku[i] <- 0.9999999999
  }else if(manzoku[i] == 0){
    manzoku[i] <- 0.0000000001
  }
}

normalM <- stan_model("norm.stan")
normfit <- sampling(normalM,   
                    data=list(N = 1000, rating = manzoku), 
                    iter=50000,
                    chains=3, 
                    thin=1
)

betaM <- stan_model("beta.stan")
betafit <- sampling(betaM,   
                      data=list(N = 1000, rating = manzoku), 
                      iter=50000,
                      chains=3, 
                      thin=1
)

そんなこんなでそれぞれの推定結果を見てみましょう、まずは正規分布のモデルです！
※今回のデータではすべてRhatは1.01以下であり収束していることを確認しています。煩雑となるので報告は割愛します。

normresult.R
> print(normfit,pars=c("mu","sigma"))
Inference for Stan model: norm.
3 chains, each with iter=50000; warmup=25000; thin=1; 
post-warmup draws per chain=25000, total post-warmup draws=75000.

      mean se_mean   sd 2.5%  25%  50%  75% 97.5% n_eff Rhat
mu    0.37       0 0.01 0.34 0.36 0.37 0.38  0.40 72417    1
sigma 0.43       0 0.01 0.41 0.43 0.43 0.44  0.45 72094    1

# 予測分布とデータのあてはめ
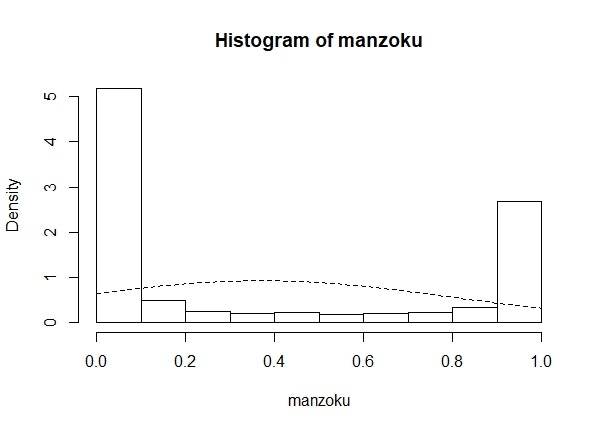
> temped <- function(z){dnorm(z,0.37,0.43)}
> hist(manzoku,freq=F)
> curve(temped,add=T,lty=2)

norm.jpeg

　...ものすごいあてはまってないですね。なんか申し訳ないですね。

betaresult.R
> print(betafit,pars=c("a","b"))
Inference for Stan model: beta.
3 chains, each with iter=50000; warmup=25000; thin=1; 
post-warmup draws per chain=25000, total post-warmup draws=75000.

  mean se_mean   sd 2.5%  25%  50%  75% 97.5% n_eff Rhat
a 0.10       0 0.00 0.09 0.10 0.10 0.10  0.10 75260    1
b 0.15       0 0.01 0.14 0.15 0.15 0.16  0.17 39374    1

> temped <- function(z){dbeta(z,0.10,0.15)}
> hist(manzoku, freq=F)
> curve(temped,add=T,lty=2)

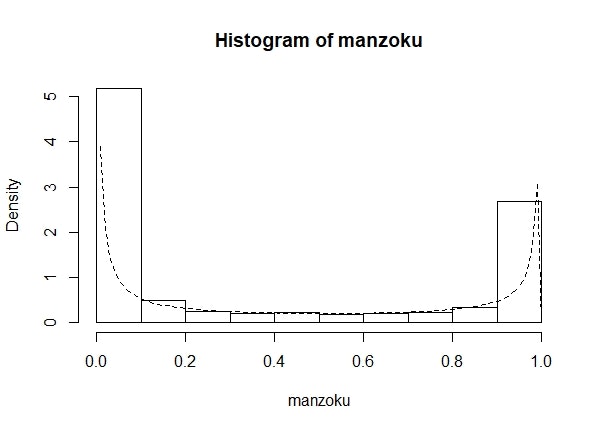
beta.jpeg
データを刈り取る形をしているだろう？かなり予測分布がデータに沿った形であることがわかりますね。というか仮想データの真値 (α ＝ 0.10, β = 0.15) と一致してますもんね。

モデル比較

さて、最後に本記事の肝であるBridgesamplingパッケージのbridge_sampler()によって近似対数周辺尤度を算出して、bf()を用いることによってBayes Factorを計算してしまってどちらのモデルがよりデータにあてはまるモデルであるのか、雌雄を決しましょうか。

BFcompare.R
> No_bridge <- bridge_sampler(normfit)
Iteration: 1
Iteration: 2
Iteration: 3
Iteration: 4
> Be_bridge <- bridge_sampler(betafit)
Iteration: 1
Iteration: 2
Iteration: 3
Iteration: 4
> print(bf(Be_bridge,No_bridge))
Estimated Bayes factor in favor of Be_bridge over No_bridge:    Inf

I...Inf!? なるほどなるほど...。正規分布モデルに対して､ベータ分布モデルを支持する程度が無限倍であることがわかります｡ ということでBayes Factorによる結果から考えても「ヒストグラム見たら明らかだろ」と言っていることが明らかになりました。ヒストグラム見たら明らかでした、すいませんでした1。

今回の結果から商品に対する満足度がθに基づく二項分布によって生成されたと考えることで(すいません、計算は省略します)、とある商品は「39％程度の確率で大満足、61％程度の確率で全然満足しない」ようなトガった商品であるといった結論がいえるでしょう。

実践例2：虚偽検出編

Bridgesamplingパッケージではなんでも、とまではいいませんがそこそこ複雑な階層モデルに対してもある程度近似した対数周辺尤度を計算することができます。

そこで次の例ではとある心理実験の仮想データを用いて、階層モデルの場合におけるBF算出の実践例を紹介します。とはいっても、Stanコードが複雑になっていても基本の計算やり方 (stan codeをtarget記法にする) はほとんど同じなのでご安心ください。

虚偽検出編で用いるデータ

この心理実験では嘘をついている人の映像と真実を話している人の映像の二種類を呈示します。目的は「二種類の映像から観察者は正しく真実を見抜くことができるのか」、を明らかにするものです。参加者は呈示された映像に対して、「真実である」「真実でない（嘘をついている）」の二種類で回答したとしましょう。

本研究ではこうした心理実験課題によって測定するデータに対して多項過程ツリーモデル:christmas_tree:を適用する実践例を紹介します。今回は一人240回回答したとする仮想データを用います。仮想データです(謎の念押し)。

多項過程ツリーモデルとは

多項過程ツリーモデルとは二値以上のカテゴリカルデータに適用するモデルであり、人の認知プロセスをモデル化するためのアプローチです。そして最近僕の中でアツいモデルになります。

今回用いる仮想データを例に具体的に考えていきましょう。今回の虚偽検出に関する研究では以下の4つの反応カテゴリーが考えられます。

  • 嘘つき映像に対して「うそやん」と回答
  • 嘘つき映像に対して「本当やん」と回答
  • 真実を言っている映像に対して「うそやん」と回答
  • 真実を言っている映像に対して「本当やん」と回答

多項過程ツリーモデルではこれらの反応カテゴリーに至るプロセスを以下のような感じで記述します。

ここでは各反応カテゴリーに至るまでのプロセスがDnあるいはDoとよばれるパラメータによってきまってますよー的なことをモデルとして記述しているわけです。
各パラメータの解釈は以下になります。

  • Dn: 嘘を正しく見抜くことができるパラメータ（高いほど虚偽映像に対して「うそやん」と回答できる）
  • Do: 真実を正しく見抜くことができるパラメータ（高いほど真実映像に対して「本当やん」と回答できる）

SDTと異なる点は信号検出力を「誤情報を誤情報と見抜く検出力」と「正しい情報を正しい情報と見抜く検出力」の二種類に分けて推定することができる点です。もちろん二つの検出力が同じパラメータであるだろう、という仮定をモデルに組み込むことも非常に簡単に導入することができます(Dn = Doとするだけ)。

Stanコードにするとなかなか単純です。上述の反応カテゴリーに至るまでのパラメータをそのまま記述しましょう。全部書くと面倒なので今回のモデルの重要な部分だけ記述しますね。

exampleMPT.stan
transformed parameters{
  simplex[2] theta_F;
  simplex[2] theta_T;
  theta_F[1] <- Dn;
  theta_F[2] <- (1 - Dn);
  theta_T[1] <- (1 - Do);
  theta_T[2] <- Do;
}
model {
  k_1 ~ multinomial(theta_F);
  k_2 ~ multinomial(theta_T);
  }
}

　このように多項過程ツリーモデルは、反応カテゴリーに至るまでのプロセスを記述し、自分にとって興味のあるパラメータを推定することができる枠組みである、ということが理解できたと思います。多分。それではさっそく簡単な拡張をしてモデル比較をしていきましょう。

多項過程ツリーモデルの拡張：推測パラメータ

先ほどのモデルはある映像を見たときに常にDnあるいはDoパラメータによって回答が規定されている、というとてもシンプルなモデルでした。しかし、我々が他者の内的状態 (今回の場合だとうそをついているかどうか) を推定する場合、「いや絶対うそやん」てときと「うーん、うそ...なんかなぁ？」といったような確信を持ってる状態と確信を持てない状態がありうる、ということは直観的に理解できると思います。図にするとこんな感じです。

推測パラメータgを加えた新しいモデルでは反応カテゴリーに至るプロセスにgを新たに加えることで以下のような感じで記述します。

ちなみにgパラメータの位置を工夫すれば「真実である」と答えやすい傾向、のような反応バイアスと対応するパラメータとして扱うこともできます。今回のgパラメータを先ほどのStanコードに加えるとこんな感じです。

exampleMPT_gparameters.stan
    theta_F[1] = Dn + (1-Dn)* g; 
    theta_F[2] = (1-Dn)*(1-g);
    theta_T[1] = (1-Do)*(1-g); 
    theta_T[2] =  Do+(1-Do)*g;

さて、それではこの推測パラメータを入れた場合のモデルを推測モデル、そうでないモデルを非推測モデルと名付けましょう (名前は適当です)。この二つのうちどちらがよりデータを支持するモデルであるのかを、をBayes Factorを用いることによって決めちゃいましょう。

モデルの書き方

本記事では、単純な多項過程ツリーモデルを比較するのではつまらないので各パラメータには個人差が含まれているであろう、という仮定を含めた階層モデルを用います。Bayes Factorによる階層性を持った多項過程ツリーモデルの比較はGronau et al., 2018でも実践例が紹介されているのでよろしければそちらもぜひ。

多項過程ツリーモデルに階層性を持たせる場合には大きく、ベータ分布を用いる場合と多変量正規分布を用いる場合の二種類があると著者は理解しています。今回はパラメータ間の相関を仮定することのできる後者のモデル(潜在特性多項過程ツリーモデルとも呼ばれます)を適用しましょう。今回はBayesian Cognitive ModelingのCase studyにおけるコードを参考にして作成しています2。

最初のモデル (非推測モデル) を記述したStanコードは以下の通りです。

model1.stan
data { 
  int<lower=1> N; //参加者の数
  int<lower=0,upper=160> k_1[N,2]; //偽物に対する判断
  int<lower=0,upper=160> k_2[N,2]; //本物に対する判断
}
parameters {
  matrix[2,N] deltahat_tilde; //parameter間の相関に必要

  cholesky_factor_corr[2] L_Omega; //〃
  vector<lower=0>[2] sigma; //〃
  real muDnhat; //偽物を見抜けるぞ平均パラメータ
  real muDohat; //本物を見抜くぞ平均パラメータ
} 
transformed parameters {
  simplex[2] theta_1[N]; //個人の偽物判断時の能力
  simplex[2] theta_2[N]; //個人の本物判断時の能力
  vector<lower=0,upper=1>[N] Dn; //個人の偽物を見抜けるぞパラメータ
  vector<lower=0,upper=1>[N] Do; //個人の本物を見抜くぞパラメータ

  matrix[N,2] deltahat = (diag_pre_multiply(sigma, L_Omega) * deltahat_tilde)'; //呪文
  vector[N] deltaDnhat; //偽物略の個人差
  vector[N] deltaDohat; //本物略の個人差

  for (i in 1:N) {

    deltaDnhat[i] = deltahat[i,1];
    deltaDohat[i] = deltahat[i,2];

    // みんな大好きプロビット変換 
    Dn[i] = Phi(muDnhat + deltaDnhat[i]);
    Do[i] = Phi(muDohat + deltaDohat[i]);

    // 刺激と判断の組み合わせに用いられるパラメータの式
    theta_1[i,1] = Dn[i]; //偽物に対して「偽物！」といえる場合
    theta_1[i,2] = 1-Dn[i]; //偽物に対して「本物！」といっちゃった場合
    theta_2[i,1] = 1-Do[i]; //本物に対して「偽物！」といっちゃった場合
    theta_2[i,2] = Do[i]; //本物に対して「本物」といえる場合
  }
}
model {
  // Priors
  target += normal_lpdf(muDnhat| 0, 1); //muDnhat ~ normal(0,1);
  target += normal_lpdf(muDohat| 0, 1); //muDohat ~ normal(0,1);

  target += lkj_corr_cholesky_lpdf(L_Omega|4); //L_Omega ~ lkj_corr_cholesky(4);
  target += cauchy_lpdf(sigma|0, 2.5)
    - 1 * cauchy_lccdf(0 | 0, 2.5);  //sigma ~ cauchy(0,2.5);
  target += normal_lpdf(to_vector(deltahat_tilde)|0, 1); //to_vector(deltahat_tilde) ~ normal(0,1);
  // Data
  for (i in 1:N){
    target += multinomial_lpmf(k_1[i]|theta_1[i]); //k_1[i] ~ multinomial(theta_1[i]);
    target += multinomial_lpmf(k_2[i]|theta_2[i]); //k_2[i] ~ multinomial(theta_2[i]);
  }
}
generated quantities {
  real<lower=0,upper=1> muDn;
  real<lower=0,upper=1> muDo;
  corr_matrix[2] Omega;
  // 平均、相関算出用の事後変換
  muDn = Phi(muDnhat);
  muDo = Phi(muDohat);

  Omega = L_Omega * L_Omega';
}

もう一つの推測パラメータを含めた推測モデルのStanコードは以下の通りです。上のコードからわかる通り、今回用いるStanコードはアホほど長いので重複しそうなところは基本的に省略してます。

model2.stan

...
parameters {
... //※Dn,Do,g(=3)の数だけ相関行列に関係するパラメータも増やしておく
  real muDohat;
  real mughat; //推測パラメータ用
} 
transformed parameters {
...
  vector<lower=0,upper=1>[N] Do;
  vector<lower=0,upper=1>[N] g; //推測パラメータ(New

...
  vector[N] deltaDohat;
  vector[N] deltaghat; //推測パラメータ(New

  for (i in 1:N) {
    ...
    deltaDohat[i] = deltahat[i,2];
    deltaghat[i] = deltahat[i,3]; //推測パラメータ(New

    ...
    Do[i] = Phi(muDohat + deltaDohat[i]);
    g[i] = Phi(mughat + deltaghat[i]); //推測パラメータ(New

    // 刺激と判断の組み合わせに用いられるパラメータの式
    theta_1[i,1] = Dn[i] + (1-Dn[i])* g[i]; //偽物に対して「偽物！」といえる場合
    theta_1[i,2] = (1-Dn[i])*(1-g[i]); //偽物に対して「本物！」といっちゃった場合
    theta_2[i,1] = (1-Do[i])*(1-g[i]); //本物に対して「偽物！」といっちゃった場合
    theta_2[i,2] =  Do[i]+(1-Do[i])*g[i]; //本物に対して「本物」といえる場合
  }
}
model {
  ...
  target += normal_lpdf(mughat| 0, 1); //推測パラメータ(New
  ...
}
generated quantities {
...
  real<lower=0,upper=1> mug; //推測パラメータ(New
...
  mug = Phi(mughat);
...
}

さてさて、それでは早速MCMCして結果をみていっちゃいましょう。まずはDn, Do パラメータのみのシンプルな非推測モデルからです！

MPTresult1

> H1Model <- stan_model("model1.stan")
> samples_1 <- sampling(H1Model,   
                       data=list(N = nrow(SD), k_1 = SD[,6:7],k_2=SD[,8:9]), 
                       iter=150000,
                       chains=3, 
                       pars= c("muDn", "muDo", "sigma", "Omega", "L_Omega", "muDnhat", 
                       "muDohat", "deltahat_tilde", "lp__"),thin=1,
                       control = list(adapt_delta = 0.99,max_treedepth=15)
 )
> print(samples_1,pars= c("muDn", "muDo", "Omega", "lp__"))
Inference for Stan model: model1.
3 chains, each with iter=150000; warmup=75000; thin=1; 
post-warmup draws per chain=75000, total post-warmup draws=225000.

                mean se_mean    sd    2.5%     25%     50%     75%   97.5%  n_eff Rhat
muDn            0.56    0.00  0.03    0.50    0.54    0.56    0.59    0.63  12739    1
muDo            0.74    0.00  0.03    0.68    0.72    0.74    0.77    0.80  13379    1

Omega[1,1]      1.00     NaN  0.00    1.00    1.00    1.00    1.00    1.00    NaN  NaN
Omega[1,2]      0.07    0.00  0.13   -0.19   -0.01    0.07    0.16    0.33  16538    1
Omega[2,1]      0.07    0.00  0.13   -0.19   -0.01    0.07    0.16    0.33  16538    1
Omega[2,2]      1.00    0.00  0.00    1.00    1.00    1.00    1.00    1.00 221024    1
lp__         -485.13    0.06 11.09 -507.95 -492.38 -484.76 -477.46 -464.48  31578    1

今回のデータだと、真実を見抜くパラメータの方が嘘を見抜くパラメータよりも少しだけ高そうですね。また、この二つのパラメータ同士の相関は低いみたいです。へー。

さて、お次は推測パラメータを新たに含んでいる推測モデルの結果を見てみましょう。

MPTresult2

> H2Model <- stan_model("model2.stan")
> samples_2 <- sampling(H2Model,   
                      data=list(N = nrow(SD), k_1 = SD[,6:7],k_2=SD[,8:9]), 
                      iter=150000,
                      chains=3, 
                      pars= c("muDn", "muDo", "mug", "sigma", "Omega", "L_Omega", "muDnhat", 
                      "muDohat", "mughat", "deltahat_tilde", "lp__"),
                      thin=1, control = list(adapt_delta = 0.99)
)
> print(samples_2,pars= c("muDn", "muDo", "mug", "Omega", "lp__"))
Inference for Stan model: model2.
3 chains, each with iter=150000; warmup=75000; thin=1; 
post-warmup draws per chain=75000, total post-warmup draws=225000.

                mean se_mean    sd    2.5%     25%     50%     75%   97.5%  n_eff Rhat
muDn            0.27    0.00  0.10    0.08    0.19    0.26    0.33    0.47  27490    1
muDo            0.51    0.00  0.10    0.29    0.44    0.52    0.59    0.70  26053    1
mug             0.31    0.00  0.09    0.11    0.25    0.32    0.37    0.46  29463    1
Omega[1,1]      1.00     NaN  0.00    1.00    1.00    1.00    1.00    1.00    NaN  NaN
Omega[1,2]      0.11    0.00  0.22   -0.42   -0.01    0.13    0.26    0.45  13039    1
Omega[1,3]      0.00    0.00  0.28   -0.49   -0.21   -0.01    0.19    0.56  22944    1
Omega[2,1]      0.11    0.00  0.22   -0.42   -0.01    0.13    0.26    0.45  13039    1
Omega[2,2]      1.00    0.00  0.00    1.00    1.00    1.00    1.00    1.00 223209    1
Omega[2,3]     -0.52    0.00  0.25   -0.88   -0.72   -0.56   -0.36    0.03  15601    1
Omega[3,1]      0.00    0.00  0.28   -0.49   -0.21   -0.01    0.19    0.56  22944    1
Omega[3,2]     -0.52    0.00  0.25   -0.88   -0.72   -0.56   -0.36    0.03  15601    1
Omega[3,3]      1.00    0.00  0.00    1.00    1.00    1.00    1.00    1.00   1219    1
lp__         -570.04    0.05 12.33 -595.22 -578.13 -569.71 -561.55 -546.87  54087    1

一つ目のモデルと同様、真実を見抜くパラメータの方が嘘を見抜くパラメータよりも少しだけ高そうですが、両方の値ともに推測パラメータの影響で小さくはなっていますね。さらに、嘘を見抜くパラメータと推測パラメータの間に相関はありませんが、真実を見抜くパラメータに関しては「真実を見抜けるパラメータが高い (低い) ほど、推測で正答に至るパラメータが低く (高く) なる」といった関係性が若干ありそうなこともわかりました。

なんだか、二つ目のモデルのほうがいろいろとリッチな情報を提供してそうですね。

モデル比較

それではどちらのモデルがデータをより支持するモデルであるのか、早速bridge_sampler()で見ていっちゃいましょう。ちなみに今回のような潜在特性MPTモデルのような複雑な階層モデルの場合にはデフォルトの引数ではなくWARP-Ⅲアルゴリズムと呼ばれるメソッドを用いましょう。使い方は簡単、bridge_sampler()の引数にmethod="warp3"と加えるだけ。

また、今回の仮想データは、デフォルトのIteration数では近似対数周辺尤度の計算が収束しません。そこでmaxiterにも10000くらいぶち込みましょう。また、MCMC(*´Д')ﾊｧﾊｧがやかましければsilent = Tをぶちこみましょう。あと計算結果の安定性を見るためにrepetitions = 3で計算を3回くらい行っておきましょう。repetitionsをいれることで推定の範囲も出してくれます。それでは最初の例と同じようにbf()によるBayes Factorの結果まで見てみましょう！

MPTmodelCompare.R
> H1_bridge <- bridge_sampler(samples_1, method="warp3",maxiter = 10000, silent = T,repetitions = 3)
> H2_bridge <- bridge_sampler(samples_2, method="warp3",maxiter = 10000,silent = T,repetitions = 3)```
> BF21 <- bf(H2_bridge, H1_bridge)
> print(BF21)
Estimated Bayes factor (based on medians of log marginal likelihood estimates)
 in favor of H2_bridge over H1_bridge: 2.39623
Range of estimates: 0.30655 to 4.20883
Interquartile range: 1.95114

ふむふむ。なるほど。Bayes Factorから、非推測モデルと比較してデータが推測モデルを支持する程度は大体2.396倍程度で、推定の範囲は0.307～4.209で、まぁそんな明確な差があるというわけではない、というか...こう、いっちゃえば微妙な感じですよね←

一応Bayes Factorに基づけば、今回用いたデータについては「推測パラメータはまぁあってもなくてもいいんじゃね？」という結論といえるでしょう。

さいごに

今回はBridgesamplingパッケージによるモデル比較について紹介させていただきました。基本的にモデル内のパラメータをtarget記法にして書けばあとはbridge_sampler()ががんばってくれる、ということを理解してもらえれば結構です。

さて、後半のモデル比較についてですが、本研究では推測パラメータがある場合とない場合でBayes Factorに大きな違いは見られませんでした。
その理由としては、今回用いられた推測パラメータ自身に推測に関わる情報が直接的に含まれていないことが一つの原因としてあげられるでしょう。それを解決するためにはあらかじめ回答とともに確信度についても測定しておくことで、「うそやん(確信度高)」「うそやん(確信度低)」といったように反応カテゴリーを拡充し、推測パラメータに必要な情報を付け足してあげるとより精度の高いパラメータが推定できると思います。
　
また、「推定結果が重すぎるし時間がかかりすぎて心が死んだ」という理由から今回はWAICを計算していません。しかしBayes Factorはモデル比較の一つの指標に過ぎず、様々な観点から評価していくことも必要と考えられるでしょう。ベイズファクターとWAICについては清水先生の神資料が有用です。予測分布も含めたほかの情報も用いて、多角的な観点からモデルの評価をしていく必要も今後あると考えられます。

本記事の多項過程ツリーモデルでは、推測パラメータの有無でモデルの比較を行っていますが、ほかにも様々な応用例が考えられます。例えば、Gronau et al., 2018ではモデル内のパラメータ同士の相関がある場合とない場合とで比較を行っています。ほかにも、特定の実験操作を虚偽・真実検出パラメータの共変量として組み込んだり、パーソナリティなどの個人特性を推測パラメータの共変量として組み込む、などさまざまな拡張の可能性が考えられるでしょう。

多項過程ツリーモデルとBayes Factorを用いてあなたもあなた好みのクリスマスツリー:christmas_tree::christmas_tree::christmas_tree:を作ってみるのなんていかがでしょうか。

Enjoy Stan!
:sparkles::sparkles:Merry Christmas!!:sparkles::sparkles:

  1. もうちょっとノイズはいった仮想データ作ればよかったですね。フヒヒ、すいません。 ↩

  2. 可読性を考えれば多変量正規分布によるコードで記述するべきでしたが、Iterationsがたくさん必要な今回の場合だとあまりにも遅いので今回はこういう書き方にしてます。ごめんちい。 ↩

4
4
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
4
4