この記事はStan Advent Calender 2019 12月13日の記事として作成した資料です。Rstanによる隠れマルコフモデルについて解説させていただきます。
本資料の目的は、美少女ゲームの紹介となります。
動作環境:Windows, R3.6.1, rstan 2.19.2
※注意:美少女ゲームの話をします。苦手な方はブラウザバックを強く推奨します。
蒼の彼方のフォーリズムについて
著者はもちろんやったことないのだけれども、spriteが制作した蒼の彼方のフォーリズム(愛称:あおかな)というゲームがある。
これは4人のヒロインと一緒に空で追いかけっこしたり背中をタッチするような架空のスポーツ、フライング・サーカス(FC)に興じる青春ものである。画像は公式ホームページより抜粋。

著者はもちろんやったことないのだけれども、このゲームのヒロインは
- ピンク:最初はFC初心者だけれども、才能が抜群なのでメキメキ成長する子
- 黒:FCの才能があるけれど、ピンクの子のずば抜けた能力についていけなくなる自分に気づいてしまう子
- 亜麻色:FC初心者だし、才能もない普通の子
- 紫:とっても頑張り屋さん。でもあんま報われない子
という個性豊かな4人である。
どのストーリーにも時には美しく、時には醜い人間の心模様が描かれておりハイパー面白い作品なのである。
余談であるが(もうずっと余談のような記事だけど)、これを当時学生の学振が全然受からないときにプレイしていたのだが、このゲームが描いているのは努力だけでは到底かなわない才能+努力する人間がブイブイいわせる世界であり、当時の私の口癖は『蒼の彼方のフォーリズムはアカデミアだ』であった。
制作した作品は数多くの人に愛され、惜しまれながらも2018年11月にあおかなを制作したspriteは解散したのだが、2019年11月28日に熱い声に応えてspriteが再結成することとなったのはもうご存知のとおりである (再結成のお知らせ)。
spriteの生み出す新たな価値に期待が高まる。
ヒロイン真白のかわいさ
著者はもちろんやったことないのだけれども、
ほかの3ヒロインに比べて実はこの亜麻色の髪の乙女は、
シリアスな場面は少なくかわいさ、イチャイチャ重視のシナリオとなっている。
それはもう気が狂うほどかわいかったのでそのかわいさをまとめた映像をYoutubeで拾った。
その後、その映像を見ているときに筆者が感じた『主観的なかわいさ』をGirard氏の開発した Continuous Affect Rating and Media Annotation, 通称CARMAによって連続的に測定した。
インターフェースは以下のような感じである。
画像は開発者HPより抜粋。
余談であるが、開発者のGirard氏は表情の研究も行っており完全に筆者の上位互換的研究者だ。
表情や統計解析に興味がある心理学者はぜひチェックしよう(→ Girard氏のHP)
最近だと「目の笑った笑顔が真の笑顔、というのは神話です」という論文を出してるぞ!僕もそう思う!
さて、そんなこんなで測定したデータは以下のような感じである。
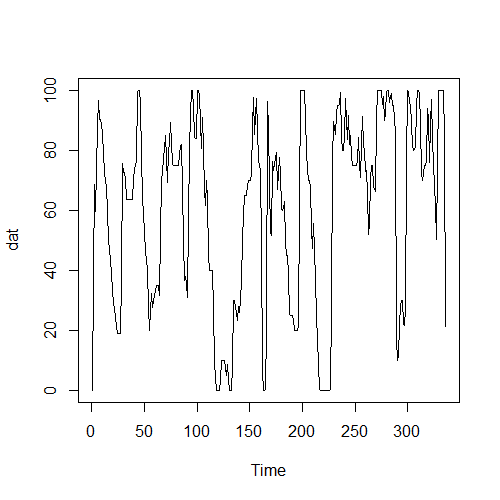
この観測されたデータの背景に『筆者が真白ちゃんをかわいいと感じている状態』と『筆者が真白ちゃんをハチャメチャにかわいいと感じている状態』の二つの隠れた状態が存在していることを仮定して、隠れマルコフモデルを適用しようと思う。
隠れマルコフモデル
隠れマルコフモデルの詳細はぐぐってもらうとして (参考資料たくさんあります)、
このモデルを適用するモチベーションには
(1) 観測値の生成にかかわるパラメータ (μ)とともにある状態から別の状態に遷移するパラメータ (Θ)を推定できる
(2) そこからの予測
があると考えられる。
ある平均μ1をもつ『筆者が真白ちゃんをかわいいと感じている状態 (Θ1)』とより高めの平均μ2をもつ『筆者が真白ちゃんをハチャメチャにかわいいと感じている状態 (Θ2)』を推定するぞー、ということになる。筆者が主観的にわかりやすいと感じている図を以下に示す。
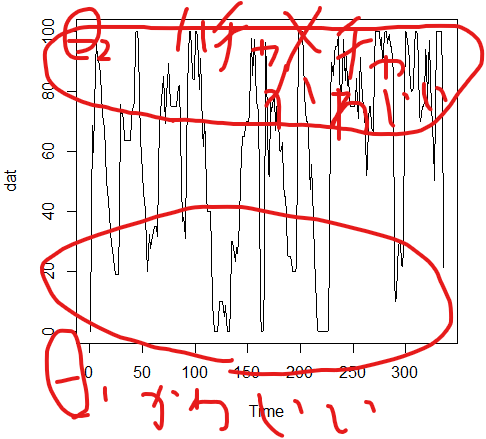
Stanコードは以下のような感じである。
最も難解そうなmodelブロックはStan reference manualに従った。
data {
int<lower=0> N; //データ数
int<lower=0> K; //状態数
real y[N]; //データ
}
parameters {
simplex[K] theta[K];
positive_ordered[K] mu;
}
model {
// 事前分布
target+= normal_lpdf(mu[1] | 0, 10); //かわいい状態の事前分布
target+= normal_lpdf(mu[2] | 80, 10); //ハチャメチャにかわいい状態の事前分布
// forward algorithm マニュアル見て(https://mc-stan.org/docs/2_18/stan-users-guide/hmms-section.html)
{
real acc[K];
real gamma[N, K];
for (k in 1:K)
gamma[1, k] = normal_lpdf(y[1] | mu[k], 1);
for (t in 2:N) {
for (k in 1:K) {
for (j in 1:K)
acc[j] = gamma[t-1, j] + log(theta[j, k]) + normal_lpdf(y[t] | mu[k], 1);
gamma[t, k] = log_sum_exp(acc);
}
}
target += log_sum_exp(gamma[N]);
}
}
結果
データをぶち込んで、推定してみマッスル。
library(rstan)
dat_y <- read.csv("hoge.csv", header=T)
stan_dat <- list(N=nrow(as.data.frame(dat_y)), K=2, y=dat_y)
fit <- stan("hiddenM.stan", data=stan_dat, iter=4000, cores=4, control=list(adapt_delta=0.99, max_treedepth=15))
print(fit, pars=c("theta","mu"), probs = c(0.05,0.95))
結果から、真白ちゃんがかわいいと感じている状態での平均値は大体22.97, ハチャメチャにかわいいと感じている状態の平均値は大体79.74であった。
真白ちゃんをかわいいと感じている状態 (Θ1) から真白ちゃんをハチャメチャにかわいいと感じている状態 (Θ2)に遷移する確率は大体9%、ハチャメチャかわいい状態 (θ2) からかわいい状態 (θ1) に戻る確率が4%ほどであった。
結論:真白はかわいいし、ハチャメチャかわいいときはハチャメチャかわいい。
今後の展望:かわいい判断データの複雑性をもっと捉えれる感じでがんばる。
閉廷!!!解散!!!!
Enjoy あおかな or stan.
