概要
論文「How anatomy shapes dynamics: a semi-analytical study of the brain at rest by a simple spin model」を元に、Ising Spinモデルでのニューロンの実装とエントロピーの計算を行います。「あるネットワークの構造そのもののエントロピー」を計算することがゴールとなります。
理解することを目的としたざっくり解説です。私自身は物理学や熱力学をしっかりやっている人間ではないので、理解不足や認識の間違いなどあれば指摘をお願いします。
ニューロンモデル
ニューロンモデルには様々な種類がありますが、「多数の入力を元に一つの出力が得られるもの」であればある種何でもいいともいえます。
この論文内ではイジングモデル(磁場のスピンの相互作用モデル)を利用し、「1」か「0」のスピン状態を持つニューロンがお互い影響を与え合うモデルを考えます。(論文に合わせて「1」と「-1」ではなく「1」と「0」の組み合わせについて見ます)
イジングモデルを扱う上で、大まかに以下のような前提があります。
-
電子はランダムに振動をしている。
- 温度が高いほど振動は激しくなり、低いほど振動は小さくなる。
-
スピンの状態に対してハミルトニアン(エネルギー)を計算することができる。
- 全体にかかる「磁場の影響」とニューロン同士の「相互作用」の二つによって計算される。
- ランダムに変化するスピンはエネルギーが低い状態に向かっていく。
ニューロンの持つエネルギー
ネットワークを隣接行列$C$という形で表し、ニューロン同士の接続の有無を1と0で表現します。接続強度は$W$とします。ネットワーク全体のある任意のスピン状態を$α$として、$i$番目のニューロンのスピン状態を$S_i^\alpha$と表現します。
この時、ニューロンの持つエネルギー(ハミルトニアン)は以下の式で計算することができます。
$$ H^\alpha = {1 \over 2 } \theta \sum_{i} S_i^\alpha - {1 \over 2 }W\sum_{ij} S_i^\alpha S_j^\alpha C_{ij}\tag{1} $$
ここで右式の第一項がイジングモデルで言うところの磁場の影響です。ニューロンとして考える場合は「ニューロンが発火することのコスト」といった形で捉えればいいでしょうか。
右式の第二項がイジングモデルでいうところの電子の相互作用です。ニューロンも電子と同様お互いに影響しあう性質があります。(マイナスの相互作用がない限り)「隣り合うニューロンは同じ状態になりたがる」ということが式として表されています。
スピン状態の変化
Glauber dynamicsによって一つのニューロンのスピン状態を変化させることを考えてみます。これは大まかにいうと、「あるスピンが反転した際のエネルギー差」からスピンが反転する確率を計算するものです。
式$(1)$において、あるニューロン$i$一個の変化が与えるエネルギー差は以下のようになります。
$$ \Delta H^\alpha = W\sum_j C_{ij}S-\theta $$
これを元に以下の式で次回のスピン状態を表す確率を計算します。
S_i =
\left\{
\begin{array}{ll}
1 & \mbox{with probability } p_i \\
0 & \mbox{with probability } 1-p_i
\end{array}\right. \tag{2}
$$ p_i=g(W\sum _ jC_{ij}S_j - \theta) \tag{3}$$
$$ g(X) = {1\over 1+e^{-\varepsilon X}} \tag{4}$$
ここで$\varepsilon$は逆温度(温度の逆数)です。数値を入れてみると温度が高いほど振動が激しくなり、低いほど振動しないことがわかります。
エントロピーの計算
$(1)$式である状態αのエネルギーを表すことができます。これを取りうる状態全てに対して計算することで、以下のように各状態を取る確率を計算することができます。
$$ P^\alpha = {e^{-\varepsilon H^\alpha}\over Z} \tag{5}$$
$$ Z = \sum _\alpha e^{-\varepsilon H^\alpha} \tag{6}$$
確率からエントロピーを求める時は$E=-\sum P\log P$として計算できます。今回は(5), (6)式を用いて式変形ができるので以下のようになります。
$$ E = -\sum_\alpha P^\alpha\log P^\alpha = {\sum_\alpha \varepsilon H^\alpha e^{-\varepsilon H^\alpha}\over Z} + \log Z $$
これで必要な式は準備できました。
実装
ここまでそろえたものをクラスとして実装します。まずコンストラクタは以下。
import numpy as np
import itertools
class IsingSpin():
def __init__(self, W, w0=1, theta=0):
self.W = W
self.w0 = w0
self.theta = theta
self.epsilon = 1
self.N = len(W)
self.reset_S()
def reset_S(self):
self.S = np.random.randint(0, 2, (self.N))
スピンを変えていく過程は以下のように実装しました。この際のアルゴリズムも様々あるのですが、シンプルにランダムなニューロンを一個ずつ選んで判定をしていく形で実装しました。
def step(self):
i = np.random.randint(0, N)
self.S[i] = self.G(self.S, i)
def sigmoid(self, x):
return 1/(1+np.exp(-self.epsilon * x))
def p(self, S, i):
s = np.dot(self.W[i], S.T)*self.w0-self.theta
return self.sigmoid(s)
def G(self, S, i):
s_p = self.p(S, i)
rand = np.random.rand()
return np.where(s_p>rand, 1, 0)
エントロピーの計算は以下のように行いました。全ての組み合わせに関してHを計算し、それを元にZやP,Eを求めます。
def E(self):
h = self.allH()
z = self.Z(h)
return sum(self.epsilon*h*np.exp(-self.epsilon * h))/z + np.log(z)
"""
これでも同じ
p = self.P()
return -sum(p * np.log(p))
"""
def H(self, S):
h1 = 1/2 * self.theta * sum(S)
h2 = 1/2 * self.w0 * sum([S[i]*S[j]* self.W[i, j] for i, j in itertools.product(range(self.N),repeat=2)])
return h1 - h2
def allS(self):
return np.array(list(itertools.product([0, 1],repeat=self.N)))
def allH(self):
return np.apply_along_axis(self.H, 1, self.allS())
def Z(self, h_array):
return np.sum(np.exp(-self.epsilon * h_array))
def P(self):
all_h = self.allH()
z = self.Z(all_h)
return np.exp(-self.epsilon * all_h)/z
動かしてみる
4×4の格子ネットワークに関して重みを変えながら動かしてみましょう。
ネットワーク生成にはnetworkxを使用します。
import networkx as nx
G = nx.grid_2d_graph(4, 4)
W = nx.to_numpy_array(G)
W_0 = np.arange(0.5, 4, 0.5)
e = []
for w_0 in tqdm(W_0):
IS = IsingSpin(W, w_0, 5)
e.append(IS.E())
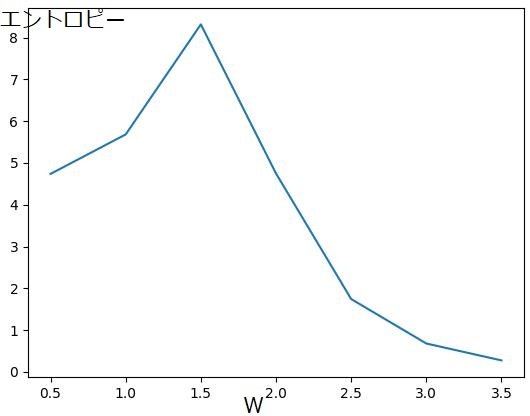
plt.plot(W_0, e)
plt.show()
設定する重みに応じてエントロピーの値が変化し、$w=1.5$でピークを迎えることがわかります。
このネットワークでは
- Wの値が低い時は「全てのスピンが0の時」が最もエネルギーが低くなる(出やすくなる)
- Wの値が高い時は「全てのスピンが1の時」が最もエネルギーが低くなる(出やすくなる)
という性質になっています。wの値を変えていったとき、w=1.5付近でそれらのちょうど中間に位置して様々な状態を取りやすくなり、複雑性が高まる、ということがわかります。
論文内ではさらにこの手法を様々なネットワークに適用し、ピークを比較して計算を行うことで、「ネットワークの構造そのものの複雑性」について調べています。
ただし計算量が$O(2^N)$で増えていくため、計算量には限界があります。普通のPCでニューロン20個までがギリギリのラインでしょうか。それ以上について比較する場合は今のような「全ての組み合わせのエネルギーを求める」形ではなくランダム性を持たせる形が必要になってきます。その際の手法については自分がよくわかっていないので今回は触れません。
参考文献
以下を参考にしました。
How anatomy shapes dynamics: a semi-analytical study of the brain at rest by a simple spin model
Rich club organization supports a diverse set of functional network configurations