まえがき
パーセプトロンの簡単な解説と、AND,OR, NAND,そして簡単な組み合わせでXORを実装する。
生物学の話をしましょう
ここは読みとばして結構です。
生体内では、神経細胞は内側と外側で成分が異なります。細胞内では$\mathrm{K}^+$イオン、外側には$\mathrm{Na}^+$イオンが多く分布しています。これは細胞膜に特定のイオンのみを通したり、汲みだしたりする機構があるためです。
この辺の機能が働いた結果、細胞の内外では電位差が生じます。ちょうどコンデンサーのように。これを静止膜電位といいます。
このコンデンサーは面白い性質を持っています。外部からイオンが流入して一定の閾値以上の入力が加わると、コンデンサーがため込んだ電荷が一気に流れ込みます。これを「ニューロンの発火」とか「スパイク」といいます。
スパイクを繰り返して細胞から細胞に電荷を伝えることで、神経伝達の電流は弱まることなく脳から末端まで情報を伝えることができるわけです。
つまり?
生物学のモデルを真似て、「一定の閾値以上の入力が加わると出力される」というモデルを考えてみましょう。
以下の式を見てください。
y = \begin{cases}
1 & (x \geq \theta)\\
0 & (x < \theta)
\end{cases}
xが閾値$\theta$を超えたらy = 1を出力する。先ほど説明した生物のモデルを極限までシンプルにしたものです。
実際の神経細胞は、イオンの受容体を増やしたり減らしたりすることで、電流の伝わりやすさを調節します。重み$w$を計算に入れてみましょう。
y = \begin{cases}
1 & (wx \geq \theta)\\
0 & (wx < \theta)
\end{cases}
また、神経細胞は一つだけでなく、たくさん繋がりあっています。xを増やしてみましょう。
y = \begin{cases}
1 & (\sum^{d}_{i = 1}w_ix_i \geq \theta)\\
0 & (\sum^{d}_{i = 1}w_ix_i < \theta)
\end{cases}
これが単純パーセプトロンです。
AND, OR, NAND回路を実装してみよう
wの値を手作業で調整して、AND回路を作ってみましょう。
入力は$x_1$と$x_2$の二つ。両方が1だと出力Yが1になる。重みとして$w_1$,$w_2$、閾値として$\theta$を設定します。
式で表すとこんな感じ。
y = \begin{cases}
1 & (w_1x_1 + w_2 x_2 \geq \theta)\\
0 & (w_1x_1 + w_2 x_2 < \theta)
\end{cases}
例えば$w_1 = 0.5, w_2 = 0.5, \theta = 0.7$で AND回路として成立します。
ではPythonで実装してみます。
def AND(X1, X2):
w1, w2, theta = 0.5, 0.5, 0.7
if w1 * X1 + w2 * X2 >= theta:
y = 1
else:
y = 0
return y
print(AND(1, 1)) # 1
print(AND(1, 0)) # 0
AND回路になりました。
さらに、これをnumpyを使って書き直してみましょう。
import numpy as np
def AND(X1, X2):
x = np.array([X1, X2])
w = np.array([0.5, 0.5])
theta = 0.7
if np.sum(w * x) - theta > 0:
y = 1
else:
y = 0
return y
結果は同じです。
$w_1,w_2, \theta$の値を調整してみましょう。以下のコードを付け足します。
def OR(X1, X2):
x = np.array([X1, X2])
w = np.array([0.5, 0.5])
theta = 0.4 # thetaを減らした。
if np.sum(w * x) - theta > 0:
y = 1
else:
y = 0
return y
def NAND(X1, X2):
x = np.array([X1, X2])
w = np.array([-0.5, -0.5])
theta = -0.7 # 全部マイナスにした。
if np.sum(w * x) - theta > 0:
y = 1
else:
y = 0
return y
print(OR(1, 0)) # 1
print(NAND(1, 1)) # 0
AND,OR,NAND回路を実装できました。
XOR回路を実装してみよう
XOR回路は同様の単純パーセプトロンでは作れません。以下、簡単に理由を説明します。
$x_1,x_2$のどちらかが1であるときだけに閾値$\theta$を超える、ということは以下の4式を同時に満たす必要があります。
w_1 + w_2 < \theta\\
w_1 \geq \theta \\
w_2 \geq \theta \\
0 < \theta
適当に変形してればこの4式が同時に成立しないことがわかります。証明おわり。
さて、じゃあ実装できないのかというとそんなことはありません。一層の回路で実現できないなら二層使えばいい。
今回はシンプルに、論理回路の簡単な組み合わせで実装します。
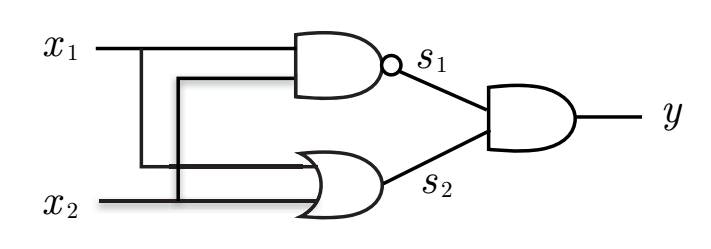
要するにこうします。
画像は『ゼロから作るDeepLearning - Pythonで学ぶディープラーニングの理論と実装』p.32より。
ANDとORとNANDを組み合わせることでXOR回路を作れます。偶然ANDとORとNAND回路が完成してますね。じゃあ実装しましょう。
def XOR(X1, X2):
return AND(NAND(X1, X2), OR(X1, X2))
print(XOR(1,0)) # 1
print(XOR(0,1)) # 1
print(XOR(1,1)) # 0
print(XOR(0,0)) # 0
できました。
まとめ
- 神経細胞の発火モデルを簡単に表したものがパーセプトロン。
- 単純パーセプトロンでは簡単な回路しか作れない。
- 何層も組み合わせることで複雑な処理を行うことができる。今回は簡単に論理回路の知識でXOR回路を作成した。
『ゼロから作るDeepLearning - Pythonで学ぶディープラーニングの理論と実装』を参考にしました。