やりたいこと
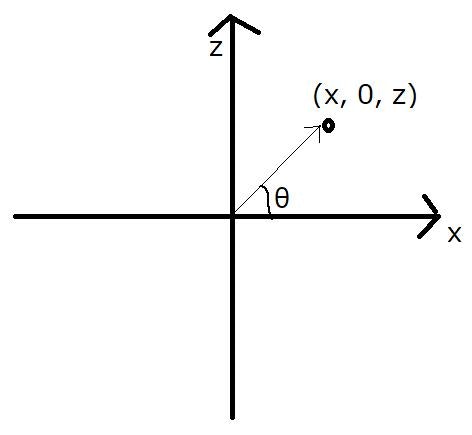
- Vector3で得られた座標を、特定の軸から見た二次元平面上の角度$\theta$として扱いたい。
(例)
以下のような$xz$座標において$x, z$の値から角度$\theta$を求めたい
結論
Mathf.Atan2(pos.z, pos.x)
のように、Mathf.Atan2関数を使う。
準備
実際に挙動を見てみる。
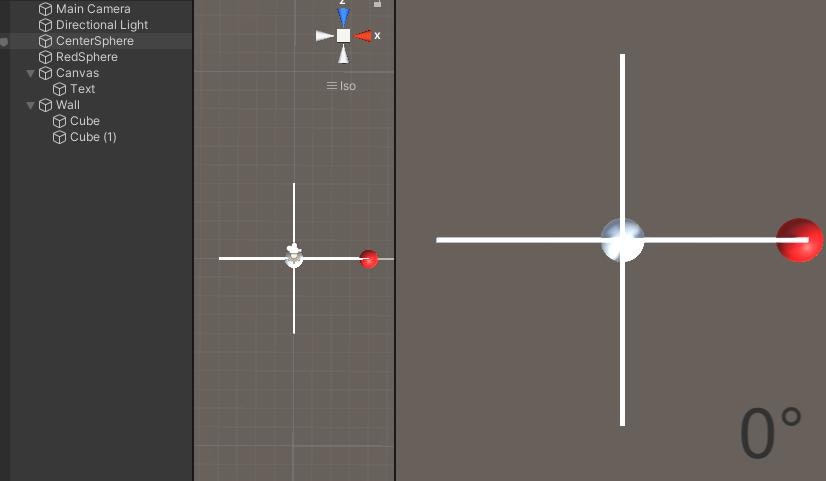
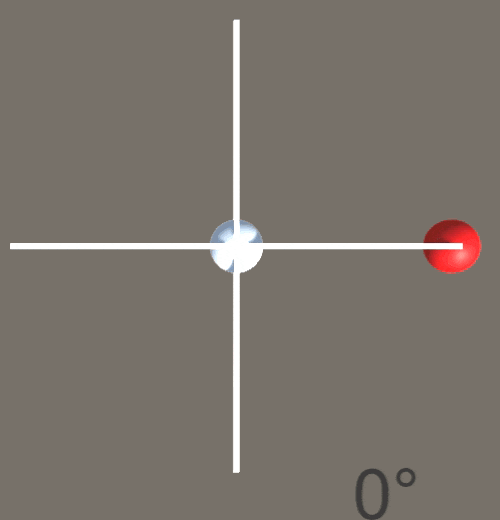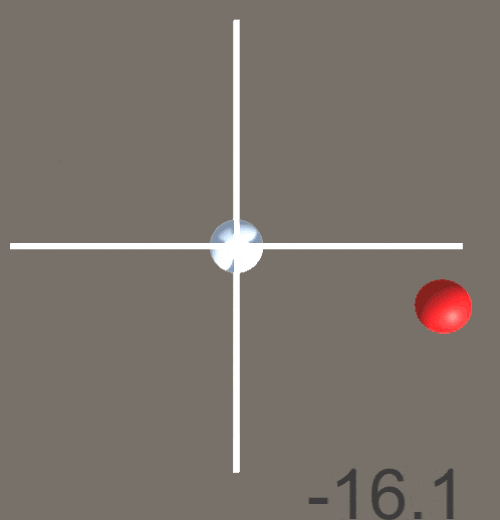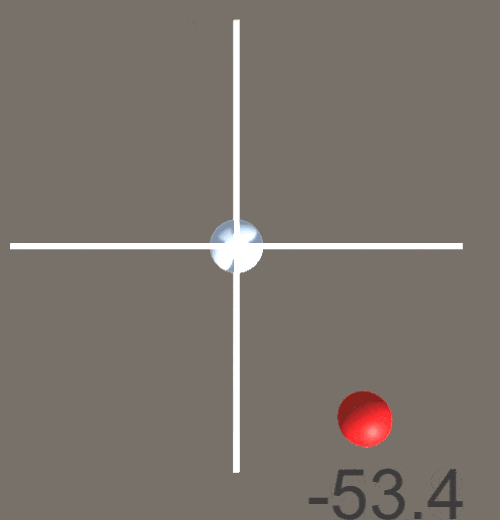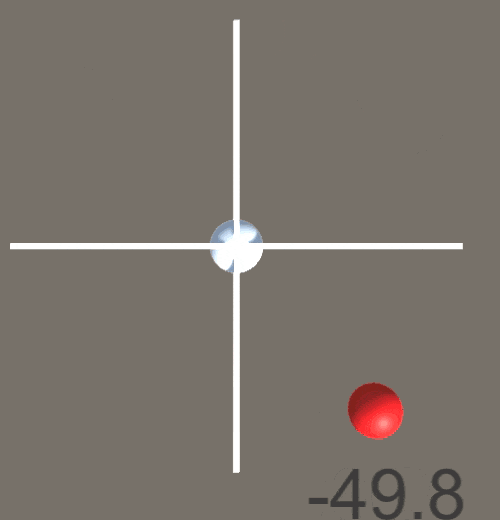
テスト用に以下のようなシーンを作成した。cubeを二つ作って簡単にxz軸表示、sphereを二つ作って中心点と目標地点とする。
また、求めた角度を表示するためのCanvas,Textを作成。
以下のようなスクリプトを割り当て、目標地点となる赤い点が円周上をぐるぐる回るようにした。
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
using UnityEngine.UI;
public class Vector2Angle : MonoBehaviour
{
public Transform obj;
public Text text;
float rot = 0f;
float r = 4f;
float speed = 0.3f;
void Update()
{
rot += speed;
obj.position = Angle2Vector(rot, r);
text.text = $"{Vector2Angle1(obj.position)}";
}
Vector3 Angle2Vector(float angle, float r)
{
return new Vector3(Mathf.Cos(angle*Mathf.Deg2Rad), 0f, Mathf.Sin(angle*Mathf.Deg2Rad)) * r;
}
float Vector2Angle1(Vector3 pos)
{
// ここに処理を書く
return 0f;
}
途中で使用した角度→ベクトルへの変換はシンプルにSinとCosを用いて以下のように実装した。これで赤い点がぐるぐる回るようになる。
Vector3 Angle2Vector(float angle, float r)
{
return new Vector3(Mathf.Cos(angle*Mathf.Deg2Rad), 0f, Mathf.Sin(angle*Mathf.Deg2Rad)) * r;
}
Atan関数を普通に使ってみる
まずは単純に$tan^{-1}$として$Atan$関数を用いて求めてみる。$x=1$地点での$z$座標、つまり$z/x$を入れればよい。
float Vector2Angle1(Vector3 pos)
{
return Mathf.Atan(pos.z/pos.x) * Mathf.Rad2Deg;
}
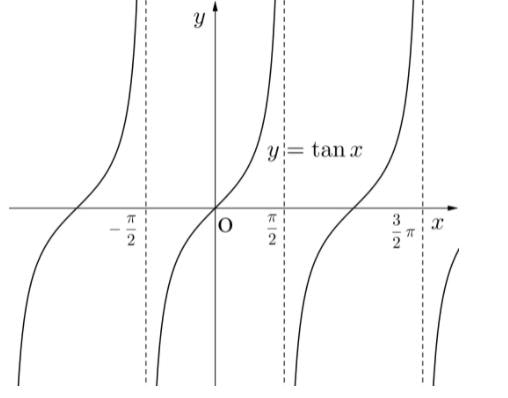
出力結果として-90°~90°の範囲しか得られない。これはtan関数が180°ごとにループする関数であるためである。
画像は高校数学.netより引用: https://xn--48s96ub7b0z5f.net/sankakukansuu-graph-2/
Atan2関数を使ってみる
この問題を解消するのがAtan2関数。これを用いて同様の計算を行ってみる。
float Vector2Angle1(Vector3 pos)
{
return Mathf.Atan2(pos.z, pos.x) * Mathf.Rad2Deg;
}
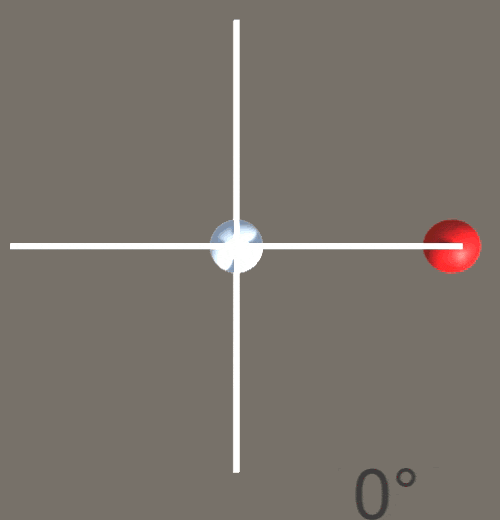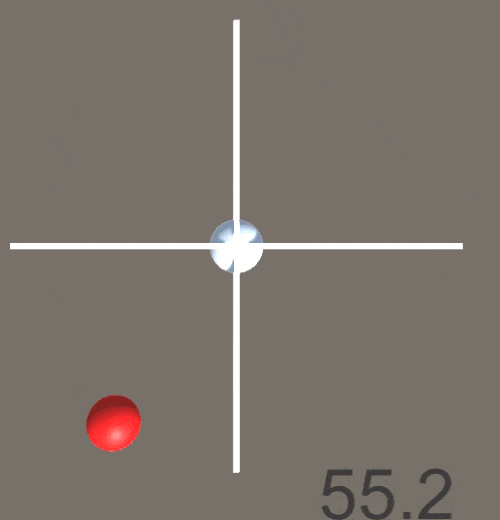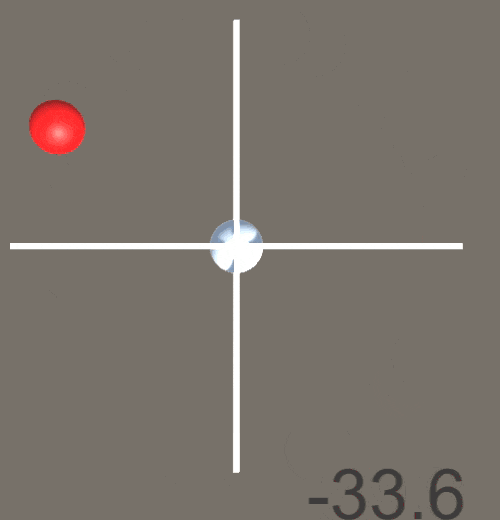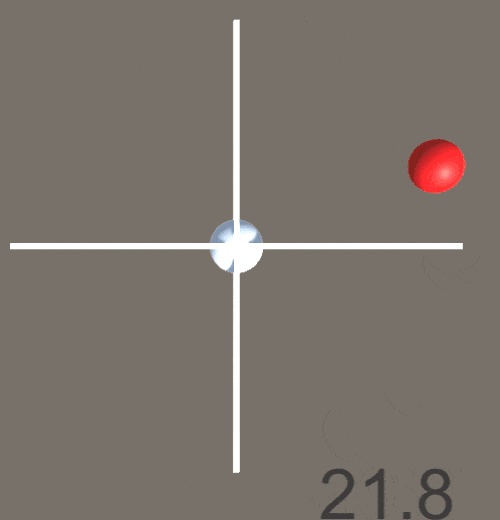
結果が以下のようになった。-180~180°の範囲で出力が得られていることがわかる。
Atan2関数の仕様を見てみる
UnityEngine.Mathf.Atan2の公式ドキュメント...は説明が十分ではないので、System.Math.Atan2の公式ドキュメントを見てみる。(基本的には同じはずなので)
以下のように条件分岐して戻り値が得られることが書かれている。
- 第一象限では$0<\theta<\pi/2$
- 第二象限では$\pi/2<\theta<\pi$
- 第三象限では$-\pi<\theta<-\pi/2$
- 第四象限では$-\pi/2<\theta<0$
単純な$tan^{-1}$から得られる角度が以上の法則で補正されて返ってくるらしい。
これを自力で実装するのは少し面倒なので関数として用意されていることはありがたい。調べてみると様々な言語でも似たようなAtan2関数が用意されていた。
例えばpythonでnumpyにおいてはnumpy.arctan2(ドキュメント)といった関数がある。
参考
【Unity】二次元ベクトルから角度を求めたり、角度から二次元ベクトルを求める処理|うにてぃブログ https://hacchi-man.hatenablog.com/entry/2020/03/05/220000
他
以下の様にVector3.Angleと内積を用いて計算する方法もあった。今回の目的であればAtan2関数を用いるのが手っ取り早いと思うが、これの場合は比較する軸方向に依存した処理にならないのでこちらを使いたい場面もあった。
2ベクトルの成す角度を時計回りで計算する|Yucchiy's Note https://blog.yucchiy.com/2020/10/calculating-angle/