まえがき
過去記事
あるネットワークが持つ『意識』の度合いをΦという値に計算して定量化する、統合情報理論というものがあります。
統合情報理論を扱うライブラリPyPhiの公式ドキュメントなどを参考にしつつ、Φの計算方法を見ていきます。
かなりややこしい計算になるので、色々省略しながら説明します。参考元の記事を読みたい人は、
以上の記事を見てください。また、自分が書いた前の記事 二つの話も含まれます。
足りない知識で雑な和訳をしているだけなので、有識者の指摘があればありがたいです。
ちゃんと読みたい方は公式スライド資料Calculating φと見比べながら読むといいと思います。
ネットワークとTPM(遷移確率行列)
このようなOR, AND, XORの三つの要素から構成されたネットワークを考えます。
A, B, Cそれぞれの要素は時間$t$においてON, OFFのどちらかの要素を持ち、また接続している要素に対して入出力を行います。その結果によって時間$t+1$における状態が変化します。
OR, AND, XORで構成されていることから、時間$t$の状態を行方向、時間$t+1$の状態を列方向に取ると以下のような表を作ることができます。
| t | \ | t+1 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| A | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | |||
| B | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | |||
| C | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | |||
| A | B | C | ↑ | ↑ | ↑ | ↑ | ↑ | ↑ | ↑ | ↑ | |
| 0 | 0 | 0 | → | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | → | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | → | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | → | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | → | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | → | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | → | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 1 | → | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
この表は、例えば$t$で$(0, 1, 1)$なら$t+1$の時$(1, 0, 1)$になる確率は$1$です。
この表をTPM(遷移確率行列)といいます。
Effect repertoires(効果レパートリー?)
A,B,Cの三つの要素から、「Aだけを取り出したもの」「ABだけを取り出したもの」「BCだけを取り出したもの」などの様々な組み合わせについて考えてみます。
ここから行う計算の前提として、$(A, B, C) = (1, 0, 0)$に固定したとします。
まず、「$t$の状態$(A, B, C)$に対する$t+1$における$(B, C)$」について調べてみましょう。
先ほどの表から、$t+1$におけるAの情報を削減すると、以下のような表を書くことができます。
|t| \ |t+1|||| ||
|---- | ----|---- |----| ----|---- | ----|---- |----| ----|---- | ----|
|| ||B|0|1|0| 1|
|| ||C|0| 0|1|1|
| A | B | C || | | | | | | | |
| 0 | 0 | 0 || 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 || 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 || 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 || 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 || 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 || 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 1 | 1 || 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 1 || 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
特に、$(A, B, C) = (1, 0, 0)$の時は
| B | 0 | 1 | 0 | 1 |
| C | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 |
$(B, C)=(0, 1)$になる確率が1であることがわかります。
同様に「$t$での状態$(C)$に対する$t+1$における$(B, C)$」を見てみると
|| |||||
|---- | ----|---- |----| ----|----|
||B|0|1|0| 1|
|| C|0| 0|1|1|
| C || | | | | | | | |
| 0 || 1/2 | 0 | 1/2 | 0 | 0 | 0 | 0 | 0 |
| 1 || 1/4 | 1/4 | 1/4 | 1/4 | 1 | 0 | 0 | 0 |
こんな風になります。
特に現在固定している$(1, 0, 0)$において
| B | 0 | 1 | 0 | 1 |
| C | 0 | 0 | 1 | 1 |
| 1/2 | 0 | 1/2 | 0 |
という表が作られます。
さらに「$t$での状態$(\varnothing)$(どれにも依存しない)に対する$t+1$における$(A)$」の表を作ってみましょう。
| A | 0 | 1 |
| 1/4 | 3/4 |
このように作ったこれらの表をeffect repertoire(効果レパートリー?)といいます。
先ほど作った表同士を掛け合わせることで、全体のeffect repertoireを計算することもできます。

$=$
||| ||||||
|---- | ----|---- |----| ----|---- | ----|---- |----| ----|
|A|0|1|0 |1|0| 1|0|1|
|B|0|0| 1|1|0| 0|1|1|
|C|0|0| 0|0|1| 1|1|1|
||||||||||
| | 1/8 | 3/8 | 0 | 0 | 1/8 | 3/8 | 0 | 0 | 0 | 0 |
Cause repertoire(原因レパートリー?)
先ほどは$t$から$t+1$に与える影響であるEffect Repertoireを見ました。
次に$t-1$から$t$に与える影響を見てみましょう。
「$t$での状態$(C)$に対する$t-1$における$(B, C)$」を見てみましょう。
||||||
|---- | ----|---- |----| ----|---- | ----|---- |----| ----|---- | ----|
| ||C|0| 1|
| B | C | || |
| 0 | 0 | | 1/2 | 1/2 |
| 1 | 0 | | 1/2 | 1/2 |
| 0 | 1 | | 1/2 | 1/2 |
| 1 | 1 | | 1/2 | 1/2 |
特に、今回固定する状態$(1, 0, 0)$においては
|||||
|---- | ----|---- |----| ----|---- | ----|---- |----| ----|---- |
| B | C | || |
| 0 | 0 | | 1/4 |
| 1 | 0 | | 1/4 || 0 | 1 | | 1/2 | 1/2 |
| 0 | 1 | | 1/4 | 1/2 |
| 1 | 1 | | 1/4 | 1/2 |
と求まります。(標準化して合計を1にしてあります)
これは$C$が0になるための$B, C$はどの状態も平等にありうる、ということを示します。
さらに「$t$での状態$(\varnothing)$(状態に依存しない)に対する$t-1$における$(A)$」を求めてみましょう。
| A | ||
| 0 | 1/2 | |
| 1 | 1/2 |
こうなりました。
先ほどと同様に、二つの表を掛け算してみましょう。
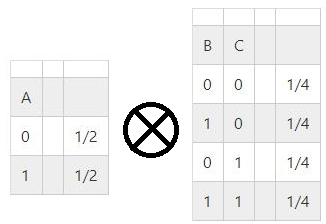
$ = $
|| ||||
|---- | ----|---- |----| ----|---- | ----|---- |
| A | B | C || | | | | ↑ | ↑ | ↑ | ↑ |
| 0 | 0 | 0 || 1/8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 || 1/8 | 0 | 1 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 || 1/8 | 0 | 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 || 1/8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 || 1/8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 || 1/8 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 1 | 1 || 1/8 | 0 | 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 1 || 1/8 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
こんな風に計算ができました。
irreducibility(削減不可能性?)
先ほどまでと同様に、$(A, C)$に対する$(A, B, C)$のEffect Repertoireを見てみましょう。
| A | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | ||
| B | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | ||
| C | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | ||
| A | C | |||||||||
| 1 | 0 | 1/4 | 1/4 | 0 | 0 | 1/4 | 1/4 | 0 | 0 |
このrepertoireを
$$ {AC\over ABC} $$
と表します。これを分解して、
$$ {AC\over AB} \times {\varnothing \over C} $$
という形にしてみましょう。
まず、$(A, C)$に対する$(A,B)$を見てみます。
| A | 0 | 1 | 0 | 1 | ||
| B | 0 | 0 | 1 | 1 | ||
| A | C | |||||
| 1 | 0 | 1/2 | 1/2 | 0 | 0 |
さらに、$\varnothing$(指定なし)に対する$C$を見てみます。
| ||||
| ----|---- |----| ----|---- | ----|---- |
|C|0|1|0 |1|0| 1|0|1|
| | || | | | | | | | |
| | | 1/2 | 1/2 | 1/2 | 0 | 0 | 1/4 | 1/4 | 0 | 0 |
$(A, C)$に対する$(A,B)$、$\varnothing$(指定なし)に対する$C$、この二つの表を掛けたものは、$(A, C)$に対する$(A, B, C)$の表に一致します。
$$ {AC\over ABC} と {AC\over AB} \times {\varnothing \over C} が一致する。$$
このように分割する組み合わせの取り方はたくさんあります。以下に列挙してみましょう。
$$ {\varnothing \over A}\times {AC\over BC}, {\varnothing \over B}\times {AC\over AC}, {\varnothing \over C}\times {AC\over AB} $$
$$ {\varnothing \over AB}\times {AC\over C}, {\varnothing \over BC}\times {AC\over A}, {\varnothing \over AC}\times {AC\over B} $$
$$ {\varnothing \over ABC}\times {AC\over \varnothing}, {A \over \varnothing}\times {C\over ABC}, {A \over A}\times {C\over BC} $$
$$ {A \over B}\times {C\over AC}, {A \over AB}\times {C\over C}, {A \over C}\times {C\over BC} $$
$$ {A \over BC}\times {C\over A}, {A \over ABC}\times {C\over \varnothing}$$
このすべての区切りについてcause repertoireを求め、大元である${AC\over ABC}$との比較を行います。
最も元の値とのズレが小さくなる区切りをMIP(minimum information partition、最小情報分割)、その時のズレを$φ$(小文字、スモールファイ)として評価します。この場合は$${AC\over AB} \times {\varnothing \over C} $$という区切りで$φ=0$となり、これがMIPとなります。
Maximally-irreducible cause-effect repertoire(最大に削減不能な因果レパートリー)
$$ABC\over ABC$$
から、様々なpurview(範囲)の$φ$をEffect repertoireから計算してみましょう。
$ ABC\over A $のMIPは${A\over \varnothing}\times {BC\over A}$で、$φ=0$。
$ ABC\over B $のMIPは${A\over \varnothing}\times {BC\over B}$で、$φ=0$。
$ ABC\over C $のMIPは${C\over \varnothing}\times {AB\over C}$で、$φ=0$。
$ ABC\over AB $のMIPは${A\over \varnothing}\times {BC\over AB}$で、$φ=0.5$。
$ ABC\over AC $のMIPは${\varnothing \over C}\times {ABC\over A}$で、$φ=0$。
$ ABC\over BC $のMIPは${AB\over C}\times {C\over B}$で、$φ=0.25$。
このうち$ ABC\over AB $の時が最も高い$φ_\mathrm{effect}^{\mathrm{max} }$を持つことになります。これをMaximally-irreducible effect repertoire(最大に削減不能な原因レパートリー?)と呼びます。
同様の計算を行うことcause-repertoireに関しても$φ_\mathrm{cause}^{\mathrm{max} }$を求めることができます。
$φ_\mathrm{cause}^{\mathrm{max} }$ ,
$φ_\mathrm{effect}^{\mathrm{max} }$
の二つから小さい方を採用してpurview(範囲)$ABC$の$φ$とします。
この計算を、$A, B, C, AB, BC, ABC$に関して計算してみます。
||A|B|C|AB|BC|ABC|
|----|----|----|----|----|----|----|----|
|$φ_\mathrm{cause}^{\mathrm{max} }$|0.17|0.17|0.50|0.25|0.33|0.50|
|$φ_\mathrm{effect}^{\mathrm{max} }$|0.25|0.25|0.25|0.50|0.50|0.50|
|$φ$|0.17|0.17|0.25|0.25|0.33|0.50|
System Cuts(構造の切断)
それぞれの部分構造がどれだけirreducible(削減不能であるか)をここまで計算してきました。
しかし、システム全体としてはどのように考えればいいのでしょうか?
ここでcut(切断)という概念を導入しましょう。
OR回路でできている「要素A」から「出る」経路を切断します。
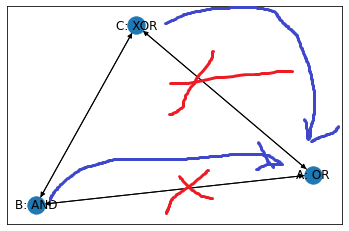
これで$A$の値が外部に影響を与えることはなくなりました。この時Aの値を「0」と扱うのではなく、「ノイズ」として扱うことに注意します。B, C「から」Aに接続する経路は生きていることにも注意。
まずは($A, B, C$)から($A$)へのTPMを見てみましょう。これは今まで通り、普通のOR回路。
|||||||
|----|---- | ----|---- |----| ----|---- | ----|---- |----| ----|---- | ----|
| |||A(OR)|0| 1|
|A| B | C | || |
|0| 0 | 0 | | 1 | 0 |
|1| 0 | 0 | | 1 | 0 |
|0| 1 | 0 | | 0 | 1 |
|1| 1 | 0 | | 0 | 1 |
|0| 0 | 1 | | 0 | 1 |
|1| 0 | 1 | | 0 | 1 |
|0| 1 | 1 | | 0 | 1 |
|1| 1 | 1 | | 0 | 1 |
次に($A, B, C$)から($B$)へのTPMを見てみましょう。BはAND回路ですが、Aの値が「ノイズ」であり、Bにとってはランダムな値になることで変化が起きます。
|||||||
|----|---- | ----|---- |----| ----|---- | ----|---- |----| ----|---- | ----|
| |||B(AND)|0| 1|
|A| B | C | || |
|0| 0 | 0 | | 1 | 0 |
|1| 0 | 0 | | 1 | 0 |
|0| 1 | 0 | | 1 | 0 |
|1| 1 | 0 | | 1 | 0 |
|0| 0 | 1 | | 1/2 | 1/2 |
|1| 0 | 1 | | 1/2 | 1/2 |
|0| 1 | 1 | | 1/2 | 1/2 |
|1| 1 | 1 | | 1/2 | 1/2 |
$(A, C)$の値が$(0, 1)$であるか$(1, 1)$であるか、経路が切断されているためBは判断することができません。よって1/2の確率で値が変化する形になりました。
同様にCについて求めます。
|||||||
|----|---- | ----|---- |----| ----|---- | ----|---- |----| ----|---- | ----|
| |||C(XOR)|0| 1|
|A| B | C | || |
|0| 0 | 0 | | 1/2 | 1/2 |
|1| 0 | 0 | | 1/2 | 1/2 |
|0| 1 | 0 | | 1/2 | 1/2 |
|1| 1 | 0 | | 1/2 | 1/2 |
|0| 0 | 1 | | 1/2 | 1/2 |
|1| 0 | 1 | | 1/2 | 1/2 |
|0| 1 | 1 | | 1/2 | 1/2 |
|1| 1 | 1 | | 1/2 | 1/2 |
XORなので、Aの値が決まってくれないと判断がつきません。
さて、ここまでで求めた三つの表を掛け合わせてみましょう。
| t | \ | t+1 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| A | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | |||
| B | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | |||
| C | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | |||
| A | B | C | |||||||||
| 0 | 0 | 0 | 1/2 | 0 | 0 | 0 | 1/2 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 1/2 | 0 | 0 | 0 | 1/2 | 0 | 0 | 0 | |
| 0 | 1 | 0 | 0 | 1/2 | 0 | 0 | 0 | 1/2 | 0 | 0 | |
| 1 | 1 | 0 | 0 | 1/2 | 0 | 0 | 0 | 1/2 | 0 | 0 | |
| 0 | 0 | 1 | 0 | 1/4 | 0 | 1/4 | 0 | 1/4 | 0 | 1/4 | |
| 1 | 0 | 1 | 0 | 1/4 | 0 | 1/4 | 0 | 1/4 | 0 | 1/4 | |
| 0 | 1 | 1 | 0 | 1/4 | 0 | 1/4 | 0 | 1/4 | 0 | 1/4 | |
| 1 | 1 | 1 | 0 | 1/4 | 0 | 1/4 | 0 | 1/4 | 0 | 1/4 |
これが「AからB, Cへの経路を切断したTPM」です。
このように切断したネットワークが切断していないネットワークのTPMと比べてどう変化したか、というのが大切になります。
big-Phiを計算してみよう
このTPMを元に再びMaximally-irreducible cause-effect repertoireを計算してみます。
先ほど計算した範囲を再び計算してみる...と...
$B$に関するMaximally-irreducible cause-effect repertoireのみが変化しました。切断した場合、切断していない場合でcause-effectそれぞれのTPMの誤差を計算すると、$0.17$の違いがありました。
さらにこれだけでは終わりません。Maximally-irreducible cause-effect repertoireが変化しなかった残りの範囲$A, C, AB, BC, ABC$は、切断をした際の範囲$\varnothing$(指定なし)でのTPMとの比較を行います。それぞれの値に$0.583, 1, 1, 1.25, 2$の差が生じました。
これらの差を、それぞれの範囲の持つ$φ$の値と掛け算して合計します。
||A|B|C|AB|BC|ABC|
|----|----|----|----|----|----|----|----|
|自身とのTPMの差|0|0.17|0|0|0|0|
|範囲$\varnothing$とのTPMの差|0.583||1|1|1.25|2|
|$φ$|0.17|0.17|0.50|0.25|0.33|0.50|
|差(どちらか)と$φ$を掛けた値|0.097|0.289|0.25|0.25|0.4125|1|
表の最後の列を合計すると$=2.0416$となります。これが integrated conceptual information(統合概念情報?)、$Φ$(ラージファイ)と呼ばれる値です。
これは「Aから出る経路」を切断した際の値ですが、「Bから出る経路」「Cから出る経路」「ABから出る経路」「BCから出る経路」「ACから出る経路」それぞれを切断した場合も別々に$Φ$を計算します。
それぞれ計算した値を表にしました。
|切断する経路元|A|BC|B|AC|C|AB|
|----|----|----|----|----|----|----|----|
|$Φ$|2.042|1.924|2.042|1.924|1.972|1.917|
これらの値から一番$Φ$が小さくなる値を系全体の$Φ$、またこの時の区切りをMIP(minimum
information partition)と呼びます。この場合はABを元に切断するのがMIPになるようです。
よって$ABC$の情報統合能力を示す値は$Φ=1.917$と求まりました。
ライブラリで計算してみよう
この値を、pyphiというライブラリで計算してみます。前書いた記事のコードを張り付けているだけなので、コード面の解説は(少しだけですが)そっちを見てください。
まずTPMを記述して(フォーマットが異なる書き方をしていますが内容は同じです)、ネットワークの接続を記述して、pyphi.Network()クラスを作成して...
import pyphi
import numpy as np
tpm = np.array([
[0, 0, 0],
[0, 0, 1],
[1, 0, 1],
[1, 0, 0],
[1, 0, 0],
[1, 1, 1],
[1, 0, 1],
[1, 1, 0]
])
cm = np.array([
[0, 1, 1],
[1, 0, 1],
[1, 1, 0]
])
labels = ('A', 'B', 'C')
# この場合のcmは省略可能
network = pyphi.Network(tpm, cm=cm, node_labels=labels)
ABCの初期状態(1, 0, 0)を設定して...
state = (1, 0, 0)
計算対象を設定して...
subsystem = pyphi.Subsystem(network, state)
計算します。
pyphi.compute.phi(subsystem)
# 1.916665
同様の結果が得られました。
参考元
基本的に以下の記事の内容に沿って和訳したものです。もうちょっとちゃんと見たい方はこちらから読んでください。この記事は飛ばしてる概念が多すぎます。
pyphiの公式ドキュメントは以下↓です。
指摘する点があればしていただければとてもありがたいです。記事が長文になりすぎて地獄でした。元のスライド資料200ページ越えはやばかった。
